CO-ORDINATE GEOMETRY in the (X,Y) PLANE

C4 Chapter 2

CO-ORDINATE GEOMETRY IN THE (x,y) PLANE

PARAMETRIC EQUATIONS

Coordinates x and y are expressed as functions of a parameter. x = f(t) and y = g(t)

Example

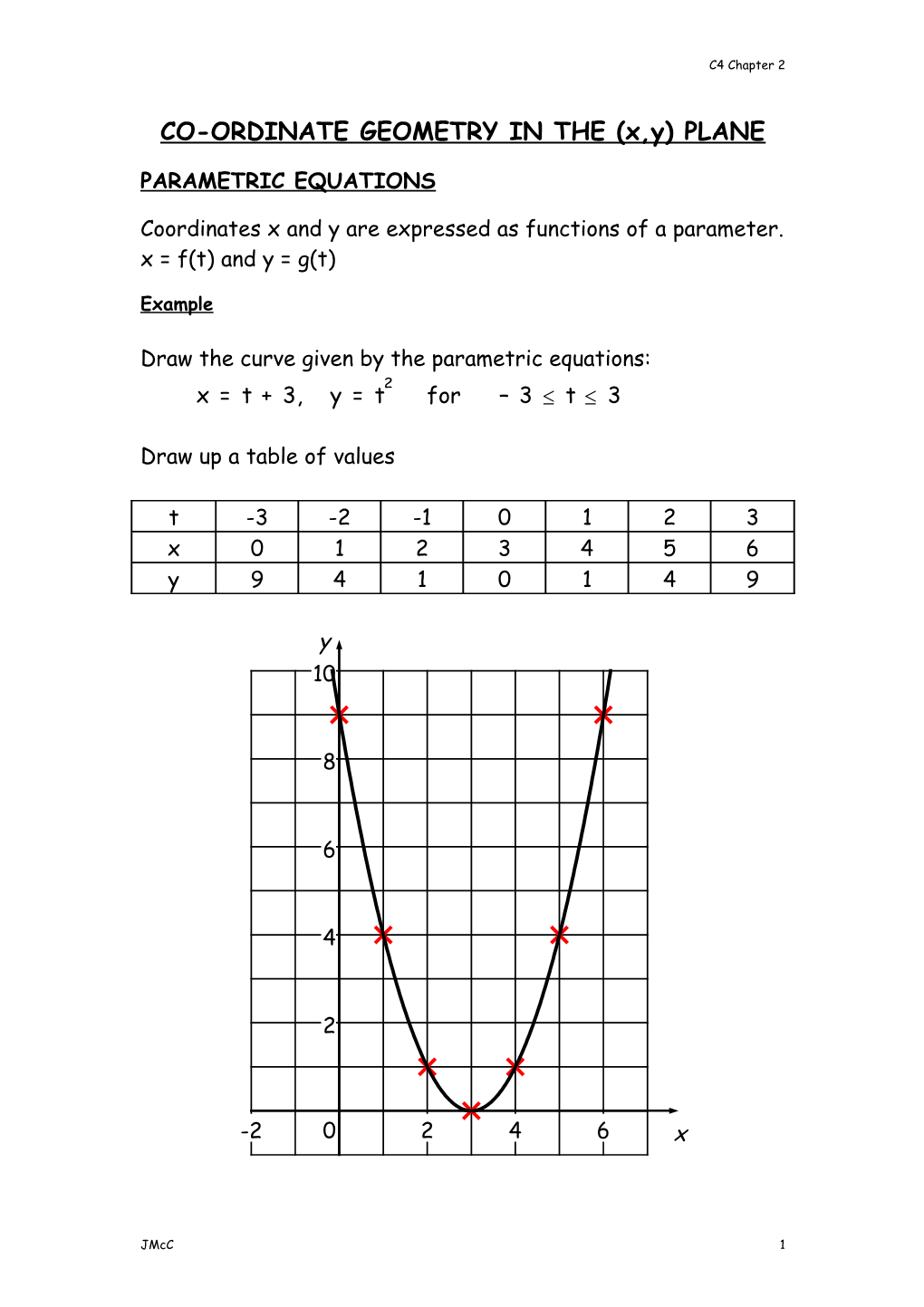
Draw the curve given by the parametric equations: 2 x = t + 3, y = t for – 3 £ t £ 3

Draw up a table of values

t -3 -2 -1 0 1 2 3 x 0 1 2 3 4 5 6 y 9 4 1 0 1 4 9

-2 0 2 4 6 x

JMcC 1

2 x = t + 3, y = t for – 3 £ t £ 3 C4 Chapter 2

To find the Cartesian equation of the curve, you need to eliminate the parameter between the two equations

Example 1

Find the Cartesian equation of the curve given by the parametric equations: 2 x = t + 3, y = t

Make t the subject Þ t = x – 3

2 Substitute into the y equation Þ y = (x – 3)

Check: this is the parabola y = x2 translated 3 units to the right (see previous example)

Example 2

Find the Cartesian equation of the curve given by the parametric equations: 1 2 x = , y = , t ¹ – 3, t ¹ 5 t + 3 t – 5

Make t the subject: 1 1 1 1 – 3x x = Þ t + 3 = Þ t = – 3 = t + 3 x x x Substitute into the y equation:

1 – 3x 1 – 8x t – 5 = – 5 = x x 1 – 8x 2x \ y = 2 ¸ Þ y = x 1 – 8x

Ex 2A p 10

JMcC 2

2 x = t + 3, y = t

2 SMuabkset itt utthee insutob jtehcet yÞ eqtua=tioxn–Þ3 y = (x – 3)

1 2 x = , y = , t ¹ – 3, t ¹ 5 t + 3 t – 5

MSuabkset itt1 utt1hee – isn13utobx– jte8hcext :y eq11ua–tio8nx2: x 1 1 – 3x xt\ –=y5= =2 ¸Þ t +–35Þ== y Þ= t = – 3 = t + 3 x x x x1 – 8xx x C4 Chapter 2

USING PARAMETRIC EQUATIONS TO SOLVE PROBLEMS

Example 1

Find the coordinates of the point where the curve with parametric equations: x = √t, y = 4t – 25 meets the x-axis

25 At the x – axis, y = 0 Þ 4t – 25 = 0 Þ t = 4

25 5 \x = t = ± = ± 4 2

æ 5 ö æ 5 ö Points of intersection are ç , 0 ÷ and ç – , 0 ÷ è 2 ø è 2 ø

Example 2

Find the coordinates of the points of intersection of the curve with parametric equations: x = 2t, y = t2 and the straight line y = x + 3

Substitute the parameters into the equation of the line:

2 2 t = 2t + 3 Þ t – 2t – 3 = 0 \ (t – 3)(t + 1) = 0 Þ t = 3, – 1

\ when t = 3 Þ x = 6 and y = 9

\ when t = – 1 Þ x = – 2 and y = 1

Points of intersection are (6, 9) and ( – 2, 1)

Ex 2B p 13

JMcC 3

25 5 25 \Atx th=e xt –=a±x is, y = =0 ± Þ 4t – 25 = 0 Þ t = æ 5 ö æ 45 ö Points of intersec4tion are2 ç , 0 ÷ and ç – , 0 ÷ è 2 ø è 2 ø

2 2 tSP\ou i(wb=ntsths2t–ei tnou3 f+t) e(int=3 the+3Þer–1s Þp)e1tac=rÞtxai–o0mn=2xe Þtat6=re –er t s3a – (=ni6n2d=t,3 o 9,0 ya)t h–n e= da1 en 9 qdy u a= (tio1– n 2o,f 1 t) he line: C4 Chapter 2

PARAMETRIC EQUATIONS INVOLVING TRIGONOMETRIC PARAMETERS

You will need to use some of the Trigonometric Identities from C3

Example 1

Find the Cartesian equation of the curve given by: x = cos t, y = sin 2t y = sin 2t = 2 sin t cos t = 2x sin t \ we need to find sin t in terms of x or y

2 2 2 2 sin t = 1 – cos t Þ sin t = 1 – cos t = 1 – x

2 \y = 2x 1 – x

Example 2

Find the Cartesian equation of the curve given by: x = sec t, y = 4 sin t

1 1 y = 4 sin t and x = sec t = Þ cos t = cos t x

2 2 2 2 x – 1 (x – 1) sin t = 1 – cos t = 1 – (1 ¸ x ) = 2 = x x

2 4 (x – 1) \ y = x

Ex 2C p 15

JMcC 4

2 22 2 2 s\yiny =wt=es =in2 e1x2etd–1 =tc–oo2 sxf sitn indÞ ts icnso itns itn =ter2m1xs –s oincf o txs otr= y 1 – x

2 1 2 1 2 y = 4 sin4 t ( x an–d2 1 )x = sec t = 2 Þ cxos– t1= (x – 1) s\in ty== 1 – cos t = 1 – (1 ¸ x ) = 2 = x cos t x x x C4 Chapter 2

AREA UNDER A CURVE GIVEN BY PARAMETRIC EQUATIONS

dx Since Area = y dx, Chain Rule Þ y dx = y dt ò ò ò dt

Example

The diagram shows the curve with parametric equations: 2 x = t , y = t(5 – t) The region R is bounded by the curve and the x-axis. Find the area of R.

0 5 10 15 20 25 x

Curve crosses x – axis at (25, 0) Þ t(5 – t) = 0 Þ t = 5 25 5 dx 5 Area = y dx = y dt = t(5 – t) ´ 2t dt ò0 ò0 dt ò0

5 3 4 5 2 3 é 10t 2t ù = (10t – 2t ) dt = ê – ú = 104·17 ò0 ë 3 4 û o

Ex 2D p 18 & Mixed Ex 2E p 19

JMcC 5

dx Since Area = 2 y dx, Chain Rule Þ y dx = y dt x =òt , y = t(5 – t) ò ò dt

Curve cros25ses x – axis5 at (d2x5, 0) Þ 5t(5 – t) = 0 Þ t = 5 Area5= y dx = y dt3 = 4 t(55 – t) ´ 2t dt 2 3 é ù ò0 ò0 dt10t ò20t = (10t – 2t ) dt = ê – ú = 104·17 ò0 ë 3 4 û o