Math Study Guide 2014

You have learned A LOT this year! This study guide will help you remember what we did so you can be ready for the test on ______!

1. Graphing 3.17 The student will a) collect and organize data, using observations, measurements, surveys, or experiments; b) construct a line plot, a picture graph, or a bar graph to represent the data; and c) read and interpret the data represented in line plots, bar graphs, and picture graphs and write a sentence analyzing the data.

Linguistic Complexity Language Forms and Conventions What kind of graph is this? How can you tell? This is a ____ graph because How many more=subtract ____. Which ____ was liked the most/least? How many more…? What does survey-surveys the key tell us? What data does this graph show?

How many students liked grape juice? ______

How many more studnets liked apple juice than orange juice? ______

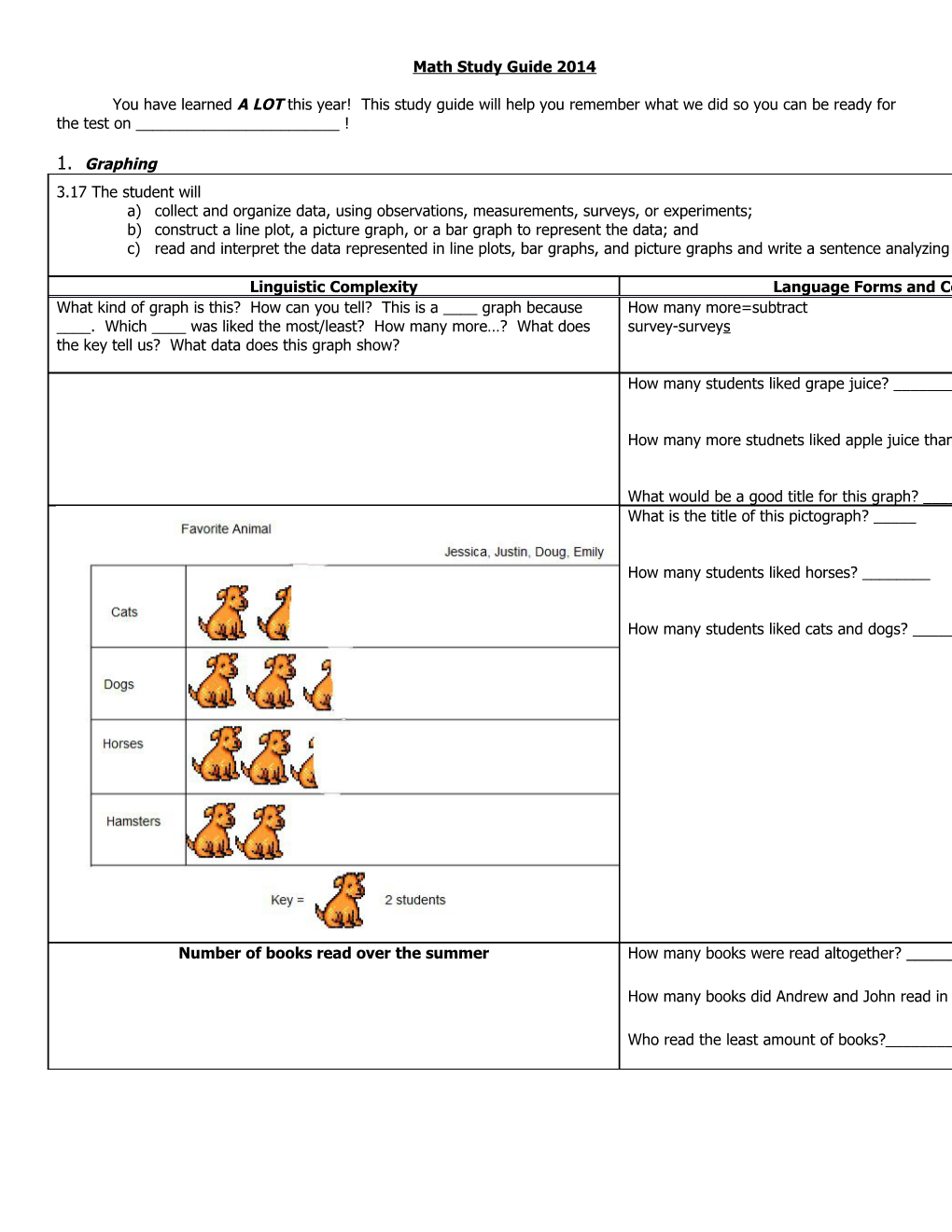
What would be a good title for this graph? ______What is the title of this pictograph? _____

How many students liked horses? ______

How many students liked cats and dogs? ______

Number of books read over the summer How many books were read altogether? ______

How many books did Andrew and John read in total? ______

Who read the least amount of books?______

Favorite City How many people voted for Sydney? ______

How many fewer people chose Sydney than Paris? ______Hours spent swimming Complete the frequency chart.

How many people spent 4 hours swimming? ______

How many people swam either two hours or five hours? ______

Using the data from the question above, create a line plot, bar graph, and pictograph. 2. Place Value 3.1 The student will a) read and write six-digit numerals and identify the place value and value of each digit

Linguistic Complexity Language Forms and Conventions Vocabulary What digit is in the ____ place? ___ is expand-expanded Digit, Place value, Number, Numeral, in the ___ place. one-ones Standard form, Expanded form What is the value of the digit in the ___ ten-tens place? The value is ____.

Here are ALL the place value places you know!  That’s a lot! 

Write what the 9 represents in the Write a number with a 9 in the Find the digit in the thousands numeral: hundreds place. place in the numeral: 394,819? 284,098 673 or 600 or 699…lots of right 4,000 4 answers! Write a number that has a 2 in the thousands place. Write a number that has a 9 in the tens place. In the number 852,929 what place is the 8 in? In the number 40,751 what is the value of the 7? Circle the 3 numbers that have a 4 in the ten 1,841 43,181 408,127 64,087 340,167 197,194 10,401 948,054 thousands place Standard Form Expanded Word form Seven thousand, two hundred ninety 7,293 7,000+200+90+3 three Use the number 6,529 to complete the boxes below:

Standard form Expanded Word form 3. Rounding 3.1 The student will b) round whole numbers, 9,999 or less, to the nearest ten, hundred, and thousand; and

Linguistic Complexity Language Forms and Conventions Vocabulary What would ___ round to? ___ round-rounds-rounded-rounding Rounding, Estimation rounds to ___ because ____.

Round 768 to the nearest Round 768 to the nearest Round 768 to the nearest ten hundred thousand 770 800 1,000 Round to the nearest ten Round to the nearest hundred Round to the nearest thousand

532 = ______532 = ______532 = ______

Circle all the numbers that can be rounded to 1,000 1,293 2,202 1,939 1,429 1,743 553

Write a number that would round to 250

To the nearest hundreds, how many pounds of candy were sold in February?

To the nearest tens, how many pounds of candy Use this table to answer the questions to the right: were sold in October?

Pounds of Candy Sold October 6,812 February 3,157 April 4,878 To the nearest thousands, how many pounds of candy were sold in April? 4. Comparing Numbers 3.1 The student will c) Compare two whole numbers between 0 and 9,999, using symbols (>, <, or = ) and words (greater than, less than, or equal to).

Linguistic Complexity Language Forms and Conventions Vocabulary ____ is greater than/ less than/ equal Greater than, Less than, Equal to, to ____. Compare

Use the symbols (>,<,=) to make the following Use a phrase (greater than, less than, equal to) to true: make the following true: 1,892 ? 2,128 826 ? 928

826 < 928 1,892 is less than 2,128

Use the symbols (>,<,=) to make the following Use a phrase (greater than, less than, equal to) to true: make the following true:

763 ? 349 2,081 ? 5,142

Circle all the statements that are true. 724 < 923 682 > 689 745 < 682 7,593 < 7,823 563 = 563 752 > 578 8,483 is greater than 5,293 7,382 is less than 8,833 182 is greater than 56

5. Fact Families 3.2 The student will recognize and use the inverse relationships between addition/subtraction and multiplication/division to complete basic fact sentences. The student will use these relationships to solve problems. Linguistic Complexity Language Forms and Conventions Vocabulary Which of the following number relate-related-relative Inverse relationship, Factor, Number sentences is related to the fact ____? sentence, Related facts ___ is related because ___. Which of the following number sentences does not belong in a fact family with __,__, and ___? ___ does not belong because ____.

Write the fact family for 8, 3, and 11 Which of these ‘facts’ is wrong? 8 + 3 = 11 11 – 8 = 3 12 + 7 = 19 19 + 7 = 12 3 + 8 = 11 11 – 3 = 8 7 + 12 = 19 19 – 12 = 7 Write the fact family for 4, 12, and 16 Which of these ‘facts’ is wrong? 2 + 13 = 15 13 + 2 = 15 13 – 2 = 15 15 – 2 = 13 Write the other number sentences related to 8 + 2 Fill in the blank with the correct number. =10 If 13 -3 = 10, then 10 + ____ = 13 If 10 + 6 = 16, then 16 = 10 - ____ 11 + 4 = 15, then 15 – 11= ___s

6. Addition 3.4 The student will estimate solutions to and solve single-step and multistep problems involving the sum of two whole numbers, each 9,999 or less, with or without regrouping.

Linguistic Complexity Language Forms and Conventions Vocabulary How do you know? add-addend-addition Addend, Sum

1 1 1 1 1 1 1 5, 1 6 8 8, 3 7 9 5 1 6 8 8 3 7 9 + 8 2 2 + 1 4 5 + 8 2 2 + 6 2 5

5, 9 9 0 8, 5 2 4 5, 9 9 0 9, 0 0 4 f

9 3 3 , 4 6 2 , 2 6 1 9, 4 6 2 , 2 6 1

+ 7 5 1 + 4 1 3 + 7 5 1 + 4 1 3

7. Addition Properties 3.20 The student will a) investigate the identity and the commutative properties for addition; and b) identify examples of the identity and commutative properties for addition.

Linguistic Complexity Language Forms and Conventions Vocabulary Which of the following shows the add-addend-addition Property, Identity, Identity property, identity/ commutative property? Commutative property, Equal

Communtative Property Identity Property This is an order property. Changing the order of the When the number zero is added to another number or addends does not change the sum. another number is added to the number zero, that number remains unchanged. 3 + 2 = 5 and 2 + 3 = 5 5 + 0 = 5 and 0 +105 = 105

Write an example of the communtative property. Write an example of the identity property

Circle all the examples of the communtative Circle all the examples of the Identity property. property. 5 + 3 = 8 and 3 + 5 = 8 4 + 0 = 4 16 + 0 = 16 6 + 4 = 10 and 5 + 5 = 10 9 + 1 =10 nad 1 + 9 =10 0 +0 = 0 15 + 1 = 16 8. Subtraction 3.4 The student will estimate solutions to and solve single-step and multistep problems involving the difference of two whole numbers, each 9,999 or less, with or without regrouping.

Linguistic Complexity Language Forms and Conventions Is ___ a good estimate for this problem? ___ is/is not a good estimate because subtract-subtraction ____. estimate-estimation group-regroup What is the difference between ___ and ___? The difference is ___.

1 1 1 1 4 1 2 9 0 4 1 5 1 7 9 9 10 5, 1 6 8 3 0 0 5 1 6 1 8 0 0 0 - 8 2 2 - 1 4 5 - 8 2 8 - 6 2 2

4, 3 4 4 1 5 5 4, 3 3 7, 3 7 8

9 , 0 0 0 3, 2 6 1 7 0 0 6 0 5

- 5 5 5 - 4 1 3 - 4 5 1 + 4 9 3 9. Length and Perimeter 3.9 The student will estimate and use U.S. Customary and metric units to measure a) length to the nearest -inch, inch, foot, yard, centimeter, and meter; 3.10 The student will a) measure the distance around a polygon in order to determine perimeter; and

Linguistic Complexity Language Forms and Conventions Vocabulary What unit would you use to measure meter-centimeter Foot, Inch, Length, Measure, Yard, ___? Why? I would use ___ to long-length Centimeter, Meter, Distance, measure because ___. Which of the measure-measurement Perimeter, Ruler, Estimate, Polygon, following is a good estimate of the Square units, Surface perimeter? Perimeter – distance around the outside of an object Find the perimeter.

Perimeter: 4+6+5=15cm

Find the perimeter Find the perimeter.

You need to use a rule to find the length in inches and centimetters. Rulers are found at the last page of the study guide. Find the length using your centimeter ruler 10.Multiplication Strategies 3.5 The student will recall multiplication facts through the twelves table, and the corresponding division facts. 3.6 The student will represent multiplication, using area, set, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor 5 or less.

Linguistic Complexity Language Forms and Conventions Vocabulary What is the product of ___ and ___? factor-factors Factor The product is ___. Which of the multiply-multiplication Product following arrays shows the fact ___? Area This array shows ___ because ___. Multiply What is the area of this figure? The Array area is ___. Number Lines Models What does this picture show?

3 x 9 = 27 9 x 3 = 27 3 x 5 = 15

Repeated addition Arrays 3 x 4 =

3 6 9

+ 3 + 3 + 3 6 x 4 = 24 6 9 12

Make an array for 4 x 3 =

Show a model for 5 x 4 =

Show 4 x 3 on your own number line

Use repeated addition to solve 6 x 4 =

11.Division Strategies 3.6 The student will represent division, using area, set, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor 5 or less.

Linguistic Complexity Language Forms and Conventions Vocabulary What is the quotient of ___ divided by divide-division Equal ___? The quotient is ___. Which Quotient multiplication number sentence helps divide you solve this division problem? Models Arrays

27 ÷ 3 = 9

8 ÷ 2 = 4

Number Lines

27 ÷ 3 = 9

Show a model of 18 ÷ 6 = Make an array for 24 ÷ 3 =

Show 21 ÷ 7 = on your own number line 12.Fact Families: Multiplication and Division 3.2 The student will recognize and use the inverse relationships between multiplication/division to complete basic fact sentences. The student will use these relationships to solve problems. Linguistic Complexity Language Forms and Conventions Vocabulary Which of the following number relate-related-relative Inverse relationship, Factor, Number sentences is related to the fact ____? fact family - families sentence, Related Facts, Numeral, Fact ___ is related because ___. Which of multiply-multiplication family, Multiply, Product, Divide, the following number sentences does divide-division Dividend, Divisor, Quotient, Addend, not belong in a fact family with __,__, Sum, Identity property, Commutative and ___? ___ does not belong property because ____.because ____.

Write the fact family for 8, 3, and 24 Which of these ‘facts’ is wrong? 8 X 3 = 11 11 ÷ 8 = 3 5 x 7 = 35 7 ÷ 5 = 35 3 X 8 = 11 11 ÷ 3 = 8 7 x 5 = 35 35 ÷ 5 = 7 Write the fact family for 4, 12, and 3 Which of these ‘facts’ is wrong? 2 x 8 = 16 8 x 2 = 16 16 ÷ 2 = 8 2 ÷ 8 = 16 Write the other number sentences related to 8 X 2 Fill in the blank with the correct number. =16 If 5 x 3 = 15, then 15 ÷ ____ = 3 If 7 x 6 = 42, then 6 = 42 ÷ ____ 9 x 4 = 36, then 36 ÷ 9 = ___ 13. Multiplication Properties 3.20 The student will a) investigate the identity and the commutative properties for multiplication; and b) identify examples of the identity and commutative properties of multiplication.

Linguistic Complexity Language Forms and Conventions Vocabulary Which of the following shows the multiply-multiplication Identity property, Commutative identity/ commutative property? property

Communtative Property Identity Property This is an order property. Changing the order of the When the number one is multiplied by another number or factors does not change the product another number is multiplied by the number one, that number remains unchanged. 3 x 5 = 15 and 5 x 3 = 15 1 x 9 = 9 12 x 1 = 123

Write an example of the communtative property. Write an example of the identity property

Circle all the examples of the communtative Circle all the examples of the identity property. property.

7 x 2 = 2 x 7 3 x 6 = 2 x 9 8 x 3 = 8 x 2 1 x 3=3 4 x 4=16 7x1=1

4 x 5 = 5 x 4 6 x 2 = 2 x 6 8 x 1 = 1 + 8 0 x 8=0 8 x 1=8 12 x 2=24

7 x 3 = 3 x 7 5 x 4 = 10 x 2 3 x 9 = 9 x 3 1x6=6 2 x 2=4 0 x 3=0 13.Area 3.10 The student will b) count the number of square units needed to cover a given surface in order to determine area.

Linguistic Complexity Language Forms and Conventions Vocabulary Area – square units inside of an Find the area. Find the area. object

1 2 3 4 5 6

Area: 6 square units

14.Calendar 3.12 The student will identify equivalent periods of time, including relationships among days, months, and years, as well as minutes and hours.

Linguistic Complexity Language Forms and Conventions Vocabulary How many minutes/ hours/ days / a.m.=morning Days, Weeks, Months, Hours, Minutes weeks/ months are in a hour/ day / p.m.=afternoon/night week/ month/ year? hour-hours What time does this clock show? The time is ___. The hour/minute hand is showing ____. Key information:  7 days in a week (Sunday-Saturday) 12 months in a year (January-December)  365 days in a year (every 4 years there are 366 days due to leap year)  Certain months have 31 days (Jan, March, May, July, Aug, Oct, and Dec.)  Certain months have 30 days (April, June, Sept, Nov)  February has 28 days unless it is a leap year (every 4 years) and then it has 29

Circle all answers that are equal to 1 year. How many months would be in 3 years?

365 days 11 months 7 days 12 months 361 days 15.Money 3.8 The student will determine, by counting, the value of a collection of bills and coins whose total value is $5.00 or less, compare the value of the bills and coins, and make change.

Linguistic Complexity Language Forms and Conventions Vocabulary What is the total amount of money coin-coins Dollars, Cents, Change show? If __ buys ___ and pays with bill-bills coins ___, what will his change be? His dollar-dollars bills change will be ___. Know the amounts of each bill and coin.

Know how to add and subtract money (finding change) Pay – cost = change

Find the amount.

Find the amount. 4 quarters, 3 dimes = 1 quarter, 5 nickels, 3 pennies 2 dimes, 5 nickels, 1 penny = 3 quartrers, 3 nickels = Kasie goes into a store and buys 3 pieces of candy. One costs 85¢, one costs $1.65 and the last one costs $1.30. She gives the cashier $5.00. What is her change?

Chase goes into a toy store and buys 2 toys. They each cost $2.15. He gives the cashier $5.00. How much change will he receive? 16.fractions 3.3 The student will a) name and write fractions represented by a model; b) model fractions and write the fractions’ names; and Linguistic Complexity Language Forms and Conventions Vocabulary What fraction of the figure is shaded? numerator=top number Fraction, Numerator, Denominator, , What is the numerator / denominator? denominator=bottom number Whole number The numerator / denominator is ___. shade-shaded Pictures Words Numbers 5 Five sixths 6

1 One eighth 8

Pictures Words Numbers

One third

17.mixed numbers 3.3 The student will a) name and write fractions (including mixed numbers) represented by a model; b) model fractions (including mixed numbers) and write the fractions’ names; and Linguistic Complexity Language Forms and Conventions Vocabulary What fraction of the figure is shaded? numerator=top number Fraction, Numerator, Denominator, What is the numerator / denominator? denominator=bottom number Mixed number, Whole number The numerator / denominator is ___. mix-mixed Which fraction is greater/less than shade-shaded

3 ¼ What is the mixed number Shade in the model to create the mixed number 3 3/5

18. comparing fractions 3.3 The student will c) compare fractions having like and unlike denominators, using words and symbols (>, <, or =). Linguistic Complexity Language Forms and Conventions Vocabulary What fraction of the figure is shaded? numerator=top number Fraction, Numerator, Denominator, What is the numerator / denominator? denominator=bottom number Mixed number, Whole number, Greater The numerator / denominator is ___. mix-mixed than Less than Which fraction is greater/less than shade-shaded Which phrase (greater than, less than, or Which symbol (>, <, =) would you use equal to) would you use to compare the to compare the following fractions? following fractions?

Less than = Which phrase (greater than, less than, or equal to) would you use to compare the Which symbol (>, <, =) would you use following fractions? to compare the following fractions?

19. adding and subtracting fractions 3.7 The student will add and subtract proper fractions having like denominators of 12 or less.

Linguistic Complexity Language Forms and Conventions Vocabulary What fraction of the figure is shaded? numerator=top number Fraction, Numerator, Denominator, What is the numerator / denominator? denominator=bottom number Whole number The numerator / denominator is ___. mix-mixed Which fraction is greater/less than shade-shaded

1 3 4 2 1 1 + = - = 5 5 5 3 3 3

20. probability 3.18 The student will investigate and describe the concept of probability as chance and list possible results of a given situation.

Linguistic Complexity Language Forms and Conventions Vocabulary What is the probability of ___? The predict-prediction Possible outcome, Impossible event, probability is ___. What are all the possible-impossible Impossible, Unlikely, Predict, Equally, possible outcomes of___? The likely-unlikely Likely, Probability, Certain, Least likely, possible outcome are___. It is likely/ equal-equally Most likely, As likely as unlikely / certain / impossible for ___ because ___. words we use when talking about probability. • Impossible • Unlikely • Equally Likely • Likely • Certain • As likely as

Label each spinner with one of the 5 probability words. What are your chances of ♦ ?

What are your chances of spinning a ♣ ?

21. patterns 3.19 The student will recognize and describe a variety of patterns formed using numbers, tables, and pictures, and extend the patterns, using the same or different forms.

Linguistic Complexity Language Forms and Conventions Vocabulary What will come next in this pattern? repeat-repeating Patterns, Table, Rule, Growing, Why? ___ will come next in the pattern-patterns Repeating, Extending, Numeric pattern because ___. patterns, Geometric patterns, Multiples, Function What is the rule for this table? How can you tell? The rule is ___ because ___. You can add to a pattern, as well as figure out what the pattern is. 22. 2 digit by 1 digit multiplication 3.6 The student will represent multiplication and division, using area, set, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor 5 or less. Linguistic Complexity Language Forms and Conventions Vocabulary What is the product of ___ and ___? multiply-multiplication Multiply, Product, Factor The product is ___. product-products 3 3 x 57 = 2 2 9 5 7 x 4 Hmm…this is too hard written x 3 this way. 1 7 1 1 1 6 I’ll copy it over to make it easier!

5 x 68 = 3 4 x 9

23.Geometry 3.15 The student will identify and draw representations of points, line segments, rays, angles, and lines. Linguistic Complexity Language Forms and Conventions What are this properties of this shape? The properties are ___. How angle-rectangle-triangle many vertices/edges/faces does ___ have? ___ has ___ property-properties vertices/edges/faces. Are these figures congruent? Why or why not? rectangle-rectangular These figures are/are not congruent because ____. vertex-vertices congruent-noncongruent Line Ray Point Line Segment Angle

24.Geometry 3.16 The student will identify and describe congruent and noncongruent plane figures.

Linguistic Complexity Language Forms and Conventions Vocabulary What are this properties of this shape? angle-rectangle-triangle Square, Rectangle, Triangle, Circle, The properties are ___. How many property-properties Right angle, Opposite, Plane, vertices/edges/faces does ___ have? rectangle-rectangular Properties, Sphere, Cube, Rectangular ___ has ___ vertices/edges/faces. Are vertex-vertices prism, Square pyramid, Cone, these figures congruent? Why or why congruent-noncongruent Cylinder, Angle, Vertices, Edges, not? These figures are/are not Faces, Solid geometric figure, Point, congruent because ____. Line, Line segment, Ray, Endpoint, Vertex, Plane figures, Polygon, Sides, Size, Shape, Congruent, Congruency, Noncongruent Conguent/congruency means same shape and same size Are they congurent? Are they congurent?

No Draw conguent shapes

Draw a congruent shape:

25.geometry 3.14 The student will identify, describe, compare, and contrast characteristics of plane and solid geometric figures (circle, square, rectangle, triangle, cube, rectangular prism, square pyramid, sphere, cone, and cylinder) by identifying relevant characteristics, including the number of angles, vertices, and edges, and the number and shape of faces, using concrete models. Linguistic Complexity Language Forms and Conventions Vocabulary What are this properties of this shape? angle-rectangle-triangle Square, Rectangle, Triangle, Circle, The properties are ___. How many property-properties Right angle, Opposite, Plane, vertices/edges/faces does ___ have? rectangle-rectangular Properties, Sphere, Cube, Rectangular ___ has ___ vertices/edges/faces. Are vertex-vertices prism, Square pyramid, Cone, these figures congruent? Why or why congruent-noncongruent Cylinder, Angle, Vertices, Edges, not? These figures are/are not Faces, Solid geometric figure, Point, congruent because ____. Line, Line segment, Ray, Endpoint, Vertex, Plane figures, Polygon, Sides, Size, Shape, Congruent, Congruency, Noncongruent Shere Retangular prosm cone cube cylinder

26. weight/mass 3.9 The student will estimate and use U.S. Customary and metric units to measure c) weight/mass in ounces, pounds, grams, and kilograms; and

Linguistic Complexity Language Forms and Conventions Vocabulary Which unit would you use to measure measure-measurement weight, mass, ounce, pound, gram, ___? You would measure ___ using pound-pounds kilogram ___. Which is the best estimate for ___? Why weight ( grams, kilograms, ounces, pounds) How would you measure the weight of a How would you measure the weight of a rd bike? 3 grader?

In pounds

27. volume/capacity 3.9 The student will estimate and use U.S. Customary and metric units to measure b) liquid volume in cups, pints, quarts, gallons, and liters;

Linguistic Complexity Language Forms and Conventions Vocabulary Which unit would you use to measure cup-cups Cup, Pint, Quart, Gallon, liter, Volume ___? You would measure ___ using gallon-gallons ___. measure-measurement Which is the best estimate for ___? Why? capacity (liters, cups, pints, quarts, and gallons) How would you measure the capacity of How would you measure the capacity of a a bathtub? swimming pool

In cups or pints

28. Temperature 3.13 The student will read temperature to the nearest degree from a Celsius thermometer and a Fahrenheit thermometer. Real thermometers and physical models of thermometers will be used.

Linguistic Complexity Language Forms and Conventions Vocabulary What tool would you use to measure measure-measurement Temperature, Celsius, Fahrenheit, temperature? To measure Thermometer temperature you use a ___. What temperature does this thermometer show? Which piece of clothing would be good to wear on a day that is ___ degrees?

20°C (I wrote ‘C’ because this thermometer is measuring celcious.)

29. Telling time 3.11 The student will a) tell time to the nearest minute, using analog and digital clocks; and Linguistic Complexity Language Forms and Conventions Vocabulary How many minutes/ hours/ days / a.m.=morning Hours, Minutes, Half-hour, Quarter weeks/ months are in a hour/ day / p.m.=afternoon/night hour, Hour hand, Minute hand, Analog week/ month/ year? hour-hours clock, Digital clock, a.m., p.m., What time does this clock show? The Elapsed time time is ___. The hour/minute hand is showing ____. 30. Elapsed Time 3.11 The student will b) determine elapsed time in one-hour increments over a 12-hour period. Linguistic Complexity Language Forms and Conventions Vocabulary How many minutes/ hours/ days / a.m.=morning Hours, Minutes, Half-hour, Quarter weeks/ months are in a hour/ day / p.m.=afternoon/night hour, Hour hand, Minute hand, Analog week/ month/ year? hour-hours clock, Digital clock, a.m., p.m., What time does this clock show? The Elapsed time time is ___. The hour/minute hand is showing ____. If Jeidi went to a movie at 2:45 and it lasted for Jimmy’s art class started at this time. two hours, what time did the movie end?

4:45

His class lasts for 3 hours. What time did his class end?

9:30

Summer Camp starts at this time.

Delia started reading at 3:30 after school. She read for two hours. What time did she finish reading?

Camp lasts for 6 hours. What time does it end?