Worksheet 2.1 Number Systems: Complex Numbers

Maths Quest Maths C Year 11 for Queensland Chapter 2 Number systems: complex numbers WorkSHEET 2.1 1

WorkSHEET 2.1 Number systems: complex numbers Name: ______

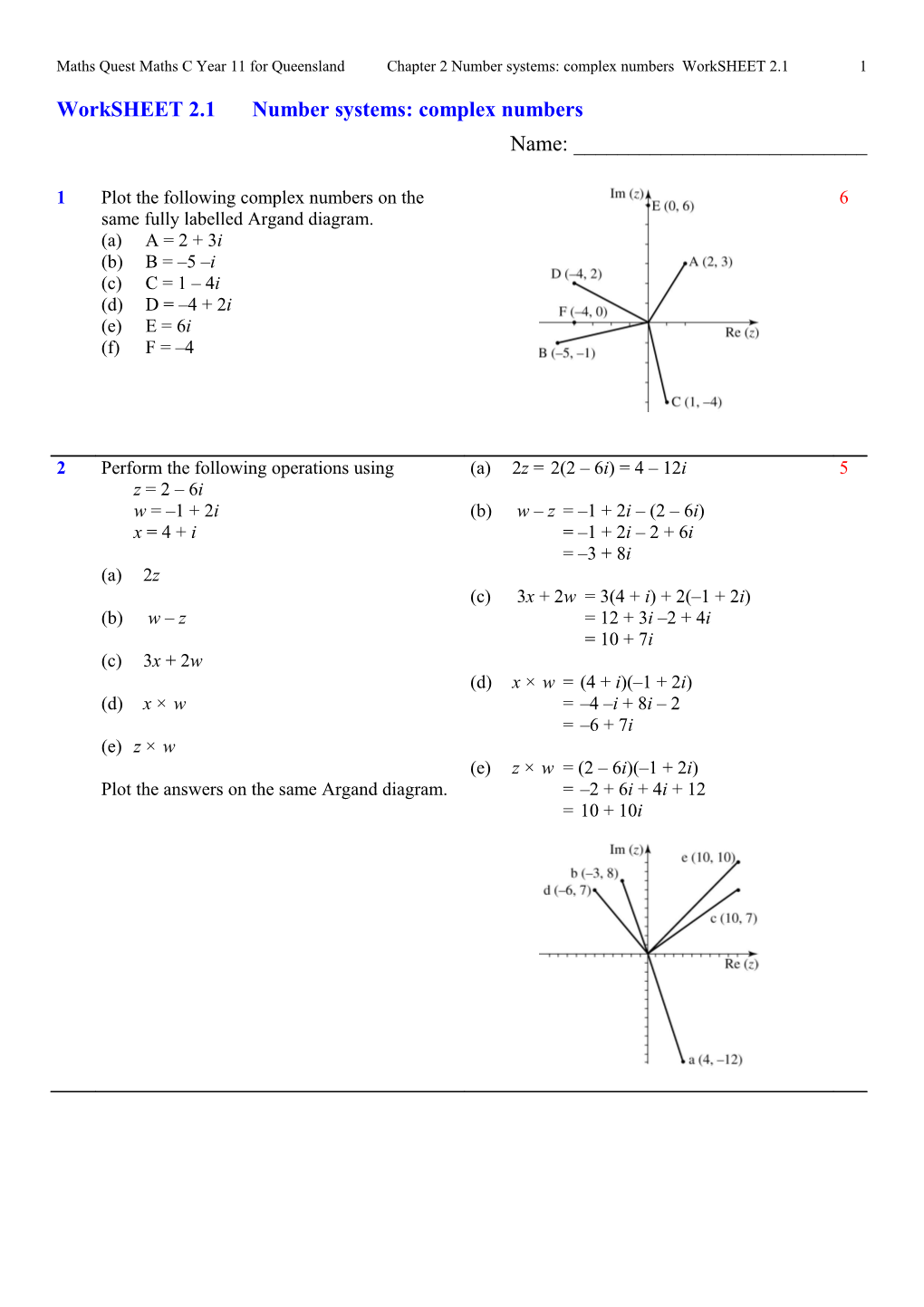
1 Plot the following complex numbers on the 6 same fully labelled Argand diagram. (a) A = 2 + 3i (b) B = –5 –i (c) C = 1 – 4i (d) D = –4 + 2i (e) E = 6i (f) F = –4

2 Perform the following operations using (a) 2z = 2(2 – 6i) = 4 – 12i 5 z = 2 – 6i w = –1 + 2i (b) w – z = –1 + 2i – (2 – 6i) x = 4 + i = –1 + 2i – 2 + 6i = –3 + 8i (a) 2z (c) 3x + 2w = 3(4 + i) + 2(–1 + 2i) (b) w – z = 12 + 3i –2 + 4i = 10 + 7i (c) 3x + 2w (d) x × w = (4 + i)(–1 + 2i) (d) x × w = –4 –i + 8i – 2 = –6 + 7i (e) z × w (e) z × w = (2 – 6i)(–1 + 2i) Plot the answers on the same Argand diagram. = –2 + 6i + 4i + 12 = 10 + 10i Maths Quest Maths C Year 11 for Queensland Chapter 2 Number systems: complex numbers WorkSHEET 2.1 2

3 Find the modulus of each of the following (a) z  22  (5)2 4 complex numbers:  4  25 (a) z = 2 – 5i  29 (b) w = –3 + 6i

(c) y = –6 + i (b) w  (3)2  62 (d) x = 4  9  36  45  3 5

(c) y  (6)2  12  36  1  37

(d) |x| = 4

4 Sketch the following complex numbers then 4 find the argument and principal argument of each:

(a) z = 1 – 4i

(b) w = –2 – 7i

(c) y = 3 + 4i

(d) x = –5i   4  (a) arg(z)  tan 1    1   1.33 Arg(z)  1.33

  7  (b) arg(w)  tan 1     2   1.29 Arg(w)  1.29   1.85 Maths Quest Maths C Year 11 for Queensland Chapter 2 Number systems: complex numbers WorkSHEET 2.1 3

 4  (c) arg(y)  tan 1    3   0.64 Arg(y)  0.64

3 (d) arg(x)  2  Arg(x)    2

5 Sketch the following complex numbers and (a) 4 express them in polar form:

(a) z = 2 + 3i

(b) w = –4 –2i

(c) y = –3 + i z  22  32  4  9  13  3  (d) x = 5 – 5i arg(z)  tan 1    0.98 (b)  2  z  13 cis 0.98

w  (4) 2  (2) 2  16  4  20  2 5   2  arg(w)  tan 1    0.46   4  Arg(w)  0.46   2.68 w  2 5 cis (2.68) (c)

y  (3) 2 12  9 1  10  1  arg(y)  tan 1    0.32   3  Arg(y)  0.32    2.82 y  10 cis 2.82 (d) Maths Quest Maths C Year 11 for Queensland Chapter 2 Number systems: complex numbers WorkSHEET 2.1 4

x  52  (5)2  25  25  50  5 2   5   arg(x)  tan 1     5  4

6 Use common trigonometric ratios in their (a) 4 relevant triangles (but no formal calculator work) to express the following in polar form:

(a) z = 2 – 2i

(b) w =  1  3i    z  2 2 cis   (c) y = 4 3  4i  4  (b) (d) x =  5  5 i

 2  w  2 cis    3  (c)

 y  8 cis 6 (d)

3 x  10 cis 4