Sangaku--Japanese Mathematics and Art in the 18Th,19Th and 20Th Centuries
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Keita Matsunaga
720 N. Highland Ave., Los Angeles, CA 90038 | T: 323 450 9409 | www.nonaka-hill.com Keita Matsunaga Biography Born in Tajimi, Japan (an area well known for ceramics), in 1986, Keita Matsuaga currently lives and works in both Tajimi and Kani in Gifu prefecture. The son of ceramists, his artistic training includes studying architecture at Meijo University, (2010), completing the Tajimi City Ceramics Design Laboratory (2013), and graduation from the Kanazawa Utsatsuyama Crafts Workshop (2016). Matsunaga has shown extensively across Japan in both a gallery setting and in biennales, and has won several awards including the Takaoka Contemporary Craft Competition (2013). Matsunaga’s ceramic sculptures are a contemporary take on organic forms, inspired by shapes and textures found in nature. Even at a young age, his comprehension of glaze is apparent, seen in the fearless color schemes found on each work. Changing method with each body of work, his evolving artistic practice is indicative of his education – an impressive dedication to keep learning. Matsunaga’s work has its roots in Japanese ceramic tradition but finished with unexpected detail and technique, resulting in a look that is decisively his own. 1986 Born in Tajimi, Gifu 2010 Graduated from Meijo University,Architecture Course 2013 Graduated from Tajimi City Pottery Design And Technical Center 2016 Graduated from Kanazawa Utatsuyama Kogei Kobo 2019 Artist-in-residence at the Shigaraki Ceramic Cultural Park Artist-in-Residence at California State University, Long Beach Selected Solo -

Prime Minister Abe in Florida
Prime Minister Abe in Florida Japan's prime minister visited Florida to attend three summit meetings with U.S. President Donald J. Trump on April 17-18. Read more below: Credit: Cabinet Public Relations Office Link Japan to Host 2019 G-20 Summit in Osaka In 2019, Japan will host the Group of 20 leaders' summit in Osaka on June 28-29. Ministerial-level meetings will be held across Japan at venues in Fukuoka, Hokkaido, Aichi and other prefectures. Information on this year's G20 Buenos Aires meetings below: Link 1 Japanese Ambassador to the U.S. in Los Angeles Japan’s Ambassador Shinsuke Sugiyama visited L.A., with trip highlights including a meeting with Mayor Eric Garcetti and a stop at Japan House Los Angeles. The ambassador also attended the Japanese American National Museum’s 2018 Gala Dinner and Silent Auction where he met JANM Board of Trustees Chair Hon. Norman Mineta and Senator Mazie K. Hirono. Link Recipients of Spring 2018 Commendation Mr. Ellis Krauss (left) will be conferred the Order of the Rising Sun, Gold Rays with Neck Ribbon for his contribution to promoting academic research on Japan, and academic exchange between Japan and the United States. Mr. Ernest Doizaki (right) will be conferred the Order of the Rising Sun, Gold and Silver Rays for contributing to strengthening economic relations and mutual understanding between Japan and the United States. Link MEXT Scholarship Applications Available 2 Applications for the 2019 Research Students Scholarship, 2019 Undergraduate Students Scholarship, and 2019 Specialized Training College Students Scholarship are now available. Established in 1954, the MEXT Scholarship Program has enabled more than 102,000 students from 160 countries and regions worldwide to study in Japan. -

Tajimi Ko-Uta (Gifu Prefecture, Japan)
140 Tajimi ko-uta (Gifu Prefecture, Japan) Tajimi is a city located in southern Gifu prefecture, close to the border of Aichi prefecture. It became a city in 1940 and the region has been known for Mino- yaki ceramics since the railway was opened in 1900. This city can be divided into four districts according to the type of ceramic product it produces. The song is about the birthplace of Mino-yaki ceramics. “Tajimi Kouta” is performed by the public each August on the anniversary of the city’s founding or at Bon festivals. Pronunciation: tah-jee-mee koh-tah Music: 4/4 meter Japanese Music CD, Track 1 Formation: Individual dancers facing ctr, hands at sides. Steps & Styling: Bose hando: Arms bent at elbow, forearms horizontal with palms down at chest height, R arm above L. Cho: a short, soft clap of the hands; Chon: a hard, long clap of the hands. Fujiyama: Arms form a mountain (Mt. Fujiyama), palms down, fingers touching in front of the face. Fusenagashi: Swing both arms down and to the R. Can be done with same arm movements to the L side. Soenobashi: R arm straight in front, palm down; L arm bent with hand on R elbow. Can be done with opp. hand position. Ryote age kazashi: Raise arms above head with palms up to form a circle (moon). This movement may take two cts or be spread out over 4-6 cts. Tate kazashi: R arm extended fwd at shldr height, palm down. L arm is bent at elbow with palm facing twd face. -

Announcements from Gifu Prefecture”
英語版/English Edition Pref. Gov. PR Television Show Gifu Prefecture Public Relations ●Prefecture Population “Gifu Pref. Hot Line” Now airing people (up 695) 1,992,318 (Air Date) Thurs. 18:53~18:57 ※as of May 1, 2019 Announcements from (Rerun Date) Tues. 21:54~21:58 ※stats in parentheses are a comparison with the previous month “Announcements from Gifu Prefecture” Gifu Prefecture also available via data broadcast on Gifu Facebook「Seiryu no Kuni Gifu」 Channel (Channel 8)! August, 2019 Dispatching information at Minamo Dayori!! 「岐阜県からのお知らせ」も配信中! Press the 岐阜県 ミナモだより Search D button to get local information! This Month’s Highlights Construction Work to Start on the New Prefectural Government Office Building Construction of the new prefectural government office building (administrative building) is starting, with the aim of completing construction by 2022. As the center of the Prefecture’s operations in the event of a disaster, the new building will be quake-resistant, and will take into consideration the principles of Exterior image of new building universal design. The new prefectural government building will be approchable and easy-to-use, aiming to offer an even higher Talks by Prefectural Government Employees quality of civil service than up to this point. Prefectural government employees are available to give talks about the new Overview of the New Government Office Building government office building construction project Concept at the request of prefectural residents. Please The Base of Prefectural Government: A reliable base carrrying -

By Municipality) (As of March 31, 2020)
The fiber optic broadband service coverage rate in Japan as of March 2020 (by municipality) (As of March 31, 2020) Municipal Coverage rate of fiber optic Prefecture Municipality broadband service code for households (%) 11011 Hokkaido Chuo Ward, Sapporo City 100.00 11029 Hokkaido Kita Ward, Sapporo City 100.00 11037 Hokkaido Higashi Ward, Sapporo City 100.00 11045 Hokkaido Shiraishi Ward, Sapporo City 100.00 11053 Hokkaido Toyohira Ward, Sapporo City 100.00 11061 Hokkaido Minami Ward, Sapporo City 99.94 11070 Hokkaido Nishi Ward, Sapporo City 100.00 11088 Hokkaido Atsubetsu Ward, Sapporo City 100.00 11096 Hokkaido Teine Ward, Sapporo City 100.00 11100 Hokkaido Kiyota Ward, Sapporo City 100.00 12025 Hokkaido Hakodate City 99.62 12033 Hokkaido Otaru City 100.00 12041 Hokkaido Asahikawa City 99.96 12050 Hokkaido Muroran City 100.00 12068 Hokkaido Kushiro City 99.31 12076 Hokkaido Obihiro City 99.47 12084 Hokkaido Kitami City 98.84 12092 Hokkaido Yubari City 90.24 12106 Hokkaido Iwamizawa City 93.24 12114 Hokkaido Abashiri City 97.29 12122 Hokkaido Rumoi City 97.57 12131 Hokkaido Tomakomai City 100.00 12149 Hokkaido Wakkanai City 99.99 12157 Hokkaido Bibai City 97.86 12165 Hokkaido Ashibetsu City 91.41 12173 Hokkaido Ebetsu City 100.00 12181 Hokkaido Akabira City 97.97 12190 Hokkaido Monbetsu City 94.60 12203 Hokkaido Shibetsu City 90.22 12211 Hokkaido Nayoro City 95.76 12220 Hokkaido Mikasa City 97.08 12238 Hokkaido Nemuro City 100.00 12246 Hokkaido Chitose City 99.32 12254 Hokkaido Takikawa City 100.00 12262 Hokkaido Sunagawa City 99.13 -
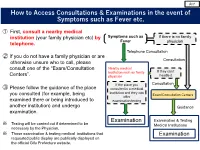
How to Access Consultations & Examinations in the Event Of
英語 How to Access Consultations & Examinations in the event of Symptoms such as Fever etc. ① First, consult a nearby medical institution (your family physician etc) by Symptoms such as If there is no family Fever telephone. physician Telephone Consultation ② If you do not have a family physician or are Consultation otherwise unsure who to call, please consult one of the “Exam/Consultation Nearby medical institution such as family If they can’t Centers”. physician handle it If the place you Consultation ③ Please follow the guidance of the place consulted is a medical institution and they can you consulted (for example, being Exam/Consultation Centers offer examined there or being introduced to examination/testing another institution) and undergo Guidance examination. Examination & Testing ※ Examination Testing will be carried out if determined to be Medical Institutions necessary by the Physician. ※ Those examination & testing medical institutions that Examination requested public display are publically displayed on the official Gifu Prefecture website. List of Exam/Consultation Centers ○Reception: 24-hour ※Telephone reception only outside of regular hours( 9:00 – 17:00 weekdays) Test/Consultation Center Tel. Number Etc Area Covered 058-380-3004 Hashima, Kakamigahara, Yamagata, Mizuho & Gifu Health Center FAX: 058-371-1233 Motosu Cities, Hashima-gun and Motosu-gun 0584-73-1111(Ext. 273) Ogaki & Kaizu Cities, Yoro-gun, Fuwa-gun, Seino Health Center FAX: 0584-74-9334 Anpachi-gun and Ibi-gun 0575-33-4011(Ext. 360) Seki Health Center Seki, Mino & Gujo Cities FAX: 0575-33-4701 0574-25-3111(Ext. 358) Kamo Health Center Mino-kamo & Kani Cities, Kamo-gun and Kani-gun FAX: 0574-28-7162 0572-23-1111(Ext. -

“4Th Wave” State of Emergency Measures (Extract)
th “4 Wave” State of Emergency Measures (Extract) Originally published on April 23th 2021 Revised on May 28th 2021 COVID-19 Infection Measures Headquarters Gifu Prefectural Government Implementation Period: Until June 20th (Sunday) 2021 Measure 1 Thorough Observance of “New Behaviour Guidelines” First “continue to thoroughly implement basic infection prevention measures (the wearing of masks, hand hygiene, avoidance of the three Cs and management of your physical condition).” These same measures can help prevent infection of new variants as well. Even those who are vaccinated should continue to observe these measures, as vaccinations are not 100% effective. (1) To all Prefectural Residents ① Avoid travel & outings (in particular young people) ・ Avoid “non-urgent and unnecessary travel & outings” at all times of day ・ Also refrain from “non-urgent and unnecessary travel between Prefectures”. In particular, avoid travel to and from areas where states of emergency have been declared or which have been designated as special measures areas to prevent further infections such as Aichi. ② Eating & Drinking Measures ・ Avoid use of eating & drinking businesses which do not thoroughly implement infection prevention measures and/or comply with the demand for a shortening in business operating hours. ・ Avoid eating & drinking in large groups or over long times including in the home. Do not drink heavily or speak loudly and wear masks when talking. Be cautious even with your family or partner. ・ High infection risk behaviours such as the drinking of -

Japanese Language Classes Run by Volunteers in Gifu Prefecture
Japanese Language Classes run by Volunteers in Gifu Prefecture Course Information Are they recruiting Can I bring Region Group Name Contact Venue Class Level volunteers/teachers? Term Dates Day/Time Course Fees etc Enrollment Type of Class young children? Can I observe a lesson? Minna no Mori Gifu Media ●Beginners I/II ●Course Fee: Cosmos Library 1F, Mon, Wed ・Beginner Ⅰ/Ⅱ Japanese for Foreign Atsumaru Studio, Waiwai 18:30 - 20:30 \13,000 per term Residents Gifu International Circle Tues, Thurs (30 classes) March, ●Beginners I/II Exchange Association 40-5 Tsukasa-machi, Gifu- 18:30 - 20:30 ・Beginner EX September (also Not recruiting, ①Apr - Jul Classroom-style 1 ●Beginners EX Tel: 058-263-1741 shi ※2 \6,500 per term possible to join Beginner No observation ②Oct - Feb (3 classes) Email: (2 mins walk from Media classes/week (15 classes) in the middle of possible. (for those who can read and [email protected] Cosmos bus stop) ●Course Materials: a term) write hiragana and katakana) Parking available (※free ●Beginners EX \2,430 per term Extra Materials: for two hours, charged Fri \1,950 per term over two hours) 18:30 - 20:30 Inoguchi Kakehashi no Kai One-on-one Recruiting, Fujiko Takahashi Wednesdays Beginner to 2 Japanese Volunteer Class Same as above - Free Any time tutoring or small No observation Tel: 090-5455-6988 19:00 - 20:30 advanced groups possible. Email: [email protected] Gifu International Center Gifu City Fureai Nihongo Japanese Gifu Chunichi Building 2F Class One-on-one Recruiting, Fureai Nihongo Japanese 1-12 Yanagase Dori, Gifu-shi Sundays Introductory to 3 Hiroyuki Moriya - \200 per session Any time tutoring, small Yes observation Class (By bus: take the bus from JR 10:00 - 11:30 advanced groups possible. -

GIS and Edna Analysis System Successfully Used to Discover New Habitats of Rare Salamander 6 September 2019
GIS and eDNA analysis system successfully used to discover new habitats of rare salamander 6 September 2019 It has been reported that there are approximately 50 Hynobius species of salamander worldwide, around 30 of which are endemic to Japan. Hynobius vandenburghi (until recently known by its previous classification of H. nebulosus), is only found in central and western Japan, with Gifu Prefecture marking the northeast limit of the species' distribution (Figure 2). However, like approximately 60 percent of amphibian species in Japan, it falls under the ranking of critically endangered and vulnerable species, mainly due to habitat decline. Only three sites providing habitats for Yamato salamanders had been discovered in Gifu Prefecture up until recently. A Yamato salamander (Hynobius vandenburghi) and its egg sac (lower right). Credit: Koki Tsunekawa (Nature and Science Club Bioscience team leader, Gifu Senior High School 3rd grade) A research team has successfully identified an unknown population of the endangered Yamato salamander (Hynobius vandenburghi) in Gifu Prefecture using a methodology combining GIS and eDNA analysis. This method could be applied to other critically endangered species, and could also be used to locate small organisms that are A distribution map of Hynobius vandenburghi. Credit: difficult to find using conventional methods. Kobe University The study was conducted by students from the Bioscience team in Gifu Senior High School's Nature and Science Club (which has been The research team used a combined methodology conducting research into the species for 13 years). of GIS and eDNA analysis with the aim of They were supervised by teachers and aided by discovering more Yamato salamander habitats. -

Digital Newsletter (PDF)
GO GIFU Gifu Prefecture Tourism and Event Newsletter Vol. 41 Spring 2019 The iconic hana mikoshi making their way through the old streets of Mino City’s Udatsu Wall Historical District Unique festivals, sakura-themed merchandise at local convenience stores, warm weather and sprouting vegetation (also note the sudden increase of white masks amongst hay fever sufferers) are all signs of the coming of spring here in Gifu. With this newsletter we hope to introduce a few of the festivals and other events here that one can enjoy during the spring. Make sure and check out our Facebook page for upcoming events and other Gifu-related news not mentioned in this newsletter. Safe Travels! Mino Festival 美濃まつり Are those cherry trees?! Not quite. The annual Mino Festival is the only place where you can witness the beautiful hana mikoshi (“flower shrines” in English), which are aptly named for their resemblance of dancing cherry blossom trees. The 30 hana mikoshi of varying sizes, which are paraded down Mino City’s Udatsu Wall Historical District, have hundreds of bamboo poles “Dancing” hana mikoshi that are adorned with pink Mino Washi paper. The Mino Festival showcases Date: April 13~14 the beauty of Mino Washi, a Location: Udatsu Wall Historical District, Mino City traditional style of Japanese Directions: 10-minute walk from the Nagaragawa Railway Mino-shi paper that has been produced in Station OR 1-min walk from the “Udatsu no Machinami Dori” bus stop on the Gifu Bus Mino Line; from JR Gifu Station bus platform 14 Mino City for over 1,300 years! take a B87 bus towards “Chuno Chosha” (~60 min, 990 yen) Go Gifu Page 1 Spring 2019 Yatai festival floats making their Takayama Spring Festival way across Takayama’s iconic 春の高山祭 Nakabashi Bridge The Takayama Festival is considered to be one of Japan’s Three Most Beautiful Festivals and holds a history of over 400 years. -
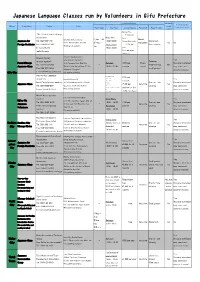
Japanese Language Classes Run by Volunteers in Gifu Prefecture
Japanese Language Classes run by Volunteers in Gifu Prefecture Course Information Can I bring Are they recruiting Region Group Name Contact Venue young Term Dates Day/Time Course Fees etc Enrollment Type of Class volunteers/teachers? children? Course Fee: Gifu International Exchange \13,000 per Association Mon, Wed term Gifu City Culture Center ①Apr - Jul March, Japanese for Tel: 058-263-1741 18:30-20:30 Course Materials: Classroom 5-7-2 Kanda-machi, Gifu-shi ② Oct - Septembe No No Foreign Residents Fax: 058-263-1741 Tues, Thurs \2,430 per (two classes) (Parking not available) Jan r E-mail: gifucity- 18:30-20:30 year [email protected] Extra Materials (optional): Gifu International Center Hiroyuki Moriya Gifu Chunichi Building 2F Yes (private number) Tutoring: Fureai Nihongo 1-12 Yanagase Dori, Gifu City Sundays \200 per Every (Anyone interested Tel: 090-9023-3541 - (One-on-one, Yes Japanese Class (By bus: take the bus from JR Gifu 10:00 - 11:40 session month may come and Fax: 058-273-3051 small groups) Station to Yanagase) observe lessons) Gifu City E-mail: [email protected] (No parking available) Ayu-no-Kai Japanese Tues, Wed, Thurs, Fri \200 per Volunteers Heartful Square G 10:00 - 11:30 Yes 13:00 - 14:30 session Izumi Fujita (private number) 1-10-23 Hashimoto-cho, Gifu-shi Wednesdays One-on -one (Anyone interested Japanese Class - (\100 per Any time No Tel: 090-9935-8571 (East side of JR Gifu Station) 19:00 - 20:30 tutoring may come and Saturdays (Primary school students session for the Paid parking available E-mail: [email protected] only) observe lessons) childrens' class) net.ne.jp 14:00 - 16:00 Misaki Mutou (private Gifu Kita Seishounen Kaikan number) Wed, Thurs Yes Niji no Wa 3-19-18 Fukumitsu-Higashi, Gifu-shi Tel: 090-6580-6176 10:00 - 15:00 \150 per One-on-one (Anyone interested Japanese (3 mins walk from Fukumitsu bus - Any time No Emiko Kimura (private Saturdays session tutoring may come and Volunteers stop (No. -

Area Locality Address Description Operator Aichi Aisai 10-1
Area Locality Address Description Operator Aichi Aisai 10-1,Kitaishikicho McDonald's Saya Ustore MobilepointBB Aichi Aisai 2283-60,Syobatachobensaiten McDonald's Syobata PIAGO MobilepointBB Aichi Ama 2-158,Nishiki,Kaniecho McDonald's Kanie MobilepointBB Aichi Ama 26-1,Nagamaki,Oharucho McDonald's Oharu MobilepointBB Aichi Anjo 1-18-2 Mikawaanjocho Tokaido Shinkansen Mikawa-Anjo Station NTT Communications Aichi Anjo 16-5 Fukamachi McDonald's FukamaPIAGO MobilepointBB Aichi Anjo 2-1-6 Mikawaanjohommachi Mikawa Anjo City Hotel NTT Communications Aichi Anjo 3-1-8 Sumiyoshicho McDonald's Anjiyoitoyokado MobilepointBB Aichi Anjo 3-5-22 Sumiyoshicho McDonald's Anjoandei MobilepointBB Aichi Anjo 36-2 Sakuraicho McDonald's Anjosakurai MobilepointBB Aichi Anjo 6-8 Hamatomicho McDonald's Anjokoronaworld MobilepointBB Aichi Anjo Yokoyamachiyohama Tekami62 McDonald's Anjo MobilepointBB Aichi Chiryu 128 Naka Nakamachi Chiryu Saintpia Hotel NTT Communications Aichi Chiryu 18-1,Nagashinochooyama McDonald's Chiryu Gyararie APITA MobilepointBB Aichi Chiryu Kamishigehara Higashi Hatsuchiyo 33-1 McDonald's 155Chiryu MobilepointBB Aichi Chita 1-1 Ichoden McDonald's Higashiura MobilepointBB Aichi Chita 1-1711 Shimizugaoka McDonald's Chitashimizugaoka MobilepointBB Aichi Chita 1-3 Aguiazaekimae McDonald's Agui MobilepointBB Aichi Chita 24-1 Tasaki McDonald's Taketoyo PIAGO MobilepointBB Aichi Chita 67?8,Ogawa,Higashiuracho McDonald's Higashiura JUSCO MobilepointBB Aichi Gamagoori 1-3,Kashimacho McDonald's Gamagoori CAINZ HOME MobilepointBB Aichi Gamagori 1-1,Yuihama,Takenoyacho