Compressible Flow with Shock Wave

ME 362 Compressible Flow with Shock Wave Page 1 of 4

Solution:

To show that a normal shock wave exists within the duct, we need to prove that

PE,exit < Pback < PA,exit

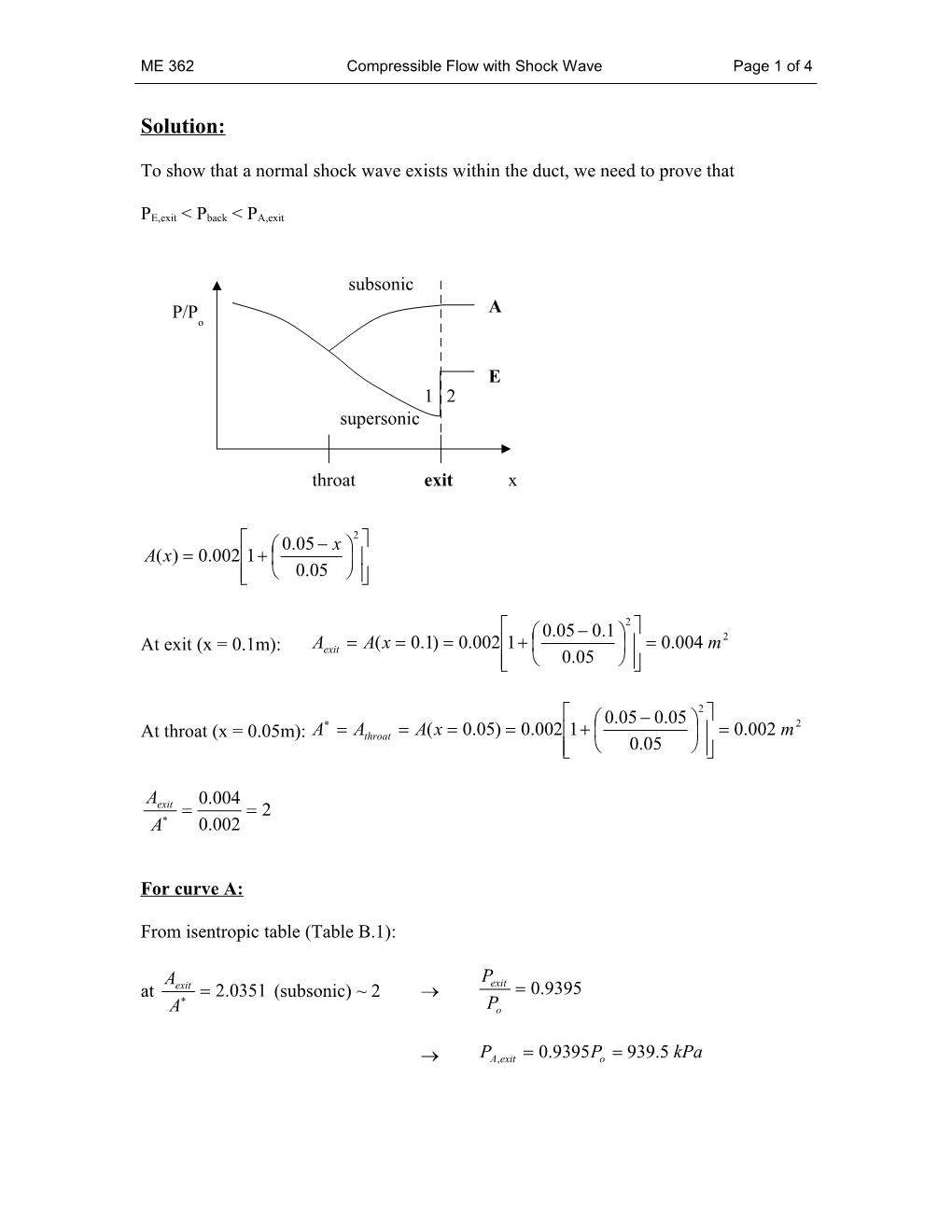
subsonic P/P A o

E 1 2 supersonic

throat exit x

2   0.05  x   A(x)  0.0021      0.05  

 2   0.05  0.1 2 At exit (x = 0.1m): Aexit  A(x  0.1)  0.0021     0.004 m   0.05  

 2    0.05  0.05  2 At throat (x = 0.05m): A  Athroat  A(x  0.05)  0.0021     0.002 m   0.05  

A 0.004 exit   2 A 0.002

For curve A:

From isentropic table (Table B.1):

A P exit exit  0.9395 at   2.0351 (subsonic) ~ 2  A Po

 PA,exit  0.9395Po  939.5 kPa ME 362 Compressible Flow with Shock Wave Page 2 of 4

For curve E:

Before shock (isentropic, supersonic):

A at exit  2.0050 (supersonic) ~ 2  Ma  2.2 A 1

Across shock (nonisentropic):

From shock table (Table B.2):

P A o2  0.6281 2 at Ma1  2.2  and   1.5920 Po1 A1

 2 A1  Athroat  0.002 m

  2 A21.5920 A 1  1.5920  0.002  0.003184 m

After shock (isentropic, subsonic):

Aexit 0.004    1.2563 A2 0.003184

Aexit Pexit at   1.2403 (subsonic)   0.8082 A2 Po2 ~ 1.2563 P P P  exit  exit o2  0.8082 0.6281  0.5076 Po Po2 Po1

 PE,exit  0.5076Po  507.6 kPa

PE,exit  507.6 kPa < Pback  650 kPa < PA,exit  939.5 kPa

 Normal shock exists within the nozzle [Ans.] ME 362 Compressible Flow with Shock Wave Page 3 of 4

Iterative procedure for locating normal shock wave:

sonic subsonic 1 2 supersonic

throat x exit x shock

Before shock (isentropic, supersonic): at x = 0.075m:

 2   0.05  0.075  2 A1  Ashock  A(x  0.075)  0.0021     0.0025 m   0.05  

A 0.0025 1   1.25 A 0.002

A at 1  1.2502 (supersonic) ~ 1.25  Ma  1.6 A 1

Across shock (nonisentropic):

From shock table (Table B.2):

P A o2  0.8952 2 at Ma1  1.6  and   1.1171 Po1 A1

  2 A21.1171 A 1  1.1171  0.002  0.00223 m ME 362 Compressible Flow with Shock Wave Page 4 of 4

After shock (isentropic, subsonic):

Aexit 0.004    1.7937 A2 0.00223

Aexit Pexit at   1.8229 (subsonic) ~ 1.7937   0.9231 A2 Po2

Pexit Pexit Po2   0.9231 0.8952  0.8264  Pexit  0.8264Po  826.4 kPa [Ans.] Po Po2 Po1

Determine if correct shock position is upstream or downstream of x = 0.075 m:

Pexit826.4 kPa  P back  650 kPa  correct shock position > x = 0.075 m

 correct shock position is further downstream [Ans.]

P /P P > P back o exit back sonic P = P P exit back back shock

x x x x throat shock exit x = 0.075m