Nitrogen Footprint in a Long-Term Observation of Forest Growth Over the Twentieth Century

Online Resource

Nitrogen footprint in a long-term observation of forest growth over the twentieth century. Trees – structure and function

Jean-Daniel BONTEMPS, AgroParisTech, ENGREF, UMR 1092 INRA/AgroParisTech Laboratoire d'Etude des Ressources Forêt-Bois (LERFoB), 14 rue Girardet, 54000 Nancy, France. jean- [email protected]

Jean-Christophe HERVÉ, Inventaire Forestier National (IFN), Direction Technique, Domaine des Barres, 45290 Nogent-sur-Vernisson, France. [email protected]

Jean-Michel LEBAN, INRA, UMR 1092 INRA/AgroParisTech Laboratoire d'Etude des Ressources Forêt-Bois (LERFoB), Centre de Nancy, 54280 Champenoux, France. [email protected]

Jean-François DHÔTE, Office National des Forêts (ONF), Direction Technique et Commerciale Bois, Boulevard de Constance, 77300 Fontainebleau, France. [email protected]

Corresponding author: Jean-Daniel BONTEMPS, [email protected]

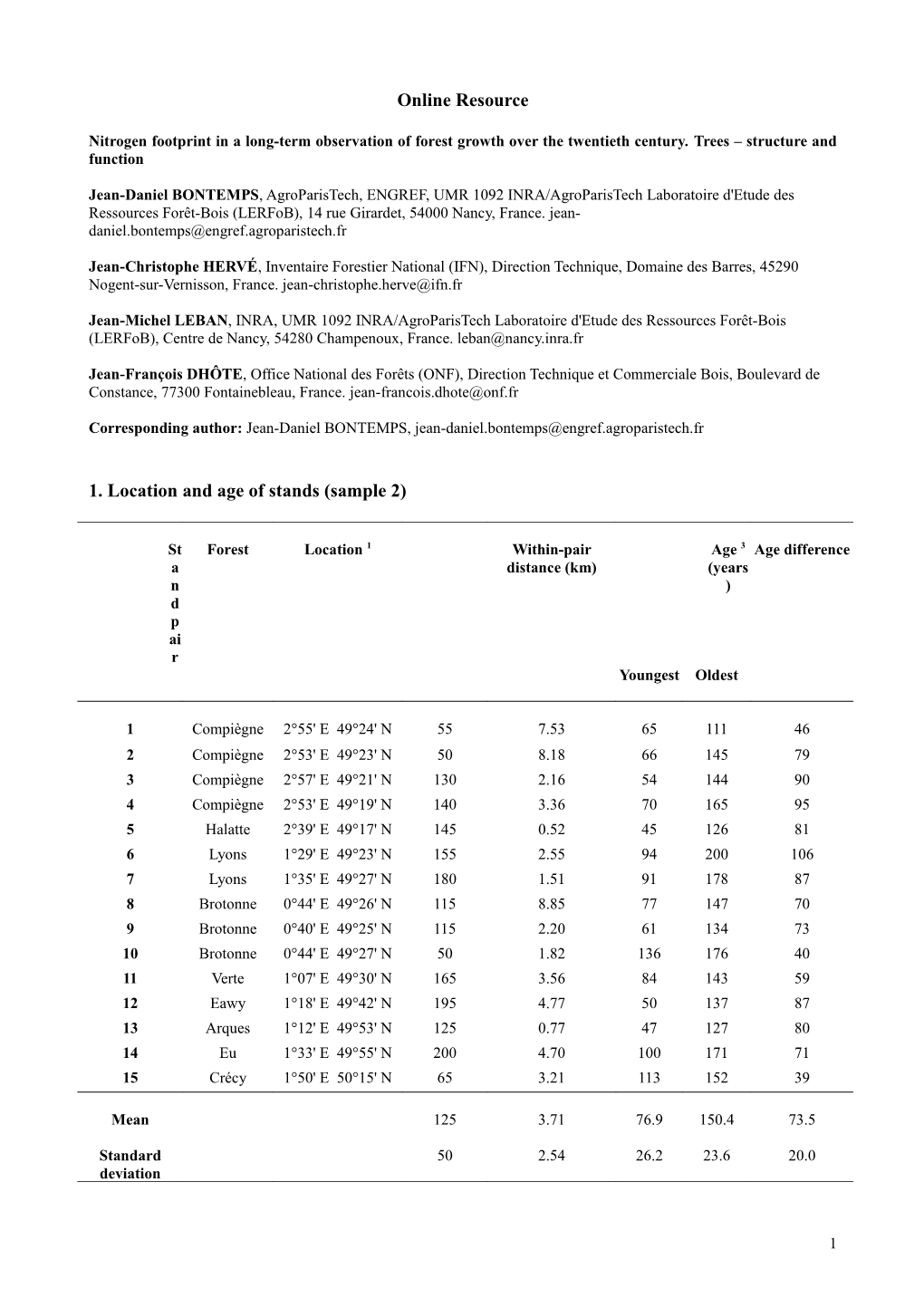
1. Location and age of stands (sample 2)

St Forest Location 1 Within-pair Age 3 Age difference a distance (km) (years n ) d p ai r Youngest Oldest

1 Compiègne 2°55' E 49°24' N 55 7.53 65 111 46 2 Compiègne 2°53' E 49°23' N 50 8.18 66 145 79 3 Compiègne 2°57' E 49°21' N 130 2.16 54 144 90 4 Compiègne 2°53' E 49°19' N 140 3.36 70 165 95 5 Halatte 2°39' E 49°17' N 145 0.52 45 126 81 6 Lyons 1°29' E 49°23' N 155 2.55 94 200 106 7 Lyons 1°35' E 49°27' N 180 1.51 91 178 87 8 Brotonne 0°44' E 49°26' N 115 8.85 77 147 70 9 Brotonne 0°40' E 49°25' N 115 2.20 61 134 73 10 Brotonne 0°44' E 49°27' N 50 1.82 136 176 40 11 Verte 1°07' E 49°30' N 165 3.56 84 143 59 12 Eawy 1°18' E 49°42' N 195 4.77 50 137 87 13 Arques 1°12' E 49°53' N 125 0.77 47 127 80 14 Eu 1°33' E 49°55' N 200 4.70 100 171 71 15 Crécy 1°50' E 50°15' N 65 3.21 113 152 39

Mean 125 3.71 76.9 150.4 73.5

Standard 50 2.54 26.2 23.6 20.0 deviation

1 1 Mean geographic coordinates of stand pairs (ED 50 system), 2 mean elevation of stand pairs (a.s.l.), 3 stand age in 1998

2. Growth equations tested

Differential expressions of growth equations (f1)

Equations parameterised with K as the height asymptote (metres) and Sb as the maximal growth rate

(metres/year):

1m  m  dH 0  H 0   H 0   Richards:  Sb C m   1    dt  K    K  

(m-1)/m where Cm = (1-m) / m

1m 1m dH 0  H 0   H 0   Hossfeld:  Sb Cm   1  dt  K   K 

m–1 – (1+m) where Cm = 4 (1–m) (1+m)

1m dH 0 H 0  K  - Korf:  Sb C m ln  dt K  H 0 

where Cm = exp [ (1+m) (1 – ln (1+m)) ]

-1 Expressions for the integrated form (F1 )

-1 All equations admit close-form solutions for F1 and F1 (integration on time interval [t-1, t]):

1 m   H (t ) m  R m C  - Richards:   0 1   b m   H 0 (t)  K 1    1 exp  F2 (t)  F2 (t1 )   K   K      

K H 0 (t)  1 m  - Hossfeld: R m C  H (t )   m 1  b m F (t)  F (t )   0 1   K 2 2 1  K  H (t )    0 1  

2 1      m  m   R b mC m  K    - Korf: H 0 (t)  K exp  F2 (t)  F2 (t1 )  ln    K H (t )     0 1     

F = f (v) dv where 2  2 .

3. Cubic spline function of date (f2)

Cubic spline functions are piecewise continuous polynomials defined on successive time intervals.

These time intervals – or internodes – were set equal along calendar date. Different internodes were tested to assess decennial-order fluctuations (20, 15 and 10 years). The general expression is:

k1 k2 2 3 3 3 f 2 u  1 d1 u  d 2 u  d3 u   p k maxu  n k,0   pm k minu  n k,0 k1 k 0

where u = t – tb, d1, d2, d3, pk and pmk are spline parameters to be estimated, [0, n] is the base internode of spline (n = 20, 15 or 10), and n, k1 and k2 externally specify the width and number of spline intervals necessary to describe the entire period range covered. For instance with n = 15, nodes are located at dates 1870, 1885, 1900, 1915, …, 1990.

4. Growth-environment relationships – Sb estimates for sample 2

In sample 2, the best fit was obtained with the Korf equation. However, the difference was only -4.5

AIC units compared with the Hossfeld equation, also the most accurate in sample 1. For a clear comparison of regional growth-environment relationships, Sb estimates were extracted from a

Hossfeld-based model in sample 2.

Differences in Sb estimates from Korf- and Hossfeld- based models were investigated (see Figure

– below). The correlation between both estimates was 1 (p = 0). When Hossfeld Sb estimates were predicted from the Korf ones using simple linear regression, the intercept was not significant:

-3 Sb,Hossfeld = 0.9816; Sb,Korf (RSE = 2.5 10 m/year). Furthermore, the growth-environment relationship in sample 2 was insensitive to the set of Sb estimates considered.

3 Comparison of level 2 Sb estimates from a Korf- and Hossfeld-based model 5 5 . 0 0 5 . n 0 o i t a u 5 4 q . e 0 d l e f 0 s 4 . s 0 o H

5 ) r 3 . y / 0 m (

b 0 S 3 . 0 5 2 . 0

0.25 0.30 0.35 0.40 0.45 0.50 0.55

Sb (m/yr) - Korf equation