Unit 24 Single Sample Testing of Means

Elementary Statistics Triola, Elementary Statistics 11/e Unit 24 Single Sample Testing of Means

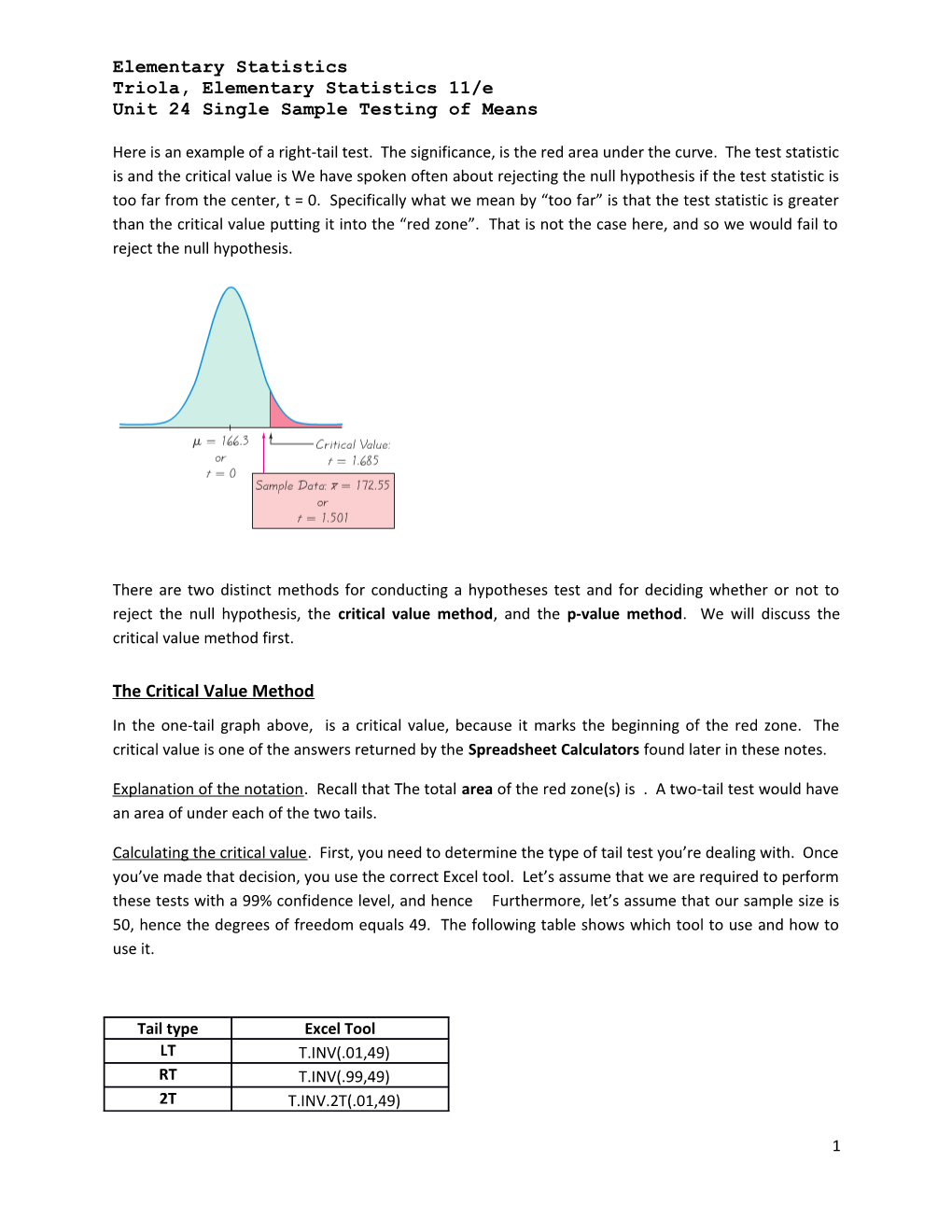
Here is an example of a right-tail test. The significance, is the red area under the curve. The test statistic is and the critical value is We have spoken often about rejecting the null hypothesis if the test statistic is too far from the center, t = 0. Specifically what we mean by “too far” is that the test statistic is greater than the critical value putting it into the “red zone”. That is not the case here, and so we would fail to reject the null hypothesis.

There are two distinct methods for conducting a hypotheses test and for deciding whether or not to reject the null hypothesis, the critical value method, and the p-value method. We will discuss the critical value method first.

The Critical Value Method In the one-tail graph above, is a critical value, because it marks the beginning of the red zone. The critical value is one of the answers returned by the Spreadsheet Calculators found later in these notes.

Explanation of the notation. Recall that The total area of the red zone(s) is . A two-tail test would have an area of under each of the two tails.

Calculating the critical value. First, you need to determine the type of tail test you’re dealing with. Once you’ve made that decision, you use the correct Excel tool. Let’s assume that we are required to perform these tests with a 99% confidence level, and hence Furthermore, let’s assume that our sample size is 50, hence the degrees of freedom equals 49. The following table shows which tool to use and how to use it.

Tail type Excel Tool LT T.INV(.01,49) RT T.INV(.99,49) 2T T.INV.2T(.01,49)

1 Unit 24 Single Sample Testing of Means

NOTE: There is no T.INV.RT unfortunately, so we have to use T.INV and use the Confidence Level for the Probability input. If you find this annoying, do not be concerned. In practice, you will be using the Spreadsheet Calculators which automatically handle this annoyance for you.

Question #1 Try this one by hand. A left-tail test, C.L. = 95% and n = 30. Find the critical value t*.

NOTE: We need to use the absolute value of when doing a two-tail test.

As you can see, there are a lot of rules and a lot of things to check. The Spreadsheet Calculators handle all of these considerations for you. However, just once you should try to calculate t* “manually”.

Once we’ve calculated the critical value, t*, how do we use it? We make the following comparisons,

Left Tail If the t-score < critical value (the critical value is going to be a negative numbers) then the t- score is going to be in the left red zone, and we would reject the null hypothesis. Otherwise, we fail to reject the null hypothesis. Right Tail If the t-score > critical value then the t-score is in the right red zone and we would reject the null hypothesis. Otherwise, we fail to reject the null hypothesis. Two Tail If the absolute value of the t-score > critical value, we reject the null hypothesis. Remember to first take the absolute value of the t-score before comparing it to the two-tail critical value. You do this just for the two-tail test.

Here’s a table summarizing these results:

Tail type Rule For Rejecting LT if then reject RT if then reject 2T then reject

For a complete guide on how to use the critical value for hypotheses testing, refer to the Hypotheses Test Charts on The Math Hub website under Miscellaneous.

The p-Value Method The p-Value Method works by comparing areas under the curve. It’s a little more difficult to understand why it works, but it is a lot easier to use than the critical value method. Consider a right-tail test and a confidence level of 95%. The area under the right tail is 0.05, which is the value of the significance. This is the red zone. If we find that the area to the right of our calculated t score is less than then that the t-score has to be in the red zone. Look at the chart of the Right-Tail Test above and think about this. This area to the right (or left in a Left-Tail Test) of our calculated t-score is called the p-Value. The rule for rejecting the null hypothesis is very simple, because there is only one rule, regardless of the type of tail test.

If p-Value then Reject the Null Hypothesis, otherwise, Fail to Reject it. Remember this rule. Tattoo it on your arm if you have to. We find the p-Value with Excel. t is the calculated t-score and df are the degrees of freedom: Left Tail Test p-Value = T.DIST(t, df) Right Tail Test p-Value = T.DIST.RT(t, df) Two Tail Test p-Value = T.DIST.2T(df)

Notice the absolute value brackets around t. That’s because T.DIST.2T only works with positive values.

As with the critical value, the Spreadsheet Calculators below handle the details for you.

Spreadsheet Calculators The following Spreadsheet Calculators can be used to perform all of your necessary calculations to do One Sample Testing of Means. Note, the shaded cells cannot be edited. Just double click on the table and it will open an Excel spreadsheet. Given The t-statistic, Find The pValue Some homework problems just give you the test statistic to work with, so use these calculators.

Most of the homework problems give you Left-Tail

Right-Tail

Two-Tail

Worked Example Let’s say that we work for the Coca-Cola Company, and it’s our job to verify that, on average, the cans of coke going out the door contain 12 oz. This is a two-tail test because, on one hand we don’t want the cans to contain less than 12 oz because then we can be accused of false labeling. On the other hand, we don’t want them to contain more than 12 oz, because, while nobody is likely to complain, we would be giving product away for free. We collect a simple random sample of 20 cans and calculate the following statistics,

We’ll use a 95% confidence level for our test. Hypotheses Statement Calculated t score

Critical Value and p-Value Here’s a spreadsheet for calculating both the critical value and the p-Value. Click on the values for t, t critical value and pValue to see how these were calculated. Note that we are using the absolute value when calculating the t score because this is a two-tail test.

Here’s a subtle point concerning the p-Value of a two tail test. The p-Value is the sum of the areas under both tails. This is the value we compare to which is the sum of the two red zones. The spreadsheet calculators handle this for you. Result Critical Value Method (the critical value), therefore fail to reject the Null Hypothesis. p-Value Method p-Value therefore fail to reject the Null Hypothesis Conclusion On the basis of our evidence, we cannot reject the claim that the cans of Coke contain, on average, 12 oz of Coca-Cola.

If you look under Miscellaneous on the website, Hypotheses Testing Chart SSM is a wonderful summary of this Unit.

Now, here’s an opportunity for you to try your hand at using the Spreadsheet Calculators.

Question #2 A thermometer should read when placed into ice water. You receive in a large batch of thermometers and you wish to verify that they do indeed have an average reading of when placed into ice water. The following is the results of your testing:

Would you accept this batch or reject it? As part of your answer, give the pValue and your reasons for either rejecting or failing to reject the claim.

This is the end of Unit 24. In class, you will get more practice with these concepts. by working exercises in MyMathLab.