Graphing Investigation - Reflect and Apply

Name:______Date:______Period:______

Graphing Investigation - Reflect and Apply:

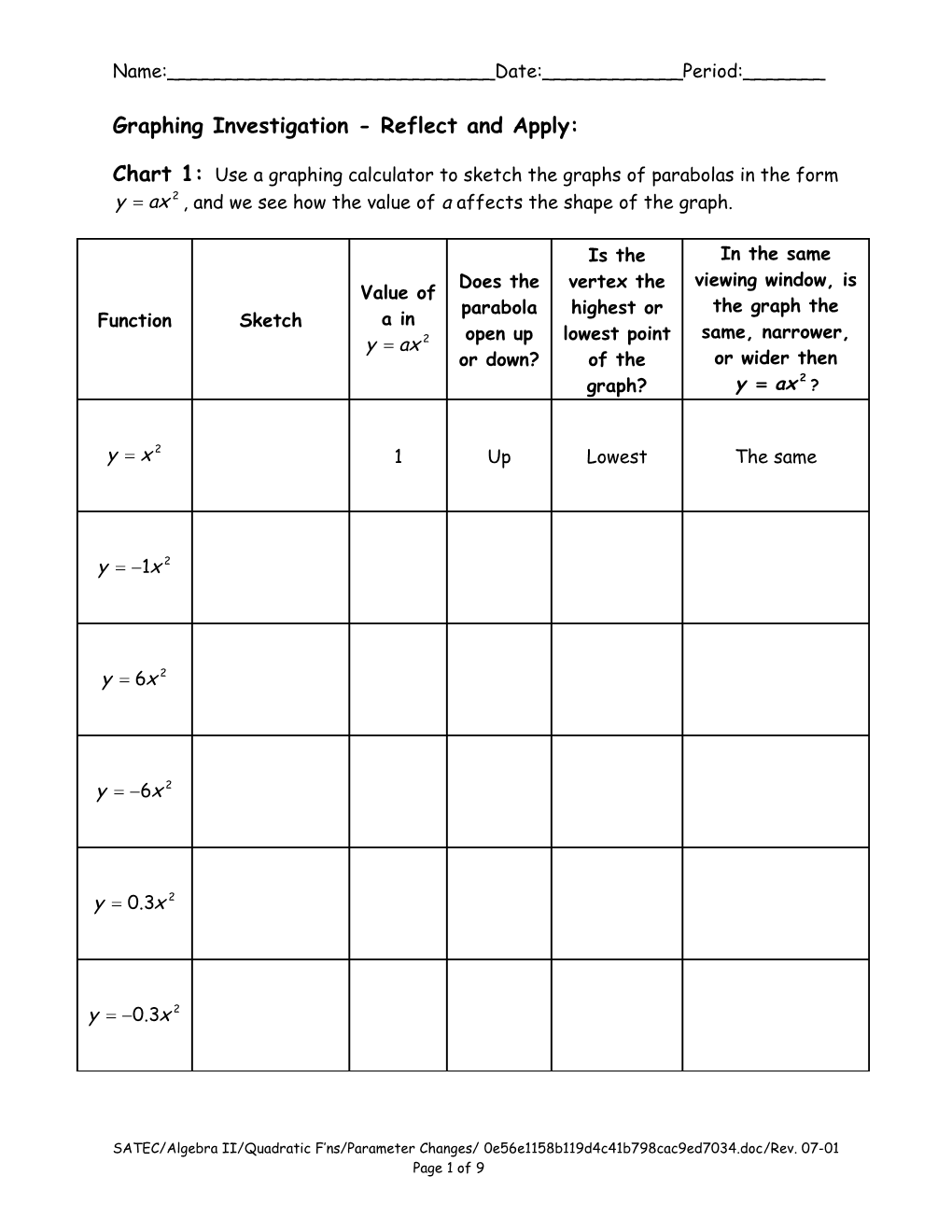
Chart 1: Use a graphing calculator to sketch the graphs of parabolas in the form y ax 2 , and we see how the value of a affects the shape of the graph.

Is the In the same Does the vertex the viewing window, is Value of parabola highest or the graph the Function Sketch a in open up lowest point same, narrower, y ax 2 or down? of the or wider then 2 graph? y ax ?

y x 2 1 Up Lowest The same

y 1 x 2

y 6 x 2

y 6 x 2

y 0.3 x 2

y 0.3 x 2

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 1 of 9 Use the information from CHART 1 to help you answer the following questions:

1. Does changing the value of a in the general equation y  ax 2 affect whether the

parabola opens up or down? If so, how?

2. Does changing the value of a affect the location of the vertex? If so, how?

3. How does the value of a indicate when the vertex is the highest point or lowest

point of the parabola?

4. Does the value of a indicate whether the parabola is narrower or wider than the

graph y  x 2 or y  1x 2 ? If so, how?

CHART 2: Use a graphing calculator to sketch the graphs of parabolas in the form y ax2  c , and we see how the value of c affects the graph.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 2 of 9 Compared to Does the y 1 x 2 , is Value of c Coordinates parabola this graph the Function Sketch in of the 2 open up same, y ax  c vertex or down? narrower, or wider?

y1 x 2  0

y1 x 2  2

y1 x 2  4

y1 x 2  8.5

Use the information from CHART 2 to help you answer the following questions: SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 3 of 9 5. How does changing the value of c affect the graphs in the chart?

6. Does changing the value of c change the location of the vertex of the parabola?

If so, in what way?

7. If c is greater than 0, what happens to the graph?

8. If c is less than 0, what happens to the graph?

9. Make up an equation whose graph will be a parabola between the graphs of the

equations y  1x 2 and y  1x 2  9 .

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 4 of 9 Graph each function on your calculator and answer the questions about it on this paper:

1. f(x) = -2(x + 4)2 + 1 a. The graph of the function is concave ______and therefore it has a

______.

b. Identify the coordinate of the vertex

c. Since the function is no longer at the origin, describe in words its location in

terms of the origin. Be specific.

d. Simplify the equation so that it is in the form f(x) = ax2 + bx + c. Show your

steps below.

2. f(x) = 3(x - 1)2 – 4

a. The graph of the function is concave ______and therefore it

has a ______.

b. Identify the coordinate of the vertex

steps below.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 5 of 9 e.

3. f(x) = 2(x - 3)2 - 5 a. The graph of the function is concave ______and therefore it

has a ______

b. Identify the coordinates of the vertex:

steps below.

4. f(x) = 5(x - 3)2 – 2

has a ______.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 6 of 9 d. Simplify the equation so that it is in the form f(x) = ax2 + bx + c. Show

your steps below.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 7 of 9 5. f(x) = (1/2)(x - 2)2 – 5 a. The graph of the function is concave ______and therefore it

has a ______.

d. Simplify the equation so that it is in the form f(x) = ax2 + bx + c. Show

your steps below.

6. f(x) = -0.4(x + 3)2 – 1

has a ______.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 8 of 9 d. Simplify the equation so that it is in the form f(x) = ax2 + bx + c. Show your steps below.

SATEC/Algebra II/Quadratic F’ns/Parameter Changes/ 0e56e1158b119d4c41b798cac9ed7034.doc/Rev. 07-01 Page 9 of 9