Chapter 8: Populations, Samples, and Probability

Witte & Witte, 9e Page 1 of 3 Pages Chapter 9 Chapter 9: Sampling Distribution of the Mean

Exercise 1

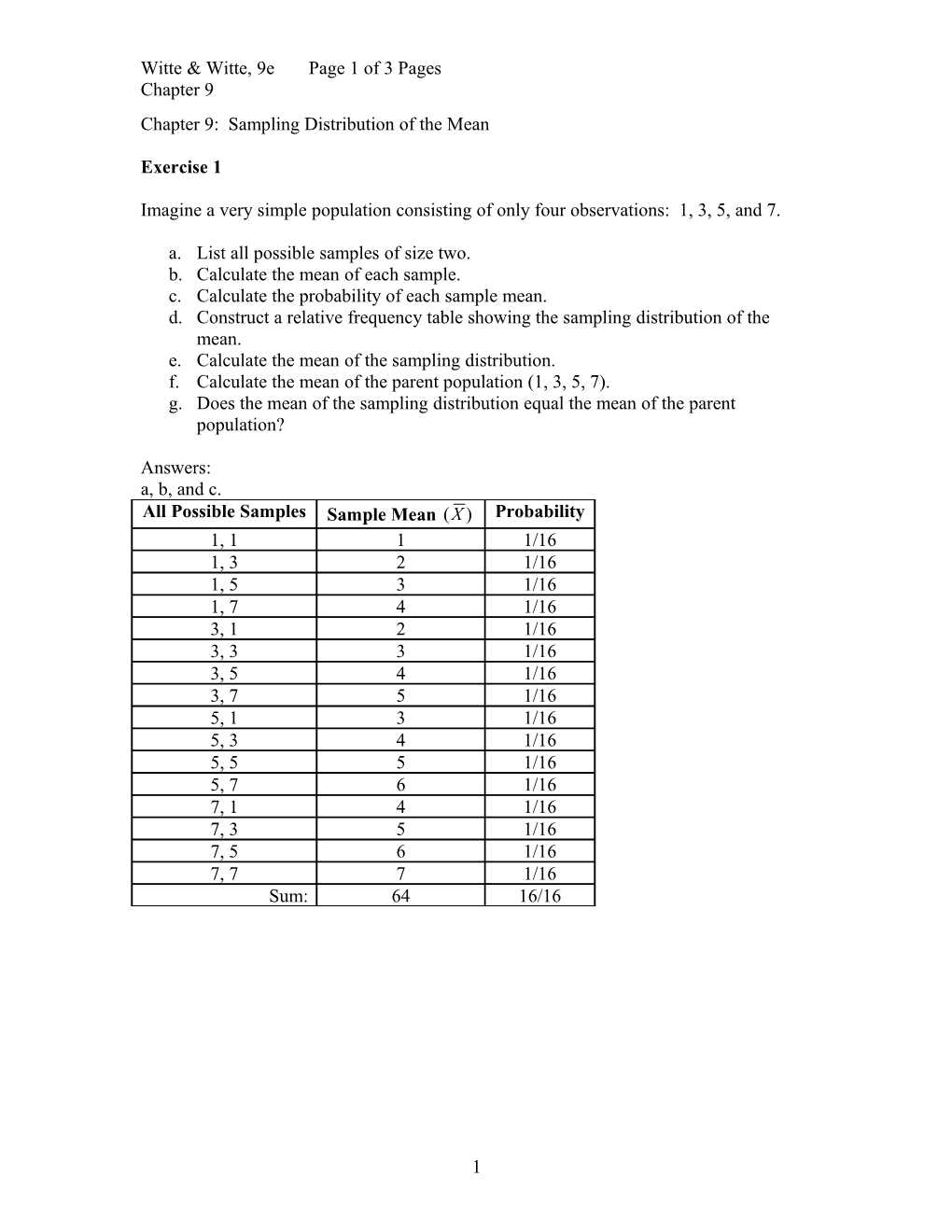
Imagine a very simple population consisting of only four observations: 1, 3, 5, and 7.

a. List all possible samples of size two. b. Calculate the mean of each sample. c. Calculate the probability of each sample mean. d. Construct a relative frequency table showing the sampling distribution of the mean. e. Calculate the mean of the sampling distribution. f. Calculate the mean of the parent population (1, 3, 5, 7). g. Does the mean of the sampling distribution equal the mean of the parent population?

Answers: a, b, and c. All Possible Samples Sample Mean (X ) Probability 1, 1 1 1/16 1, 3 2 1/16 1, 5 3 1/16 1, 7 4 1/16 3, 1 2 1/16 3, 3 3 1/16 3, 5 4 1/16 3, 7 5 1/16 5, 1 3 1/16 5, 3 4 1/16 5, 5 5 1/16 5, 7 6 1/16 7, 1 4 1/16 7, 3 5 1/16 7, 5 6 1/16 7, 7 7 1/16 Sum: 64 16/16

1 Witte & Witte, 9e Page 2 of 3 Pages Chapter 9 d. Sample Mean (X ) Probability 7 1/16 6 2/16 5 3/16 4 4/16 3 3/16 2 2/16 1 1/16

e. 64 ÷16 = 4 f. 16 ÷ 4 = 4 g. Yes, they are both equal to 4.

Exercise 2

The variance of the parent population in Exercise 1 is calculated using formula 4.5 on page 85 of your textbook. The variance of this population is equal to 5, and the standard deviation is 5  2.2361.

a. Calculate the standard error of the mean for the problem presented in Exercise 1. b. What is the symbol for the variance of the parent population? c. What is the symbol for the standard deviation of the parent population? d. What is the symbol for the standard error of the mean? e. What is the symbol for the mean of the sample means?

Answers: a. 2.2361 ÷ 2 = 1.5812 b. 2 c.  d.  X e.  X

Exercise 3

1. Calculate the standard error of the mean for the following combinations of population standard deviation and sample size.

a.  = 10, n = 9 b.  = 10, n = 25 c.  = 10, n = 100 d.  = 10, n = 225

Answers:

2 Witte & Witte, 9e Page 3 of 3 Pages Chapter 9 a. 3.33 b. 2 c. 1 d. 0.67

2. If the population standard deviation is held constant and sample size is increased, what happens to the standard error of the mean?

Answer: It decreases

Exercise 4

a. A population has a mean  = 50 and a standard deviation  = 10. If Jane generates all possible samples of size 25 from this population, the mean of the sampling distribution will equal __ and the standard error of the mean will equal __.

b. A population has a mean  = 100 and a standard deviation  = 15. If Marty generates all possible samples of size 36 from this population, the mean of the sampling distribution will equal __ and the standard error of the mean will equal __.

c. The standard error of the mean is another expression for the standard deviation of the parent population. True or False

d. The standard error of the mean is another expression for the standard deviation of the sampling distribution of the mean. True or False.

e. The central limit theorem states the sampling distribution of the mean will approximate a normal curve if the population size is sufficiently large.

Answers: a. 50, 2 b. 100, 2.5 c. False d. True e. False