Single and Double Slit Experiment

Andrew Kim, Ethan Gale, and Andrew Palm

Department of Physics and Astronomy, Augustana College, Rock Island, IL 61201

Abstract: The purpose of these two experiments is to see how well the intensity graphs fit with the theoretical model, in order to show the dualistic nature of light as existing as a wave and particle. The overall objective of the single slit experiment was to find a well fitting calculated wavelength fit over the actual wavelength, in order to develop a accurate double slit experiment. The single slit find the accuracy of the wavelength, and the double slit shows a more complicated interaction, which mathematically is a diffraction pattern superimposed on top of a intensity graph. We found that the error in wavelength to be 6% to 11%, which is greater than any single value of uncertainty. The graph we modeled was off

I. Introduction

The purpose of the single and double slit experiment is to show the particle-wavelike behavior of light. In earlier physics, light was always treated as waves, the thought of light as a particle was not treated with the same respect. However, this simple experiment shows that light are not simply waves, but the property of its fundamental being is composed of a dual relationship of its wave nature and particle nature. This changed perception encouraged modern scientists to think about light as particles, and was critical for Quantum, which eventually gave way to our nuclear age.

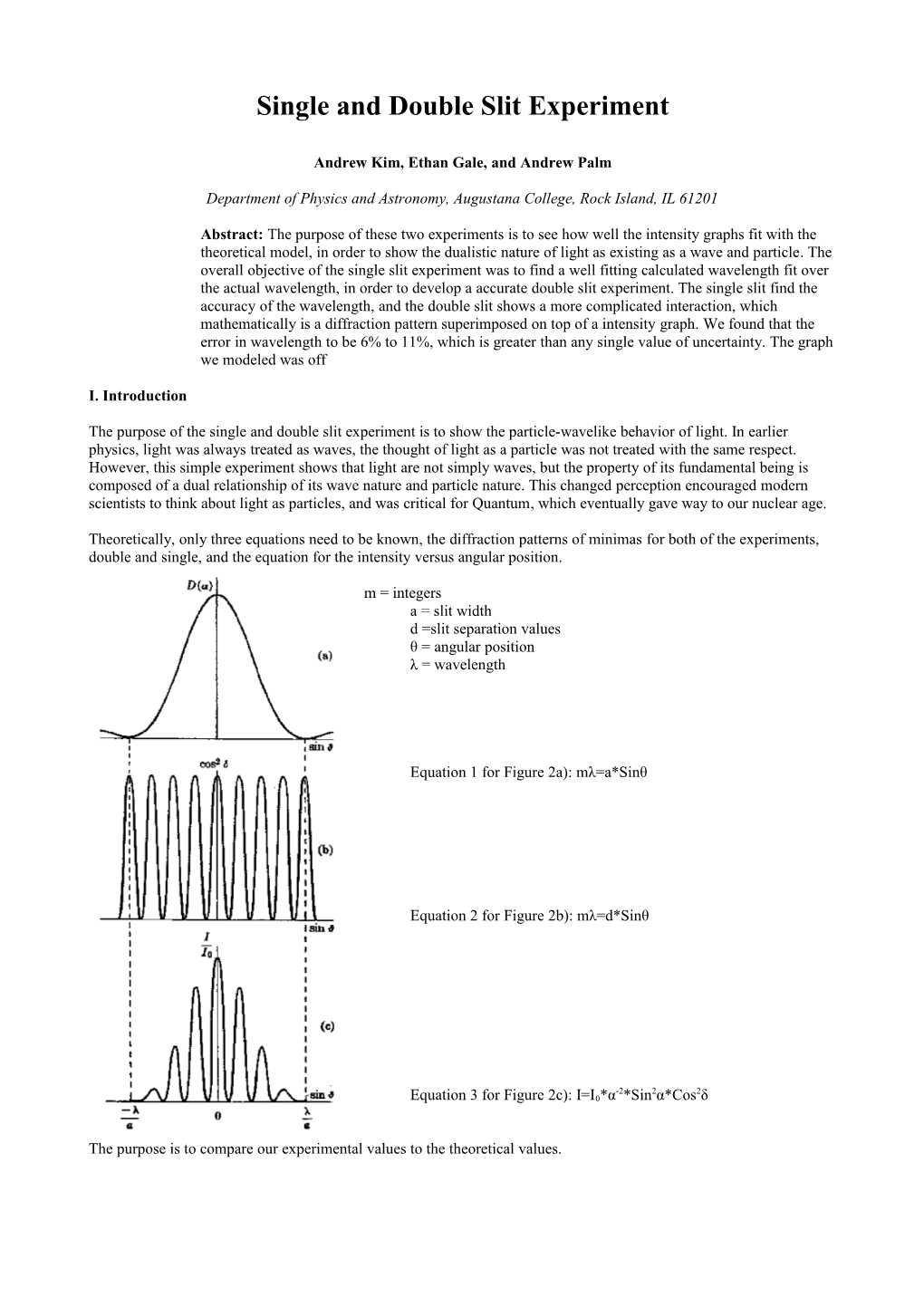
Theoretically, only three equations need to be known, the diffraction patterns of minimas for both of the experiments, double and single, and the equation for the intensity versus angular position.

m = integers a = slit width d =slit separation values θ = angular position λ = wavelength

Equation 1 for Figure 2a): mλ=a*Sinθ

Equation 2 for Figure 2b): mλ=d*Sinθ

-2 2 2 Equation 3 for Figure 2c): I=I0*α *Sin α*Cos δ

The purpose is to compare our experimental values to the theoretical values. II. Experimental Setup

This is the abstract setup of the lab. In our experiment, the laser, different slits, and screens are placed on a table. The screen is actually a detector that captures the intensity of the light of the screen. In order to make precise measurements of the diffraction pattern, the sensor needs to only receive a sliver of the pattern, so a slits are also placed on it, because if too much lights gets in then the measurements are murky, and if too much light gets blocked then the measurements become nothing. The method to receive the perfect amount of light is just eyeballing a good fit. In addition, the sensor lies on a slide where gears are turned that record the ‘angular position’ of the sensor. However, this is not truly angular position, since it doesn’t actually know the length of the slits away from the screen, so calibration is needed in order to convert this angular position into meters. This calibration can be easily done by taking a ruler, measuring how far it moves in meters than compare it to the amount of angular position change. The math should be done in order to convert the angular position into meters. From there trigonometry can be done to find Sinθ for the diffraction patterns.

We made the length apart from the slit and screen, L, to be 1m, so measurements can be done much more easily. The length of the slits and separation distances are given. We used 5% uncertainties for the givens, since they are from a machine, and ±.01 unit error for most of our measurements, since that seemed to be the smallest increment that could be measured.

Another problem existed in our setup, the laser, slit, and screens are not aligned.

Alignment procedure: In order to align the laser beam to the slit and we used straight edges and plumb bobs to estimate where the measurements lay on the ruler. We used right edge protractors to assure that the ruling sticks were perpendicular and would rest the slit, and screen flush against the ruling stick. We assumed that the table was perfectly rectangular and had parallel sides.

Data collection is simple after alignment and calibration. We needed a dark environment, so the sensor could make measurements, and essentially let data studio handle the bulk of collection. Graphs can be made by dragging two dimensions together, we wanted to drag intensities to angular position, to get intensity versus angular position graphs.

III. Results

The percent error of our experimental wavelength, ranged from 6.23% to 11.54%.

This data table shows the data points used to create our Intensity versus angular distance plot. This was graphed against equation 3.

Ruler measurements had error of ± .01m Slit width had an error of ±.002mm Slit separation had an error of ±.00625mm Calibration of Angular Position to Meters has error of ±.1 Angular Position to m Intensity had an error of ± .05 units. Graphs

This graph had the points from the second table graphed, which were the points taken at maximas. Equation 3 was modeled on top of the data points in order to show how well the fit was. The model, did not have a conceivable way of fitting the theory to the line, but you can see a particular closeness. However, our wavelength results were off by 6.23% at the least so it

Error Analysis When we had aligned the slits and screen, something must have been off. In addition, we assumed that the table was perfectly perpendicular, and that the meter sticks were straight edge. As you may know a lot of the longer meter sticks have been bending. Also, it was hard to make the screen flush with the meter stick, since the screen was bent out of shape. But, when we did the method the first time our error in wavelength was within acceptance of 5%. So, the second time we aligned we must have been a bit sloppier.

IV. Discussion Our error of wavelength, were outside the acceptable region of 5%. This was due to mostly bad procedures of alignment. However a general trend could be followed, because the plot of our intensities seemed a bit more stretched than the theoretical model of intensity versus angular position, which is good. Nonetheless, we had no means to measure the error in one graph to another, so a number cannot be assigned to how well the fit is, only visually can we really see the relationship. Overall, I would conceive that our results are partially reliable, but conclusions of the theory can still be seen.