Supplemental Section: Trigonometry

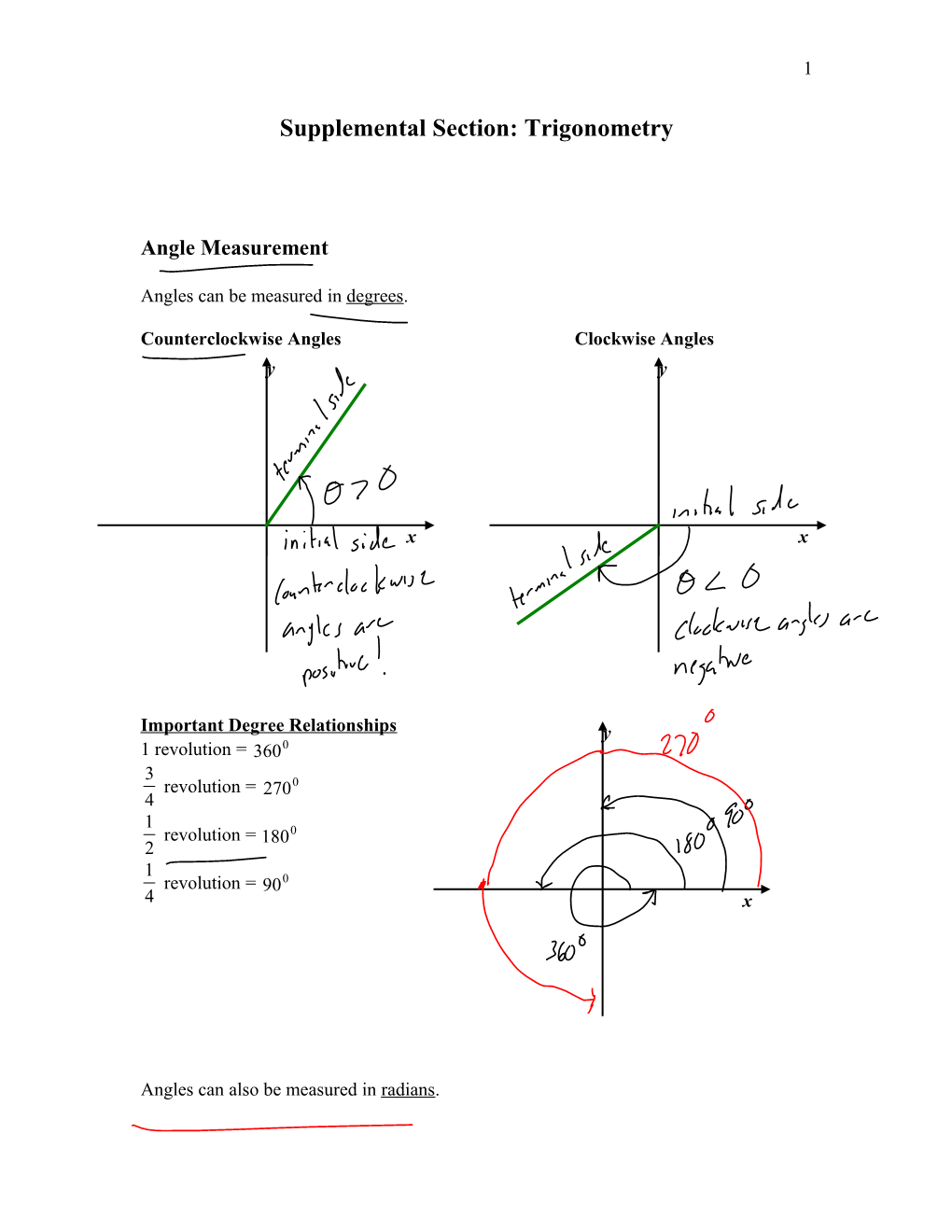
Angle Measurement

Angles can be measured in degrees.

Counterclockwise Angles Clockwise Angles y y

Important Degree Relationships y 1 revolution = 3600 3 revolution = 2700 4 1 revolution = 1800 2 1 revolution = 900 4 x

Angles can also be measured in radians. 2

Consider the unit circle y

Important Radian Relationships y 1 revolution = 2 radians 3 3 revolution = radians 4 2 1 revolution =  radians 2 1  revolution = radians 4 2 x 3

Example 1: Draw, in standard position, the angle 3300

Solution:

5 Example 2: Draw, in standard position, the angle . 4

Solution:

Angle Measurement Conversions

Formula for converting from degree to radian measure

   Radian measure  (Degree measure)  180 

Formula for converting from degree to radian measure

180  Degree measure  (Radian measure)    

Example 3: Convert 1200 from degrees to radians.

Solution:

7 Example 4: Convert  from radians to degrees. 3

Solution: Using the formula 180  Degree measure  (Radian measure)     we obtain the result

7 180  1260 Degree measure         4200 3    3

█ 5 6

The Sine and Cosine Functions

We can define the cosine and sine of an angle  in radians, denoted as cos and sin , as the x and y coordinates respectively of a point P on the unit circle that is determined by the angle  .

Consider the unit circle y

Sine and Cosine of Basic Angle Values

 Degrees  Radians cos sin 0 0 30  6 45  4 60  3 90  2 180  270 3 2 360 2 7

Note: If we know the cosine and sine values for an angle  in the first quadrant, we can determine the sine and cosine of related angles in other quadrants.

Sign Diagram for Cosine and Sine Values

4 Example 5: Compute the exact values of the sine and cosine for the angle 3

Solution:

11 Example 6: Compute the exact values of the sine and cosine for the angle . 4

Solution:

Other Trigonometric Functions

Tangent: tan  Secant: sec 

Cosecant: csc  Cotangent: cot 

11 Example 7: Find the exact values of the six trigonometric functions for the angle . 6

Solution:

█ 10 11

Note: sin 2   (sin )2 , cos2   (cos )2

Basic Trigonometric Identities

Pythagorean Identities Double Angle Formula 1. sin 2   cos2   1 sin 2  2sin cos 2. tan 2  1  sec2  3. cot 2  1  csc2 

Example 8: Find the values of x in the interval [0,2 ] that satisfy the equation sin 2x  sin x .

Solution: We solve the equation using the following steps:

sin 2x  sin x 2sin x cos x  sin x (Re place left hand side with sin 2x  2sin x cos x) 2sin x cos x  sin x  0 (Subtract sin x from both sides) sin x(2cos x  1)  0 (Factor sin x) sin x  0, 2cos x  1  0 (Set each factor equal to zero) sin x  0, 2cos x  1 (Solve for cos x) 1 sin x  0, cos x  2

1 In the interval [0,2 ], sin x  0 when x  0,  , 2 . In the interval [0,2 ], cos x  when 2  5 x  , . Thus the five solutions are 3 3

 5 x  0, , , , 2 3 3

█ 12

Graphs of Sine and Cosine

Period – distance on the x axis required for a trigonometric function to repeat its output values.

The period of f (x)  sin x and f (x)  cos x is 2 .

Example 9: Graph f (x)  sin x

Solution: The graph can be plotted using the following Maple command:

> plot(sin(x), x = -4*Pi..4*Pi, y = -2..2, color = red, thickness = 2);

█ 13

Example 10: Graph f (x)  cos x

Solution: The graph can be plotted using the following Maple command:

> plot(cos(x), x = -4*Pi..4*Pi, y = -2..2, color = red, thickness = 2);

█ 14

Graph of the Tangent Function

Period of the tangent function is  radians. The vertical asymptotes of the tangent function sin x  f (x)  are the values of x where cos x  0 , that is the odd multiples of , cos x 2 3   3   , , , , . 2 2 2 2

Example 11: Graph f (x)  tan x .

Solution: The graph is given by the following:

█ 15

Practice Problems

1. Convert from degrees to radians. a. 2100 c. 90 b.  3150 d. 360

2. Convert from radians to degrees. 3 a. 4 c.  8 7 8 b.  d. 2 3

3. Draw, in standard position, the angle whose measure is given. 3 a.  3150 c.  rad 4 7 b. rad d.  3 rad 3

4. Find the exact trigonometric ratios for the angle whose radian measure is given. 3 4 a. c. 4 3 11 b.  d. 6

5. Find all values of x in the interval [0, 2 ] that satisfy the equation. a. 2cos x 1  0 b. sin 2x  cos x

Selected Answers

7 7 1. a. , b.  6 4 2. a. 7200 , b.  6300

3 2 3 2 3 3 3 3 4. a. cos   ,sin  , tan  1, sec   2 , csc  2 , cot  1 4 2 4 2 4 4 4 4 b. cos  1,sin  0 , tan  0 , sec  1, csc : undefined , cot : undefined

 5 5. x  , 3 3