Description of the Methodology of Trend Analysis of Air Quality Data

Methodology of trend analysis of air quality data Prepared by MSC-East

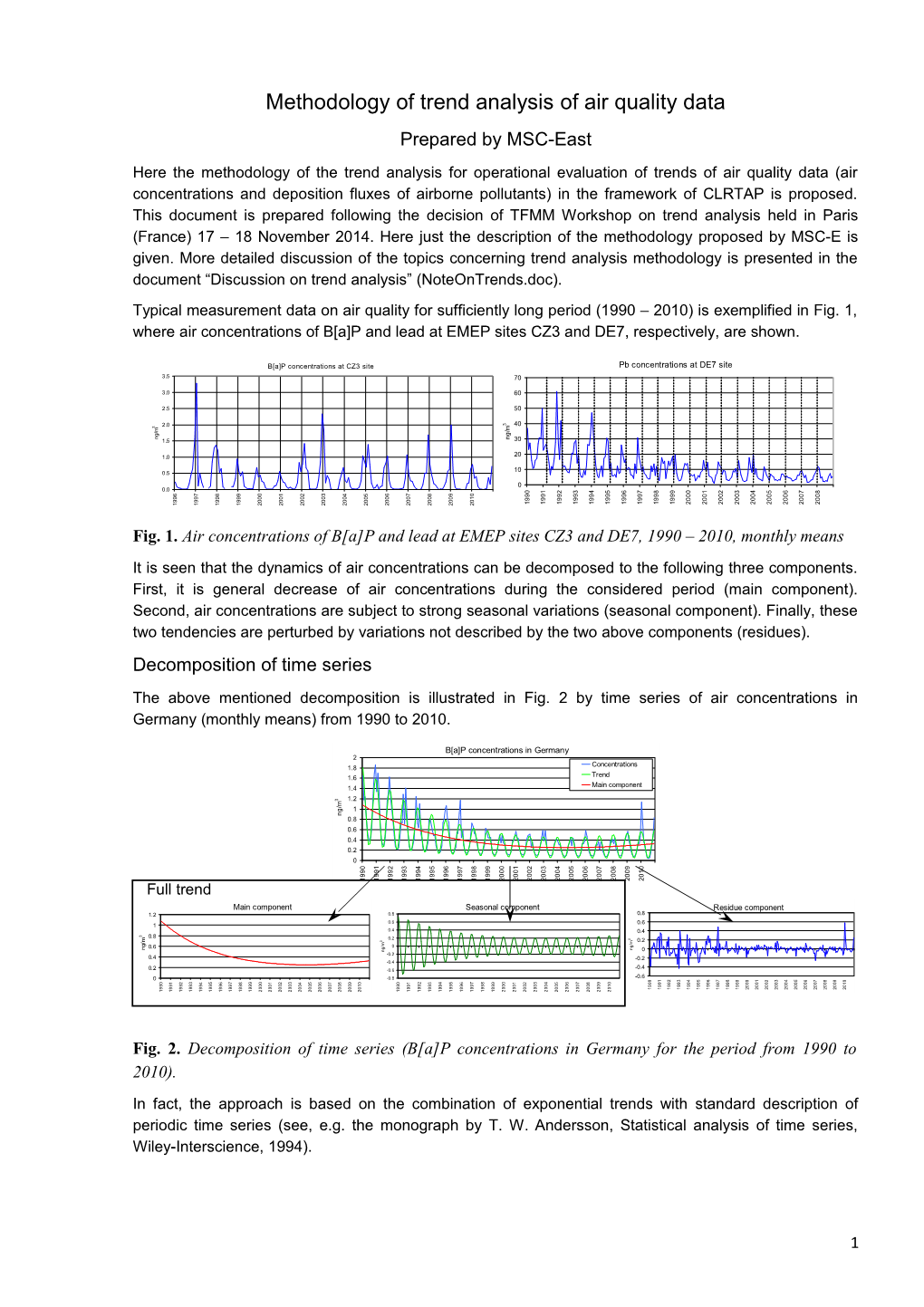
Here the methodology of the trend analysis for operational evaluation of trends of air quality data (air concentrations and deposition fluxes of airborne pollutants) in the framework of CLRTAP is proposed. This document is prepared following the decision of TFMM Workshop on trend analysis held in Paris (France) 17 – 18 November 2014. Here just the description of the methodology proposed by MSC-E is given. More detailed discussion of the topics concerning trend analysis methodology is presented in the document “Discussion on trend analysis” (NoteOnTrends.doc). Typical measurement data on air quality for sufficiently long period (1990 – 2010) is exemplified in Fig. 1, where air concentrations of B[a]P and lead at EMEP sites CZ3 and DE7, respectively, are shown.

B[a]P concentrations at CZ3 site Pb concentrations at DE7 site 3.5 70

3.0 60

2.5 50

2.0 3 40 3 m m / / g g n n 1.5 30

1.0 20

10 0.5 0 0.0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 7 0 3 6 7 9 0 6 8 9 1 2 4 5 8 9 9 9 9 9 0 0 0 9 9 9 9 9 0 0 0 0 0 0 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 0 0 0 9 9 9 9 9 0 0 0 0 0 0 9 9 9 9 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2

Fig. 1. Air concentrations of B[a]P and lead at EMEP sites CZ3 and DE7, 1990 – 2010, monthly means

It is seen that the dynamics of air concentrations can be decomposed to the following three components. First, it is general decrease of air concentrations during the considered period (main component). Second, air concentrations are subject to strong seasonal variations (seasonal component). Finally, these two tendencies are perturbed by variations not described by the two above components (residues). Decomposition of time series

The above mentioned decomposition is illustrated in Fig. 2 by time series of air concentrations in Germany (monthly means) from 1990 to 2010.

B[a]P concentrations in Germany 2 Concentrations 1.8 1.6 Trend Main component 1.4

3 1.2 m /

g 1 n 0.8 0.6 0.4 0.2 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 9 9 9 9 9 0 0 0 0 9 9 9 9 0 0 0 0 0 0 1 9 9 9 9 9 9 0 0 0 0 9 9 9 9 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 Full trend Main component Seasonal component Residue component 1.2 0.8 0.8 0.6 0.6 1 0.4 0.4

0.2 3 3 m 0.2 m / / m / g 0 g

0.6 g n n

n 0 -0.2 0.4 -0.2 -0.4 -0.4 0.2 -0.6 0 -0.8 -0.6 2 3 4 5 6 7 8 3 4 5 0 1 9 0 1 2 6 7 8 9 0 3 5 7 9 0 1 3 1 2 4 5 7 8 0 1 3 4 6 7 9 0 0 1 2 4 6 8 2 4 5 6 7 8 9 0 0 3 6 9 2 5 8 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 9 9 0 0 0 9 9 9 0 0 0 0 0 0 0 0 9 9 9 9 0 0 0 9 9 9 9 9 9 0 0 0 0 0 0 0 0 9 9 9 9 9 9 0 0 0 0 0 0 0 0 9 9 9 9 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2

Fig. 2. Decomposition of time series (B[a]P concentrations in Germany for the period from 1990 to 2010).

In fact, the approach is based on the combination of exponential trends with standard description of periodic time series (see, e.g. the monograph by T. W. Andersson, Statistical analysis of time series, Wiley-Interscience, 1994).

1 Analytically, the decomposition is described by the following formulas:

C = Cmain + Cseas + Cres, (1) where for each time t

Cmain,t = a1 · exp(- t / τ1) + a2 · exp(- t / τ2), (2) is main component,

Cseas,t = a1 · exp(- t / τ1) · (b1,1 · cos(2π · t – φ1,1) + b1,2 · cos(4π · t – φ1,2) + ...)

+ a2 · exp(- t / τ2) · (b2,1 · cos(2π · t – φ2,1) + b2,2 · cos(4π · t – φ2,2) + ...) (3) is seasonal component, and

Cres,t = Ct – Cmain,t – Cseas,t (4) are residues. Here a, b are coefficients, τ are characteristic times, and φ are phase shifts. All these parameters are calculated by the least square method. Quantification of trend

Below parameters describing the above components are described. Main component. This component is characterized by the following parameters (see Fig. 3): total reduction:

Rtot = (Cbeg – Cend) / Cbeg = 1 – Cend / Cbeg, (5) maximum and minimum annual reductions

Rmax = max Ri, Rmin = min Ri, (6) where Ri are annual reductions for year i: Ri = ΔCi / Ci = 1 – Ci+1 / Ci, and average annual reduction (geometric mean of annual reductions over all years):

1/(N–1) 1/(N–1) Rav = 1 – (Πi Ci/Ci–1) = 1 – (Cend / Cbeg) (7)

Main component 1.2 Cbeg 1

3 0.8 ΔCi m /

g 0.6 n 0.4 Cend 0.2 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2

Fig. 3. Characterization of the main component.

Seasonal component. It can be found that the amplitude of seasonal component follows the values of main component (Fig. 4a):

Seasonal component Seasonal component, normalized 0.8 100% 0.6 80% 60% 0.4 40% 0.2

3 20% m / 0 0% g n -0.2 -20% -40% -0.4 -60% -0.6 -80% -0.8 -100% 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 1 9 9 9 9 9 0 0 0 0 0 0 0 0 9 9 9 9 9 0 0 0 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 0 a 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 b 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 Fig. 4. Characterization of the seasonal component.

2 Therefore, it is reasonable to normalize values of this component by values of main component obtaining relative contribution of seasonal component to trend values (Fig. 4b). The amplitudes of the normalized seasonal component for each year can be calculated as

Ai = (max(Cseas, i / Cmain, i) – min(Cseas, i / Cmain, i)) / 2, (8) where max and min are taken within the year i. Average of these amplitudes over all years of the considered period can characterize the change of trend main component due to seasonal variations, so that the parameter quantifying seasonal variations will be: seasonal variation fraction

Fseas = , (9) where <…> stands for average value taken over all years of the considered period. Threshold value of 10% is proposed for determination whether seasonal component is essential. One more important characteristic of seasonal variations is the shift of maximum value of contamination with respect to the beginning of the year. This shift varies from year to year, and for its characterization the following parameter can be used: phase shift

S = , (10) where Si are shifts (in months) within the year i (see Fig. 5). Maximum of the trend values is searched using its analytical expression (see formulas (13) and (14)).

0.4 Phase shift 0.2 3 m / 0.0 g n Sep Oct Nov Dec Jan Feb Mar Apr May Jun -0.2 1991 -0.4 Seasonal component -0.6

Fig. 5. Definition of phase shift.

Residues. Similar to seasonal component, values of residues also follows the values of main component and they should be normalized in similar way (Fig. 6):

Residue component Random component, normalized 0.8 100% 80% 0.6 60% 0.4 40%

3 0.2 20% m /

g 0% n 0 -20% -0.2 -40% -0.4 -60% -80% -0.6 -100% 7 8 9 0 1 2 3 4 0 1 2 3 4 5 6 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 9 9 0 0 0 0 0 9 9 9 9 9 9 9 0 0 0 0 0 1 9 9 9 0 0 0 0 0 1 9 9 9 9 9 9 9 0 0 0 0 0 9 9 9 9 9 9 9 9 9 9 0 0 0 0 0 0 0 0 0 0 0 9 9 9 0 0 0 0 0 0 9 9 9 9 9 9 9 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 a b 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 Fig. 6. Characterization of residues.

So, the parameter characterizing residues can be defined as

Fres = σ(Cres,i / Cmain,i) (11) where σ stands for standard deviation over the considered period. Full list of parameters for quantification of trends is presented in Table 1:

3 Table 1. List of parameters for trend quantification

Total reduction oveк the period Rtot formula (5) Maximum annual reduction R Main component max formula (6) Minimum annual reduction Rmin

Average annual reduction Rav formula (7)

Seasonal component Relative contribution of seasonality Fseas formula (9) Shift of maximum contamination S formula (10)

Residual component Realtive contribution of residues Fres formula (11)

The example of trend evaluation (monthly averages of B[a]P concentrations in Germany in the period from 1990 to 2010) are given in Table2: Table 2. Trend evaluation (monthly averages of B[a]P concentrations in Germany in the period from 1990 to 2010)

Considered series Main component Seasonality Residues

Rtot Rav Rmax Rmin Fseas S Fres B[a]P concentrations in 70% 5% 14% –7% 75% 11.97 28% Germany, 1990 – 2010

The results show that total reduction of air concentrations over Germany within the considered period is about 70% with annual average 5% per year. In the beginning of the period annual reduction was 14%, but in the last year of the period air concentrations increased by 7%. Air contamination in Germany is subject to strong seasonal variations (around 75% of the main component). Maximum value of contamination takes place mainly in December. Fraction of contamination not explained by the constructed trend is about 30% of main component. Note. Same approach can be used for trend evaluation at the level of annual averages. In this case all parameters from Table 1 except for parameters for seasonal variations can be applied. Software for trend evaluation at monthly and annual scales will be prepared by MSC-E and made available in the nearest future.