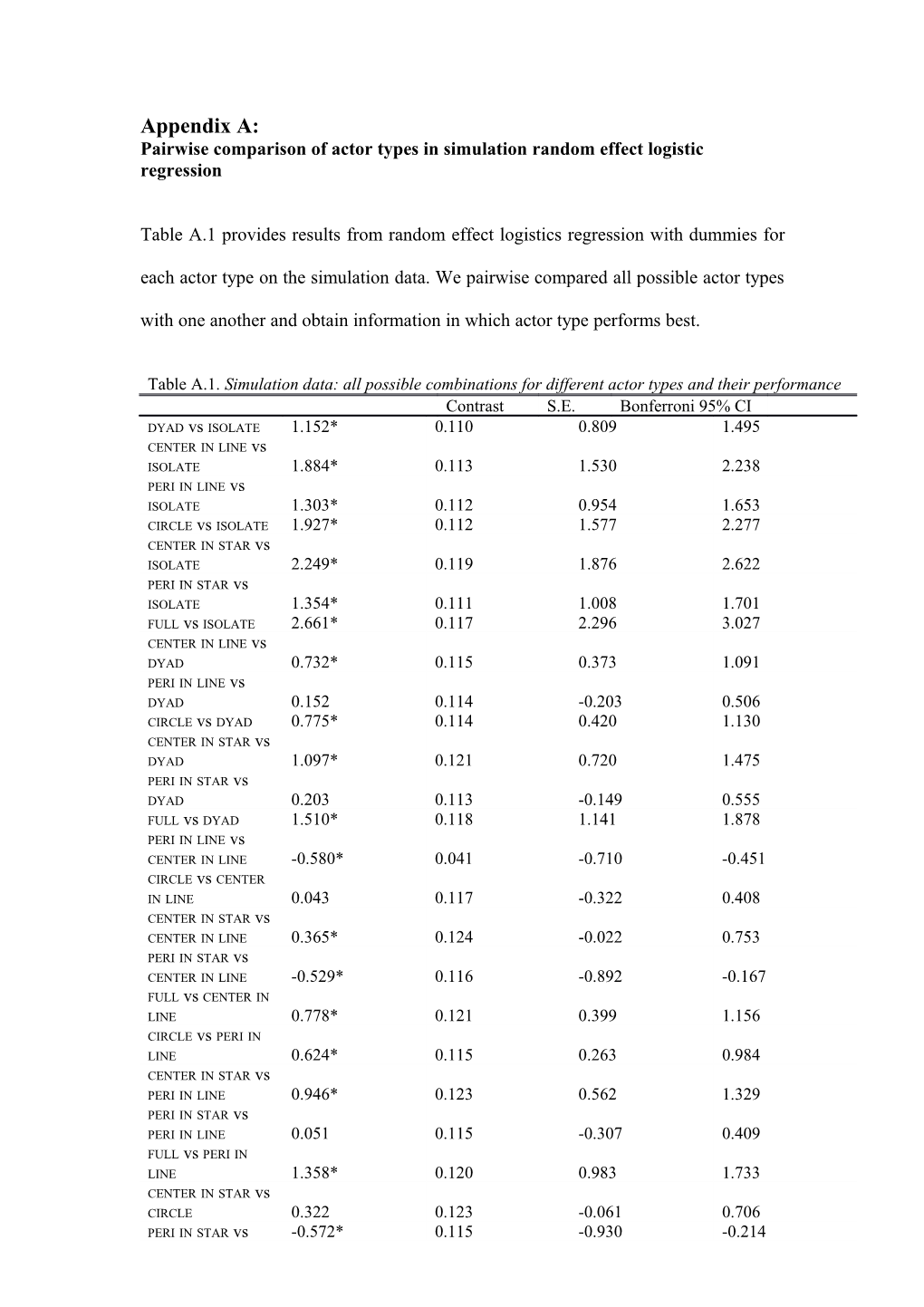
Appendix A: Pairwise comparison of actor types in simulation random effect logistic regression
Table A.1 provides results from random effect logistics regression with dummies for each actor type on the simulation data. We pairwise compared all possible actor types with one another and obtain information in which actor type performs best.
Table A.1. Simulation data: all possible combinations for different actor types and their performance Contrast S.E. Bonferroni 95% CI DYAD vs ISOLATE 1.152* 0.110 0.809 1.495 CENTER IN LINE vs ISOLATE 1.884* 0.113 1.530 2.238 PERI IN LINE vs ISOLATE 1.303* 0.112 0.954 1.653 CIRCLE vs ISOLATE 1.927* 0.112 1.577 2.277 CENTER IN STAR vs ISOLATE 2.249* 0.119 1.876 2.622 PERI IN STAR vs ISOLATE 1.354* 0.111 1.008 1.701 FULL vs ISOLATE 2.661* 0.117 2.296 3.027 CENTER IN LINE vs DYAD 0.732* 0.115 0.373 1.091 PERI IN LINE vs DYAD 0.152 0.114 -0.203 0.506 CIRCLE vs DYAD 0.775* 0.114 0.420 1.130 CENTER IN STAR vs DYAD 1.097* 0.121 0.720 1.475 PERI IN STAR vs DYAD 0.203 0.113 -0.149 0.555 FULL vs DYAD 1.510* 0.118 1.141 1.878 PERI IN LINE vs CENTER IN LINE -0.580* 0.041 -0.710 -0.451 CIRCLE vs CENTER IN LINE 0.043 0.117 -0.322 0.408 CENTER IN STAR vs CENTER IN LINE 0.365* 0.124 -0.022 0.753 PERI IN STAR vs CENTER IN LINE -0.529* 0.116 -0.892 -0.167 FULL vs CENTER IN LINE 0.778* 0.121 0.399 1.156 CIRCLE vs PERI IN LINE 0.624* 0.115 0.263 0.984 CENTER IN STAR vs PERI IN LINE 0.946* 0.123 0.562 1.329 PERI IN STAR vs PERI IN LINE 0.051 0.115 -0.307 0.409 FULL vs PERI IN LINE 1.358* 0.120 0.983 1.733 CENTER IN STAR vs CIRCLE 0.322 0.123 -0.061 0.706 PERI IN STAR vs -0.572* 0.115 -0.930 -0.214 CIRCLE FULL vs CIRCLE 0.734* 0.120 0.361 1.108 PERI IN STAR vs CENTER IN STAR -0.895* 0.053 -1.061 -0.729 FULL vs CENTER IN STAR 0.412* 0.127 0.016 0.808 FULL vs PERI IN STAR 1.307* 0.119 0.935 1.679 * = p < .05
Appendix B: Pairwise comparison of network types in simulation multilevel regression
Table B.1 provides results from a random effect generalized least regression with dummies for each network type on the simulation data. We pairwise compared all network types with one another and obtain information on which network performs best.
Table B.1. Simulation data: all possible combinations for different actor types and their performance Contrast S.E. Bonferroni 95% CI TWO DYADS vs EMPTY 0.339* 0.031 0.248 0.429 LINE vs EMPTY 0.472* 0.031 0.381 0.563 CIRCLE vs EMPTY 0.538* 0.031 0.447 0.629 STAR vs EMPTY 0.449* 0.031 0.358 0.540 COMPLETE vs EMPTY 0.608* 0.031 0.517 0.699 LINE vs TWO DYADS 0.133* 0.031 0.043 0.224 CIRCLE vs TWO DYADS 0.199* 0.031 0.109 0.290 STAR vs TWO DYADS 0.111* 0.031 0.020 0.201 COMPLETE vs TWO DYADS 0.269* 0.031 0.179 0.360 CIRCLE vs LINE 0.066 0.031 -0.025 0.157 STAR vs LINE -0.023 0.031 -0.114 0.068 COMPLETE vs 0.136* 0.031 0.045 0.227
2 LINE STAR vs CIRCLE -0.089 0.031 -0.180 0.002 COMPLETE vs CIRCLE 0.070 0.031 -0.021 0.161 COMPLETE vs STAR 0.159* 0.031 0.068 0.250 * = p < .05
Appendix C: Instructions used in the experiment
This appendix contains the written instructions that were distributed to the participants in our experiment. All subjects obtained the same English instructions.
The reader will also find screenshots in these instructions (figures 1 to 3 in the original instructions). The instructions start on the following page. Experimental Laboratory for Sociology and Economics
- Instructions - Welcome to this experiment and thank your for coming. Please read the following instructions carefully. These instructions are the same for all participants. The instructions state everything you need to know in order to participate in the experiment. If you have any questions, please raise your hand. One of the experimenters will approach you in order to answer your question.
You can earn money by means of earning points during the experiment. The number of points that you earn depends on your own choices. At the end of the experiment, the total number of points that you earn during the experiment will be exchanged at the rate of: 1000 points = 1.6 Euro The money you earn will be paid out in cash at the end of the experiment without other participants being able to see how much you earned. During the experiment you are not allowed to communicate with other participants. Please turn off your mobile phone and put it in your bag. Also, you may only use the functions on the screen that are necessary to carry out the experiment. Thank you very much.
- Overview of the session - The session consists of six parts and will last about one hour. First, there will be three practice rounds in which you can get experience with how your earnings are
4 calculated. Then, we will turn to “The Experiment”, during which you can actually earn points. Finally, you will be asked to fill out a questionnaire. Please take your time to fill in this questionnaire accurately. While you do so, your earnings will be counted. Please remain seated after having filled in the questionnaire until the payment has taken place.
- Overview of the experiment - The experiment consists of six parts each consisting of 20 rounds. In each of these rounds, you can earn points. Before a part starts, you will be randomly grouped with three other participants and you will be granted 1200 points. It will not be revealed with whom you are grouped at any moment during or after the experiment.
In each round of each part of the experiment, you will need to make a choice between four decks of cards. When you have made a choice for a deck of cards by clicking on the deck, a screen will appear in which a card is turned of this deck. This card can make you earn or lose points: your payoff. These points are added to or subtracted from your 1200 points that you were granted at the beginning of the part: your balance. You are absolutely free to switch from one deck to another any time you wish. The goal is to win as many points as possible and, if you find yourself unable to earn points make sure you avoid losing points as much as possible. The four decks of cards differ in their average value per card and the variation within the cards in a deck. Two decks have an average value of -25 points per card, while the other two have an average value of +25 points. You can thus expect to earn more if you draw cards from the latter two decks. Two decks have more variation than the other two decks. In detail, the decks have the following cards: Value -200 -100 -50 50 100 200 Average card value Variation Deck 1 3 1 2 1 1 2 -25 High Deck 2 1 4 1 2 1 1 -25 Low Deck 3 1 1 2 1 4 1 25 Low Deck 4 2 1 1 2 1 3 25 High Thus, the Deck 2 has, for example, one card with a value of -200 points and four cards with a value of -100. The cards in each deck will be shuffled and randomly placed on the positions for decks: Deck A, Deck B, Deck C, and Deck D on your screen. After every round, the card you have drawn is put back in the deck and the deck will be shuffled again. - Your neighbors - In every part of the experiment, you will be matched to three other participants. These participants also choose from Deck A, Deck B, Deck C and Deck D. The other people in your group have a deck with the same values at the same place, but the cards will be in different orders within the stacks: thus, if you have Deck 1 at the position of Deck C on your screen, the other participants in your group also have Deck 1 at the position of Deck C, but the decks of the others are shuffled differently.
Some of the other participants in your group will be your neighbors. After a round of choices, you can see these neighbors’ deck choices and what payoff this yielded them. This gives you additional information about which deck might be at which position. You can use this information for your own benefit for making further decisions. When another participant of your group is not a neighbor, a “?” is displayed on the screen and you will not know this neighbors choices and payoffs. - Explanation of the procedure within a part and the screen elements - Figure 1, figure 2, and figure 3 show the screens that you will encounter when you have to make choices. White text boxes describe how to interpret the output that is shown on your screens in the experiment. At the beginning of each part, you will see a screen similar to figure 1. You are asked to choose a deck by clicking on a deck. You will not know anything about the decks yet.
Figure 1. First choice screen and explanation The subsequent screens look like figure 2. You will see the rounds played so far and your earnings from earlier parts of the experiment combined. You will see your own payoff for the deck choice that you made: in this case Deck D, and you lost -200 points. Furthermore, the deck choices of your neighbors are shown along with their payoffs. In this example, the deck choice of neighbor P3 is Deck B and he lost -50 points with this choice. In the subsequent rounds, you will see a table so that you can keep track of your own deck choices and the payoffs that these choices have yielded you as well as deck choices of your neighbors and their associated earnings. In the first line of this table a round “0” is also displayed, where you haven’t earned anything yet, so “?” is displayed.
6 Figure 2. Subsequent screens and explanation
In the last round of a part, you will see a screen similar to figure 3. You cannot make deck choices anymore, but you will see deck choices and payoffs of yourself and your neighbors. You are asked to click “Continue” to proceed with the next part of the experiment.
Figure 3. Last screen of a part and explanation - The parts of the experiment - After every part, you will get new neighbors and the decks are randomly reordered under Deck A, B, C and D. In a new part, you cannot use the information from the previous part anymore. You will also be matched to new participants in your session and you might have a different number of neighbors. During the 20 rounds of a part, your neighbors stay the same. The first screen where you have to make a deck choice is still empty, since there are no choices made yet. After the first part of the experiment, it is displayed how many points you have earned so far. In the last round of a part, you cannot make a choice anymore and we ask you to press “Continue”. When a new part starts it will be displayed on the screen.
- End of experiment - After you have finished the questionnaire at the end of the experiment, the experimenter will approach as quickly as possible to hand over the money you earned in the experiment. Please remain seated after you have finished the questionnaire until the payment has taken place. Other participants are not able to see how much you have earned. If you have any questions, please raise your hand and the experimenter will approach. Thank you very much for participating in this experiment.
Appendix D: Order of the treatments in the experimental sessions
8 Table D.1 provides the order of the treatments in the subsequent experimental sessions. We constructed the order of the treatments so that every treatment has been at a certain place in the sequence to minimize sequence effects.
Table D.1. Order of the treatments in sessions Session Treatment orders 1 a, b, c, d, e, f 2 f*, e, d, c, b, a 3 b, d, f, a, c, e 4 e, c, a, f, d, b 5 c, a, b, e, f, d 6 d, f, e, b, a, c * = Forgone treatment due to computer crash, (a): EMPTY, (b): COMPLETE, (c): CIRCLE, (d): LINE, (e): STAR, (f): TWO DYADS
Appendix E: Correlation table of predictor variables of empirical data
Table E.1 provides the correlations between the independent variables used in the analyses of the experimental data. Table E.1. Pearson correlations between independent variables from empirical data Microlevel independent variables, N = 840 Betweenness Degree 0.430* Macrolevel independent variables, N = 210 Centralization Density -0.011 * = p < .001
10 Appendix F: Pairwise comparison of actor types in empirical random effect logistic regression
Table F.1 provides results from random effect logistics regression with dummies for each actor type on the experimental data. We pairwise compared all possible actor types with one another and obtain information in which actor type performs best.
Table F.1. Experimental data: all possible combinations for different actor types and their performance Contrast S.E. Bonferroni 95% CI DYAD vs ISOLATE 0.225* 0.064 0.025 0.425 CENTER IN LINE vs ISOLATE 0.368* 0.078 0.123 0.613 PERI IN LINE vs ISOLATE 0.087 0.076 -0.150 0.324 CIRCLE vs ISOLATE 0.536* 0.063 0.340 0.731 CENTER IN STAR vs ISOLATE 0.183 0.102 -0.137 0.503 PERI IN STAR vs ISOLATE 0.321* 0.067 0.112 0.530 FULL vs ISOLATE 0.638* 0.063 0.440 0.836 CENTER IN LINE vs DYAD 0.143 0.082 -0.112 0.398 PERI IN LINE vs DYAD -0.139 0.079 -0.387 0.109 CIRCLE vs DYAD 0.310* 0.067 0.102 0.519 CENTER IN STAR vs DYAD -0.042 0.105 -0.370 0.286 PERI IN STAR vs DYAD 0.095 0.071 -0.126 0.317 FULL vs DYAD 0.413* 0.067 0.202 0.623 PERI IN LINE vs CENTER IN LINE -0.282 0.095 -0.579 0.016 CIRCLE vs CENTER IN LINE 0.167 0.081 -0.085 0.419 CENTER IN STAR vs CENTER IN LINE -0.185 0.113 -0.539 0.169 PERI IN STAR vs CENTER IN LINE -0.047 0.085 -0.312 0.217 FULL vs CENTER IN LINE 0.270* 0.081 0.016 0.524 CIRCLE vs PERI IN LINE 0.449* 0.078 0.205 0.693 CENTER IN STAR vs PERI IN LINE 0.097 0.114 -0.259 0.452 PERI IN STAR vs PERI IN LINE 0.234 0.081 -0.020 0.488 FULL vs PERI. IN LINE 0.551* 0.079 0.305 0.797 CENTER IN STAR vs CIRCLE -0.352* 0.104 -0.678 -0.027 PERI IN STAR vs CIRCLE -0.215 0.070 -0.432 0.003 FULL vs CIRCLE 0.102 0.066 -0.104 0.309 PERI IN STAR vs CENTER IN STAR 0.138 0.110 -0.207 0.482 FULL vs CENTER IN STAR 0.455* 0.105 0.128 0.782 FULL vs PERI IN STAR 0.317* 0.070 0.098 0.537 * = p < .05
Appendix G: Pairwise comparison of network types in empirical multilevel regression
Table G.1 provides results from a random effect generalized least regression with dummies for each network type on the experimental data. We pairwise compared all network types with one another and obtain information in which network performs best.
Table G.1. Experimental data: pairwise comparison on effect of network on network performance Contrast S.E. Bonferroni 95% CI EMPTY vs CIRCLE -0.406 0.140 -0.818 0.005 COMPLETE vs CIRCLE 0.069 0.140 -0.343 0.480 LINE vs CIRCLE -0.228 0.140 -0.640 0.183 STAR vs CIRCLE -0.180 0.140 -0.591 0.232 TWO DYADS vs CIRCLE -0.244 0.147 -0.676 0.187 COMPLETE vs EMPTY 0.475* 0.140 0.064 0.887 LINE vs EMPTY 0.178 0.140 -0.233 0.590 STAR vs EMPTY 0.227 0.140 -0.185 0.638 TWO DYADS vs EMPTY 0.162 0.147 -0.270 0.594 LINE vs COMPLETE -0.297 0.140 -0.708 0.115 STAR vs COMPLETE -0.249 0.140 -0.660 0.163 TWO DYADS vs COMPLETE -0.313 0.147 -0.745 0.118 STAR vs LINE 0.048 0.140 -0.363 0.460 TWO DYADS vs LINE -0.016 0.147 -0.448 0.415 TWO DYADS vs STAR -0.065 0.147 -0.496 0.367 * = p < .05
12