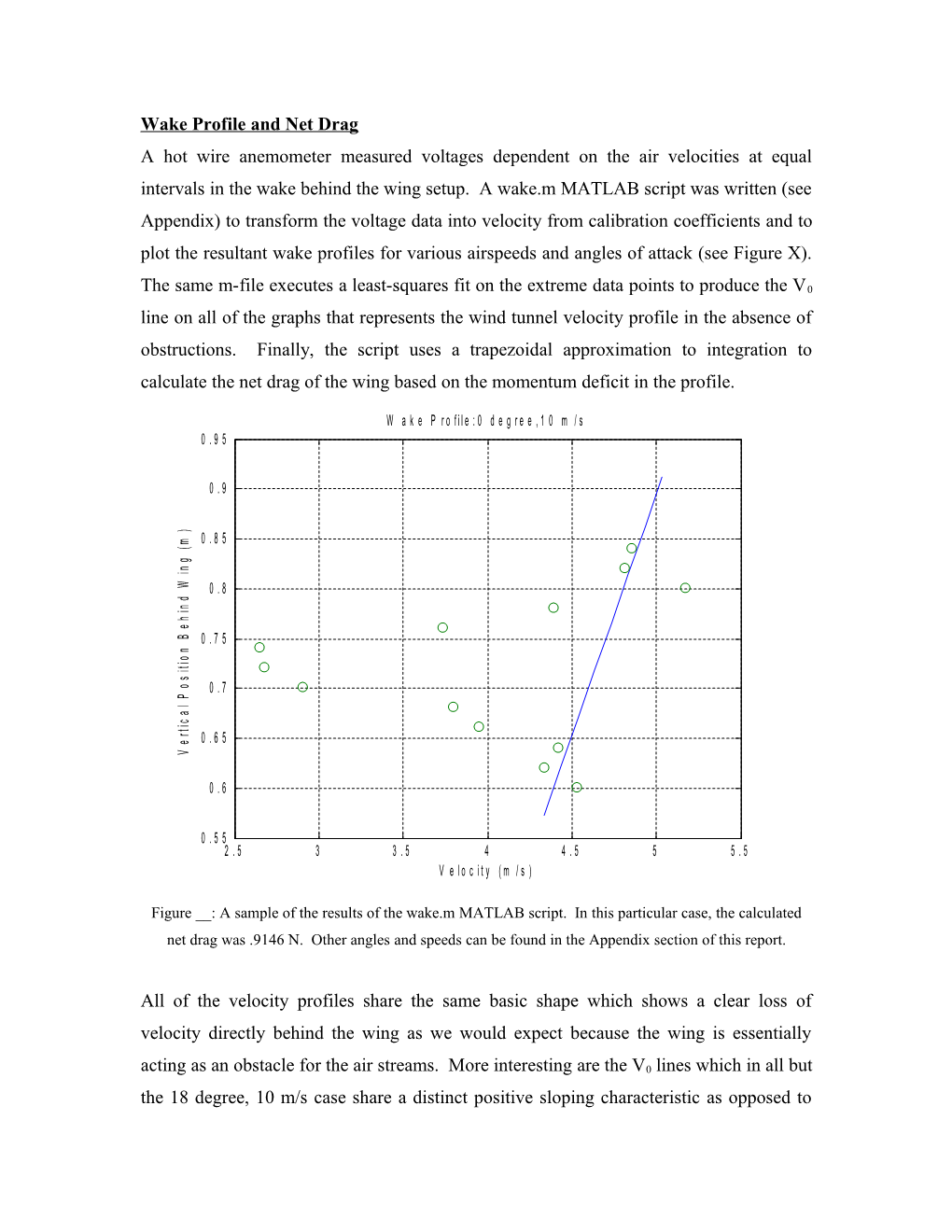
Wake Profile and Total Drag

Wake Profile and Net Drag A hot wire anemometer measured voltages dependent on the air velocities at equal intervals in the wake behind the wing setup. A wake.m MATLAB script was written (see Appendix) to transform the voltage data into velocity from calibration coefficients and to plot the resultant wake profiles for various airspeeds and angles of attack (see Figure X).

The same m-file executes a least-squares fit on the extreme data points to produce the V0 line on all of the graphs that represents the wind tunnel velocity profile in the absence of obstructions. Finally, the script uses a trapezoidal approximation to integration to calculate the net drag of the wing based on the momentum deficit in the profile.

W a k e P r o f i l e : 0 d e g r e e , 1 0 m / s 0 . 9 5

0 . 9 )

m 0 . 8 5 (

g n i W

0 . 8 d n i h e B

0 . 7 5 n o i t i s

o 0 . 7 P

l a c i t r

e 0 . 6 5 V

0 . 5 5 2 . 5 3 3 . 5 4 4 . 5 5 5 . 5 V e l o c i t y ( m / s )

Figure __: A sample of the results of the wake.m MATLAB script. In this particular case, the calculated net drag was .9146 N. Other angles and speeds can be found in the Appendix section of this report.

All of the velocity profiles share the same basic shape which shows a clear loss of velocity directly behind the wing as we would expect because the wing is essentially acting as an obstacle for the air streams. More interesting are the V0 lines which in all but the 18 degree, 10 m/s case share a distinct positive sloping characteristic as opposed to the completely vertical line of uniform velocity that we would have liked. In some cases,

V0 changes as much as 2 m/s over the course of the data taken, which is certainly nontrivial, and the variations were appropriately accounted for in drag calculations.

However, the V0 values that we are seeing in the data are consistently about half that of the values for which the wind tunnel was set for the particular trial (e.g. Figure __ from above is centered around ~5 m/s when the wind tunnel was set for 10 m/s). As a test, we gathered the readings from the pressure port on the wing that points directly upstream in the air flow. By Bernoulli’s equation, the pressure reading at a zero attack angle and the

1 incoming velocity (V ) should be related by P= r v2 . Plugging in measured values for 0 2 pressure yields the following results:

Set Velocity P = Pport1-Pstillair Measured Velocity 10 m/s 87.124 Pa 11.93 m/s 15 m/s 133.382 Pa 14.76 m/s 20 m/s 216.699 Pa 18.81 m/s Though far from perfect, these calculated values seem to be representative of the velocities that we were theoretically setting on the machine. This corroboration indicates that there is likely something askew in the calibration for the hot wire anemometer, which would throw off the drag calculations from the wake profiles.

Though the exact values of drag may not be accurate, the general trends in the drag data appear reasonable. In each separate angle category, the drag force increases with rising air speed as would be expected. Also, among non-negative angles of attack, the drag at each air speed increased with increasing angle, which makes sense because the wing presents a larger surface area when moved away from parallel. The interesting case is the negative angle of attack where the values of drag fall between the 9 and 18 degree cases. This is initially unexpected because it would seem logical that a negative 6 degree drag should be approximated by a positive 6 degree drag, but that does not match the results. The explanation is in the geometry of the wing which is not symmetrical, making the drag dependent not only on the angle away from parallel, but also on the orientation of the wing. The negative angle of attack can be expected to have higher drag than a similar positive angle because of the different way air flows over the two sides of the wing. The flowing air has more trouble staying close to the flat lower side of the wing when at a negative angle than it does staying close to the curved upper side of the wing at a positive angle. Then, for negative angles, there is a concentration of slow moving air close to the wing followed by a concentration of fast moving air, creating extremes, as opposed to more uniform distributions in the positive angle case. Though average velocity seen by the anemometer will be the same for a specific angle in positive and negative orientations, there will be higher extremes in the negative case, making the wake profile encompass a larger area. This area is what directly effects the calculation of drag.

Another consideration we thought about was the fact that the anemometer is an imperfect device for our measurements because it provides directionless quantities. We assume in all of our calculations that the velocities are all completely horizontal, which is not the case because there is certainly vertical velocity to make the air flow around the wing.