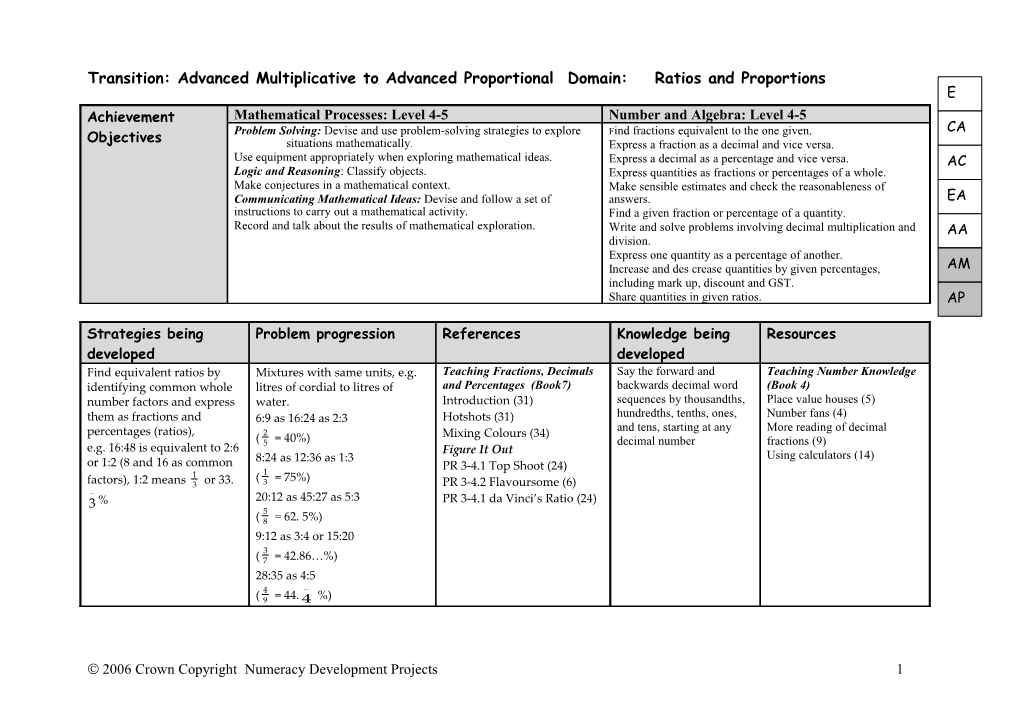
Transition: Advanced Multiplicative to Advanced Proportional

Transition: Advanced Multiplicative to Advanced Proportional Domain: Ratios and Proportions E Achievement Mathematical Processes: Level 4-5 Number and Algebra: Level 4-5 Problem Solving: Devise and use problem-solving strategies to explore Find fractions equivalent to the one given. CA Objectives situations mathematically. Express a fraction as a decimal and vice versa. Use equipment appropriately when exploring mathematical ideas. Express a decimal as a percentage and vice versa. AC Logic and Reasoning: Classify objects. Express quantities as fractions or percentages of a whole. Make conjectures in a mathematical context. Make sensible estimates and check the reasonableness of Communicating Mathematical Ideas: Devise and follow a set of answers. EA instructions to carry out a mathematical activity. Find a given fraction or percentage of a quantity. Record and talk about the results of mathematical exploration. Write and solve problems involving decimal multiplication and AA division. Express one quantity as a percentage of another. Increase and des crease quantities by given percentages, AM including mark up, discount and GST. Share quantities in given ratios. AP

Strategies being Problem progression References Knowledge being Resources developed developed Find equivalent ratios by Mixtures with same units, e.g. Teaching Fractions, Decimals Say the forward and Teaching Number Knowledge identifying common whole litres of cordial to litres of and Percentages (Book7) backwards decimal word (Book 4) number factors and express water. Introduction (31) sequences by thousandths, Place value houses (5) hundredths, tenths, ones, Number fans (4) them as fractions and 6:9 as 16:24 as 2:3 Hotshots (31) and tens, starting at any More reading of decimal percentages (ratios), 2 Mixing Colours (34) ( 5 = 40%) decimal number fractions (9) e.g. 16:48 is equivalent to 2:6 Figure It Out 8:24 as 12:36 as 1:3 Using calculators (14) or 1:2 (8 and 16 as common PR 3-4.1 Top Shoot (24) 1 ( 1 = 75%) factors), 1:2 means 3 or 33. 3 PR 3-4.2 Flavoursome (6)  3 % 20:12 as 45:27 as 5:3 PR 3-4.1 da Vinci’s Ratio (24) 5 ( 8 = 62. 5%) 9:12 as 3:4 or 15:20 3 ( 7 = 42.86…%) 28:35 as 4:5 4  ( 9 = 44. 4 %)

Strategies being Problem progression References Knowledge being Resources CA developed developed Add and subtract fractions 3 2 19 4 Teaching Fractions, Decimals Say the number one- Teaching Number Knowledge 5 + 3 = 15 = 1 15 AC and mixed numbers with and Percentages (Book7) thousandth, one-hundredth, (Book 4) 7 5 11 uncommon denominators, 8 - 12 = 24 Comparing Apples with one-tenth, one, ten etc Number fans (4) 2 3 17 5 before and after any given EA e.g. + = = 1 3 5 29 5 Apples (38) Skip counting on the number 3 4 12 12 8 + 6 = 24 = 1 24 decimal number Figure It Out line (11) 14 3 13 10 - 4 = 20 NS&AT 3-4.1 Stripping Lucky dip (13) AA 3 + 3 = 33 = 1 5 Fractions (8) 4 7 28 28 AM 7 7 56 23 3 - 11 = 33 = 1 33 Solve problems that involve 2 3 1 2 1 2 Teaching Number sense and Order fractions, decimals, Teaching Number Knowledge 1 ÷ 3 = 2 = 1 2 , 3 × 2 = 6 AP multiplying fractions and Algebraic Thinking (Book8) and percentages (Book 4) 3 4 1 3 2 6 dividing whole numbers by 1 ÷ 4 = 3 = 1 3 , 4 × 3 = 12 Harder Division of Fractions Packets of lollies (8) fractions, recognising that 3 8 2 2 3 6 (22) Rocket- where will it fit? (15) 1 ÷ 8 = 3 = 3 3 , 5 × 5 = 25 division can result in a When Small gets Bigger (24) Bead strings (17) 2 12 larger answer, 4 ÷ 3 = 2 = 6 Who has more cake (18) e.g. 4 ÷ 2 = 12 ÷ 2 = 6 3 20 2 Little halves and big quarters 3 3 3 5 ÷ 4 = 3 = 6 3 (19) 3 ÷ 3 = 24 = 8 8 3 Who wins (20) Who gets more (20) Using calculators (14) Figure It Out N 3-4.1 Waves win (8) N7/8 4.3 Awesome Athletes (13) N7/8 4.5 Gentle Giants (18)

Strategies being Problem progression References Knowledge being Resources CA developed developed Solve problems that involve 3.2 × 0.3 = 0.96 Teaching Fractions, Decimals Recall the number of tenths, Teaching Number Knowledge AC multiplying and dividing 0.72 × 8 = 5.76 and Percentages (Book7) hundredths, and one- (Book 4) Folding Fractions and thousandths in numbers of decimals using place value 0.25 × 2.4 = 0.6 Measurement and Zeros (10) Decimals (36) up to three decimal places EA estimation and conversion to 15 × 0.33 = 4.95 Tens in hundreds and more (27) Teaching Number sense and known fractions, e.g. 5.6 ÷ 0.7 = 8 1 Algebraic Thinking (Book 8) AA 0.4 × 2.8 = 1.12 (0.4< ) 4.8 ÷ 1.5 = 3.2 2 Estimation in Decimal 7.2 ÷ 0.36 = 20 8.1 ÷ 0.3 = 27 (81÷ 3 in tenths) Multiplication and Division AM 0.9 ÷ 0.03 = 30 Problems (25) __ 24 ÷ 36 = 0.66 Multiplication of Decimal AP Fractions (37) Figure It Out N 3-4.2 Spring Fever (6) N 3-4.2 Ageing in Space (8) N3-4.2 Meal Deal (9) N 3-4.3 Dog’s Dinner (14) NS@AT 3-4.2 Using Mates (16) NS&AT 3-4.2 Compatible Multiples (21) NS&AT7/8 4.2 Astronomical Proportions (16) NS 7/8 4.2 Line Up (20) N 7/8 4.5 Body Mass (10) N 7/8 4.6 Accident Prone (11)

© 2006 Crown Copyright Numeracy Development Projects 3 Transition: Advanced Multiplicative to Advanced Proportional Domain: Ratios and Proportions E Strategies being Problem progression References Knowledge being Resources CA developed developed Recall what happens when a Teaching Number Knowledge Solve problems with rates Washing cars, picking fruit Figure It Out AC using common whole 18 cars in 6 hours. NS 7/8 4.2 Fair Exchanges whole number or decimal is (Book 4) multiplied or divided by the Zap (26) number factors and How many in 15 hours? (13) power of 10 Digits on the move (29) convertion to unit rates, e.g. (18:6 as 45:15) EA NS 7/8 4.2 Energy Levels (14) Figure It Out 490 km in 14 hours is an 14:21 as 20:30 as 6:9 N 7/8 4.3 Cycling On (20) N 7/8 4.2 L Placing Points (18) average speed of 35 k/h AA 56:16 as 21:6 as 7:2 N 7/8 4.5 Dreaming of (dividing by 7 then 2). 28:12 as 49:21 as 7:3 Millions (9) 27:36 as 12:16 as 3:4 PR 3-4.1 The Caves of Koor AM PR 3-4.1 Running Hot and Cold (1) AP PR 3-4.2 Deb the Driver (2) PR 3-4.2 Pay Rates (17)

Strategies being Problem progression References Knowledge being Resources CA developed developed Combine and partition 5:6  7:12 = 12:18 = 2:3 Teaching Number sense and Rounds decimals to the nearest Teaching Number Knowledge AC 100, 10, 1, 1/ or 1/ (Book 4) ratios, and express the 9:4  7:6 = 16:10 = 8:5 Algebraic Thinking (Book 8) 10, 100 resulting ratio using Sharing in Ratios (43) e.g., rounding 5234 to nearest Sensible rounding (28) 2:3  12:11 = 14:14= 1:1 EA fractions and percentages, Ratios with Whole Numbers 100 gives 5200 e.g. Tina twice as many 8:5  7:5 = 15:10 = 3:2 (42) marbles as Ben. She has a 7:2  9:4 = 16:6 = 8:3 Figure It Out AA ratio of 2 steelies to 5 2:5  2:5  8:5 = 12:15 = PR 3-4.1 The Right Mix (22) milkies. Ben’s ratio is 3:4. 4:5 AM If they combine their 7:3  7:3  7:3  3:7 = collections what will the 24:16 = 3:2 AP ratio be? 1:3  1:3  4:5  4:5  i.e. 2:5  2:5  3:4 = 7:14 = 4:5 = 14:21 = 2:3 1:2 Find fractions between two Find fractions between: Teaching Fractions, Decimals Recall fraction  decimal  Teaching Number Knowledge 2 1 1 3 and Percentages (Book7) percentage conversions for (Book 4) given fractions using and , and , equivalence, conversion to 5 2 4 10 Feeding Pets (40) fractions in common use, e.g., Equivalent fractions, decimals 3 4 3 7 Figure It Out eighths, tenths, twentieths and percentages (21) decimals or percentages, and 4 and 5 , 5 and 12 , NS&AT 3-4.1 Fishy Fractions Difficult fractions to proximity to benchmark 5 7 7 9 and , and , (16) percentages (21) fractions, 8 12 8 10 5 6 3 4 PR 3-4.2 Just right (8) Figure It Out 1 1 3 9 2 9 19 4 and 5 , 7 and 9 , 2 2 PR 3-4.2 Fruit proportions (20) N 3-4.1 Bottle ups (10) e.g. 5 < < 3 , = 30 . 15 15 8 9 3 7 PR 3-4.2 Ratio Rip (10) NS 7/8 4.2 Pizza pieces (19) 9 and 10 , 4 and 11 . PR 3-4.2 Laser Blazer (12) N 7/8 4.5 Percentage passes (22)

Strategies being developed Problem progression References CA

Solve division problems that have fraction 1 Teaching Number sense and Algebraic Thinking 30 ÷ 4 = 7r2 or 7 2 or 7.5 AC answers and express the remainder as a __ (Book 8) 17 ÷ 3 = 5r2 or 5 2 or 5. whole number, fraction or decimal 3 66 Finding Remainders (31) EA appropriate to the problem, e.g. 19 ÷ 8 = 2r3 43 ÷ 5 = 8r3 or 8 3 or 8.6 Applying Remainders (32) 3 5 or 2 8 or 2.375. 7 157 ÷ 10 = 15r7 or 15 10 or 15.7 AA 90 ÷ 8 = 11r2 or 11 1 or 11.25 4 AM 2 __ 58 ÷ 6 = 9r4 or 9 3 or 9.66 Solve measurement problems with fractions 7 1 7 2 7 1 8 ÷ 4 = 8 ÷ 8 = 2 = 3 2 lots of one quarter. AP by using equivalence and reunitising the 4 1 8 5 8 3 whole (one), 5 ÷ 2 = 10 ÷ 10 = 5 = 1 5 3 2 9 8 9 1 9 3 18 15 18 1 e.g. 4 ÷ 3 = 12 ÷ 12 = 8 = 1 8 lots of two 10 ÷ 4 = 20 ÷ 20 = 15 = 1 5 thirds. 7 2 21 16 21 5 8 ÷ 3 = 24 ÷ 24 = 16 = 1 16 1 2 5 8 5 4 ÷ 5 = 20 ÷ 20 = 8 3 3 6 15 6 2 10 ÷ 4 = 20 ÷ 20 = 15 = 5

Strategies being developed Problem progression References CA

Estimate and find percentages of whole number 25% of 64 = 16 Teaching Number sense and Algebraic Thinking AC and decimal amounts and calculate percentages 80% of 45 = 36 (Book 8) from given amounts 35% of 24 = 8.4 Percentage Problems in Two Steps (27) EA e.g. Liam gets 35 out of 56 shots in. What 65% of 36 = 23.4 Percentage Increases and Decreases in One Step (27) Reverse Percentage Problems (44) percentage is that? 58% of 82 is about 60% of 80 = 48 (actual 47.56) Inflation (45) AA 77% of 38 is about 75% of 40 = 30 (actual 29.26) 50% on is not the Same as 50% Off! (45) 32 out of 48 is about 32 out of 50 = 64% (66.6%) GST Rules (46) AM 32 out of 39 is about 32 out of 40 = 80% (82%) Figure It Out 22 out of 29 is about 22 out of 30 which is 3 1 × 22 N 3-4.2 Flying Home (2) 3 N 7/8 4.3 Purchasing Payments (11) AP = 77% (75.8%) PR 3-4.2 Fully Grown (9)

Predict which divisions result in terminating and Find prime factors of 20, 16,25,28,15,40,18,36,70 Teaching Number sense and Algebraic Thinking non-terminating decimals using prime factors Find which divisions result in terminating and (Book 8) non terminating decimals: Recurring and Terminating Decimal Fractions (38) 1 ÷ 16 = , 1 ÷ 25 = , 1 ÷ 28 = , 1 ÷ 15 = , 1 ÷ 40 Figure It Out = , 1 ÷ 18 = , 1 ÷ 36 = , 1 ÷ 70 = . NS&AT 3-4.2 Non-stop Ninths (12)) Why do these fractions result in terminating or non-terminating decimals? __ 3 5 15 = 0.2, 15 = 0. 33 __ 9 2 18 = 0.5, 18 = 0.11

Strategies being developed Problem progression References CA

Solve percentage change problems, e.g. GST of 12.5 % has been added to these prices. Teaching Number sense and Algebraic Thinking AC The house price rises from $240,000 to $270,000. What are the nett prices? (Book 8) $ , $ , $ , 270 000 240 000 30 000 1 $81 less 12.5% is $72 Calculating Percentage Change (26) The increase is $240,000 = $240,000 = 8 = EA 1 Estimating Percentages (26) 12 $108 ($96 nett), 2 = 12.5% Figure It Out 100 $225 ($200) NS 7/8.2 Gains and Losses (21) AA $99 ($88) The house price increases. What is the percentage change? AM $125,000  $150,000 $96,000  $168,000 AP $495,000  $495,000 $333,000  $444,000 $256,000  $332,800 Solve problems with inverse rates, Building houses: Teaching Number sense and Algebraic Thinking e.g. 4 people can paint a house in 9 days. How 5 people take 4 days. How long will 2 people (Book 8) long will 3 people take to do it? take? Comparing by Finding Rates (43) It takes 36 people days to paint the house so it (10 days) Inverse Ratios (43) will take 3 people 12 days. 4 people take 7 days. How long will 14 people take? Figure It Out PR 3-4.2 Balancing Act (4) (2 days) 6 people take 6 days. How long will 8 people take? 1 (4 2 days) It takes 3 hens 4 days to lay 6 eggs. How long will it take 5 hens to lay 10 eggs? (4 days) It takes 8 workers 7 days to build 1 house. How long does it 6 workers to build 3 houses? (56