Chapter 18 Worksheet 3 G under non-standard conditions, relationship between Go and K
Consider the generalized reaction: aA + bB = cC + dD
Recall that if you mix A, B, C, and D together, you can decide which direction the reaction will proceed by comparing the reaction quotient (Q) to the equilibrium constant (K) OR by determining the sign of G.
c d c d [C] [D] [C]eq [D]eq Q a b K a b [A] [B] [A]eq [B]eq
If Q < K or G < 0 then the forward reaction is spontaneous (forward rate > reverse rate). If Q > K or G > 0 then the reverse reaction is spontaneous (forward rate < reverse rate). If Q = K or G = 0 the reaction is at equilibrium (forward rate = reverse rate).
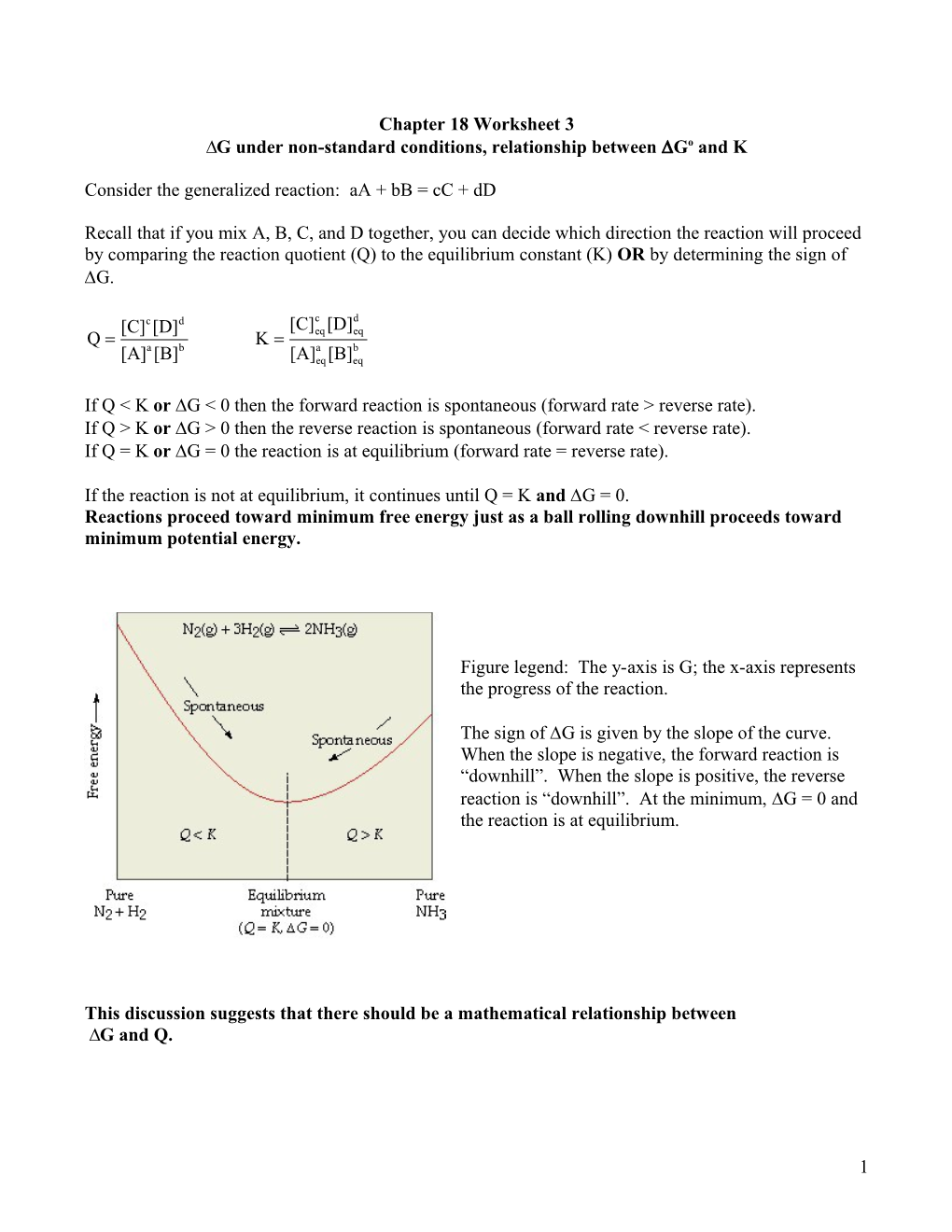
If the reaction is not at equilibrium, it continues until Q = K and G = 0. Reactions proceed toward minimum free energy just as a ball rolling downhill proceeds toward minimum potential energy.
Figure legend: The y-axis is G; the x-axis represents the progress of the reaction.
The sign of G is given by the slope of the curve. When the slope is negative, the forward reaction is “downhill”. When the slope is positive, the reverse reaction is “downhill”. At the minimum, G = 0 and the reaction is at equilibrium.
This discussion suggests that there should be a mathematical relationship between G and Q.
1 The relationship between G and Q: calculating G under non-standard conditions
G = Go + RTlnQ (When using this equation, the unit on G must be J/mol or kJ/mol)
We will not derive this equation, but we can analyze it to see that it makes sense.
1. If a reaction is set up under standard conditions what is the value of Q and G (use the equation above)?
Q = ______
G = ______
2. As Q increases, what happens to the value of G? Is this as expected?
o The relationship between G and Keq and between G and Q
3. If a reaction is at equilibrium,
Q = ______
G = ______
4. Insert the values from question 3 into the equation for G above. Rearrange the equation to produce o an expression for G . Rearrange this expression to solve for Keq.
Go = ______
eq = ______
5. Substitute your expression for Go into the original equation for G.
G = ______
If Q = Keq, what is the value of G? ______
If Q < Keq, what is the sign of G? ______
If Q > Keq, what is the sign of G? ______
2 o o Relationship between H , S , T, and Keq (expt. 12H)
Recall that: G = H – TS
Therefore: Go = Ho – TSo
From the previous page, there is a second way to calculate Go:
o G = -RTlnKeq
o Equate these two expressions for G and solve for lnKeq.
This is the equation used in experiment 12H!
A plot of lnKeq vs. 1/T produces a straight line with: slope = –Ho/R y-intercept = So/R (This is called “C” in expt. 12H)
6. According to the equation above, how does Keq depend on temperature for an endothermic or exothermic reaction?
3 7. Consider the reaction 2NO2 (g) → N2O4 (g)
a. Is this reaction spontaneous under standard conditions at 298 K? At 350 K? Answer these
questions in two ways: determine the sign of G and compare Q to Keq.
4 b. Is the reaction spontaneous at 350 K if the reaction mixture consists of 1.60 atm of NO2 and 0.40 atm of N2O4? Answer in two ways as in part a.
5 Summary
G and Q provide the same information: How far the reaction is from equilibrium and which direction the reaction must proceed in order to reach equilibrium. The further a reaction is from equilibrium, the more work it can do.
o G and Keq provide the same information: The concentrations of reactants and products present at equilibrium.
The second law of thermodynamics explains how Hrxn and Srxn determine the direction in which a reaction will proceed.
Thermodynamics explains the relationship between temperature and Keq
Thermodynamics provides a way to use calorimetry to measure equilibrium constants.
6