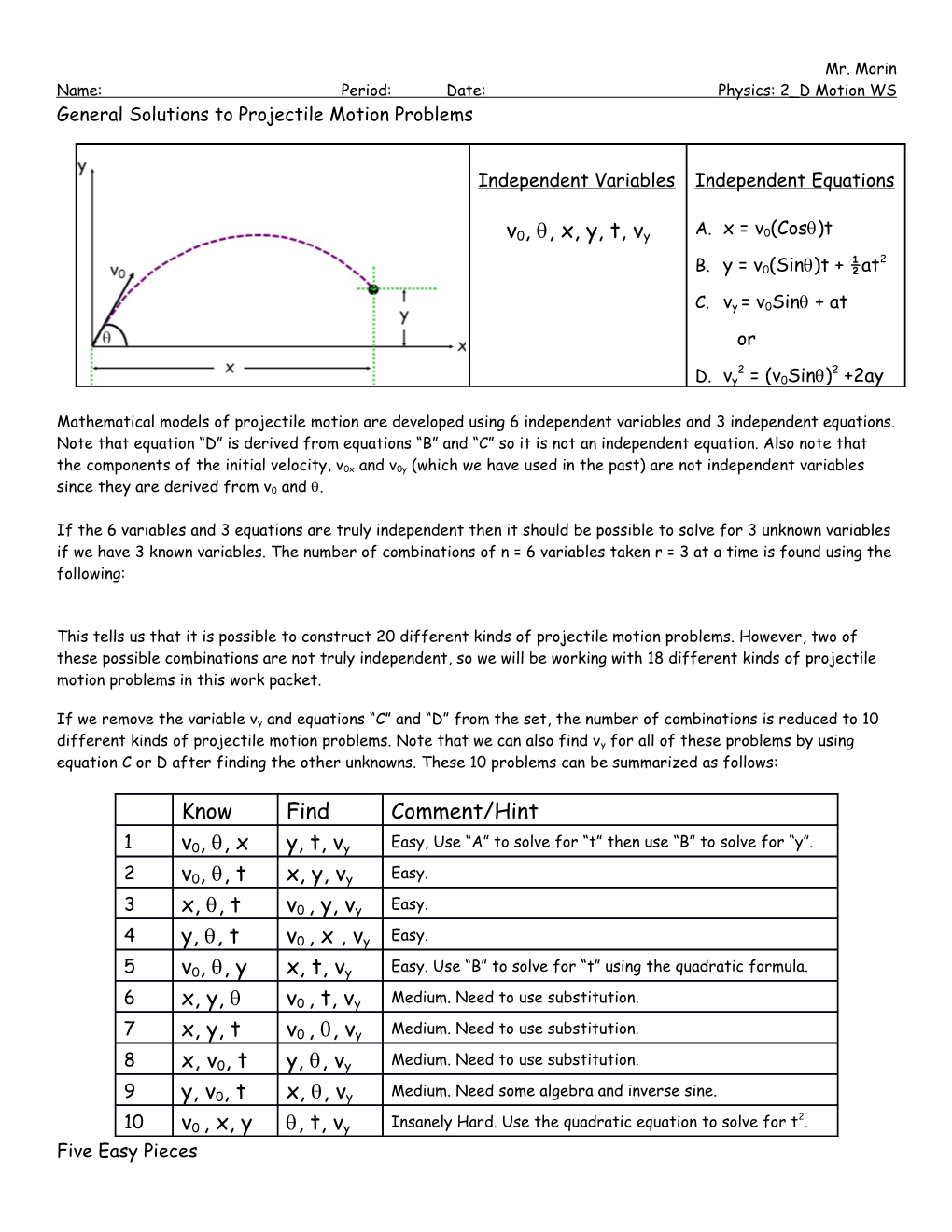
Name: Period: Date: Physics: 2 D Motion WS

Mr. Morin Name: Period: Date: Physics: 2_D Motion WS General Solutions to Projectile Motion Problems

Independent Variables Independent Equations

v0, , x, y, t, vy A. x = v0(Cos)t 2 B. y = v0(Sin)t + ½at

C. vy = v0Sin + at or

2 2 D. vy = (v0Sin) +2ay

Mathematical models of projectile motion are developed using 6 independent variables and 3 independent equations. Note that equation “D” is derived from equations “B” and “C” so it is not an independent equation. Also note that the components of the initial velocity, v0x and v0y (which we have used in the past) are not independent variables since they are derived from v0 and .

If the 6 variables and 3 equations are truly independent then it should be possible to solve for 3 unknown variables if we have 3 known variables. The number of combinations of n = 6 variables taken r = 3 at a time is found using the following:

This tells us that it is possible to construct 20 different kinds of projectile motion problems. However, two of these possible combinations are not truly independent, so we will be working with 18 different kinds of projectile motion problems in this work packet.

If we remove the variable vy and equations “C” and “D” from the set, the number of combinations is reduced to 10 different kinds of projectile motion problems. Note that we can also find vy for all of these problems by using equation C or D after finding the other unknowns. These 10 problems can be summarized as follows:

Know Find Comment/Hint

1 v0, , x y, t, vy Easy, Use “A” to solve for “t” then use “B” to solve for “y”.

2 v0, , t x, y, vy Easy.

3 x, , t v0 , y, vy Easy.

4 y, , t v0 , x , vy Easy.

5 v0, , y x, t, vy Easy. Use “B” to solve for “t” using the quadratic formula.

6 x, y,  v0 , t, vy Medium. Need to use substitution.

7 x, y, t v0 , , vy Medium. Need to use substitution.

8 x, v0, t y, , vy Medium. Need to use substitution.

9 y, v0, t x, , vy Medium. Need some algebra and inverse sine. 2 10 v0 , x, y , t, vy Insanely Hard. Use the quadratic equation to solve for t . Five Easy Pieces We will begin with 5 easy problems. Note that they may or may not be in the same order as given in the table. Also note that at the end of every problem it is possible to find the velocity, v (magnitude and direction), by using v0, , and vy with the Pythagorean theorem. Make sketches for each problem and be careful to use the correct signs.

1. You launch a projectile with an initial velocity of 4 m/s at an angle of 60° and it hits a target at a distance of 1.0 m in the horizontal direction. a. What is the “y” coordinate of the target, b. how long does it take for the projectile to hit the target, c. what is the y-component of its velocity just before it impacts the target, d. and what is its velocity … magnitude and … e. direction, just before it impacts the target.

2. You launch a projectile with an initial velocity of 4 m/s at an angle of 50° and it hits a target 0.4 s after it is launched. a. What is the “x” coordinate of the target, b. what is the “y” coordinate of the target, c. what is the y-component of its velocity just before it impacts the target, d. and what is its velocity … magnitude and … e. direction, just before it impacts the target.

3. You have calibrated your cannon, and you know that it has a muzzle velocity of 4.5 m/s. Your teacher has given you a launch angle of 40° and you need to hit a target that is 0.5 m below the muzzle of your cannon. a. At what “x” distance from your cannon should you place the target in order to hit it, b. how long does it take for the projectile to hit the target, c. what is the y-component of its velocity just before it impacts the target, d. and what is its velocity … magnitude and … e. direction, just before it impacts the target.

4. You launch a projectile with an initial velocity of at an angle of 45° and it hits a target at a level of 0.4 m above the horizontal 0.4 s after it is launched. a. What is the “x” coordinate of the target, b. what was its initial velocity, c. what is the y-component of its velocity just before it impacts the target, d. and what is its velocity … magnitude and … e. direction, just before it impacts the target.

5. You launch a projectile with an initial velocity of at an angle of 30° and it hits a target 0.4 s after it is launched at a horizontal distance of 0.4 m. a. What is the “y” coordinate of the target, b. what was its initial velocity, c. what is the y-component of its velocity just before it impacts the target, d. and what is its velocity … magnitude and … e. direction, just before it impacts the target.

Five Medium Pieces The next 5 problems are a little bit harder because you need to use algebra to find an expression for a variable from one equation, and then substitute it into another equation. Note the next 5 problems may or may not be in the same order as given in the table. Also note that at the end of every problem it is again possible to find the velocity, v (magnitude and direction), by using v0, , and vy with the Pythagorean theorem. When you come to the “insanely hard” problem, you need to derive an expression for “t” that is a 4th order polynomial. Fortunately, there is no t3 term and no t term, so the quadratic formula can be applied to solve for t2. Then take the square root to find t. Make sketches for each problem and be careful to use the correct signs.

6. You need to calibrate your giant paint ball bazooka, so you fire it at an angle of 60° and you find that the giant paint ball splatters the ground at a horizontal distance of 107 m from the end of the muzzle, and a distance of 1.7 m below the end of the muzzle.

a. What is the muzzle velocity, v0, of your giant paint ball bazooka, b. how long does it take for the giant paint ball to hit the ground and splatter, c. what is the y-component of its velocity just before it splatters, d. and what is its velocity … magnitude and … e. direction, just before it splatters.

7. You are jogging along Zuma beach when you see a flash of fire up on a cliff, and then you notice the splash of a cannon ball next to you in the ocean. You instantly estimate (from the puff of smoke) that the cannon was fired a horizontal distance of 80 m from the top of a cliff 40 m above your position. Based on your observation of the fiery explosion from the mouth of the cannon (as it was fired), you estimate that the cannon ball was in the air for 3.0 seconds. a. What was the muzzle velocity of the cannon, b. At what angle was it fired, c. what is the y-component of its velocity just before it impacts the water, d. and what is its velocity … magnitude and … e. direction, just before it impacts the water.

8. You decide to make a retaliatory gesture before retreating, so you whip out your giant paint ball bazooka and wildly shoot it in the direction of the cliff as you are scrambling to retreat. Your giant paint ball bazooka fires a giant paint ball with a muzzle velocity of 35 m/s and you notice that it hits the cliff (which is still at a horizontal distance of 80 m from your position) 3.0 seconds after you pulled the trigger. a. At what height above your giant paint ball bazooka muzzle does the giant paint ball hit the cliff, b. At what angle was it fired, c. what is the y-component of the giant paint ball’s velocity just before it impacts the cliff, d. and what is its velocity … magnitude and … e. direction, just before it impacts the cliff.

9. You decide to fire another shot from behind the safety of a big rock, so you whip out your giant paint ball bazooka and shoot it in the direction of the cliff. Your giant paint ball bazooka fires a giant paint ball with a muzzle velocity of 35 m/s and you notice that it hits the cliff at a height of 33m above the muzzle of your giant paint ball bazooka 3 seconds after you pulled the trigger. a. At what horizontal distance from the cliff did you fire the giant paint ball, b. At what angle was it fired, c. what is the y-component of the giant paint ball’s velocity just before it impacts the cliff, d. and what is its velocity … magnitude and … e. direction, just before it impacts the cliff. 10. You dart from rock to rock and crawl the last few feet to get closer to the cliff. Now you are only 60 meters from the base of the 40 m high cliff. Armed with the knowledge that your giant paint ball bazooka has a muzzle velocity of 35 m/s, and remembering the trig identity that sin2 = 1 – cos2, you do an insanely difficult calculation to find out the correct launch angle that you need to reach the top of the cliff (and give the cannon a new paint job). a. At what angle should you aim your giant paint ball bazooka, b. how long will it take for your giant paint ball to splatter the cannon on top of the cliff, c. what is the y-component of the giant paint ball’s velocity just before it impacts the cannon, d. and what is its velocity … magnitude and … e. direction, just before it impacts the cannon.