ALGEBRA REVIEW
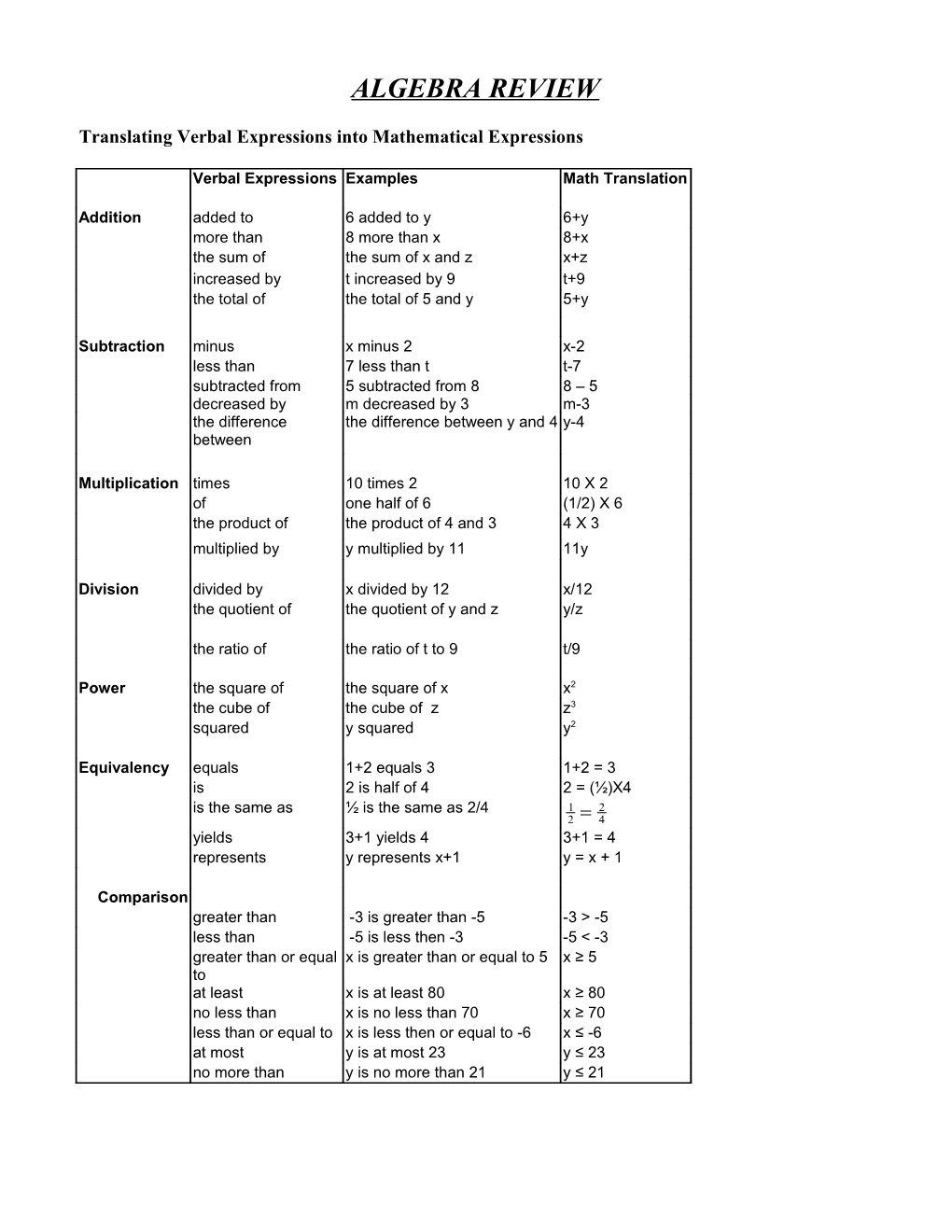
Translating Verbal Expressions into Mathematical Expressions
Verbal Expressions Examples Math Translation
Addition added to 6 added to y 6+y more than 8 more than x 8+x the sum of the sum of x and z x+z increased by t increased by 9 t+9 the total of the total of 5 and y 5+y
Subtraction minus x minus 2 x-2 less than 7 less than t t-7 subtracted from 5 subtracted from 8 8 – 5 decreased by m decreased by 3 m-3 the difference the difference between y and 4 y-4 between
Multiplication times 10 times 2 10 X 2 of one half of 6 (1/2) X 6 the product of the product of 4 and 3 4 X 3 multiplied by y multiplied by 11 11y
Division divided by x divided by 12 x/12 the quotient of the quotient of y and z y/z
the ratio of the ratio of t to 9 t/9
Power the square of the square of x x2 the cube of the cube of z z3 squared y squared y2
Equivalency equals 1+2 equals 3 1+2 = 3 is 2 is half of 4 2 = (½)X4 is the same as ½ is the same as 2/4 1 2 2 4 yields 3+1 yields 4 3+1 = 4 represents y represents x+1 y = x + 1
Comparison greater than -3 is greater than -5 -3 > -5 less than -5 is less then -3 -5 < -3 greater than or equal x is greater than or equal to 5 x ≥ 5 to at least x is at least 80 x ≥ 80 no less than x is no less than 70 x ≥ 70 less than or equal to x is less then or equal to -6 x ≤ -6 at most y is at most 23 y ≤ 23 no more than y is no more than 21 y ≤ 21 WORD PROBLEMS
Setting up word problems: 1) Find out what you are being asked to find. Set a variable to this unknown quantity. Make sure you know the units of this unknown (miles?, hours? ounces?) 2) If there is another unknown quantity, use the given information to put that unknown quantity in terms of the variable you have chosen. (For example, if total distance traveled is 700 miles, then part of the trip is x miles and the other part of the trip is 700 – x miles.) 3) Set up a table with a row for each unknown and columns made up of the terms of one of equations above (r*t = d, Pr = I, etc..) 4) Use the given information to combine the equations of each row of the table into one equation with one variable to solve for. 5) Check your equation by plugging in your value for x and seeing if your equation is true. 6) Once one variable is solved for, you can find the other unknown. (For example, is x = 100 miles, then the other part of the trip is 700 – 100 = 600 miles.) 7) Check your equation by plugging in your value for x and seeing if your equation is true.
Distance Problems Distance = rate * time If distance is in miles, and rate is in mph, then time must be in hours. If time is in minutes, then multiply time by 1 hr/60min to convert to hours.
PERCENT = part of a hundred
5 5% = .05 100
When converting from Percent to a Decimal, drop the % sign and move the decimal place to the LEFT TWO PLACES. 635% = 6.35 When converting from a Decimal to a Percent, move the decimal place to the RIGHT TWO PLACES and then attach a % sign to the end. .076 = 7.6% When converting a fraction to a percent, first convert the fraction to a decimal (see previous page).
Percent Problems: Amount = Percent * Base 4 is 40% of 10 Amt Example 1: t What is 30% of 60? Amt = Percent X Base Percent Base Amt = 30% X 60 Convert 30% to decimal. (in dec form) 30% = .30 Amt = .30 X 60 = 20 Example 2: Example 3: 200% of what is 400? 3 is what percent of 45? 200% is the Percent Converting Percent to a Decimal gives 200% = 2 Amt = 3 400 is the Amount Base = 45 “What” is the Base. Percent = Amt/ Base Base = Amt / Percent = 400 / 2 = 200 Percent = 3/45 = 0.06666….. Converting to Percent using % symbol gives 6.66666…% which rounds to 6.67% WORK Rate of Work * Time Worked = Part of Tasked Completed If someone can do a job in 60min, their rate of work is 1 joh/60min. If someone else can do the same job in 40minutes, their rate of work is 1 job/40min. The TIME to get the same job done TOGETHER can be found by Adding their parts together to make 1 whole job.
Similar Triangles
Triangles are similar if at least 2 corresponding angles are the same in each triangle.
Pythagorean Theorem The longest side of a right triangle is called the "hypotenuse", so the formal definition is:
In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, the square of a (a²) plus the square of b (b²) is equal to the square of c (c²):
a2 + b2 = c2 FRACTIONS Numerator A fraction is just a division problem. = Numerator ÷ Denominator Denominator
A fraction is in LOWEST TERMS when the numerator and denominator have no common factors. 6 3 is not in lowest terms, is in lowest terms 10 5
3 Mixed Number - A number, such as 6 , consisting of an integer and a fraction. A mixed number is just the sum of a 5 whole number and a fraction.
Improper Fraction - A fraction in which the numerator is larger than the denominator. Converting from mixed number to improper fraction: 3 65 3 33 6 5 5 5 Mixed numbers must be converted to improper fractions or decimals before doing ANY MULTIPLICATION OR DIVISION OPERATIONS on them. A fraction can be converted into a decimal by dividing: Numerator ÷ Denominator denominator numerator When ADDING or SUBTRACTING FRACTIONS, they must have the same denominator, then you just add the numerators and leave the denominator the same. 1 3 6 8 The denominators, 6 and 8, are not the same, so we must find the LEAST COMMON DENOMINATOR to convert these fractions into equivalent ones with the same denominator. The LCM of 6 and 8 is the SMALLEST NUMBER THAT BOTH 6 and 8 can go into. Choose the larger denominator (which is 8 in this case) and start taking multiples until 6 can go into it. Does 6 go into 8? NO Does 6 go into 8x2? NO Does 6 go into 8x3? Yes, 6 goes into 24. Therefore 24 is the LCM. Multiply the numerator and denominator of each fraction by whatever it takes to get the LCM as the new denominator. Then once you have the same denominators in each fraction, just add the numerators and leave the denominator the same. 1 4 3 3 4 9 13 6 4 8 3 24 24 24 MULTIPLYING FRACTIONS Multiplying Fractions uses a different rule. When multiplying fractions, you multiplying the numerators AND the denominators. 1 3 1 3 3 6 8 68 48
This fraction can simplified by canceling out common factors in the numerators and denominators (tops and bottoms)before multiplying across. 6 can be rewritten as 2x3, and the 3’s can be cancelled out. 1 3 1 3 1 3 1 6 8 68 2 38 16
DIVIDING FRACTIONS The rule for dividing fractions is simple. Just take the RECIPROCAL(flip the top and bottom) of the DIVISOR (the fraction to the right of the ÷ symbol) multiply 1 3 1 8 18 1 2 4 4 6 8 6 3 6 3 2 3 3 9 GEOMETRY x- intercept - point where graph crosses x-axis. y = 0 at this point. y-intercept – point where graph crosses y-axis. x = 0 at this point. y= - ½ x +1 slope = rise/run of a line, aka change in y/change in x. If linear equation is in the form The slope-intercept form of a linear equation is y = mx + b, where m is the slope and ( 0 ,b ) is the y-intercept. If two points of a line are known, (x1,y1) and (x2,y2), the slope can be found with this equation, the slope, y y m = 2 1 x2 x1 ORDERED PAIR: The first number in the ordered pair is the x-coordinate and the The point slope formula for a line with point second number in the ordered (x1, y1) and slope m is y – y1 = m(x – x1) pair is the y-coordinate.
Horizontal Lines = lines parallel to the x-axis with an equation in the form y = constant. Vertical Lines = lines parallel to the y-axis with an equation in the form x= constant.
Parallel lines – have the same slope. Perpendicular lines- form right angles. Their slopes are negative reciprocals of each other. Example: y=2x+1 and y= -½ x - 2 are perpendicular.
To graph a LINEAR INEQUALITY, First rewrite the inequality to solve for y. If the resulting inequality is y > …., Then make a dashed line and shade the area ABOVE the line. If the resulting inequality is y < ….., Then make a dashed line and shade the area BELOW the line. If the resulting inequality is y≥ ….., Then make a SOLID line and shade the area ABOVE the line. If the resulting inequality is y ≤ ……., Then make a SOLID line and shade the area BELOW the line.
If when isolating y, you must divide both sides of inequality by a negative number, Then the inequality sign must be SWITCHED. Example: -3y + 6x < 12 -3y < =6x + 12 divide through by -3 and switch inequality sign y > 2x - 4 Now graph a dashed line with y-intercept (0,4) and slope 2 and shade above the line.
Perimeter – distance around the edges of an object Perimeter of a square = 4s, where s = length of one side Perimeter of a rectangle = 2W + 2L, where W = width and L = length Perimeter of a triangle = side 1 + side 2 + side 3 Area – amount of surface covered by an object. Area of a square = s2 Area of a rectangle = L*W Area of a triangle = ½ bh, where b = length of base and h = height INTEGERS The set of natural numbers is {1,2,3,4,5,6,7,….}. These are basically the “counting numbers.” The set of whole numbers is the set of natural numbers and the number, 0. {0, 1, 2, 3, 4, 5, ….}
The set of integers is the set of whole numbers and their opposites. {…. -4,-3,-2,-1,0,1,2,3,4,….} The number 0 is an integer, but it is neither negative nor positive. For any two different places on the number line, the integer on the right is greater (>) than the integer on the left.
The absolute value (using the | | symbol) of a number is its distance from zero on the number line. The absolute value of a number is ALWAYS POSITIVE (or 0).
| 5| = 5, |-5| = 5, |3-8| = |-5| = 5, |3-3| = |0| = 0
|-4|=4 |4|=4 -4 is 4 units away +4 is 4units away from 0 from 0
Adding and Subtracting Integers
When adding two integers with the same sign, Subtracting a positive integer is the same as just ignore the signs, then attach them on the adding a negative integer. answer. -3 + -5 = - (3 + 5) = -8 5 – 3 = 5 + (-3) = 2 When adding two integers with different signs, take the absolute values (make both numbers -2 – 3 = -2 + (-3) = 1 positive), and subtract the smaller one from the larger one. The sign of the integer with the Multiplying and Dividing Integers larger absolute value will be the sign of your answer. (positive integer) X (positive integer) = (positive integer) 7 + (-8) (positive integer) ÷ (positive integer) = (positive integer) The absolute value of 7 is |7| = 7 (negative integer) X (negative integer ) = (negative integer) The absolute value of -8 is |-8| = 8 larger (negative integer) ÷ (negative integer ) = (negatrive integer) 8 – 7 = 1 (positive integer) X (negative integer) = (negatve integer) Remember in the original problem, the integer (positive integer) ÷ (negative integer) = (negative integer) whose absolute value was 8 was -8, so our (negative integer) X (positive integer ) = (negative integer) answer is negative. (negative integer) ÷ (positive integer ) = (negative integer) 7 + (-8) = -1 Subtracting a negative integer is the same as ______a ______integer. 3 – (-5) = 3 + 5 = 8 -2 – (-3) = -2 + 3 = 1 EXPONENTS & POLYNOMIALS POLYNOMIALS Exponent - A number or symbol, as 3 in (x + y)3, placed to the right of and above another number, variable, or expression polynomial – is a term or sum of terms in which all variables (called the base), denoting the power to which the base is to be have whole number exponents. Example: 3x, or x2 + 1, or -3x2 raised. Also called power. + 3x + 1 The exponent (or power) tells how many times the base is to be monomial – a number, a variable, or a product of numbers and multiplied by itself. variables. Example 1: Example: 3, 2x, -4x2 are all monomials. (x + y)3 = (x + y)(x+y)(x+y) binomial – the sum of two monomials that are unlike terms. Example 2: trinomial – the sum of three monomials that are unlike terms. (-3)4 = (-3)(-3)(-3)(-3) = 81 like terms – terms of a variable expression that have the same variable and the same exponent. Example: 3x and 3x2 are unlike terms, but 3x and 2x are like terms. Properties of Exponents factor – (in multiplication) a number being multiplied. If m and n are integers and x 0 Example: What are the factors of 121? 1, 11, and 121. If m and n are integers, then then 121 = 11 X 11, 121 = 1 X 121 m n mn m to factor a polynomial – to write a polynomial as a product of x x x x mn other polynomials n x to factor a trinomial of the form ax2 + bx + c - to express the If m and n are integers, then x trinomial as the product of two binomials. m n mn Example: x2 + 5x + 6 = (x+2)(x+3) (x ) x If n is a positive integer (-n is negative)to factor , and by grouping – to group and factor terms in a polynomial in such a way that a common binomial n 1 1 n If x is a real number and x 0 , and factor is found. x n n x then x x Example: 2x(x+1) – 3(x+1) = (x + 1)(2x – 3) factor completely – to write a polynomial as a product of factors x0 1 If n is an integer and b 0 , then that are nonfactorable over the integers. FOIL method – A method of finding the product of two n If m, n, and p are integers, then a a n binomials in which the sum of the products of the First n n n b bn terms, of the Outer terms, of the Inner terms, and of the Last (xy) x y , and terms is found. If n is a positive integer (-n is negative)Example: , and (x+2)(x+3) =x2+ 3x + 2x + 2*3 = x2 + 5x + 6 m n p mp np n n common factor – a factor that is common to two or more (x y ) x y a b numbers. Example: What are the common factors of 12 and b a 16x2? The factors of 12x are 1,2,3,4,6,12, and x The factors of 16x2are 1,2,4,8,16, x, x Rational Expoents The common factors of 12x and 16x2 are 1x, 2x, and 4x The Greatest Common Factor of 12x and 16x2 is 4x. a m / n = n a m Perfect-Square Trinomials
(a+b) 2 = a 2 + 2ab + b 2
(x+3)2 = x2 + 6x + 9
Difference of squares
a 2 - b 2 = (a+b)(a-b)
4x2 – 25 = (2x + 5)(2x – 5) Rules for Variable Expressions: parallel lines. They never intersect. A dependent system is the case Only like terms can be added, and when adding like terms, do not 20 4 when the equations represent the change the exponent of the variable. 2 2 2 same line. Therefore they intersect 5x + 3x = 8x 25 5 everywhere on the line. When multiplying variable expressions, add exponents of like variables (5xy3)(2y2)=10xy3+2 = 10xy5 25x 2 y 3 5x When taking powers of variable expression that is a monomial (one 4 term), multiply exponents of EVERY term inside the parentheses. 15xy 3y (2x3y4)3 = 23x3*3y4*3 = 8x9y12
When taking powers of a variable expression that is a binomial, trinomial or some other polynomial, use the rules of polynomial multiplication. 2 2 2 For example: (x+2) ≠ x + 2 A General Strategy for Factoring a Polynomial (x+2)2 = (x+2)(x+2) = x2+4x + 4 (FOIL METHOD) Example 2: (x2+3x+5)2 = (x2+3x+5)(x2+3x+5) 1. Do all the terms in the polynomial have a common factor? If =(x2+3x+5)x2 + (x2+3x+5)3x + (x2+3x+5)5 so, factor out the (DISTRIBUTIVE PROPERTY) Greatest Common Factor. Make sure that you don’t forget it in EXPRESSIONS EQUATIONS your final answer. 4 2 2 2 2 Example: 24x - 6x = 6x (4x - 1). Also look to see if the Examples: 3+2(1-4) , Examples: 3x + 2 = 5, other polynomial factor and be factored more. (4x2-1)=(2x- -3x+x, (3x+2)2 5x + 5y=10, x(x-5) = -6 1)(2x+1), so the final answer is Can be simplified Can be solved: 24x4 - 6x2 =6x2(2x-1)(2x+1), Ex1: Don’t forget order of Ex1: operations! 2. After factoring out the GCF (if there is one) count the number 3+2(1-4)2 can be simplified 3x 5 2 3 of terms in the remaining polynomial. to 3x 3 3+2(-3)2 which becomes 3+2(9) which becomes 3 3 Two terms: Is it a difference of squares? Factor by using: 2 2 3+18 which becomes 21. x 1 a -b = (a+b)(a-b) Ex2: Example: 36x2 – 49 = (6x)2 – 72 = (6x-7)(6x+7) -3x + x can be simplified to One solution If the polynomial can’t be factored, it is PRIME. -2x Ex2 :
5y 5x 10 Three terms: Is it a perfect square trinomial? 5y 5x 10 5 5 5 If it is it would be in the form a2x2 + 2abx + b2 , 2 y x 2 which is factored as (a+b) or a2x2 + 2abx + b2 which is factored as (a-b)2 Solution is all (x, y) Example: 4x2 + 12x + 9 = (2x)2 + 2(2)(3)x + 32 = that make this linear (2x + 3)2 equation true. 2 When graphed Is it of the form x + bx + c? this is a line. Ex3 : Factor by finding two numbers that multiply to c and add to b. x(x 5) 6 Example: x2 -3x - 4 = (x+1)(x-4) because 1*-4 = -4 and 1 + -4 = -3 x 2 5x 6 2 x 5x 6 0 Can’t find the numbers? Maybe the polynomial is (x 3)(x 2) 0 PRIME.
x 3, x 2 Is it of the form ax2 + bx + c? Two solutions Try factoring by the Grouping Method (or ac Can be evaluated: (3x+2)2 can be Can be evaluated to see if a 2 Method) or Trial and Error. evaluated at x= -1. (3(-1)+2) is (- solution is true. 2 2 2 Example: 2x + 13x + 15 (the a*c method means 3+2) which is (-1) which is 1. Is (3,4) a solution of y=-x+2? multiply 2*15 which is 30. 4 = -3+2=-1 NO Find factors of 30 that add up to the middle Can be reduced: Systems of Linear equations have term’s coefficient, which in this case is 13. either one solution (independent), 3*10=30 and 3+10 = 13. Split the middle term no solutions (inconsistent), or Examples: into two parts: infinitely many solutions 2x2 + 10x + 3x + 15 and then factor by grouping. (dependent). 2x(x+5)+3(x+5) = (2x+3)(x+5) An independent system is the case when the equations represent two intersecting lines. The solution is Those methods don’t work? Maybe the polynomial the intersection point. is PRIME. An inconsistent system is the case when the equations represent two Four terms: Try Factoring by Grouping. Group the 1st two Dividing Rational Expressions – change to a multiplication problem by terms and the last two terms. Factor out the Greatest changing the DIVISOR into it’s RECIPROCAL. Common Factor from each grouping. Then factor out the 3 x common binomial term. 1 LCD x(x 1) 2 2 1 1 x x 1 3 x 3. Always factor completely. Double check that each of your 2 x(x 1) x(x 1) x(x 1) factors can not be factored more. 5 5 2 5 x x 1 3(x 1) x2 x(x 1) 2 2 4. Check your work by multiplying the factors together. 3x 3 x x x Does it result in the original polynomial? 2x 3 x 3 2 SOLVING POLYNOMIAL EQUATIONS (2 SOLUTIONS): CHECK : 3 3 2 Adding and Subtracting Rational3 Expressions – Put Equation in standard form, ax + bx + c = 0. 2 1 2 2 2 3 1 x 31 3 1 1 2 2 2 3 methods: 4x 2 1 2x 2 x
1) SQUARE ROOT METHOD: If there is no bx term or if the Step 1: Factor the denominators, then find the LCM. The LCM of two equation is in the form (x+ k)2 + c = 0, then just get the constant c on polynomials is the simplest polynomial that contains the factors of each polynomial. To find the LCM of two or more polynomials, first factor one side, take ± the square of both sides and get x by itself. each polynomial completely. The LCM is the product of each factor the greater number of times it occurs in any one factorization. 2) FACTORING METHOD: If product ac has to factors that add up to c, then it is factorable. Factor it and use the Zero Product Product x 1 1st denominator : 2x 12x 1 to find the solutions. This says that if A*B=0, then A=0 or B=0. nd Example: x2 -2x = -3 2x 12x 1 x(2x 1) 2 denominator : x(2x 1) Standard form: x2 – 2x + 3 = 0. Factored: (x+1)(x-3) = 0 LCM x(2x 1)2x 1
So x+1 = 0, which gives x = -1, or another possible solution is x-3 = 0, Step 2: Change each rational expression so that the new denominator will which gives x = 3. be the LCM. You will multiply the numerator and denominator of each expression by whatever it takes to get the LCM as the new denominator. 3) USE QUADRATIC FORMULA: If the equation ax2+ bx+ c =0 x x 1 (2x 1) x2 2x 1 isnot factorable, then use quadratic formula. 2x 12x 1 x x(2x 1) (2x 1) x(2x 1)(2x 1) x(2x 1)(2x 1) Quadratic Formula
if ax 2 + bx + c = 0 Step 3: Add the two new fractions by adding the numerators and keeping (standard form of a quadratic equation) then the denominator (the LCM) the same. x2 2x 1 x = ( -b (b 2 - 4ac) ) / 2a x(2x 1)(2x 1)
Step 4: Now factor the resulting expression and cancel out any common RATIONAL EXPRESSIONS factors in the numerator and denominator.
x2 2x 1 (x 1)2 A rational expression is a fraction in which the numerator or denominator is a variable expression (such as a polynomial). A rational x(2x 1)(2x 1) x(2x 1)(2x 1) expression is undefined if the denominator has a value of 0. A rational expression is in SIMPLEST form when the numerator and Simplify Complex Fractions – Complex fractions are just rational denominator have no common factors other than 1. expressions with fractions within fractions. To simplify, find the LCM of 6x all the denominators of every fraction in the expression, then multiply the is not in simplest form. 9x2 main numerator and denominator by that LCM. Then simplify as usual. 2 is in simplest form. 3x 1 1 3 1 3 1 1 3 1(x ) (x ) 3 2 2 x x x x (x 1) x x x x 2 1 1 1 1 3 1 1 x (x3 ) (x3 ) x 1 x 1 Reducing to simplest form – factor the numerator and denominator, then x2 x3 x 2 x3 x2 x3 cancel out any common factors in the numerator and denominator (not common factors that are both in the numerator or both in the 3 denominator, e.g. side by side). LCD= x
Solving Equations with Fractions – multiply BOTH SIDES of the equation by the LCM of all denominators in the equation. Then solve as usual. Multiplying Rational Expressions – factor the numerators and denominators then cancel out common factors as above, then multiply the numerators and multiply the denominators. If the equation is one fraction set equal to another, this is called a PROPORTION.x 12 Solve by CROSS- MULTIPLYING,3 18 then isolating the variable. 18x 3(12) 36 18x 36 18 18 x 2 2 2 2 c a +b =c a Pythagorean Theorem: The sum of the squares of the legs b of a right triangle is equal to the square of the hypotenuse.