JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING POWER TRANSFORMER MODEL FOR COMPUTATION OF WINDING LOSSES AT HIGH FREQUENCIES D.S.TAKBHOURE 1, DR. N.D.GHAWGHAWE 2 1 MTech (EPS) student of Electrical Engineering at Govt. College of Engg Amravati 2Associate. Prof. Electrical Engg. Dept, G.C.O.E.Amravati, Maharashtra State, India.
[email protected], [email protected] ABSTRACT: During services the terminal of a transformer are subjected to a great variety of transient voltage wave shapes. Each of these transients affects the voltages at different locations inside the transformer. Some of them result in insulation failures. These failures are undesirable and costly events which affect the utility systems reliability. As such, they are of concern for utilities and transformer manufactures. For this reason, when building large power transformers, the design of the internal insulation structure is of considerable importance. Designing a cost effective and reliable insulation structure requires knowledge of the internal voltage distribution, the maximum voltage stresses and the times and duration of their occurrence. Engineers have extensively used detailed transformer models as an important tool in the design of the internal insulation structure of large power transformers. The behavior of large power transformer under transient conditions is of interest to both transformer designers and power engineers. The power engineer not only needs the models of transformer but also needs system in order to investigate the effects of power system transients. Key Words: Skin Effect. Proximity Effect, Inductance Calculation, Insulation Model, Transients
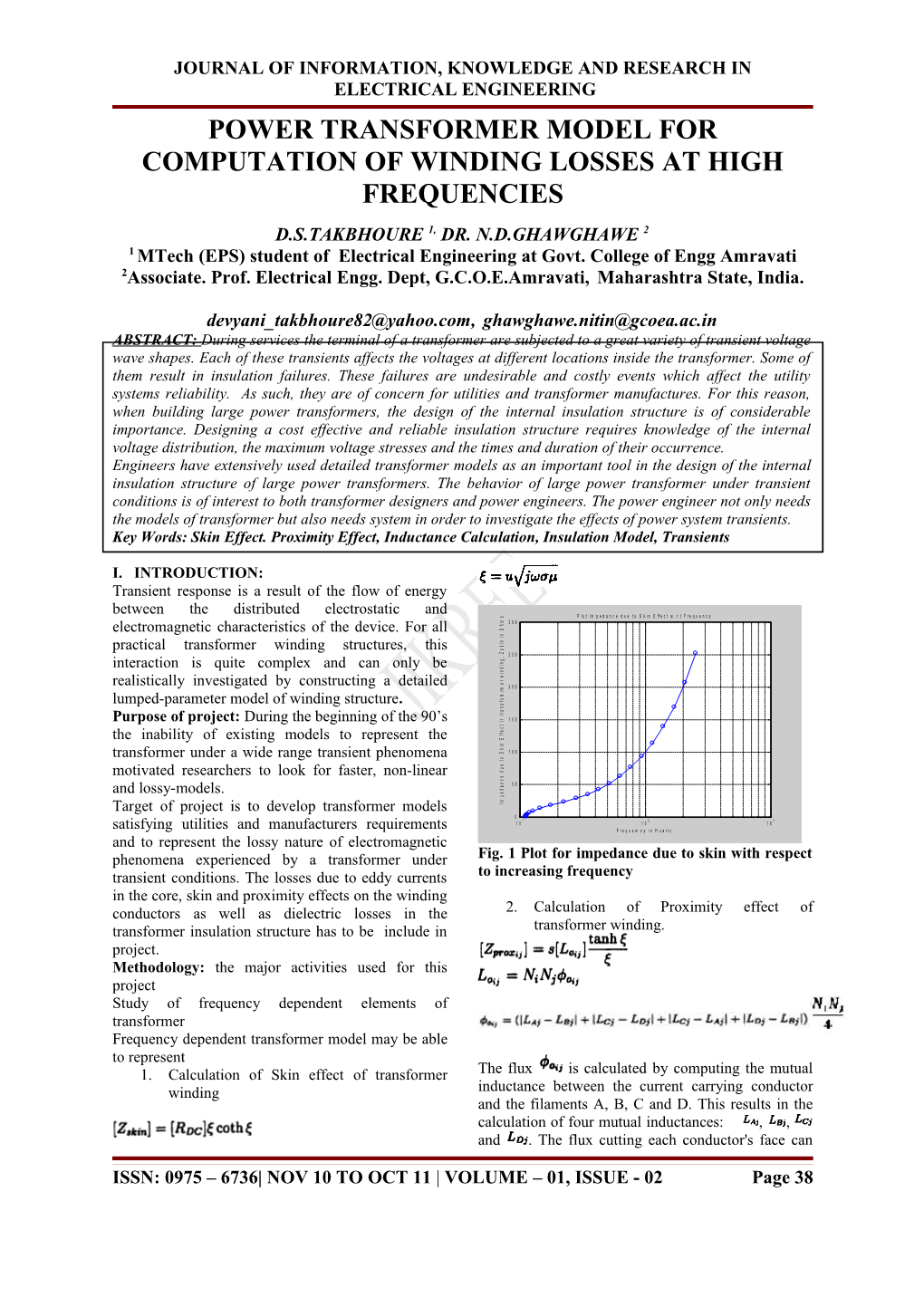
I. INTRODUCTION: Transient response is a result of the flow of energy between the distributed electrostatic and s P l o t I m p e d a n c e d u e t o S k i n E f f e c t w . r . t F r e q u e n c y
m 3 0 0 h O electromagnetic characteristics of the device. For all n i
n i k practical transformer winding structures, this s Z
, 2 5 0 g n i interaction is quite complex and can only be d n i w
r realistically investigated by constructing a detailed e
m 2 0 0 r m o f lumped-parameter model of winding structure. s n a r t
n
i 1 5 0 Purpose of project: During the beginning of the 90’s t c e f f E the inability of existing models to represent the n i k
S 1 0 0
transformer under a wide range transient phenomena o t
e u d
motivated researchers to look for faster, non-linear e c
n 5 0 a d and lossy-models. e p m Target of project is to develop transformer models I 0 1 2 3 1 0 1 0 1 0 satisfying utilities and manufacturers requirements F r e q u e m c y i n H e a r t z and to represent the lossy nature of electromagnetic phenomena experienced by a transformer under Fig. 1 Plot for impedance due to skin with respect transient conditions. The losses due to eddy currents to increasing frequency in the core, skin and proximity effects on the winding conductors as well as dielectric losses in the 2. Calculation of Proximity effect of transformer insulation structure has to be include in transformer winding. project. Methodology: the major activities used for this project Study of frequency dependent elements of transformer Frequency dependent transformer model may be able to represent 1. Calculation of Skin effect of transformer The flux is calculated by computing the mutual winding inductance between the current carrying conductor and the filaments A, B, C and D. This results in the calculation of four mutual inductances: , , and . The flux cutting each conductor's face can
ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 38 JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING be calculated by taking the difference between the 5. The effect of frequency on the mutual mutual inductances as follows: for the inner face coupling between winding section , the outer face , the top face , and the bottom face . These Modeling frequency dependent differences will represent the flux lines entering or elements in time domain leaving each of the four faces. It was difficult to determine, by using the sign of the inductance Developing 1. Lossy insulation model, differences, when the flux limes were entering or 2. leaving a face. Therefore, in order to calculate the total flux cutting the open conductor the absolute Lossy winding model, 3. Lossy core value of each difference was taken. Then, based on model, 4. Inductance model the fact that the sum of the total number of flux lines leaving and entering a volume adds to zero, was Assembling complete model expressed as follows. The lossy transformer model then verified using available experimental data for different transformers.
MATLAB programming is used to represent set of equations of lossy transformer.
Inductance Model Fig 2: Equivalent representation of two conductors. The inductance of a group of turns can be divided in three components: and air core inductance, iron core 3. calculation of Eddy current losses in core. leakage inductance and iron core magnetization inductance. The air core inductance represents the total inductance when the core is absent. The iron Where core leakage inductances represent the flux linkages = Core length, m having a path wholly or partially in air. They takes = Thickness of lamination into account the change produced by the presence of =Conductivity of lamination material. the core on the flux in the air. The iron core = Permeability of free space magnetizing inductance represents the flux linking all the turns of the winding having a path totally inside = Number of turns of the coil the core. =Total cross sectional area of laminations. =Frequency in rad/sec
1 1 x 1 0 P l o t C o r e I m p e d a n c e w . r . t F r e q u e n c y 8
7 e
r 6 o c Z
, g n i d n
i 5 w
r e m r m
o 4 f s n a r t
f o
e 3 c n a d e p m I
2 e r o C
1 Fig.4; Winding lumped parameter model
0 5 6 7 8 9 1 0 1 1 1 2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 F r e q u e m c y i n H e a r t z Fig .3 plot for core impedance of transformer winding with respect to increasing frequency
4. Calculation of Insulation losses
ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 39 JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING Fig 6: Plot for inductance due to proximity effect w.r.t frequency
4 x 1 0 P l o t f o r I m p e d a n c e d u e t o p r o x i m i t y e f f e c t w . r . t F r e q u e n c y 1 4
1 2 x
= Total number of turns in section i and j o r p Z
, g
n 1 0 = Relative reluctivity i d n i w
r
= Core length, m e m r 8 m o = Outer radius of coil section i and j, m f s n a r t
f o
= Outer radius of coil section i and j, m
e 6 c n a d
= Height of coil section i and j, m e p m i
y 4 t = Permeability of free space. i m i x o r p = Core radius. 2
0 -1 0 1 2 3 4 5 6 = Modified Bessel function of first 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 kind. F r e q u e m c y i n H e a r t z
= Modified Bessel function of Fig 7: Plot for impedance due to proximity effect second kind. w.r.t frequency
-9 = Lanczos sigma factor. x 1 0 P l o t f o r I N D U C T A N C E d u e t o p r o x i m i t y e f f e c t w . r . t D I S T A N C E B E T W E E N C E N T E R S O F C O I L S E C T I O N 4 . 5
4 x o r p L
, g n i d
n 3 . 5 i w
r e m r m o f s n
a 3 r t
f o
e c n a t c u d
n 2 . 5 i
y t i m i x o r p
2
1 . 5 0 . 0 2 0 . 0 4 0 . 0 6 0 . 0 8 0 . 1 0 . 1 2 0 . 1 4 0 . 1 6 0 . 1 8 0 . 2 0 . 2 2 D I S T A N C E B E T W E E N C E N T E R S I N m m
Fig 8: Plot for Inductance due to proximity effect w.r.t. Distance between centers of coil section
Winding losses: The most challenging phenomena to model in a transformer is the magnetic flux interaction involving the different winding sections and the core. Fig 5:Winding geometry Historically, this phenomenon has been modeled by dividing the flux in two main components: the
- 9 x 1 0 P l o t f o r I N D U C T A N C E d u e t o p r o x i m i t y e f f e c t w . r . t F r e q u e n c y 4 . 5 common and leakage flux. Developing a transformer model capable of representing the magnetic flux
x 4 behavior inside a real transformer for a wide range of o r p L
,
g different circumstances is a challenging task. In this n i d n i w
3 . 5 r paper the damping effect of the losses associated to e m r m
o leakage flux components is studied. f s n a r t
3 f o
E C N A T C
U 2 . 5 D N I
y t i m i x o r
p 2
1 . 5 0 1 0 F r e q u e m c y i n H e a r t z
ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 40 JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING
- 8 x 1 0 1 . 7 9 5 F r e q u e n c y d e p e n d e n t D i s k t o D i s k C a p a c i t a n c e 1 . 7 9
1 . 7 8 5 e c n a
t 1 . 7 8 i c a p
a 1 . 7 7 5 c
k s i
D 1 . 7 7
o t
k
s 1 . 7 6 5 i D
1 . 7 6
1 . 7 5 5
2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 F r e q u e n c y Fig 11: Plot for disk to disk capacitance w.r.t. frequency
-8 x 1 0 1 . 1 9 5 F r e q u e n c y d e p e n d e n t S e r i e s C a p a c i t a n c e
1 . 1 9
1 . 1 8 5 e c n a t i c a
p 1 . 1 8 a c
s e i r e S
1 . 1 7 5
1 . 1 7
1 . 1 6 5 2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 Fig.9 Algorithm to calculate inductance due to F r e q u e n c y proximity effect. Fig 12: Plot for Series capacitance w.r.t. frequency
- 1 3 x 1 0 Capacitance Model 4 . 8 8 The inter turn capacitance and capacitance F r e q u e n c y d e p e n d e n t G r o u n d C a p a c i t a n c e 4 . 8 6 between sections are calculated based on the type of winding used in the transformer being studied. In the 4 . 8 4 e c n a t i existing program this can be done for the following c 4 . 8 2 a p a c
d winding types: layers, discs, helical. The capacitance n
u 4 . 8 o r is an equivalent energy storing capacitance for the G section of interest and as such is completely general. 4 . 7 8
4 . 7 6
4 . 7 4 2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 -9 x 1 0 F r e q u e n c y 1 . 5 2 5 F r e q u e n c y d e p e n d e n t T u r n t o T u r n C a p a c i t a n c e Fig 13: Plot for ground capacitance w.r.t. 1 . 5 2 frequency 1 . 5 1 5
- 8
e 1 . 5 1 x 1 0 c
n 5 a t i
c F r e q u e n c y d e p e n d e n t I n n e r W i n d i n g t o C o r e C a p a c i t a n c e a 1 . 5 0 5 p a c
e 4 . 9 8 n c r u n T 1 . 5 a
t i o t c
a n r
p 4 . 9 6 u a
T 1 . 4 9 5 c
g n i d
1 . 4 9 n
i 4 . 9 4 W
o t 1 . 4 8 5 g n
i 4 . 9 2 d n 1 . 4 8 i 2 3 4 5 6 W 1 0 1 0 1 0 1 0 1 0 4 . 9 F r e q u e n c y
Fig 10: Plot for Turn to turn capacitance w.r.t. 4 . 8 8 2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 frequency F r e q u e n c y
ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 41 JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING Fig 14: Plot for Winding to winding capacitance bilinear transformation and the properties of the z- w.r.t. frequency transformer were applied to obtain the network nodal system of equations in the time domain. The 3 5 s
e representation of the damping effect of losses in the c n a t i 3 0 internal transient voltage response of large power c a p a
c transform was achieved by replacing the component
t 2 5 n u
h of the winding losses lumped parameters model with s
d n
a 2 0 frequency-dependent element.
s e i r
e REFERENCES s
o 1 5 t
e [1] M. Gutierrez, R.C. Degeneff, P.J. McKenny a d u d
s J.M. Schneider, "Linear, lumped parameter e 1 0 s s o
L transformer model reduction technique," IEEE paper
c i r
t 5
c no. 93 SM 394-7 PWRD. e l e i
D [2] R.C. Degeneff, M. Gutierrez and M. Vakilian, 0 2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 "Lumped parameter transformer model reduction F r e q u e n c y technique," IEEE paper no. 94 SM 409-9 PWRD. Fig 15: Plot for dielectric losses due to series and [3] F. de Leon and A. Semlyen, "Complete shunt capacitance w.r.t. frequency transformer model for electromagnetic trmients," IEEE Transactions on Power Delivery, vol. 9, no. 1, pp. 231-239, January 1994. [4] V.I. Kogan, J.A. Fleeman, J.H. Provanzana, D.A. Yanucci and W.N. Kennedy, "Failure analysis of EHV transformers," IEEE transactions on Power Delivery, pp. 672-683, April 1988. [5] P.I. Fergestad and T. Henriksen, “Transient oscillations in multi winding transformers," lEEE Transactions on PAS, vol. PAS93, pp. 500-507, 1974. [6] W.N. White, "An examination of core steel eddy current reaction effect on transformer transient oscillatory phenomena," General Electric Technical Information Series, TIS 77PTD012, April 1977. [7] W.N. White, “Inductance models of power Fig 16: Complete Transformer model transformers," General Electric Technical Information Series, TIS 78PTD003, April 1978. Discussion [8] R.C. Degeneff, "A general method for Frequency dependent Lossy-transformer model to determining resonances in transformer windings," calculate the internal transformer voltage response of IEEE transactions on PAS, vol. 96, no. 2, pp. 423- large power transformer has been presented in this 430, March/April 1977. paper. This model was developed using a starting [9] R.C. Degeneff, W. Neugebaur, J. Panek, M.E. point, a lossless lumped parameter transformer model McCallum and C.C. Honey, "Transformer response based on the calculation of the unconnected to system switching voltages," IEEE transactions on inductance matrix. The damping effect of losses due Power Apparatus and Systems, vol. Pas-101, no. 6, to the skin and proximity effect on the winding’s pp. 1457-1465, June 1982. conductors, the eddy current in the core and the [10] D. J. Wilcox, M. Conlon and W.G. Hurley, dielectric losses in the transformer’s insulations "Calculation of self and mutual impedances for coils structure were represented in this model. on ferromagnetic cores," IEE Proceedings, vol. 135, To construct the model, it was necessary to obtain the Pt . A, no. 7, pp. 470-476, September 1988. characteristics of each damping mechanism as [11] D.J. Wilcox, W.G. Hurley and M. Conion, function of frequency. For this purpose analytical "Calculation of self and mutual impedances between formulas were used to represent the electromagnetic sections of transformer windings," IEE Proceedings, phenomena involving eddy currents. The frequency vol. 136, Pt. C, no. 5, pp. 308-314, September 1989. characteristics of the insulation losses were modeled [12] F. de Leon and A. Semlyen, "Detailed modeling by combining an equivalent parallel plate capacitor of eddy current effects for transformer transients," representation and empirical data in the form of the IEEE transactions on Power Delivery, vol. 9, no. 2, dielectric material properties. pp. 1143-1160, April 1994. The frequency characteristics were approximated [13] T. Henricksen, “Including high order rational using rational polynomial forms in the s-plane. The functions in EMTP: A comparison between ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 42 JOURNAL OF INFORMATION, KNOWLEDGE AND RESEARCH IN ELECTRICAL ENGINEERING alternative methods with emphasis on accuracy," IEEE Transactions on Power Delivery, vol. 12, no. 1, pp. 1143-1150, January 1997. [14] R. Bartnikas, "Dielectric loss in insulating liquids," IEEE Transactions on Electrical Insulation, vol. EI-2, no. 1, pp. 33-54, 1967. [15] R. Bartnikas, "Dielectric losses in solid-liquid insulating systems," IEEE Transactions on Electrical Insulation, vol. EI-5, no. 4, pp. 113-121, 1970. [16] M.J. Jeroense and F.H. Kreuger, "Electrical conduction in HVDC mass-impregnated paper cable," IEEE Transactions on Dielectric and Electrical insulation, vol. 2, no. 5, pp. 718-723, October 1995. [17] F. De Leon and A. Semlyen, "Efficient calculation of elementary parameters of transformers," IEEE Transaction on Power Delivery, vol. 7, no. 1, pp. 376-382, January 1992. [18] S.V. Kulkarni and S.A. Khaperde “Transformer Engineering, Design and Practice,” Marcel Dekker, Inc, New York, Bsel 1972. [19] Richard L. Bean, et al “Transformer for the Electric Power Industry” McGraw Hill Book Company, Inc, New York Toronto London 1959
ISSN: 0975 – 6736| NOV 10 TO OCT 11 | VOLUME – 01, ISSUE - 02 Page 43