DOCSLIB.ORG

Confidential Channels, Encryption, and Ciphers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Confidential Channels, Encryption, and Ciphers Confidential Channels, Encryption, and Ciphers • Readings – Sections 2.1 – 2.4, 3.1 – 3.2 1 Cryptography • Greek for “hidden writing” • “The art and science of keeping messages secure” • A field of study relating to the above • Note: Cryptology is often defined to include the fields of: –Cryptography –Cryptanalysis –Steganography 2 What is encryption? • Encryption is used to achieve confidentiality • Alice and Bob, wish to communicate secretly. • Curious Carl wants to listen into their private 01001110… chat. As root, try: tcpdump -a -s 0 3 Ciphers • Plaintext • Ciphertext • Encipher: transform plaintext into ciphertext (encrypt) • Decipher: transform ciphertext into plaintext (decrypt) • Key: used in the transformation between plaintext and ciphertext. • Cipher: an encryption (and decryption) algorithm – Symmetric or secret key – Asymmetric or public/private key • Goal of good ciphers: make the ciphertext look like “random bits” 4 Ciphers • Ciphers operate to “garble” their input to make it unintelligible. The output of a cipher (ciphertext) does not bear any clear relation to the input (clear- text or plaintext). – The earliest recorded example of the use of a cipher is by Julius Caesar to his generals: He would shift each letter to the third letter following it in the alphabet. • Example: Attack now Dwwdfn qrz • How can you cryptanalyze this cipher? 5 Generalizing the Caesar Cipher (a substitution cipher) • Caesar: given plaintext p, use s, where s = E(p + 3) mod 26 • Can obviously use s = E(p + k) mod 26 for arbitrary k. How many keys are there? • Mono-alphabetic cipher: use an arbitrary permutation of the 26 letters. – N! permutations or keys – Many more keys – how much harder to analyze? 6 Assumptions about cipher design • The adversary knows the cipher algorithm. – also the design process, the implementation, etc. • To achieve secrecy, ciphers use keys. • A key is an auxiliary input to the algorithm that must be kept private. – Only the key value is private. It is assumed that the enemy knows how keys are generated. 7 Example: Vigenere cipher Key VECTOR (21,4,2,19,14,17) W E W I L L M E E T A T M I D N I G H T 22 4 22 8 11 11 12 4 4 19 0 19 12 8 3 13 8 6 7 19 21 4 2 19 14 17 21 4 2 19 14 17 21 4 2 19 14 17 21 4 17 8 24 1 25 2 7 8 6 12 14 10 7 12 5 6 22 23 2 23 R I Y B Z C H I G M O K H M F G W X C X Courtesy of Giuseppe Ateniese Vigenere Cipher • Normally the key of Vigenere cipher is given as a “keyword” instead of a vector of integer values, for example an English word or even a sentence – For example, if a keyword is “leg”, then the corresponding values of “leg” are repeated applied to plaintext to obtain ciphertext – Easy to remember 9 Breaking the Vigenere Cipher • The probability distribution of characters 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 A C E G I K M O Q S U W Y Courtesy of Giuseppe Ateniese Strategy for breaking this cipher • We start with the above distribution of letters in the alphabet. Notice how the letter E is so more frequent than other characters that it can always be identified given enough ciphertext, if the cipher preserves character probabilities. • Moreover, it is not shown here, but E tends to appear in patterns, such as following H or preceding R. H, a common letter, tends to follow T. The letter I, also very frequent, tends to be followed by N, and so on. (digrams) • Suppose that the adversary guesses the key length to be equal to 4 in our Vigenere example. Will get each fourth character and create four collections: 11 Looking at the example again K VECTOR (21,4,2,19,14,17) W E W I L L M E E T A T M I D N I G H T 22 4 22 8 11 11 12 4 4 19 0 19 12 8 3 13 8 6 7 19 21 4 2 19 14 17 21 4 2 19 14 17 21 4 2 19 14 17 21 4 17 8 24 1 25 2 7 8 6 12 14 10 7 12 5 6 22 23 2 23 R I Y B Z C H I G M O K H M F G W X C X 12 Computing Distributions for various • By computing the distribution of each fourth letter, and comparing with the distribution of English, the adversary can check if there is a match. • With enough ciphertext, the adversary will be able to find the key length when the distributions match. Here the adversary would find that the correct key length is six. • The adversary would collect every sixth letter and, given enough ciphertext, be able to determine which letter corresponds to „E‟ in each distribution. That determines the key character for the distribution, decrypting that collection. 13 Index of coincidence 14 Another Class of Ciphers: Transposition ciphers • Plaintext – attackatdawn • Cipher 3 1 4 2 - the key – Put plaintext in a n by m matrix (example 3 by 4) a t t a – Re-arrange the column according to the key. For c k a t example, put column 1 in original matrix to column 3 – Output letters vertically from d a w n top using key number order • Ciphertext – TKAATNACDTAW 15 Choosing a Cipher • Ciphers are vulnerable to many known analysis techniques, and one must count on new attacks being discovered • General advice: – Avoid proprietary commercial ciphers whose design has not been publicly scrutinized. – Do not develop your own if good alternatives exist: Adopt standards. • Why? Standardization process ensures that many experts have explored the cipher for weaknesses • Fundamental Tenet of Cryptography – If lots of smart people have failed to solve a problem, then it probably won’t be solved (soon) 16 General Encryption Schemes 17 Symmetric vs. Asymmetric • If the encryption and decryption keys are equal, the scheme is said to be symmetric • If the encryption and decryption keys differ, and moreover the decryption key cannot be computed from knowledge of the algorithm and encryption key, the scheme is asymmetric • Note: “cannot be computed” really means “computationally infeasible” 18 Security of ciphers From the Vigenere cipher to the Vernam one- time pad 19 Attacks on Encryption Schemes • PASSIVE – Ciphertext only • Only the ciphertext is available. Use statistical methods and correlations – Known-plaintext • One or more pairs of (plaintext, ciphertext) available • Analyst could likely have this • ACTIVE – Chosen plaintext (CPA) • Adversary can obtain encrypted versions of (chosen) plaintext – Adaptive CPA • Can obtain encrypted versions based on analysis of previous versions – Chosen ciphertext (CCA1) • Given ciphertext, can get plaintext – Adaptive CCA (CCA2) 20 Outcomes of Attacks (Goals) • Total Break (key recovery) - most ambitious – This is the worst outcome possible • Recovery of plaintext - less ambitious – less bad an outcome • Distinguishability between two possible decryptions of a given ciphertext - even less ambitious – may even be willing to settle for this Note: IND (indistinguishability) is used to denote “not distinguishability” • Most stringent security: IND-CCA2 21 Perfect Cipher • If the Vigenere cipher has key at least as long as the plaintext, is chosen at random, and used only once: – The scheme is called the Vernam One-Time Pad – It is provably unbreakable, even if the adversary has infinite computational power • Reasoning: Given some ciphertext, any message of the same size would encrypt to the observed ciphertext under some key. 22 One Time Pad • Plaintext is xor'ed with a string of random bits • The result is a random bit string • Problems – Key must be same size as plaintext – Generating random bits 23 Example of a One-Time Key • Plaintext: T E D • ASCII of plaintext: 0101 0100 0100 0101 0100 0100 • Key (random): 0110 0110 0111 0011 0001 0010 • Ciphertext: 0011 0010 0011 0110 0101 0110 • ASCII of Ciphertext: 2 6 V 24 Perfect Secrecy • Shannon proved that the only cipher that is secure against an all-powerful adversary – Has key length equal to, or larger than the message – The key is random – Used only once – As inefficient as the Vernam one-time pad 25 Modern Ciphers • Operate on binary plaintext • Use binary keys of fixed length • Different types of ciphers: – Public key/asymmetric ciphers – Symmetric ciphers • Stream ciphers (RC4, A5/x, Helix, SEAL) • Block ciphers (Triple-DES, Blowfish, AES) 26 Modern Cipher Operations • Two basic operations – Substitution: substitute a code symbol (for instance bit octets) for another. • Example: shifts (Vigenere cipher), xor • 10110111 11001010 – Permutation: transpose or reorder the symbols (bits) present in the code • 10110111 11111100 • Both steps are needed for security 27 Reading Assignments • Sections 3.3, 4.1, 4.2 • Paper 2 28.
Load more

Recommended publications
  • Classical Encryption Techniques
    CPE 542: CRYPTOGRAPHY & NETWORK SECURITY Chapter 2: Classical Encryption Techniques Dr. Lo’ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan Dr. Lo’ai Tawalbeh Fall 2005 Introduction Basic Terminology • plaintext - the original message • ciphertext - the coded message • key - information used in encryption/decryption, and known only to sender/receiver • encipher (encrypt) - converting plaintext to ciphertext using key • decipher (decrypt) - recovering ciphertext from plaintext using key • cryptography - study of encryption principles/methods/designs • cryptanalysis (code breaking) - the study of principles/ methods of deciphering ciphertext Dr. Lo’ai Tawalbeh Fall 2005 1 Cryptographic Systems Cryptographic Systems are categorized according to: 1. The operation used in transferring plaintext to ciphertext: • Substitution: each element in the plaintext is mapped into another element • Transposition: the elements in the plaintext are re-arranged. 2. The number of keys used: • Symmetric (private- key) : both the sender and receiver use the same key • Asymmetric (public-key) : sender and receiver use different key 3. The way the plaintext is processed : • Block cipher : inputs are processed one block at a time, producing a corresponding output block. • Stream cipher: inputs are processed continuously, producing one element at a time (bit, Dr. Lo’ai Tawalbeh Fall 2005 Cryptographic Systems Symmetric Encryption Model Dr. Lo’ai Tawalbeh Fall 2005 2 Cryptographic Systems Requirements • two requirements for secure use of symmetric encryption: 1. a strong encryption algorithm 2. a secret key known only to sender / receiver •Y = Ek(X), where X: the plaintext, Y: the ciphertext •X = Dk(Y) • assume encryption algorithm is known •implies a secure channel to distribute key Dr.
    [Show full text]
  • Recommendation for Block Cipher Modes of Operation Methods
    NIST Special Publication 800-38A Recommendation for Block 2001 Edition Cipher Modes of Operation Methods and Techniques Morris Dworkin C O M P U T E R S E C U R I T Y ii C O M P U T E R S E C U R I T Y Computer Security Division Information Technology Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899-8930 December 2001 U.S. Department of Commerce Donald L. Evans, Secretary Technology Administration Phillip J. Bond, Under Secretary of Commerce for Technology National Institute of Standards and Technology Arden L. Bement, Jr., Director iii Reports on Information Security Technology The Information Technology Laboratory (ITL) at the National Institute of Standards and Technology (NIST) promotes the U.S. economy and public welfare by providing technical leadership for the Nation’s measurement and standards infrastructure. ITL develops tests, test methods, reference data, proof of concept implementations, and technical analyses to advance the development and productive use of information technology. ITL’s responsibilities include the development of technical, physical, administrative, and management standards and guidelines for the cost-effective security and privacy of sensitive unclassified information in Federal computer systems. This Special Publication 800-series reports on ITL’s research, guidance, and outreach efforts in computer security, and its collaborative activities with industry, government, and academic organizations. Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose.
    [Show full text]
  • Polish Mathematicians Finding Patterns in Enigma Messages
    Fall 2006 Chris Christensen MAT/CSC 483 Machine Ciphers Polyalphabetic ciphers are good ways to destroy the usefulness of frequency analysis. Implementation can be a problem, however. The key to a polyalphabetic cipher specifies the order of the ciphers that will be used during encryption. Ideally there would be as many ciphers as there are letters in the plaintext message and the ordering of the ciphers would be random – an one-time pad. More commonly, some rotation among a small number of ciphers is prescribed. But, rotating among a small number of ciphers leads to a period, which a cryptanalyst can exploit. Rotating among a “large” number of ciphers might work, but that is hard to do by hand – there is a high probability of encryption errors. Maybe, a machine. During World War II, all the Allied and Axis countries used machine ciphers. The United States had SIGABA, Britain had TypeX, Japan had “Purple,” and Germany (and Italy) had Enigma. SIGABA http://en.wikipedia.org/wiki/SIGABA 1 A TypeX machine at Bletchley Park. 2 From the 1920s until the 1970s, cryptology was dominated by machine ciphers. What the machine ciphers typically did was provide a mechanical way to rotate among a large number of ciphers. The rotation was not random, but the large number of ciphers that were available could prevent depth from occurring within messages and (if the machines were used properly) among messages. We will examine Enigma, which was broken by Polish mathematicians in the 1930s and by the British during World War II. The Japanese Purple machine, which was used to transmit diplomatic messages, was broken by William Friedman’s cryptanalysts.
    [Show full text]
  • Index-Of-Coincidence.Pdf
    The Index of Coincidence William F. Friedman in the 1930s developed the index of coincidence. For a given text X, where X is the sequence of letters x1x2…xn, the index of coincidence IC(X) is defined to be the probability that two randomly selected letters in the ciphertext represent, the same plaintext symbol. For a given ciphertext of length n, let n0, n1, …, n25 be the respective letter counts of A, B, C, . , Z in the ciphertext. Then, the index of coincidence can be computed as 25 ni (ni −1) IC = ∑ i=0 n(n −1) We can also calculate this index for any language source. For some source of letters, let p be the probability of occurrence of the letter a, p be the probability of occurrence of a € b the letter b, and so on. Then the index of coincidence for this source is 25 2 Isource = pa pa + pb pb +…+ pz pz = ∑ pi i=0 We can interpret the index of coincidence as the probability of randomly selecting two identical letters from the source. To see why the index of coincidence gives us useful information, first€ note that the empirical probability of randomly selecting two identical letters from a large English plaintext is approximately 0.065. This implies that an (English) ciphertext having an index of coincidence I of approximately 0.065 is probably associated with a mono-alphabetic substitution cipher, since this statistic will not change if the letters are simply relabeled (which is the effect of encrypting with a simple substitution). The longer and more random a Vigenere cipher keyword is, the more evenly the letters are distributed throughout the ciphertext.
    [Show full text]
  • Automating the Development of Chosen Ciphertext Attacks
    Automating the Development of Chosen Ciphertext Attacks Gabrielle Beck∗ Maximilian Zinkus∗ Matthew Green Johns Hopkins University Johns Hopkins University Johns Hopkins University [email protected] [email protected] [email protected] Abstract In this work we consider a specific class of vulner- ability: the continued use of unauthenticated symmet- In this work we investigate the problem of automating the ric encryption in many cryptographic systems. While development of adaptive chosen ciphertext attacks on sys- the research community has long noted the threat of tems that contain vulnerable format oracles. Unlike pre- adaptive-chosen ciphertext attacks on malleable en- vious attempts, which simply automate the execution of cryption schemes [17, 18, 56], these concerns gained known attacks, we consider a more challenging problem: practical salience with the discovery of padding ora- to programmatically derive a novel attack strategy, given cle attacks on a number of standard encryption pro- only a machine-readable description of the plaintext veri- tocols [6,7, 13, 22, 30, 40, 51, 52, 73]. Despite repeated fication function and the malleability characteristics of warnings to industry, variants of these attacks continue to the encryption scheme. We present a new set of algo- plague modern systems, including TLS 1.2’s CBC-mode rithms that use SAT and SMT solvers to reason deeply ciphersuite [5,7, 48] and hardware key management to- over the design of the system, producing an automated kens [10, 13]. A generalized variant, the format oracle attack strategy that can entirely decrypt protected mes- attack can be constructed when a decryption oracle leaks sages.
    [Show full text]
  • Secure Communications One Time Pad Cipher
    Cipher Machines & Cryptology © 2010 – D. Rijmenants http://users.telenet.be/d.rijmenants THE COMPLETE GUIDE TO SECURE COMMUNICATIONS WITH THE ONE TIME PAD CIPHER DIRK RIJMENANTS Abstract : This paper provides standard instructions on how to protect short text messages with one-time pad encryption. The encryption is performed with nothing more than a pencil and paper, but provides absolute message security. If properly applied, it is mathematically impossible for any eavesdropper to decrypt or break the message without the proper key. Keywords : cryptography, one-time pad, encryption, message security, conversion table, steganography, codebook, message verification code, covert communications, Jargon code, Morse cut numbers. version 012-2011 1 Contents Section Page I. Introduction 2 II. The One-time Pad 3 III. Message Preparation 4 IV. Encryption 5 V. Decryption 6 VI. The Optional Codebook 7 VII. Security Rules and Advice 8 VIII. Appendices 17 I. Introduction One-time pad encryption is a basic yet solid method to protect short text messages. This paper explains how to use one-time pads, how to set up secure one-time pad communications and how to deal with its various security issues. It is easy to learn to work with one-time pads, the system is transparent, and you do not need special equipment or any knowledge about cryptographic techniques or math. If properly used, the system provides truly unbreakable encryption and it will be impossible for any eavesdropper to decrypt or break one-time pad encrypted message by any type of cryptanalytic attack without the proper key, even with infinite computational power (see section VII.b) However, to ensure the security of the message, it is of paramount importance to carefully read and strictly follow the security rules and advice (see section VII).
    [Show full text]
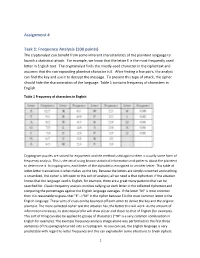
  • Assignment 4 Task 1: Frequency Analysis (100 Points)
    Assignment 4 Task 1: Frequency Analysis (100 points) The cryptanalyst can benefit from some inherent characteristics of the plaintext language to launch a statistical attack. For example, we know that the letter E is the most frequently used letter in English text. The cryptanalyst finds the mostly-used character in the ciphertext and assumes that the corresponding plaintext character is E. After finding a few pairs, the analyst can find the key and use it to decrypt the message. To prevent this type of attack, the cipher should hide the characteristics of the language. Table 1 contains frequency of characters in English. Table 1 Frequency of characters in English Cryptogram puzzles are solved for enjoyment and the method used against them is usually some form of frequency analysis. This is the act of using known statistical information and patterns about the plaintext to determine it. In cryptograms, each letter of the alphabet is encrypted to another letter. This table of letter-letter translations is what makes up the key. Because the letters are simply converted and nothing is scrambled, the cipher is left open to this sort of analysis; all we need is that ciphertext. If the attacker knows that the language used is English, for example, there are a great many patterns that can be searched for. Classic frequency analysis involves tallying up each letter in the collected ciphertext and comparing the percentages against the English language averages. If the letter "M" is most common then it is reasonable to guess that "E"-->"M" in the cipher because E is the most common letter in the English language.
    [Show full text]
  • Chap 2. Basic Encryption and Decryption
    Chap 2. Basic Encryption and Decryption H. Lee Kwang Department of Electrical Engineering & Computer Science, KAIST Objectives • Concepts of encryption • Cryptanalysis: how encryption systems are “broken” 2.1 Terminology and Background • Notations – S: sender – R: receiver – T: transmission medium – O: outsider, interceptor, intruder, attacker, or, adversary • S wants to send a message to R – S entrusts the message to T who will deliver it to R – Possible actions of O • block(interrupt), intercept, modify, fabricate • Chapter 1 2.1.1 Terminology • Encryption and Decryption – encryption: a process of encoding a message so that its meaning is not obvious – decryption: the reverse process • encode(encipher) vs. decode(decipher) – encoding: the process of translating entire words or phrases to other words or phrases – enciphering: translating letters or symbols individually – encryption: the group term that covers both encoding and enciphering 2.1.1 Terminology • Plaintext vs. Ciphertext – P(plaintext): the original form of a message – C(ciphertext): the encrypted form • Basic operations – plaintext to ciphertext: encryption: C = E(P) – ciphertext to plaintext: decryption: P = D(C) – requirement: P = D(E(P)) 2.1.1 Terminology • Encryption with key If the encryption algorithm should fall into the interceptor’s – encryption key: KE – decryption key: K hands, future messages can still D be kept secret because the – C = E(K , P) E interceptor will not know the – P = D(KD, E(KE, P)) key value • Keyless Cipher – a cipher that does not require the
    [Show full text]
  • John F. Byrne's Chaocipher Revealed
    John F. Byrne’s Chaocipher Revealed John F. Byrne’s Chaocipher Revealed: An Historical and Technical Appraisal MOSHE RUBIN1 Abstract Chaocipher is a method of encryption invented by John F. Byrne in 1918, who tried unsuccessfully to interest the US Signal Corp and Navy in his system. In 1953, Byrne presented Chaocipher-encrypted messages as a challenge in his autobiography Silent Years. Although numerous students of cryptanalysis attempted to solve the challenge messages over the years, none succeeded. For ninety years the Chaocipher algorithm was a closely guarded secret known only to a handful of persons. Following fruitful negotiations with the Byrne family during the period 2009-2010, the Chaocipher papers and materials have been donated to the National Cryptologic Museum in Ft. Meade, MD. This paper presents a comprehensive historical and technical evaluation of John F. Byrne and his Chaocipher system. Keywords ACA, American Cryptogram Association, block cipher encryption modes, Chaocipher, dynamic substitution, Greg Mellen, Herbert O. Yardley, John F. Byrne, National Cryptologic Museum, Parker Hitt, Silent Years, William F. Friedman 1 Introduction John Francis Byrne was born on 11 February 1880 in Dublin, Ireland. He was an intimate friend of James Joyce, the famous Irish writer and poet, studying together in Belvedere College and University College in Dublin. Joyce based the character named Cranly in Joyce’s A Portrait of the Artist as a Young Man on Byrne, used Byrne’s Dublin residence of 7 Eccles Street as the home of Leopold and Molly Bloom, the main characters in Joyce’s Ulysses, and made use of real-life anecdotes of himself and Byrne as the basis of stories in Ulysses.
    [Show full text]
  • Shift Cipher Substitution Cipher Vigenère Cipher Hill Cipher
    Lecture 2 Classical Cryptosystems Shift cipher Substitution cipher Vigenère cipher Hill cipher 1 Shift Cipher • A Substitution Cipher • The Key Space: – [0 … 25] • Encryption given a key K: – each letter in the plaintext P is replaced with the K’th letter following the corresponding number ( shift right ) • Decryption given K: – shift left • History: K = 3, Caesar’s cipher 2 Shift Cipher • Formally: • Let P=C= K=Z 26 For 0≤K≤25 ek(x) = x+K mod 26 and dk(y) = y-K mod 26 ʚͬ, ͭ ∈ ͔ͦͪ ʛ 3 Shift Cipher: An Example ABCDEFGHIJKLMNOPQRSTUVWXYZ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 • P = CRYPTOGRAPHYISFUN Note that punctuation is often • K = 11 eliminated • C = NCJAVZRCLASJTDQFY • C → 2; 2+11 mod 26 = 13 → N • R → 17; 17+11 mod 26 = 2 → C • … • N → 13; 13+11 mod 26 = 24 → Y 4 Shift Cipher: Cryptanalysis • Can an attacker find K? – YES: exhaustive search, key space is small (<= 26 possible keys). – Once K is found, very easy to decrypt Exercise 1: decrypt the following ciphertext hphtwwxppelextoytrse Exercise 2: decrypt the following ciphertext jbcrclqrwcrvnbjenbwrwn VERY useful MATLAB functions can be found here: http://www2.math.umd.edu/~lcw/MatlabCode/ 5 General Mono-alphabetical Substitution Cipher • The key space: all possible permutations of Σ = {A, B, C, …, Z} • Encryption, given a key (permutation) π: – each letter X in the plaintext P is replaced with π(X) • Decryption, given a key π: – each letter Y in the ciphertext C is replaced with π-1(Y) • Example ABCDEFGHIJKLMNOPQRSTUVWXYZ πBADCZHWYGOQXSVTRNMSKJI PEFU • BECAUSE AZDBJSZ 6 Strength of the General Substitution Cipher • Exhaustive search is now infeasible – key space size is 26! ≈ 4*10 26 • Dominates the art of secret writing throughout the first millennium A.D.
    [Show full text]
  • Applications of Search Techniques to Cryptanalysis and the Construction of Cipher Components. James David Mclaughlin Submitted F
    Applications of search techniques to cryptanalysis and the construction of cipher components. James David McLaughlin Submitted for the degree of Doctor of Philosophy (PhD) University of York Department of Computer Science September 2012 2 Abstract In this dissertation, we investigate the ways in which search techniques, and in particular metaheuristic search techniques, can be used in cryptology. We address the design of simple cryptographic components (Boolean functions), before moving on to more complex entities (S-boxes). The emphasis then shifts from the construction of cryptographic arte- facts to the related area of cryptanalysis, in which we first derive non-linear approximations to S-boxes more powerful than the existing linear approximations, and then exploit these in cryptanalytic attacks against the ciphers DES and Serpent. Contents 1 Introduction. 11 1.1 The Structure of this Thesis . 12 2 A brief history of cryptography and cryptanalysis. 14 3 Literature review 20 3.1 Information on various types of block cipher, and a brief description of the Data Encryption Standard. 20 3.1.1 Feistel ciphers . 21 3.1.2 Other types of block cipher . 23 3.1.3 Confusion and diffusion . 24 3.2 Linear cryptanalysis. 26 3.2.1 The attack. 27 3.3 Differential cryptanalysis. 35 3.3.1 The attack. 39 3.3.2 Variants of the differential cryptanalytic attack . 44 3.4 Stream ciphers based on linear feedback shift registers . 48 3.5 A brief introduction to metaheuristics . 52 3.5.1 Hill-climbing . 55 3.5.2 Simulated annealing . 57 3.5.3 Memetic algorithms . 58 3.5.4 Ant algorithms .
    [Show full text]
  • Substitution Ciphers
    Foundations of Computer Security Lecture 40: Substitution Ciphers Dr. Bill Young Department of Computer Sciences University of Texas at Austin Lecture 40: 1 Substitution Ciphers Substitution Ciphers A substitution cipher is one in which each symbol of the plaintext is exchanged for another symbol. If this is done uniformly this is called a monoalphabetic cipher or simple substitution cipher. If different substitutions are made depending on where in the plaintext the symbol occurs, this is called a polyalphabetic substitution. Lecture 40: 2 Substitution Ciphers Simple Substitution A simple substitution cipher is an injection (1-1 mapping) of the alphabet into itself or another alphabet. What is the key? A simple substitution is breakable; we could try all k! mappings from the plaintext to ciphertext alphabets. That’s usually not necessary. Redundancies in the plaintext (letter frequencies, digrams, etc.) are reflected in the ciphertext. Not all substitution ciphers are simple substitution ciphers. Lecture 40: 3 Substitution Ciphers Caesar Cipher The Caesar Cipher is a monoalphabetic cipher in which each letter is replaced in the encryption by another letter a fixed “distance” away in the alphabet. For example, A is replaced by C, B by D, ..., Y by A, Z by B, etc. What is the key? What is the size of the keyspace? Is the algorithm strong? Lecture 40: 4 Substitution Ciphers Vigen`ere Cipher The Vigen`ere Cipher is an example of a polyalphabetic cipher, sometimes called a running key cipher because the key is another text. Start with a key string: “monitors to go to the bathroom” and a plaintext to encrypt: “four score and seven years ago.” Align the two texts, possibly removing spaces: plaintext: fours corea ndsev enyea rsago key: monit orsto gotot hebat hroom ciphertext: rcizl qfkxo trlso lrzet yjoua Then use the letter pairs to look up an encryption in a table (called a Vigen`ere Tableau or tabula recta).
    [Show full text]