DOCSLIB.ORG

Derivatives Markets the Pearson Series in Finance

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Derivatives Markets the Pearson Series in Finance Derivatives Markets The Pearson Series in Finance Bekaert/Hodrick Hull International Financial Management Fundamentals of Futures and Options Markets Berk/DeMarzo Hull Corporate Finance* Options, Futures, and Other Derivatives Berk/DeMarzo Keown Corporate Finance: The Core* Personal Finance: Turning Money into Wealth* Berk/DeMarzo/Harford Keown/Martin/Petty Fundamentals of Corporate Finance* Foundations of Finance: The Logic and Practice of Financial Management* Brooks Financial Management: Core Concepts* Kim/Nofsinger Corporate Governance Copeland/Weston/Shastri Financial Theory and Corporate Policy Madura Personal Finance* Dorfman/Cather Introduction to Risk Management and Insurance Marthinsen Risk Takers: Uses and Abuses of Financial Derivatives Eiteman/Stonehill/Moffett Multinational Business Finance McDonald Derivatives Markets Fabozzi Bond Markets: Analysis and Strategies McDonald Fundamentals of Derivatives Markets Fabozzi/Modigliani Capital Markets: Institutions and Instruments Mishkin/Eakins Financial Markets and Institutions Fabozzi/Modigliani/Jones Foundations of Financial Markets and Institutions Moffett/Stonehill/Eiteman Fundamentals of Multinational Finance Finkler Financial Management for Public, Health, and Nofsinger Not-for-Profit Organizations Psychology of Investing Frasca Ormiston/Fraser Personal Finance Understanding Financial Statements Gitman/Joehnk/Smart Pennacchi Fundamentals of Investing* Theory of Asset Pricing Gitman/Zutter Rejda Principles of Managerial Finance* Principles of Risk Management and Insurance Gitman/Zutter Seiler Principles of Managerial Finance—Brief Edition* Performing Financial Studies: A Methodological Cookbook Haugen The Inefficient Stock Market: What Pays Off and Why Solnik/McLeavey Global Investments Haugen The New Finance: Overreaction, Complexity, and Stretcher/Michael Uniqueness Cases in Financial Management Holden Titman/Keown/Martin Excel Modeling in Corporate Finance Financial Management: Principles and Applications* Holden Titman/Martin Excel Modeling in Investments Valuation: The Art and Science of Corporate Investment Decisions Hughes/MacDonald International Banking: Text and Cases Weston/Mitchel/Mulherin Takeovers, Restructuring, and Corporate Governance * denotes MyFinanceLab titles Log onto www.myfinancelab.com to learn more Derivatives Markets THIRD EDITION Robert L. McDonald Northwestern University Kellogg School of Management Boston Columbus Indianapolis New York San Francisco Upper Saddle River Amsterdam Cape Town Dubai London Madrid Milan Munich Paris Montreal Toronto Delhi Mexico City Sao Paulo Sydney Hong Kong Seoul Singapore Taipei Tokyo Editor in Chief: Donna Battista Cover Designer: Bruce Kenselaar Acquisitions Editor: Katie Rowland Creative Director: Jayne Conte Editorial Project Manager: Jill Kolongowski Cover Art: Shutterstock/Pokaz Editorial Assistant: Elissa Senra-Sargent Media Director: Susan Schoenberg Director of Marketing: Maggie Moylan Media Project Manager: Lisa Rinaldi Marketing Manager: Jami Minard Supplements Editors: Kathryn Dinovo, Alison Eusden Director of Production: Erin Gregg Full-Service Project Management: Cypress Graphics, Senior Managing Editor: Nancy Fenton Windfall Software Production Project Manager: Carla Thompson Printer/Binder: Edwards Brothers Senior Manufacturing Buyer: Carol Melville Cover Printer: Lehigh-Phoenix Color/Hagerstown Text Designer: Gina Hagen Kolenda Text Font: Times Roman Credits and acknowledgments borrowed from other sources and reproduced, with permission, in this textbook appear on the appropriate page within text. Microsoft and/or its respective suppliers make no representations about the suitability of the information contained in the documents and related graphics published as part of the services for any purpose. All such documents and related graphics are provided "as is" without warranty of any kind. Microsoft and/or its respective suppliers hereby disclaim all warranties and conditions with regard to this information, including all warranties and conditions of merchantability, whether express, implied or statutory, fitness for a particular purpose, title and non-infringement. In no event shall Microsoft and/or its respective suppliers be liable for any special, indirect or consequential damages or any damages whatsoever resulting from loss of use, data or profits, whether in an action of contract, negligence or other tortious action, arising out of or in connection with the use or performance of information available from the services. The documents and related graphics contained herein could include technical inaccuracies or typographical errors. Changes are periodically added to the information herein. Microsoft and/or its respective suppliers may make improvements and/or changes in the product(s) and/or the program(s) described herein at any time. Partial screen shots may be viewed in full within the software version specified. Microsoft® and Windows® are registered trademarks of the Microsoft Corporation in the U.S.A. and other countries. Screen shots and icons reprinted with permission from the Microsoft Corporation. This book is not sponsored or endorsed by or affiliated with the Microsoft Corporation. Copyright © 2013, 2006, 2003 by Pearson Education, Inc., publishing as Prentice Hall. All rights reserved. Manufactured in the United States of America. This publication is protected by Copyright, and permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. To obtain permission(s) to use material from this work, please submit a written request to Pearson Education, Inc., Permissions Department, One Lake Street, Upper Saddle River, New Jersey 07458, or you may fax your request to 201-236-3290. Many of the designations by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and the publisher was aware of a trademark claim, the designations have been printed in initial caps or all caps. Library of Congress Cataloging-in-Publication Data McDonald, Robert L. (Robert Lynch) Derivatives markets / Robert L. McDonald. — 3rd ed. p. cm. Includes bibliographical references and index. ISBN-13: 978-0-321-54308-0 (hardcover) ISBN-10: 0-321-54308-4 (hardcover) 1. Derivative securities. I. Title. HG6024.A3M394 2013 332.6457—dc23 2012029875 10987654321 ISBN 10: 0-321-54308-4 ISBN 13: 978-0-321-54308-0 For Irene, Claire, David, and Henry This page intentionally left blank Brief Contents Preface xxi 1 Introduction to Derivatives 1 PART ONE Insurance, Hedging, and Simple Strategies 23 2 An Introduction to Forwards and Options 25 3 Insurance, Collars, and Other Strategies 61 4 Introduction to Risk Management 89 PART TWO Forwards, Futures, and Swaps 123 5 Financial Forwards and Futures 125 6 Commodity Forwards and Futures 163 7 Interest Rate Forwards and Futures 195 8 Swaps 233 PART THREE Options 263 9 Parity and Other Option Relationships 265 10 Binomial Option Pricing: Basic Concepts 293 11 Binomial Option Pricing: Selected Topics 323 12 The Black-Scholes Formula 349 13 Market-Making and Delta-Hedging 381 14 Exotic Options: I 409 vii viii Brief Contents PART FOUR Financial Engineering and Applications 435 15 Financial Engineering and Security Design 437 16 Corporate Applications 469 17 Real Options 509 PART FIVE Advanced Pricing Theory and Applications 543 18 The Lognormal Distribution 545 19 Monte Carlo Valuation 573 20 Brownian Motion and Ito’sˆ Lemma 603 21 The Black-Scholes-Merton Equation 627 22 Risk-Neutral and Martingale Pricing 649 23 Exotic Options: II 683 24 Volatility 717 25 Interest Rate and Bond Derivatives 751 26 Value at Risk 789 27 Credit Risk 815 Appendix A The Greek Alphabet 851 Appendix B Continuous Compounding 853 Appendix C Jensen’s Inequality 859 Appendix D An Introduction to Visual Basic for Applications 863 Glossary 883 References 897 Index 915 Contents Preface xxi PART ONE Insurance, Hedging, and Simple Chapter 1 Strategies 23 Introduction to Derivatives 1 1.1 What Is a Derivative? 2 Chapter 2 1.2 An Overview of Financial Markets 2 An Introduction to Forwards and Trading of Financial Assets 2 Options 25 Measures of Market Size and Activity 4 2.1 Forward Contracts 25 Stock and Bond Markets 5 The Payoff on a Forward Contract 29 Derivatives Markets 6 Graphing the Payoff on a Forward 1.3 The Role of Financial Markets 9 Contract 30 Financial Markets and the Averages 9 Comparing a Forward and Outright Risk-Sharing 10 Purchase 30 1.4 The Uses of Derivatives 11 Zero-Coupon Bonds in Payoff and Profit Uses of Derivatives 11 Diagrams 33 Perspectives on Derivatives 13 Cash Settlement Versus Delivery 34 Financial Engineering and Security Credit Risk 34 Design 14 2.2 Call Options 35 1.5 Buying and Short-Selling Financial Option Terminology 35 Assets 14 Payoff and Profit for a Purchased Call Transaction Costs and the Bid-Ask Option 36 Spread 14 Payoff and Profit for a Written Call Ways to Buy or Sell 15 Option 38 Short-Selling 16 2.3 Put Options 41 The Lease Rate of an Asset 18 Payoff and Profit for a Purchased Put Risk and Scarcity in Short-Selling 18 Option 41 Chapter Summary 20 Payoff and Profit for a Written Put Further Reading 20 Option 42 Problems 20 The “Moneyness” of an Option 44 ix x Contents 2.4 Summary of Forward and Option Chapter 4 Positions 45 Introduction to Risk Management 89 Positions Long with Respect to the 4.1 Basic Risk Management: The Producer’s Index
Load more

Recommended publications
  • The Turtle Becomes the Hare the Implications of Artificial Short-Termism for Climate Finance
    THE TURTLE BECOMES THE HARE THE IMPLICATIONS OF ARTIFICIAL SHORT-TERMISM FOR CLIMATE FINANCE DISCUSSION PAPER – OCTOBER 2014 1. INTRODUCTION 2°INVESTING INITIATIVE A growing narra@ve arounD short-termism. A The 2° Inves@ng Ini@ave [2°ii] is a growing chorus of voices have argued that the mul-stakeholder think tank finance sector suffers from ‘short-termism’ – working to align the financial sector focusing on short-term risks and benefits at the with 2°C climate goals. Our research expense of long-term risk-return op@mizaon. and advocacy work seeks to: While the academic literature behind this narrave • Align investment processes of financial instuons with 2°C has enjoyed a renaissance since the 1990s, the climate scenarios; global financial crisis and its aermath triggered a • Develop the metrics and tools to new focus on the issue, by academics, measure the climate performance of policymakers, and financial ins@tu@ons themselves. financial ins@tu@ons; • Mobilize regulatory and policy Impact of short-termism. The new focus has placed incen@ves to shiJ capital to energy par@cular emphasis on short-termism as a cause of transi@on financing. the global financial crisis. In this role, short-termism is seen to have taken long-term (or even medium- The associaon was founded in term) risks off the radar screen. Short-termism is 2012 in Paris and has projects in Europe, China and the US. Our work also blamed for models that extrapolated beyond is global, both in terms of geography short-term factors and were built with limited and engaging key actors.
    [Show full text]
  • The TIPS-Treasury Bond Puzzle
    The TIPS-Treasury Bond Puzzle Matthias Fleckenstein, Francis A. Longstaff and Hanno Lustig The Journal of Finance, October 2014 Presented By: Rafael A. Porsani The TIPS-Treasury Bond Puzzle 1 / 55 Introduction The TIPS-Treasury Bond Puzzle 2 / 55 Introduction (1) Treasury bond and the Treasury Inflation-Protected Securities (TIPS) markets: two of the largest and most actively traded fixed-income markets in the world. Find that there is persistent mispricing on a massive scale across them. Treasury bonds are consistently overpriced relative to TIPS. Price of a Treasury bond can exceed that of an inflation-swapped TIPS issue exactly matching the cash flows of the Treasury bond by more than $20 per $100 notional amount. One of the largest examples of arbitrage ever documented. The TIPS-Treasury Bond Puzzle 3 / 55 Introduction (2) Use TIPS plus inflation swaps to create synthetic Treasury bond. Price differences between the synthetic Treasury bond and the nominal Treasury bond: arbitrage opportunities. Average size of the mispricing: 54.5 basis points, but can exceed 200 basis points for some pairs. I The average size of this mispricing is orders of magnitude larger than transaction costs. The TIPS-Treasury Bond Puzzle 4 / 55 Introduction (3) What drives the mispricing? Slow-moving capital may help explain why mispricing persists. Is TIPS-Treasury mispricing related to changes in capital available to hedge funds? Answer: Yes. Mispricing gets smaller as more capital gets to the hedge fund sector. The TIPS-Treasury Bond Puzzle 5 / 55 Introduction (4) Also find that: Correlation in arbitrage strategies: size of TIPS-Treasury arbitrage is correlated with arbitrage mispricing in other markets.
    [Show full text]
  • Schedule Rc-L – Derivatives and Off-Balance Sheet Items
    FFIEC 031 and 041 RC-L – DERIVATIVES AND OFF-BALANCE SHEET SCHEDULE RC-L – DERIVATIVES AND OFF-BALANCE SHEET ITEMS General Instructions Schedule RC-L should be completed on a fully consolidated basis. In addition to information about derivatives, Schedule RC-L includes the following selected commitments, contingencies, and other off-balance sheet items that are not reportable as part of the balance sheet of the Report of Condition (Schedule RC). Among the items not to be reported in Schedule RC-L are contingencies arising in connection with litigation. For those asset-backed commercial paper program conduits that the reporting bank consolidates onto its balance sheet (Schedule RC) in accordance with ASC Subtopic 810-10, Consolidation – Overall (formerly FASB Interpretation No. 46 (Revised), “Consolidation of Variable Interest Entities,” as amended by FASB Statement No. 167, “Amendments to FASB Interpretation No. 46(R)”), any credit enhancements and liquidity facilities the bank provides to the programs should not be reported in Schedule RC-L. In contrast, for conduits that the reporting bank does not consolidate, the bank should report the credit enhancements and liquidity facilities it provides to the programs in the appropriate items of Schedule RC-L. Item Instructions Item No. Caption and Instructions 1 Unused commitments. Report in the appropriate subitem the unused portions of commitments. Unused commitments are to be reported gross, i.e., include in the appropriate subitem the unused amount of commitments acquired from and conveyed or participated to others. However, exclude commitments conveyed or participated to others that the bank is not legally obligated to fund even if the party to whom the commitment has been conveyed or participated fails to perform in accordance with the terms of the commitment.
    [Show full text]
  • Lecture 7 Futures Markets and Pricing
    Lecture 7 Futures Markets and Pricing Prof. Paczkowski Lecture 7 Futures Markets and Pricing Prof. Paczkowski Rutgers University Spring Semester, 2009 Prof. Paczkowski (Rutgers University) Lecture 7 Futures Markets and Pricing Spring Semester, 2009 1 / 65 Lecture 7 Futures Markets and Pricing Prof. Paczkowski Part I Assignment Prof. Paczkowski (Rutgers University) Lecture 7 Futures Markets and Pricing Spring Semester, 2009 2 / 65 Assignment Lecture 7 Futures Markets and Pricing Prof. Paczkowski Prof. Paczkowski (Rutgers University) Lecture 7 Futures Markets and Pricing Spring Semester, 2009 3 / 65 Lecture 7 Futures Markets and Pricing Prof. Paczkowski Introduction Part II Background Financial Markets Forward Markets Introduction Futures Markets Roles of Futures Markets Existence Roles of Futures Markets Futures Contracts Terminology Prof. Paczkowski (Rutgers University) Lecture 7 Futures Markets and Pricing Spring Semester, 2009 4 / 65 Pricing Incorporating Risk Profiting and Offsetting Futures Concept Lecture 7 Futures Markets and Buyer Seller Pricing Wants to buy Prof. Paczkowski Situation - but not today Introduction Price will rise Background Expectation before ready Financial Markets to buy Forward Markets 1 Futures Markets Buy today Roles of before ready Futures Markets Strategy 2 Buy futures Existence contract to Roles of Futures hedge losses Markets Locks in low Result Futures price Contracts Terminology Prof. Paczkowski (Rutgers University) Lecture 7 Futures Markets and Pricing Spring Semester, 2009 5 / 65 Pricing Incorporating
    [Show full text]
  • Derivative Markets Swaps.Pdf
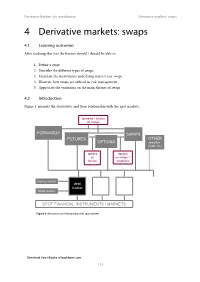
    Derivative Markets: An Introduction Derivative markets: swaps 4 Derivative markets: swaps 4.1 Learning outcomes After studying this text the learner should / should be able to: 1. Define a swap. 2. Describe the different types of swaps. 3. Elucidate the motivations underlying interest rate swaps. 4. Illustrate how swaps are utilised in risk management. 5. Appreciate the variations on the main themes of swaps. 4.2 Introduction Figure 1 presentsFigure the derivatives 1: derivatives and their relationshipand relationship with the spotwith markets. spot markets forwards / futures on swaps FORWARDS SWAPS FUTURES OTHER OPTIONS (weather, credit, etc) options options on on swaps = futures swaptions money market debt equity forex commodity market market market markets bond market SPOT FINANCIAL INSTRUMENTS / MARKETS Figure 1: derivatives and relationship with spot markets Download free eBooks at bookboon.com 116 Derivative Markets: An Introduction Derivative markets: swaps Swaps emerged internationally in the early eighties, and the market has grown significantly. An attempt was made in the early eighties in some smaller to kick-start the interest rate swap market, but few money market benchmarks were available at that stage to underpin this new market. It was only in the middle nineties that the swap market emerged in some of these smaller countries, and this was made possible by the creation and development of acceptable benchmark money market rates. The latter are critical for the development of the derivative markets. We cover swaps before options because of the existence of options on swaps. This illustration shows that we find swaps in all the spot financial markets. A swap may be defined as an agreement between counterparties (usually two but there can be more 360° parties involved in some swaps) to exchange specific periodic cash flows in the future based on specified prices / interest rates.
    [Show full text]
  • Is the International Role of the Dollar Changing?
    Is the International Role of the Dollar Changing? Linda S. Goldberg Recently the U.S. dollar’s preeminence as an international currency has been questioned. The emergence of the euro, changes www.newyorkfed.org/research/current_issues ✦ in the dollar’s value, and the fi nancial market crisis have, in the view of many commentators, posed a signifi cant challenge to the currency’s long-standing position in world markets. However, a study of the dollar across critical areas of international trade January 2010 ✦ and fi nance suggests that the dollar has retained its standing in key roles. While changes in the global status of the dollar are possible, factors such as inertia in currency use, the large size and relative stability of the U.S. economy, and the dollar pricing of oil and other commodities will help perpetuate the dollar’s role as the dominant medium for international transactions. Volume 16, Number 1 Volume y many measures, the U.S. dollar is the most important currency in the world. IN ECONOMICS AND FINANCE It plays a central role in international trade and fi nance as both a store of value Band a medium of exchange. Many countries have adopted an exchange rate regime that anchors the value of their home currency to that of the dollar. Dollar holdings fi gure prominently in offi cial foreign exchange (FX) reserves—the foreign currency deposits and bonds maintained by monetary authorities and governments. And in international trade, the dollar is widely used for invoicing and settling import and export transactions around the world.
    [Show full text]
  • How Much Do Banks Use Credit Derivatives to Reduce Risk?
    How much do banks use credit derivatives to reduce risk? Bernadette A. Minton, René Stulz, and Rohan Williamson* June 2006 This paper examines the use of credit derivatives by US bank holding companies from 1999 to 2003 with assets in excess of one billion dollars. Using the Federal Reserve Bank of Chicago Bank Holding Company Database, we find that in 2003 only 19 large banks out of 345 use credit derivatives. Though few banks use credit derivatives, the assets of these banks represent on average two thirds of the assets of bank holding companies with assets in excess of $1 billion. To the extent that banks have positions in credit derivatives, they tend to be used more for dealer activities than for hedging activities. Nevertheless, a majority of the banks that use credit derivative are net buyers of credit protection. Banks are more likely to be net protection buyers if they engage in asset securitization, originate foreign loans, and have lower capital ratios. The likelihood of a bank being a net protection buyer is positively related to the percentage of commercial and industrial loans in a bank’s loan portfolio and negatively or not related to other types of bank loans. The use of credit derivatives by banks is limited because adverse selection and moral hazard problems make the market for credit derivatives illiquid for the typical credit exposures of banks. *Respectively, Associate Professor, The Ohio State University; Everett D. Reese Chair of Banking and Monetary Economics, The Ohio State University and NBER; and Associate Professor, Georgetown University. We are grateful to Jim O’Brien and Mark Carey for discussions.
    [Show full text]
  • An Asset Manager's Guide to Swap Trading in the New Regulatory World
    CLIENT MEMORANDUM An Asset Manager’s Guide to Swap Trading in the New Regulatory World March 11, 2013 As a result of the Dodd-Frank Act, the over-the-counter derivatives markets Contents have become subject to significant new regulatory oversight. As the Swaps, Security-Based markets respond to these new regulations, the menu of derivatives Swaps, Mixed Swaps and Excluded Instruments ................. 2 instruments available to asset managers, and the costs associated with those instruments, will change significantly. As the first new swap rules Key Market Participants .............. 4 have come into effect in the past several months, market participants have Cross-Border Application of started to identify risks and costs, as well as new opportunities, arising from the U.S. Swap Regulatory this new regulatory landscape. Regime ......................................... 7 Swap Reporting ........................... 8 This memorandum is designed to provide asset managers with background information on key aspects of the swap regulatory regime that may impact Swap Clearing ............................ 12 their derivatives trading activities. The memorandum focuses largely on the Swap Trading ............................. 15 regulations of the CFTC that apply to swaps, rather than on the rules of the Uncleared Swap Margin ............ 16 SEC that will govern security-based swaps, as virtually none of the SEC’s security-based swap rules have been adopted. Swap Dealer Business Conduct and Swap This memorandum first provides background information on the types of Documentation Rules ................ 19 derivatives that are subject to the CFTC’s swap regulatory regime, on new Position Limits and Large classifications of market participants created by the regime, and on the Trader Reporting ....................... 22 current approach to the cross-border application of swap requirements.
    [Show full text]
  • Implied Volatility Modeling
    Implied Volatility Modeling Sarves Verma, Gunhan Mehmet Ertosun, Wei Wang, Benjamin Ambruster, Kay Giesecke I Introduction Although Black-Scholes formula is very popular among market practitioners, when applied to call and put options, it often reduces to a means of quoting options in terms of another parameter, the implied volatility. Further, the function σ BS TK ),(: ⎯⎯→ σ BS TK ),( t t ………………………………(1) is called the implied volatility surface. Two significant features of the surface is worth mentioning”: a) the non-flat profile of the surface which is often called the ‘smile’or the ‘skew’ suggests that the Black-Scholes formula is inefficient to price options b) the level of implied volatilities changes with time thus deforming it continuously. Since, the black- scholes model fails to model volatility, modeling implied volatility has become an active area of research. At present, volatility is modeled in primarily four different ways which are : a) The stochastic volatility model which assumes a stochastic nature of volatility [1]. The problem with this approach often lies in finding the market price of volatility risk which can’t be observed in the market. b) The deterministic volatility function (DVF) which assumes that volatility is a function of time alone and is completely deterministic [2,3]. This fails because as mentioned before the implied volatility surface changes with time continuously and is unpredictable at a given point of time. Ergo, the lattice model [2] & the Dupire approach [3] often fail[4] c) a factor based approach which assumes that implied volatility can be constructed by forming basis vectors. Further, one can use implied volatility as a mean reverting Ornstein-Ulhenbeck process for estimating implied volatility[5].
    [Show full text]
  • 2017 Financial Services Industry Outlook
    NEW YORK 535 Madison Avenue, 19th Floor New York, NY 10022 +1 212 207 1000 SAN FRANCISCO One Market Street, Spear Tower, Suite 3600 San Francisco, CA 94105 +1 415 293 8426 DENVER 999 Eighteenth Street, Suite 3000 2017 Denver, CO 80202 FINANCIAL SERVICES +1 303 893 2899 INDUSTRY REVIEW MEMBER, FINRA / SIPC SYDNEY Level 2, 9 Castlereagh Street Sydney, NSW, 2000 +61 419 460 509 BERKSHIRE CAPITAL SECURITIES LLC (ARBN 146 206 859) IS A LIMITED LIABILITY COMPANY INCORPORATED IN THE UNITED STATES AND REGISTERED AS A FOREIGN COMPANY IN AUSTRALIA UNDER THE CORPORATIONS ACT 2001. BERKSHIRE CAPITAL IS EXEMPT FROM THE REQUIREMENTS TO HOLD AN AUSTRALIAN FINANCIAL SERVICES LICENCE UNDER THE AUSTRALIAN CORPORATIONS ACT IN RESPECT OF THE FINANCIAL SERVICES IT PROVIDES. BERKSHIRE CAPITAL IS REGULATED BY THE SEC UNDER US LAWS, WHICH DIFFER FROM AUSTRALIAN LAWS. LONDON 11 Haymarket, 2nd Floor London, SW1Y 4BP United Kingdom +44 20 7828 2828 BERKSHIRE CAPITAL SECURITIES LIMITED IS AUTHORISED AND REGULATED BY THE FINANCIAL CONDUCT AUTHORITY (REGISTRATION NUMBER 188637). www.berkcap.com CONTENTS ABOUT BERKSHIRE CAPITAL Summary 1 Berkshire Capital is an independent employee-owned investment bank specializing in M&A in the financial services sector. With more completed transactions in this space than any Traditional Investment Management 6 other investment bank, we help clients find successful, long-lasting partnerships. Wealth Management 9 Founded in 1983, Berkshire Capital is headquartered in New York with partners located in Cross Border 13 London, Sydney, San Francisco, Denver and Philadelphia. Our partners have been with the firm an average of 14 years. We are recognized as a leading expert in the asset management, Real Estate 17 wealth management, alternatives, real estate and broker/dealer industries.
    [Show full text]
  • Shadow Banking
    Federal Reserve Bank of New York Staff Reports Shadow Banking Zoltan Pozsar Tobias Adrian Adam Ashcraft Hayley Boesky Staff Report No. 458 July 2010 Revised February 2012 FRBNY Staff REPORTS This paper presents preliminary findings and is being distributed to economists and other interested readers solely to stimulate discussion and elicit comments. The views expressed in this paper are those of the authors and are not necessar- ily reflective of views at the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the authors. Shadow Banking Zoltan Pozsar, Tobias Adrian, Adam Ashcraft, and Hayley Boesky Federal Reserve Bank of New York Staff Reports, no. 458 July 2010: revised February 2012 JEL classification: G20, G28, G01 Abstract The rapid growth of the market-based financial system since the mid-1980s changed the nature of financial intermediation. Within the market-based financial system, “shadow banks” have served a critical role. Shadow banks are financial intermediaries that con- duct maturity, credit, and liquidity transformation without explicit access to central bank liquidity or public sector credit guarantees. Examples of shadow banks include finance companies, asset-backed commercial paper (ABCP) conduits, structured investment vehicles (SIVs), credit hedge funds, money market mutual funds, securities lenders, limited-purpose finance companies (LPFCs), and the government-sponsored enterprises (GSEs). Our paper documents the institutional features of shadow banks, discusses their economic roles, and analyzes their relation to the traditional banking system. Our de- scription and taxonomy of shadow bank entities and shadow bank activities are accom- panied by “shadow banking maps” that schematically represent the funding flows of the shadow banking system.
    [Show full text]
  • Tax Treatment of Derivatives
    United States Viva Hammer* Tax Treatment of Derivatives 1. Introduction instruments, as well as principles of general applicability. Often, the nature of the derivative instrument will dictate The US federal income taxation of derivative instruments whether it is taxed as a capital asset or an ordinary asset is determined under numerous tax rules set forth in the US (see discussion of section 1256 contracts, below). In other tax code, the regulations thereunder (and supplemented instances, the nature of the taxpayer will dictate whether it by various forms of published and unpublished guidance is taxed as a capital asset or an ordinary asset (see discus- from the US tax authorities and by the case law).1 These tax sion of dealers versus traders, below). rules dictate the US federal income taxation of derivative instruments without regard to applicable accounting rules. Generally, the starting point will be to determine whether the instrument is a “capital asset” or an “ordinary asset” The tax rules applicable to derivative instruments have in the hands of the taxpayer. Section 1221 defines “capital developed over time in piecemeal fashion. There are no assets” by exclusion – unless an asset falls within one of general principles governing the taxation of derivatives eight enumerated exceptions, it is viewed as a capital asset. in the United States. Every transaction must be examined Exceptions to capital asset treatment relevant to taxpayers in light of these piecemeal rules. Key considerations for transacting in derivative instruments include the excep- issuers and holders of derivative instruments under US tions for (1) hedging transactions3 and (2) “commodities tax principles will include the character of income, gain, derivative financial instruments” held by a “commodities loss and deduction related to the instrument (ordinary derivatives dealer”.4 vs.
    [Show full text]