DOCSLIB.ORG

The Leaky Bucket As a Policing Device: Transient Analysis and Dimensioning 1 Introduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Leaky Bucket As a Policing Device: Transient Analysis and Dimensioning 1 Introduction The Leaky Bucket as a Policing Device Transient Analysis and Dimensioning y Dimitris Logothetis Kishor Trivedi Center for Advanced Computing Comm GTE Lab oratories Inc Department of Electrical Engineering Sylvan Rd DukeUniversityBox Waltham MA Durham NC Abstract Policing the mechanism that the network uses to ensure that the user conforms with his negotiated contract is an imp ortant asp ect of the forthcoming broadband networks based on ATM The leaky bucket algorithm has b een adopted by ITU for merly CCITT as the means to p olice ATM connections The p erformance of the leaky bucket ie howwell can the leaky bucket algorithm enforce the parameters of the negotiated contract is a topic of ma jor interest In this pap er we derive expressions for the timedep endent state probabilities and the timeaveraged stateprobabilities for the leaky bucket rate control scheme Our mo del is based on the theory of Markov regenerative pro cesses In particular we show that the leaky bucket state probabil ities are p erio dic when studied in continuous time We also compute timeaveraged measures and show that our results sp ecialize to those obtained bySidi et al for the longrun b ehavior of leaky bucket Our results are more general however in that they apply to the transient regime and to more general arrival pro cesses Finallyusing our timedep endent analysis we dimension the leaky bucket parameters and quantify tradeos on these Intro duction Due to ATMs inherent prop erty to supp ort any bandwidth requirement an access control scheme is needed to ensure that a user do es not exceed his negotiated parameters One asp ect of Usage Network Parameter Control UPCNPC is p olicing The role of p olicing Part of this pap er has app eared in the Pro ceedings of INFOCOM y This work was supp orted in part by the National Science Foundation under Grant EEC is to ensure that nonconforming cells are marked as low priority cells or they are lost ITU formerly CCITT has standardized two equivalentmechanisms for p olicing one of them b eing the leaky bucket In this pap er we will present the timedep endent analysis of the leaky bucket for general p oint arrival pro cesses In contrast to previous works we allowfor nonstationary arrival pro cesses ie pro cesses where their parameters change over time since such pro cesses can capture overload b ehavior Wewillshow that the state distribution of the leaky bucket when studied in continuous time and assuming a p oint pro cess as general as the BatchMarkovian Arrival Pro cess BMAP is p erio dic This b ehavior although rep orted earlier is not widely known We then compute the timeaveraged state distribution and show that its limits exist Since we treat the leaky bucket as a p olicing mechanism ie as a mechanism to lter incoming trac we concentrate on loss measures Weidentify twotyp es of loss measures The rst one that we will refer to as tagged cell loss is dened as the probability that an incoming cell is lost or marked with low priority As we shall see later this measure p ossesses a p erio dic limiting b ehavior The other one that we will refer to as fractional loss is dened as ratio of the exp ected numb er of lost cells over the exp ected numb er of arrived cells in a given interval of length tWe shall see that this measure has a limiting distribution Despite the fact that ITU has standardized only p eak rate as a trac descriptor the ATM Forum considers two other optional trac descriptors namely burst tolerance or p eak rate duration and sustainable cell rate or mean rate The second part of the pap er will b e devoted to dimensioning the leaky bucket enforcing trac parameters such as p eak rate mean rate and p eak rate duration The mathematical to ol that we use is called the Markov regenerative or semiregenerative pro cess The remaining of the pap er is organized as follows In Section we describ e the leaky bucket rate control scheme and present the necessary background on Markov regenerative pro cesses and the BMAP pro cess In Section wedevelop the mo del based on the BMAP input pro cess while in Section we present the mo del for nonstationary input pro cesses and study the overload b ehavior of the leaky bucket In Section we study the abilityof the leaky bucket to control the desired trac parameters Finally in Section we present our conclusions Background In this section we review existing work in the analysis of the leaky bucket rate control scheme and wepresent some mathematical preliminaries needed to study the timedep endent b ehavior of the leaky bucket namely the delayed Markov regenerative theory and the batch Markovian arrival pro cess Fractional loss directly related to the cell loss ratio CLR Quality of Service QoS parameter of ATM is probably more suitable for dimensioning but more dicult to compute when compared with the tagged cell loss The Leaky Bucket Rate Control Scheme In high sp eed networks conventional windowow control is not feasible since propagation delays are the dominating factor in overall delay rather than transmission or queueing delays In simple words if we force the transmitter to wait for an acknowledgmentwe will force it to remain idle for a long p erio d of time since a time equal to the roundtrip delay elapses b efore a new message can b e transmitted For this reason alternativeschemes for owcontrol need to b e found One of these is the so called ratecontrol scheme where the arrival rate to a buer is ltered through a p olicing device One such device is the leaky bucket rate control scheme The leaky bucket see Figure consists of a token generator a p o ol of tokens and an optional buer Tokens are generated every seconds and stored in the p o ol if the p o ol contains less than L tokens Otherwise the token is lost Packetscells arrive to the buer according to a trac pro cess that needs to b e controlled The arrival pro cess can b e as general as the BatchMarkovian Arrival Pro cess BMAP although most of our numerical investigations consider sp ecial cases of the BMAP suchasMarkov Mo dulated Poisson Pro cess MMPP the Interrupted Poisson Pro cess IPP and the Poisson Pro cess PP Furthermore the input pro cess can b e timeinhomogeneous ie its parameters maychange with time as we shall see in Section An arriving packetcell that nds the token p o ol nonempty departs the system immediately while removing one token from the token p o ol An arriving packetcell that nds the token pool empty joins the queue if the buer is not full Now when the queue is not emptywhich means that the token pool is empty and a token arrives one packetcell departs immediately taking the token with it Arriving cells Departing cells M 321 Buffer 1 2 Token pool L Token generator Figure The leaky bucket rate control scheme Existing mo dels in the op en literature are concerned with steadystate measures Wecan characterize these mo dels as follows uidow mo del for arrival sources are considered in p oint pro cess mo dels with continuoustime in p oint pro cesses It should b e noted here that this denition of the leaky bucket is slightly dierent from the one adopted by ITU and ATM Forum with discretetime in Brownian motion mo dels and analysis based on sample paths in In this pap er we will describ e the continuous timedep endent b ehavior of the leaky bucket adopting a p oint pro cess to characterize cell arrivals Delayed Markov regenerative pro cesses In the development of BMAPG and GIBMAP typ e of queueing mo dels it is commonly assumed that the time origin coincides with a service completion or an arrival instant When studying overload b ehavior of queueing systems as we shall see in this pap er we need mo dels where the time origin do es not necessarily coincide with service completion or arrival instant For this reason in this section we generalize the wellknown Markov regenerative pro cess MRGP to the delayed Markov regenerative pro cess DMRGP and develop the underlying equations that govern the conditional state probabilities Before we formally dene the delayed Markov regenerative pro cess wegive some short of lo ose denition of the Markov regenerative pro cess An MRGP can b e thought of as a pro cess where there exist time ep o chs where the pro cess regenerates in the Markovian sense ie the sto chastic evolution of the marking pro cess do es not dep end on the history of the pro cess but rather on the current state The time ep o chs that the pro cess regenerates together with the value that pro cess has at that p oint form what we call a Markov renewal sequence MRS The sto chastic b ehavior of the Markov regenerative pro cess can b e describ ed bytwo matrices namely Kt global kernel that captures the b ehavior of the pro cess assuming the regeneration has o ccurred and Etlocalkernel that considers the b ehavior b etween two regenerations It has b een shown that matrix V twithentries V t the time dep endent ij state probabilities of an MRGP P Z tj jZ i satises a matrix generalized R t Markov renewal equation V t Et dKxV t x Now for the developmentofthe delayed Markov regenerative pro cess we rst dene the delayed Markov renewal sequence the generalization of the Markov renewal sequence in Markov regenerative theory Denition Asequence of bivariate random variables fY T g is cal led a time homoge n n neous Delayed Markov Renewal Sequence DMRS if T T T Y n n n P fY j T x j Y ig F x ij n P fY j T T x j Y i T Y T Y T g n n n n n n n P fY j T T x j Y ig n n n n P fY j T T x j Y ig K x ij Then the DMRGP is dened
Load more

Recommended publications
  • Designing Traffic Profiles for Bursty Internet Traffic
    Designing Traffic Profiles for Bursty Internet Traffic Xiaowei Yang MIT Laboratory for Computer Science Cambridge, MA 02139 [email protected] Abstract An example of a non-conforming stream is one that has a This paper proposes a new class of traffic profiles that is much higher expected transmission rate than that allowed better suited for metering bursty Internet traffic streams by a traffic profile. than the traditional token bucket profile. A good traffic It is desirable to have a range of traffic profiles for differ- profile should satisfy two criteria: first, it should consider ent classes of traffic, and for differentiation within a class. packets from a conforming traffic stream as in-profile with For example, traffic streams generated by constant bit rate high probability to ensure a strong QoS guarantee; second, video applications have quite different statistics than those it should limit the network resources consumed by a non- generated by web browsing sessions, thus require different conforming traffic stream to no more than that consumed profiles to meet their QoS requirements. It is worth noting by a conforming stream. We model a bursty Internet traffic that the type of traffic we consider in this paper is most of- stream as an ON/OFF stream, where both the ON-period ten generated by document transfers, such as web browsing. and the OFF-period have a heavy-tailed distribution. Our Traditionally, the QoS requirement for such traffic (a.k.a. study shows that the heavy-tailed distribution leads to an elastic traffic) is less obvious than that for the real-time excessive randomness in the long-term session rate distribu- traffic.
    [Show full text]
  • Performance Analysis I
    CS 6323 Complex Networks and Systems: Modeling and Inference Lecture 5: Performance Analysis I Prof. Gregory Provan Department of Computer Science University College Cork Slides: Based on M. Yin (Performability Analysis) Overview •Queuing Models •Birth-Death Process •Poisson Process •Task Graphs Complex Networks and Systems 2 Network Modelling • We model the transmission of packets through a network using Queueing Theory • Enables us to determine several QoS metrics • Throughput times, delays, etc. • Predictive Model • Properties of queueing network depends on • Network topology • Performance for each “path” in network • Network interactions Complex Networks and Systems 3 Queuing Networks • A queuing network consists of service centers and customers (often called jobs) • A service center consists of one or more servers and one or more queues to hold customers waiting for service. : customers arrival rate : service rate 1/24/2014 Complex Networks and Systems 4 Interarrival • Interarrival time: the time between successive customer arrivals • Arrival process: the process that determines the interarrival times • It is common to assume that interarrival times are exponentially distributed random variables. In this case, the arrival process is a Poisson process : customers arrival rate : service rate 0 1 2 n 1/24/2014 Complex Networks and Systems 5 Service Time • The service time depends on how much work the customer needs and how fast the server is able to perform the work • Service times are commonly assumed to be independent, identically distributed (iid) random variables. 1/24/2014 Complex Networks and Systems 6 A Queuing Model Example Server Center 1 Server Center 2 cpu1 Disk1 cpu2 queue Disk2 Arriving customers cpu3 servers Server Center 3 Queuing delay Service time Response time 1/24/2014 Complex Networks and Systems 7 Terminology Term Explanations Buffer size The total number of customers allowed at a service center.
    [Show full text]
  • A Novel Simulation Based Methodology for the Congestion Control in ATM Networks
    A Novel Simulation Based Methodology for the Congestion Control in ATM Networks Heven Patel, Hardik Patel, Aditya Jagannath, Syed Rizvi, Khaled Elleithy Computer Science and Engineering Department University of Bridgeport, Bridgeport, CT Abstract- In this project, we use the OPNET simulation tool client server and source destination networks with various for modeling and analysis of packet data networks. Our project protocol parameters and service categories. We also is mainly focused on the performance analysis of simulate a policing mechanism for ATM networks .In this Asynchronous transfer mode (ATM) networks. Specifically, in section we simulate the performance of the FDDI this project, we simulate two types of high-performance protocol. We consider network throughput, link networks namely, Fiber Distributed Data Interface (FDDI) utilizations, and end-to-end delay by varying network and Asynchronous Transfer Mode (ATM). In the first type of network, we examine the performance of the FDDI protocol by parameters in two network configurations. The leaky varying network parameters in two network configurations. In bucket mechanism limits the difference between the the second type, we build a simple ATM network model and negotiated mean cell rate (MCR) parameter and the actual measure its performance under various ATM service cell rate of a traffic source. It can be viewed as a bucket, categories. Finally, we develop an OPNET process model for placed immediately after each source. Each cell generated leaky bucket congestion control algorithm and examine its by the traffic source carries token and attempts to place it performance and its relative effect on the traffic patterns (loss in the bucket.
    [Show full text]
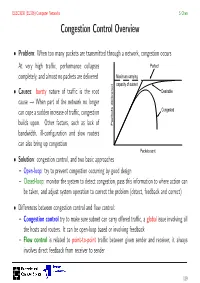
  • Congestion Control Overview
    ELEC3030 (EL336) Computer Networks S Chen Congestion Control Overview • Problem: When too many packets are transmitted through a network, congestion occurs At very high traffic, performance collapses Perfect completely, and almost no packets are delivered Maximum carrying capacity of subnet • Causes: bursty nature of traffic is the root Desirable cause → When part of the network no longer can cope a sudden increase of traffic, congestion Congested builds upon. Other factors, such as lack of Packets delivered bandwidth, ill-configuration and slow routers can also bring up congestion Packets sent • Solution: congestion control, and two basic approaches – Open-loop: try to prevent congestion occurring by good design – Closed-loop: monitor the system to detect congestion, pass this information to where action can be taken, and adjust system operation to correct the problem (detect, feedback and correct) • Differences between congestion control and flow control: – Congestion control try to make sure subnet can carry offered traffic, a global issue involving all the hosts and routers. It can be open-loop based or involving feedback – Flow control is related to point-to-point traffic between given sender and receiver, it always involves direct feedback from receiver to sender 119 ELEC3030 (EL336) Computer Networks S Chen Open-Loop Congestion Control • Prevention: Different policies at various layers can affect congestion, and these are summarised in the table • e.g. retransmission policy at data link layer Transport Retransmission policy • Out-of-order caching
    [Show full text]
  • Markovian Performance Model for Token Bucket Filter with Fixed And
    Markovian Performance Model for Token Bucket Filter with Fixed and Varying Packet Sizes HenrikSchiøler JohnLeth ShibarchiMajumder Abstract—We consider a token bucket mechanism serving a not consider burst arrivals but variable packet lengths and our model heterogeneous flow with a focus on backlog, delay and packet does not suffer from the Markovian approximation found in [6]. loss properties. Previous models have considered the case for We first give algorithmic descriptions of the token bucket filter fixed size packets, i.e. one token per packet with and M/D/1 dynamics for the fixed packet length and variable packet length as- view on queuing behavior. We partition the heterogeneous flow sumptions. The algorithmic descriptions are followed by probabilistic into several packet size classes with individual Poisson arrival modeling sections for the fixed packet length and variable packet intensities. The accompanying queuing model is a full state length cases. Hereafter a section provides the continuous time output model, i.e. buffer content is not reduced to a single quantity but analysis required to obtain precise results for waiting time and packet encompasses the detailed content in terms of packet size classes. loss probabilities. Each theory-section is followed by a results section This yields a high model cardinality for which upper bounds are providing selected numerical results illustrating the virtues of the provided. Analytical results include class specific backlog, delay developed models in terms of available outputs and model flexibility. and loss statistics and are accompanied by results from discrete event simulation. II. TOKEN BUCKET ALGORITHM Keywords— Token bucket filter, performance evaluation, Marko- We assume periodic token replenishment, i.e.
    [Show full text]
  • Quality of Service (Qos) the Internet Was Originally Designed for Best-Effort Service Without Guarantee of Predictable Performance
    rd Data Communication and Networking II 4 class – Department of Network Muayad Najm Abdulla College of IT- University of Babylon Quality of Service (QoS) The Internet was originally designed for best-effort service without guarantee of predictable performance. Best-effort service is often sufficient for a traffic that is not sensitive to delay, such as file transfers and e-mail. Such a traffic is called elastic because it can stretch to work under delay conditions; it is also called available bit rate because applications can speed up or slow down according to the available bit rate. The real-time traffic generated by some multimedia applications is delay sensitive and therefore requires guaranteed and predictable performance. Quality of service (QoS) is an internetworking issue that refers to a set of techniques and mechanisms that guarantee the performance of the network to deliver predictable service to an application program. DATA-FLOW CHARACTERISTICS Traditionally, four types of characteristics are attributed to a flow: reliability, delay, jitter, and bandwidth. To provide quality of server (QoS). Reliability Reliability is a characteristic that a flow needs in order to deliver the packets safe and sound to the destination. Lack of reliability means losing a packet or acknowledgment, which entails retransmission. However, the sensitivity of different application programs to reliability varies. For example, reliable transmission is more important for electronic mail, file transfer, and Internet access than for telephony or audio conferencing. Delay Source-to-destination delay is another flow characteristic. Again, applications can tolerate delay in different degrees. In this case, telephony, audio conferencing, video conferencing, and remote logging need minimum delay, while delay in file transfer or e-mail is less important.
    [Show full text]
  • Computer Networks Prof
    CMSC417 Computer Networks Prof. Ashok K. Agrawala © 2017 Ashok Agrawala September 27, 2018 Fall 2018 CMSC417 1 Message, Segment, Packet, and Frame Fall 2018 CMSC417 2 Quality of Service • Application requirements • Traffic shaping • Packet scheduling • Admission control • Integrated services • Differentiated services September 18 CMSC417 Set 6 3 Application Requirements (1) Different applications care about different properties • We want all applications to get what they need . “High” means a demanding requirement, e.g., low delay CMSC417 Set 6 Application Requirements (2) Network provides service with different kinds of QoS (Quality of Service) to meet application requirements Network Service Application Constant bit rate Telephony Real-time variable bit rate Videoconferencing Non-real-time variable bit rate Streaming a movie Available bit rate File transfer Example of QoS categories from ATM networks CMSC417 Set 6 Categories of QoS and Examples 1.Constant bit rate • Telephony 2.Real-time variable bit rate • Compressed videoconferencing 3.Non-real-time variable bit rate • Watching a movie on demand 4.Available bit rate • File transfer September 18 CMSC417 Set 6 6 Buffering Smoothing the output stream by buffering packets. September 18 CMSC417 Set 6 7 Traffic Shaping (1) Traffic shaping regulates the average rate and burstiness of data Shape traffic entering the network here • Lets us make guarantees CMSC417 Set 6 Traffic Shaping (2) Token/Leaky bucket limits both the average rate (R) and short-term burst (B) of traffic • For token, bucket size is B, water enters at rate R and is removed to send; opposite for leaky. to send to send Leaky bucket Token bucket (need not full to send) (need some water to send) CMSC417 Set 6 The Leaky Bucket Algorithm (a) A leaky bucket with water.
    [Show full text]
  • Modeling Traffic Shaping and Traffic Policing in Packet-Switched Networks
    Journal of Computer Sciences and Applications, 2018, Vol. 6, No. 2, 75-81 Available online at http://pubs.sciepub.com/jcsa/6/2/4 ©Science and Education Publishing DOI:10.12691/jcsa-6-2-4 Modeling Traffic Shaping and Traffic Policing in Packet-Switched Networks Wlodek M. Zuberek 1,* , Dariusz Strzeciwilk 2 1Department of Computer Science, Memorial University, St. John’s, Canada 2Department of Applied Informatics, University of Life Sciences, Warsaw, Poland *Corresponding author: [email protected] Received August 26, 2018; Revised October 01, 2018; Accepted October 26, 2018 Abstract Traffic shaping is a computer network traffic management technique which delays some packets to make the traffic compliant with the desired traffic profile. Traffic policing is the process of monitoring network traffic for compliance with a traffic contract and dropping the excess traffic. Both traffic shaping and policing use two popular methods, known as leaky bucket and token bucket. The paper proposes timed Petri net models of both methods and uses these models to show the effects of traffic shaping and policing on the performance of very simple networks. Keywords : traffic shaping, traffic policing, packet-switched networks, leaky bucket algorithm, token bucket algorithm, timed Petri nets, performance analysis Cite This Article: Wlodek M. Zuberek, and Dariusz Strzeciwilk, “Modeling Traffic Shaping and Traffic Policing in Packet-Switched Networks.” Journal of Computer Sciences and Applications , vol. 6, no. 2 (2018): 75-81. doi: 10.12691/jcsa-6-2-4. If, in this model, the exponentially distributed inter-arrival times are replaced by deterministic arrivals (i.e., the model 1. Introduction becomes D/M/1), the average waiting time is: ! Traffic shaping is a computer network traffic management Tw " technique which delays some packets to make the traffic 2s (1# ! ) compliant with the desired traffic profile [1] .
    [Show full text]
  • L2: Congestion Control G When One Part of the Subnet (E.G
    L2: Congestion Control g When one part of the subnet (e.g. one or more routers in an area) becomes overloaded, congestion results. g Because routers are receiving packets faster than they can forward them, one of two things must happen: – The subnet must prevent additional packets from entering the congested region until those already present can be processed. – The congested routers can discard queued packets to make room for those that are arriving. g http://www.cisco.com/en/US/products/ps6558/products_ios_technology_home.html g http://www.cisco.com/en/US/netsol/ns577/networking_solutions_white_paper09186a00801eb831.shtml g http://www.cisco.com/univercd/cc/td/doc/cisintwk/ito_doc/qos.htm 1 Traffic conditioner g A traffic stream is selected by a classifier, which steers the packets to a logical instance of a traffic conditioner. g A meter is used (where appropriate) to measure the traffic stream against a traffic profile. g The state of the meter with respect to a particular packet (e.g., whether it is in- or out-of-profile) may be used to affect a marking, dropping, or shaping action. 2 Factors that Cause Congestion g Packet arrival rate exceeds the outgoing link capacity. g Insufficient memory to store arriving packets g Bursty traffic g Slow processor 3 Congestion Control vs Flow Control g Congestion control is a global issue – involves every router and host within the subnet g Flow control – scope is point-to-point; involves just sender and receiver. 4 Traffic Shaping g Another method of congestion control is to “shape” the traffic before it enters the network.
    [Show full text]
  • Internet Technology 13
    Internet Technology 13. Network Quality of Service Paul Krzyzanowski Rutgers University Spring 2016 April 22, 2016 352 © 2013-2016 Paul Krzyzanowski 1 Internet gives us “best effort” • The Internet was designed to provide best effort delivery – No guarantees on when or if packet will get delivered • Software tries to make up for this – Buffering, sequence numbers, retransmission, timestamps • Can we enhance the network to support multimedia needs? – Control quality of service (QoS) with resource allocation & prioritization on the network April 22, 2016 352 © 2013-2016 Paul Krzyzanowski 2 What factors make up QoS? • Bandwidth (bit rate) – Average number of bits per second through the network • Delay (latency) – Average time for data to get from one endpoint to its destination • Jitter – Variation in end-to-end delay • Loss (packet errors and dropped packets) – Percentage of packets that don’t reach their destination April 22, 2016 352 © 2013-2016 Paul Krzyzanowski 3 Service Models for QoS • No QoS (best effort) – Default behavior for IP with no QoS – No preferential treatment – Host is not involved in specifying service quality needs • Soft QoS (Differentiated Services) – No explicit setup – Identify one type of service (data flow) vs. another – Certain classes get preferential treatment over others • Hard QoS (Integrated Services) – Network makes commitment to deliver the required quality of service – Host makes an end-to-end reservation • Traffic flows are reserved April 22, 2016 352 © 2013-2016 Paul Krzyzanowski 4 Link scheduling at
    [Show full text]
  • Traffic Shaping, Traffic Policing
    Traffic Shaping, Traffic Policing Peter Puschner, Institut für Technische Informatik Traffic Shaping, Traffic Policing • Enforce compliance of traffic to a given traffic profile (e.g., rate limiting) • By delaying or dropping certain packets, one can (i) optimize or guarantee performance, (ii) improve latency, and/or (iii) increase or guarantee bandwidth for other packets • Traffic shaping: delays non-conforming traffic • Traffic policing: drops or marks non-conforming traffic Peter Puschner, TU Wien 2 Traffic Shaping • Traffic metering to check compliance of packets with traffic contract e.g., leaky bucket / token bucket algorithm • Imposes limits on bandwidth and burstiness • Buffering of packets that arrive early – Buffer dimensioning (?) • Strategy to deal with full buffer – Tail drop (à policing) – Random Early Discard – Unshaped forwarding of overflow traffic Peter Puschner, TU Wien 3 Traffic Shaping • Self limiting sources • Shaping by network switches • Shaping traffic uniformly by rate • More sophisticated characteristics (allow for defined variability in traffic) Peter Puschner, TU Wien 4 Token Bucket Algorithm • Bucket capacity: C [tokens] • Token arrival rate: r [tokens per second] • When a packet of n bytes arrives, n tokens are removed from the bucket and the packet is sent • If fewer than n tokens available, no token is removed and the packet is considered to be non-conformant Peter Puschner, TU Wien 5 Leaky Bucket Algorithm n n n C C r … leak rate Peter Puschner, TU Wien 6 Leaky Bucket Algorithm n • Bucketn with capacity C leaks at fixedn rate r • TheC bucket must never overflow C • If the bucket is empty it stops leaking • A packet is conformant, if the amount of water, n, can be added to the bucketr … leak without rate causing an overflow; n is either constant or proportional to packet size • For non-conformant packets, no water is added to the bucket Peter Puschner, TU Wien 7 Leaky Bucket Properties Best average rate (over infinite time) r [bytes/s] r /n [messages/s], with message size n bytes Maximum burst size assume max.
    [Show full text]
  • Distributed Policing with Full Utilization and Rate Guarantees
    Distributed Policing with Full Utilization and Rate Guarantees by Albert C. B. Choi A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics in Computer Science Waterloo, Ontario, Canada, 2009 c Albert C. B. Choi 2009 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract A network service provider typically sells service at a fixed traffic rate to cus- tomers. This rate is enforced by allowing or dropping packets that pass through, in a process called policing. Distributed policing is a version of the problem where a number of policers must limit their combined traffic allowance to the specified rate. The policers must coordinate their behaviour such that customers are fully allowed the rate they pay for, without receiving too much more, while maintaining some semblance of fairness between packets arriving at one policer versus another. A review of prior solutions shows that most use predictions or estimations to heuristically allocate rates, and thus cannot provide any error bounds or guarantees on the achieved rate under all scenarios. Other solutions may suffer from starvation or unfairness under certain traffic demand patterns. We present a new global \leaky bucket" approach that provably prevents star- vation, guarantees full utilization, and provides a simple upper bound on the rate allowed under any incoming traffic pattern. We find that the algorithm guarantees a minimum 1=n share of the rate for each policer, and achieves close to max-min fairness in many, but not all cases.
    [Show full text]