Forming a Regular Pentagon, Decagon and Pentagram Using Origami Technique
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 and 1991 Bradley C. Klypchak a Dissertation Submitted to the Graduate
PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 AND 1991 Bradley C. Klypchak A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2007 Committee: Dr. Jeffrey A. Brown, Advisor Dr. John Makay Graduate Faculty Representative Dr. Ron E. Shields Dr. Don McQuarie © 2007 Bradley C. Klypchak All Rights Reserved iii ABSTRACT Dr. Jeffrey A. Brown, Advisor Between 1984 and 1991, heavy metal became one of the most publicly popular and commercially successful rock music subgenres. The focus of this dissertation is to explore the following research questions: How did the subculture of heavy metal music between 1984 and 1991 evolve and what meanings can be derived from this ongoing process? How did the contextual circumstances surrounding heavy metal music during this period impact the performative choices exhibited by artists, and from a position of retrospection, what lasting significance does this particular era of heavy metal merit today? A textual analysis of metal- related materials fostered the development of themes relating to the selective choices made and performances enacted by metal artists. These themes were then considered in terms of gender, sexuality, race, and age constructions as well as the ongoing negotiations of the metal artist within multiple performative realms. Occurring at the juncture of art and commerce, heavy metal music is a purposeful construction. Metal musicians made performative choices for serving particular aims, be it fame, wealth, or art. These same individuals worked within a greater system of influence. Metal bands were the contracted employees of record labels whose own corporate aims needed to be recognized. -

How Can You Put Shapes Together to Make Other Shapes?
Lesson 27 Understand Tiling in Rectangles Name: How can you put shapes together to make other shapes? Study the example showing how to put shapes together to make other shapes. Then solve Problems 1–4. Example How can you use smaller shapes to make a circle? Look at the shapes in the green box Draw lines to show how you could use the shapes Write how many of each shape you would need 2 4 1 Draw a line to show how you could use squares like the one in the green box to make a rectangle How many squares would you need? squares 2 Draw lines to show how you could use triangles like the one in the green box to make a rectangle How many triangles would you need? triangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Understand Tiling in Rectangles 283 Solve. 3 Draw lines to show how you could use hexagons to make the first shape below Then show how you could use trapezoids to make the second shape How many of each shape would you need? hexagons trapezoids 4 Draw lines to show how you could use triangles to make the first shape below Then show how you could use trapezoids to make the second shape Then show how you could use rhombuses to make the third shape How many of each shape would you need? triangles trapezoids rhombuses 284 Lesson 27 Understand Tiling in Rectangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Name: Draw and Count Squares Study the example showing how to draw and count squares. -

Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface. -
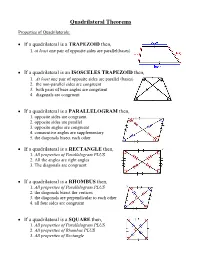
Quadrilateral Theorems
Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3. -

Applying the Polygon Angle
POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°. -

Polygon Review and Puzzlers in the Above, Those Are Names to the Polygons: Fill in the Blank Parts. Names: Number of Sides
Polygon review and puzzlers ÆReview to the classification of polygons: Is it a Polygon? Polygons are 2-dimensional shapes. They are made of straight lines, and the shape is "closed" (all the lines connect up). Polygon Not a Polygon Not a Polygon (straight sides) (has a curve) (open, not closed) Regular polygons have equal length sides and equal interior angles. Polygons are named according to their number of sides. Name of Degree of Degree of triangle total angles regular angles Triangle 180 60 In the above, those are names to the polygons: Quadrilateral 360 90 fill in the blank parts. Pentagon Hexagon Heptagon 900 129 Names: number of sides: Octagon Nonagon hendecagon, 11 dodecagon, _____________ Decagon 1440 144 tetradecagon, 13 hexadecagon, 15 Do you see a pattern in the calculation of the heptadecagon, _____________ total degree of angles of the polygon? octadecagon, _____________ --- (n -2) x 180° enneadecagon, _____________ icosagon 20 pentadecagon, _____________ These summation of angles rules, also apply to the irregular polygons, try it out yourself !!! A point where two or more straight lines meet. Corner. Example: a corner of a polygon (2D) or of a polyhedron (3D) as shown. The plural of vertex is "vertices” Test them out yourself, by drawing diagonals on the polygons. Here are some fun polygon riddles; could you come up with the answer? Geometry polygon riddles I: My first is in shape and also in space; My second is in line and also in place; My third is in point and also in line; My fourth in operation but not in sign; My fifth is in angle but not in degree; My sixth is in glide but not symmetry; Geometry polygon riddles II: I am a polygon all my angles have the same measure all my five sides have the same measure, what general shape am I? Geometry polygon riddles III: I am a polygon. -

Properties of N-Sided Regular Polygons
PROPERTIES OF N-SIDED REGULAR POLYGONS When students are first exposed to regular polygons in middle school, they learn their properties by looking at individual examples such as the equilateral triangles(n=3), squares(n=4), and hexagons(n=6). A generalization is usually not given, although it would be straight forward to do so with just a min imum of trigonometry and algebra. It also would help students by showing how one obtains generalization in mathematics. We show here how to carry out such a generalization for regular polynomials of side length s. Our starting point is the following schematic of an n sided polygon- We see from the figure that any regular n sided polygon can be constructed by looking at n isosceles triangles whose base angles are θ=(1-2/n)(π/2) since the vertex angle of the triangle is just ψ=2π/n, when expressed in radians. The area of the grey triangle in the above figure is- 2 2 ATr=sh/2=(s/2) tan(θ)=(s/2) tan[(1-2/n)(π/2)] so that the total area of any n sided regular convex polygon will be nATr, , with s again being the side-length. With this generalized form we can construct the following table for some of the better known regular polygons- Name Number of Base Angle, Non-Dimensional 2 sides, n θ=(π/2)(1-2/n) Area, 4nATr/s =tan(θ) Triangle 3 π/6=30º 1/sqrt(3) Square 4 π/4=45º 1 Pentagon 5 3π/10=54º sqrt(15+20φ) Hexagon 6 π/3=60º sqrt(3) Octagon 8 3π/8=67.5º 1+sqrt(2) Decagon 10 2π/5=72º 10sqrt(3+4φ) Dodecagon 12 5π/12=75º 144[2+sqrt(3)] Icosagon 20 9π/20=81º 20[2φ+sqrt(3+4φ)] Here φ=[1+sqrt(5)]/2=1.618033989… is the well known Golden Ratio. -

Interior and Exterior Angles of Polygons 2A
Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org G.CO.C.11: Interior and Exterior Angles of Polygons 2a 1 Which type of figure is shown in the accompanying 5 In the diagram below of regular pentagon ABCDE, diagram? EB is drawn. 1) hexagon 2) octagon 3) pentagon 4) quadrilateral What is the measure of ∠AEB? 2 What is the measure of each interior angle of a 1) 36º regular hexagon? 2) 54º 1) 60° 3) 72º 2) 120° 4) 108º 3) 135° 4) 270° 6 What is the measure, in degrees, of each exterior angle of a regular hexagon? 3 Determine, in degrees, the measure of each interior 1) 45 angle of a regular octagon. 2) 60 3) 120 4) 135 4 Determine and state the measure, in degrees, of an interior angle of a regular decagon. 7 A stop sign in the shape of a regular octagon is resting on a brick wall, as shown in the accompanying diagram. What is the measure of angle x? 1) 45° 2) 60° 3) 120° 4) 135° 1 Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org 8 One piece of the birdhouse that Natalie is building 12 The measure of an interior angle of a regular is shaped like a regular pentagon, as shown in the polygon is 120°. How many sides does the polygon accompanying diagram. have? 1) 5 2) 6 3) 3 4) 4 13 Melissa is walking around the outside of a building that is in the shape of a regular polygon. -

Formulas Involving Polygons - Lesson 7-3
you are here > Class Notes – Chapter 7 – Lesson 7-3 Formulas Involving Polygons - Lesson 7-3 Here’s today’s warmup…don’t forget to “phone home!” B Given: BD bisects ∠PBQ PD ⊥ PB QD ⊥ QB M Prove: BD is ⊥ bis. of PQ P Q D Statements Reasons Honors Geometry Notes Today, we started by learning how polygons are classified by their number of sides...you should already know a lot of these - just make sure to memorize the ones you don't know!! Sides Name 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon 8 Octagon 9 Nonagon 10 Decagon 11 Undecagon 12 Dodecagon 13 Tridecagon 14 Tetradecagon 15 Pentadecagon 16 Hexadecagon 17 Heptadecagon 18 Octadecagon 19 Enneadecagon 20 Icosagon n n-gon Baroody Page 2 of 6 Honors Geometry Notes Next, let’s look at the diagonals of polygons with different numbers of sides. By drawing as many diagonals as we could from one diagonal, you should be able to see a pattern...we can make n-2 triangles in a n-sided polygon. Given this information and the fact that the sum of the interior angles of a polygon is 180°, we can come up with a theorem that helps us to figure out the sum of the measures of the interior angles of any n-sided polygon! Baroody Page 3 of 6 Honors Geometry Notes Next, let’s look at exterior angles in a polygon. First, consider the exterior angles of a pentagon as shown below: Note that the sum of the exterior angles is 360°. -

Geometric Constructions of Regular Polygons and Applications to Trigonometry Introduction
Geometric Constructions of Regular Polygons and Applications to Trigonometry José Gilvan de Oliveira, Moacir Rosado Filho, Domingos Sávio Valério Silva Abstract: In this paper, constructions of regular pentagon and decagon, and the calculation of the main trigonometric ratios of the corresponding central angles are approached. In this way, for didactic purposes, it is intended to show the reader that it is possible to broaden the study of Trigonometry by addressing new applications and exercises, for example, with angles 18°, 36° and 72°. It is also considered constructions of other regular polygons and a relation to a construction of the regular icosahedron. Introduction The main objective of this paper is to approach regular pentagon and decagon constructions, together with the calculation of the main trigonometric ratios of the corresponding central angles. In textbooks, examples and exercises involving trigonometric ratios are usually restricted to so-called notable arcs of angles 30°, 45° and 60°. Although these angles are not the main purpose of this article, they will be addressed because the ingredients used in these cases are exactly the same as those we will use to build the regular pentagon and decagon. The difference to the construction of these last two is restricted only to the number of steps required throughout the construction process. By doing so, we intend to show the reader that it is possible to broaden the study of Trigonometry by addressing new applications and exercises, for example, with angles 18°, 36° and 72°. The ingredients used in the text are those found in Plane Geometry and are very few, restricted to intersections of lines and circumferences, properties of triangles, and Pythagorean Theorem. -

Petrie Schemes
Canad. J. Math. Vol. 57 (4), 2005 pp. 844–870 Petrie Schemes Gordon Williams Abstract. Petrie polygons, especially as they arise in the study of regular polytopes and Coxeter groups, have been studied by geometers and group theorists since the early part of the twentieth century. An open question is the determination of which polyhedra possess Petrie polygons that are simple closed curves. The current work explores combinatorial structures in abstract polytopes, called Petrie schemes, that generalize the notion of a Petrie polygon. It is established that all of the regular convex polytopes and honeycombs in Euclidean spaces, as well as all of the Grunbaum–Dress¨ polyhedra, pos- sess Petrie schemes that are not self-intersecting and thus have Petrie polygons that are simple closed curves. Partial results are obtained for several other classes of less symmetric polytopes. 1 Introduction Historically, polyhedra have been conceived of either as closed surfaces (usually topo- logical spheres) made up of planar polygons joined edge to edge or as solids enclosed by such a surface. In recent times, mathematicians have considered polyhedra to be convex polytopes, simplicial spheres, or combinatorial structures such as abstract polytopes or incidence complexes. A Petrie polygon of a polyhedron is a sequence of edges of the polyhedron where any two consecutive elements of the sequence have a vertex and face in common, but no three consecutive edges share a commonface. For the regular polyhedra, the Petrie polygons form the equatorial skew polygons. Petrie polygons may be defined analogously for polytopes as well. Petrie polygons have been very useful in the study of polyhedra and polytopes, especially regular polytopes. -

Quadrilaterals
Name: Quadrilaterals Match the quadrilateral with its definition. a. 1. All sides are the same length. There are four right angles. Parallelogram b. 2. There is only one pair of parallel sides. Rectangle c. 3. Opposite sides are parallel and the same length. There are four right angles. Trapezoid d. 4. There are two pairs of parallel sides. All sides are the same length. Rhombus 5. There are two pairs of opposite parallel e. sides. Square 6. List two ways a rectangle and square are alike and one way in which they are different. Super Teacher Worksheets - www.superteacherworksheets.com ANSWER KEY Quadrilaterals Match the quadrilateral with its definition. a. e 1. All sides are the same length. There are four right angles. Parallelogram b. c 2. There is only one pair of parallel sides. Rectangle c. b 3. Opposite sides are parallel and the same length. There are four right angles. Trapezoid d. d 4. There are two pairs of parallel sides. All sides are the same length. Rhombus a 5. There are two pairs of opposite parallel e. sides. Square 6. List two ways a rectangle and square are alike and one way in which they are different. Rectangles and squares are alike in that both have two pairs of parallel sides and four right angles. They are different because a square must have four equal sides lengths and a rectangle has two pairs of equal side lengths. Super Teacher Worksheets - www.superteacherworksheets.com.