DOCSLIB.ORG

Constraining the Properties of Milky Way Dwarf Spheroidals with Surface Brightness & Velocity Dispersion Data Introduction Justin Craig, Casey R

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Constraining the Properties of Milky Way Dwarf Spheroidals with Surface Brightness & Velocity Dispersion Data Introduction Justin Craig, Casey R Constraining the Properties of Milky Way Dwarf Spheroidals with Surface Brightness & Velocity Dispersion Data Introduction Justin Craig, Casey R. Watson Department of Physics & Astronomy, Millikin University, Decatur, IL, USA. Dark matter (DM) is the dominant form of matter in the universe [1]. Observations of Results Table 1. The star-related quantities derived from observations and steps I and II with the values for 푛, 훾, and 푅푒 from Ref. [7] and 푦푒 = 푅푒/푅∗. rotation curves (Fig. 1), suggest that every galaxy is embedded within a large DM halo (Fig. (B) (NFW) Abstract Galaxy 풏 휸 풚풆 푹풆/(pc) 푹∗/(pc) 휶 (B) 휶 (NFW) 휷ퟎ 휷ퟎ 휷∞ (B) 휷∞ (NFW) 푫 (B) 푫 (NFW) 2), that comprises, on average, 84% of the mass of each galaxy and the same fraction of CVI 5 0.60+0.08 0.785+0.050 452 ± 13 576 ± 17 1.0 ± 0.1 0.7 ± 0.1 0.27 ± 0.05 0.97 ± 0.01 -1.51 ± 0.57 -12.15 ± 0.01 7.7 ± 2.2 3.6 ± 1.2 Using a combination of surface brightness and velocity dispersion data, we simultaneously −0.06 −0.032 matter in the universe as a whole [1,2,3]. CVII 5 0.53+0.12 0.756+0.024 70.7 ± 11.2 93.6 ± 14.8 1.1 ± 0.1 0.9 ± 0.1 0.29 ± 0.05 0.93 ± 0.02 0.23 ± 0.20 −7.90 ± 1.16 3.5 ± 1.5 1.6 ± 0.7 constrain the velocity anisotropy and dark matter mass profiles of Milky Way dwarf spheroidals −0.10 −0.031 +0.02 +0.001 (dSphs). Our findings indicate strong correlations between the distributions of visible and dark Draco 9 0.27−0.01 0.559−0.003 214 ± 2 383 ± 4 1.0 ± 0.1 0.7 ± 0.1 0.11 ± 0.05 0.75 ± 0.02 -0.83 ± 0.29 −3.89 ± 0.67 8.3 ± 2.5 5.0 ± 1.0 +0.01 +0.002 matter within the dSphs and provide further insights into the cusp vs. core debate. Fornax 9 0.27−0.01 0.504−0.002 838 ± 3 1662 ± 6 1.0 ± 0.1 0.7 ± 0.1 0.11 ± 0.05 0.75 ± 0.02 0.92 ± 0.23 −3.76 ± 0.45 11.1 ± 1.1 5.9 ± 1.3 +0.01 +0.002 Leo I 9 0.20−0.01 0.456−0.001 270 ± 2 592 ± 4 1.2 ± 0.1 1.8 ± 0.3 0.17 ± 0.04 0.94 ± 0.05 -1.52 ± 0.35 −16.42 ± 2.76 8.0 ± 1.2 3.1 ± 0.5 +0.03 +0.002 Leo II 9 0.48−0,03 0.368−0.003 171 ± 2 465 ± 5 1.5 ± 0.1 0.7 ± 0.1 0.43 ± 0.04 0.87 ± 0.02 -1.30 ± 0.18 -5.49 ± 0.73 7.4 ± 1.3 4.5 ± 1.2 II. Spherical Jeans Equation Analysis +0.01 +0.002 Ret2 9 0.11−0.01 0.544−0.002 55 ± 5 101 ± 9 1.0 ± 0.1 0.7 ± 0.1 0.03 ± 0.05 0.72 ± 0.02 -1.63 ± 0.40 −9.32 ± 1.30 3.1 ± 0.2 1.5 ± 0.2 Given 푅 and Eqn. (2), we can now use the Spherical Jeans Equation (SJE: Eqn. 4) to determine other +0.05 +0.017 ∗ Sextans 5 0.81−0.05 0.553−0.018 413 ± 3 747 ± 5 1.1 ± 0.1 0.7 ± 0.1 0.43 ± 0.04 1.00 ± 0.01 -0.08 ± 0.02 −3.42 ± 1.64 7.6 ± 2.1 4.7 ± 1.5 parameters of interest [18] +0.02 +0.004 U Minor 5 0.27−0.01 0.863−0.007 407 ± 2 472 ± 2 1.0 ± 0.1 0.9 ± 0.1 0.11 ± 0.05 0.06 ± 0.05 −0.11 ± 0.19 0.02 ± 0.13 9.6 ± 1.9 9.9 ± 1.9 푑푙푛휎2(푦) 푑푙푛휈(푦) Fig. 1: Rotation curves reveal the need for extra, unseen mass in galaxies [4]. Fig. 2: DM Halo [5] 푦휎2(푦) 푟 + + 2훽(푦) = −휎2퐼(푥) . (4) 푟 푑푙푛푟 푑푙푛푟 0 Table 2. The DM quantities derived in step III for both the Burkert profile (B) and the NFW profile. In column 8, 9 and 10, we show the mass at 푅 (푀 ) found from an equation derived in Ref. [14] (denoted as W09), the Burkert profile (B), and the NFW profile. The final three As the most DM-dominated systems in the universe, dwarf galaxies serve as excellent DM 2 푒 푒 We adopt the following forms of the radial velocity dispersion profile and velocity anisotropy profile, 휎푟 (푦) columns show the error in our models relative to the data (SD푟푒푙) for the Burkert (B) and NFW profiles and the ratio of NFW/B uncertainties. laboratories [1,2]. In this poster, we use stellar velocity dispersion and surface brightness and 훽(푦), respectively, for our analysis: 푴ퟎ/ 푴ퟎ/ 푴풆/ 푴풆/ 푴풆/ 퐒퐃 퐒퐃 퐒퐃풓풆풍 (퐍퐅퐖) profile data to infer the DM properties of 9 Milky Way dwarf spheroidal galaxies (dSphs). 푠 2 (푡−푠)/2 Galaxy 풓 /(pc) 풓 /(pc) 흆 /(푴 풑풄−ퟑ) 흆 /(푴 풑풄−ퟑ) (ퟏ풆ퟖ푴 ) (ퟏ풆ퟖ푴 ) (ퟏ풆ퟕ푴 ) (ퟏ풆ퟕ푴 ) (ퟏ풆ퟕ푴 ) 풓풆풍 풓풆풍 휎 푦 = 퐷푦 (1 + 푦 ) , (5) 풐 풔 ퟎ ⊙ 풔 ⊙ ⊙ ⊙ ⊙ ⊙ ⊙ (B) (NFW) 퐒퐃 (퐁) 푟 (B) (NFW) (W09) (B) (NFW) 풓풆풍 Data and Galaxy Selection where D is a normalization constant, and t and s are free parameters, and CVI 576 ± 52 883 ± 103 0.087 ± 0.019 0.037 ± 0.008 2.09 ± 1.02 2.62 ± 1.49 1.68 1.61 ± 0.79 2.18 ± 1.24 1.133 1.354 1.195 CVII 85.1 ± 8.5 104 ± 13 0.464 ± 0.035 0.315 ± 0.060 0.04 ± 0.02 0.04 ± 0.03 0.04 0.03 ± 0.02 0.05 ± 0.03 0.645 0.663 1.028 In this work, we only consider Milky Way (MW) dSphs for which both high quality surface 훽 +훽 푦2 훽 푦 = 표 ∞ , (6) Draco 383 ± 35 547 ± 68 0.307 ± 0.044 0.095 ± 0.026 2.17 ± 0.74 1.97 ± 0.90 0.79 0.76 ± 0.26 0.96 ± 0.44 0.856 0.970 1.134 brightness (SB) and velocity dispersion data exist. We make further cuts based on 3 1+푦2 additional factors: 1. Tidal disruption, 2. Spherical Symmetry, and 3. Constraints on the Fornax 1662 ± 151 2374 ± 297 0.020 ± 0.003 0.007 ± 0.002 11.35 ± 3.00 11.51 ± 5.58 4.11 3.09 ± 0.82 4.76 ± 2.18 0.523 1.149 2.198 inner slope, g, of the stellar density profile, 휈 푟 . where 훽표 and 훽∞ are free parameters that describe b at the center of a dSph and at large radii, respectively Leo I 493 ± 38 328 ± 66 0.180 ± 0.020 0.227 ± 0.062 2.71 ± 0.76 1.01 ± 0.51 1.23 0.91 ± 0.26 1.50 ± 0.76 0.770 0.890 1.155 2 2 [16].The coefficient 휎 in Eqn. (4) is given by 휎 = 퐺푀 Τ푅 , where 푀 = 4휋휌 푟 3 , 휌 and 푟 are, Leo II 310 ± 19 664 ± 83 0.358 ± 0.014 0.063 ± 0.016 1.34 ± 0.38 2.31 ± 1.15 0.65 0.46 ± 0.13 0.56 ± 0.28 0.806 1.129 1.401 1. Tidal disruption 0 0 0 ∗ 0 퐷푀 퐷푀 퐷푀 퐷푀 respectively, the density and scale radius parameters of the chosen DM halo model, and 푥 = 푟Τ푟 . The two Ret2 101 ± 9 144 ± 18 0.683 ± 0.095 0.214 ± 0.058 0.09 ± 0.02 0.08 ± 0.03 0.04 0.03 ± 0.01 0.04 ± 0.01 0.114 0.231 2.035 MW dSphs are often tidally disrupted by the gravitational influence of the much larger MW 퐷푀 DM density models we consider are the Burkert (푟 = 푟 ; [19]) and NFW (푟 = 푟 ; [20]) profiles, and the Sextans 679 ± 57 1068 ± 133 0.037 ± 0.004 0.016 ± 0.002 1.45 ± 0.62 2.38 ± 1.22 0.89 0.62 ± 0.27 1.14 ± 0.59 0.972 1.115 1.147 that they orbit, e.g., [6]. Tidal disruption disturbs the equilibrium that is assumed in the 퐷푀 표 퐷푀 푠 mass integrals over these profiles (퐼(푥) in Eqn. (4)) are shown in Eqns. (7) and (8). U Minor 471 ± 43 524 ± 52 0.135 ± 0.025 0.114 ± 0.020 1.78 ± 0.67 2.07 ± 0.77 2.22 1.67 ± 0.63 1.55 ± 0.58 0.992 0.973 0.980 orbital analysis we will conduct, so we must discard dSphs undergoing disruption. 2 ∞ 푥 푑푥 푟 (7) 2000 2000 = Spherical Symmetry 퐼퐵푢푟푘푒푟푡 푥 = ׬ 2 , 푥 .2 0 (1+푥)(1+푥 ) 푟0 1750 1750 Due to increased and uncertain projection effects, analysis of velocity dispersion data is 1500 1500 ∞ 푥2푑푥 푟 skewed for dSphs that are more ellipsoidal. We therefore restrict our galaxy sample to 1250 1250 (퐼푁퐹푊 푥 = ׬ 2 , 푥 = (8 0 푥(1+푥) 푟푠 (pc) dSphs that are statistically well-described by only 1 axial radius (spherical) rather than 3 (pc) 1000 1000 s 0 r = 1.72R r r r = 2.40R independent axial radii (ellipsoidal), according to the analysis of Ref.
Load more

Recommended publications
  • Central Coast Astronomy Virtual Star Party May 15Th 7Pm Pacific
    Central Coast Astronomy Virtual Star Party May 15th 7pm Pacific Welcome to our Virtual Star Gazing session! We’ll be focusing on objects you can see with binoculars or a small telescope, so after our session, you can simply walk outside, look up, and understand what you’re looking at. CCAS President Aurora Lipper and astronomer Kent Wallace will bring you a virtual “tour of the night sky” where you can discover, learn, and ask questions as we go along! All you need is an internet connection. You can use an iPad, laptop, computer or cell phone. When 7pm on Saturday night rolls around, click the link on our website to join our class. CentralCoastAstronomy.org/stargaze Before our session starts: Step 1: Download your free map of the night sky: SkyMaps.com They have it available for Northern and Southern hemispheres. Step 2: Print out this document and use it to take notes during our time on Saturday. This document highlights the objects we will focus on in our session together. Celestial Objects: Moon: The moon 4 days after new, which is excellent for star gazing! *Image credit: all astrophotography images are courtesy of NASA & ESO unless otherwise noted. All planetarium images are courtesy of Stellarium. Central Coast Astronomy CentralCoastAstronomy.org Page 1 Main Focus for the Session: 1. Canes Venatici (The Hunting Dogs) 2. Boötes (the Herdsman) 3. Coma Berenices (Hair of Berenice) 4. Virgo (the Virgin) Central Coast Astronomy CentralCoastAstronomy.org Page 2 Canes Venatici (the Hunting Dogs) Canes Venatici, The Hunting Dogs, a modern constellation created by Polish astronomer Johannes Hevelius in 1687.
    [Show full text]
  • What Is an Ultra-Faint Galaxy?
    What is an ultra-faint Galaxy? UCSB KITP Feb 16 2012 Beth Willman (Haverford College) ~ 1/10 Milky Way luminosity Large Magellanic Cloud, MV = -18 image credit: Yuri Beletsky (ESO) and APOD NGC 205, MV = -16.4 ~ 1/40 Milky Way luminosity image credit: www.noao.edu Image credit: David W. Hogg, Michael R. Blanton, and the Sloan Digital Sky Survey Collaboration ~ 1/300 Milky Way luminosity MV = -14.2 Image credit: David W. Hogg, Michael R. Blanton, and the Sloan Digital Sky Survey Collaboration ~ 1/2700 Milky Way luminosity MV = -11.9 Image credit: David W. Hogg, Michael R. Blanton, and the Sloan Digital Sky Survey Collaboration ~ 1/14,000 Milky Way luminosity MV = -10.1 ~ 1/40,000 Milky Way luminosity ~ 1/1,000,000 Milky Way luminosity Ursa Major 1 Finding Invisible Galaxies bright faint blue red Willman et al 2002, Walsh, Willman & Jerjen 2009; see also e.g. Koposov et al 2008, Belokurov et al. Finding Invisible Galaxies Red, bright, cool bright Blue, hot, bright V-band apparent brightness V-band faint Red, faint, cool blue red From ARAA, V26, 1988 Willman et al 2002, Walsh, Willman & Jerjen 2009; see also e.g. Koposov et al 2008, Belokurov et al. Finding Invisible Galaxies Ursa Major I dwarf 1/1,000,000 MW luminosity Willman et al 2005 ~ 1/1,000,000 Milky Way luminosity Ursa Major 1 CMD of Ursa Major I Okamoto et al 2008 Distribution of the Milky Wayʼs dwarfs -14 Milky Way dwarfs 107 -12 -10 classical dwarfs V -8 5 10 Sun M L -6 ultra-faint dwarfs Canes Venatici II -4 Leo V Pisces II Willman I 1000 -2 Segue I 0 50 100 150 200 250 300
    [Show full text]
  • Asterion and Chara – the Confusion of the Chase
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Faculty Publications, UNL Libraries Libraries at University of Nebraska-Lincoln July 2002 Asterion and Chara – the Confusion of the Chase Charles D. Bernholz University of Nebraska-Lincoln, [email protected] Michael J. Lyons Follow this and additional works at: https://digitalcommons.unl.edu/libraryscience Part of the Library and Information Science Commons Bernholz, Charles D. and Lyons, Michael J., "Asterion and Chara – the Confusion of the Chase" (2002). Faculty Publications, UNL Libraries. 7. https://digitalcommons.unl.edu/libraryscience/7 This Article is brought to you for free and open access by the Libraries at University of Nebraska-Lincoln at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Faculty Publications, UNL Libraries by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. SPECIAL FEATURE: DEVELOPING IDEAS OF SPACE www.iop.org/journals/physed Asterion and Chara—the confusion of the chase Charles D Bernholz1 and Michael J Lyons2 1 Memorial Library, State University of New York College at Cortland, Cortland, NY 13045, USA 2 Port Jervis High School, Port Jervis, NY 12771, USA E-mail: [email protected] Abstract The study of astronomy, as an important part of any science education programme, provides our students with insights into more than just the cosmos. It may also serve as a mechanism to link them to other natural and social sciences. This article examines equally valid interpretations of the constellation Canes Venatici as an example of how the study of astronomy may serve this multidisciplinary educational role. In addition, it is an extension of the thoughts of Stannard (2001) on communicating physics through story.
    [Show full text]
  • Stsci Newsletter: 2011 Volume 028 Issue 02
    National Aeronautics and Space Administration Interacting Galaxies UGC 1810 and UGC 1813 Credit: NASA, ESA, and the Hubble Heritage Team (STScI/AURA) 2011 VOL 28 ISSUE 02 NEWSLETTER Space Telescope Science Institute We received a total of 1,007 proposals, after accounting for duplications Hubble Cycle 19 and withdrawals. Review process Proposal Selection Members of the international astronomical community review Hubble propos- als. Grouped in panels organized by science category, each panel has one or more “mirror” panels to enable transfer of proposals in order to avoid conflicts. In Cycle 19, the panels were divided into the categories of Planets, Stars, Stellar Rachel Somerville, [email protected], Claus Leitherer, [email protected], & Brett Populations and Interstellar Medium (ISM), Galaxies, Active Galactic Nuclei and Blacker, [email protected] the Inter-Galactic Medium (AGN/IGM), and Cosmology, for a total of 14 panels. One of these panels reviewed Regular Guest Observer, Archival, Theory, and Chronology SNAP proposals. The panel chairs also serve as members of the Time Allocation Committee hen the Cycle 19 Call for Proposals was released in December 2010, (TAC), which reviews Large and Archival Legacy proposals. In addition, there Hubble had already seen a full cycle of operation with the newly are three at-large TAC members, whose broad expertise allows them to review installed and repaired instruments calibrated and characterized. W proposals as needed, and to advise panels if the panelists feel they do not have The Advanced Camera for Surveys (ACS), Cosmic Origins Spectrograph (COS), the expertise to review a certain proposal. Fine Guidance Sensor (FGS), Space Telescope Imaging Spectrograph (STIS), and The process of selecting the panelists begins with the selection of the TAC Chair, Wide Field Camera 3 (WFC3) were all close to nominal operation and were avail- about six months prior to the proposal deadline.
    [Show full text]
  • Canes Venatici I Cloud of Galaxies Seen in the Hα Line
    A&A 479, 603–624 (2008) Astronomy DOI: 10.1051/0004-6361:20078652 & c ESO 2008 Astrophysics Canes Venatici I cloud of galaxies seen in the Hα line S. S. Kaisin and I. D. Karachentsev Special Astrophysical Observatory, Russian Academy of Sciences, N. Arkhyz, KChR, 369167, Russia e-mail: [email protected] Received 11 September 2007 / Accepted 25 September 2007 ABSTRACT We present results of Hα imaging for 42 galaxies in the nearby low-density cloud Canes Venatici I, populated mainly by late-type objects. Estimates of the Hα flux and integrated star formation rate (SFR) are now available for all 78 known members of this scattered system, spanning a large range in luminosity, surface brightness, HI content and SFR. Distributions of the CVnI galaxies versus their SFR, blue absolute magnitude and total hydrogen mass, are given in comparison with those for a population of the nearby virialized group around M 81. We found no essential correlation between star formation activity in a galaxy and its density environment. The bulk of CVnI galaxies had enough time to generate their baryon mass with the observed SFR. Most of them also possess a supply of gas that is sufficient to maintain their observed SFRs during the next Hubble time. Key words. galaxies: evolution – galaxies: ISM – galaxies: dwarf 1. Introduction 2. Observations and data reduction The distribution over the sky of 500 galaxies of the Local CCD images in the Hα-line and continuum were obtained for Volume, with distances within 10 Mpc, shows considerable in- 42 galaxies of the CVnI cloud during observing runs from March homogeneities due to the presence of groups and voids.
    [Show full text]
  • M31 Andromeda Galaxy Aq
    Constellation, Star, and Deep Sky Object Names Andromeda : M31 Andromeda Galaxy Lyra : Vega & M57 Ring Nebula Aquila : Altair Ophiuchus : Bernard’s Star Auriga : Capella Orion : Betelgeuse , Rigel & M42 Orion Nebula Bootes : Arcturus Perseus : Algol Cancer : M44 Beehive Cluster Sagittarius: Sagittarius A* Canes Venatici: M51 Whirlpool Galaxy Taurus : Aldebaran , Hyades Star Cluster , M1 Crab Nebula & Canis Major : Sirius M45 Pleiades Canis Minor : Procyon Tucana : Small Magellanic Cloud (SMC) Cassiopeia : Cassiopeia A & Tycho’s “Star” Ursa Minor : Polaris Centaurus : Proxima Centauri Virgo : Spica Dorado/Mensa : Large Magellanic Cloud (LMC) Milky Way Galaxy Gemini : Castor & Pollux Hercules : M13 Globular Cluster Characteristics of Stars (Compared with Sun) Class Color Temp. ( 1000 K) Absolute Magnitude Solar Luminosity Solar Mass Solar Diameter O Blue 60 -30 -7 1,000,000 50 100 to 1000 B Blue -White 30 -10 -3 10,000 10 10 to 100 A White 10 -7.5 +2 100 2 2 to 10 F White -Yellow 7.5 -6.5 +4 10 1.5 1 to 2 G Yellow 6.5 -4.5 +4.6 1 1 1 K Orange 4.5 -3.5 +11 1/100 0.5 0.5 M Red 3.5 -2.8 +15 1/100,000 0.08 0.1 Magnitude Magnitude scales: The smaller the magnitude number, the brighter the star Every 5 magnitudes = 100 times the brightness of object Every magnitude = 2.512 times the brightness of object Apparent magnitude = the brightness of object as seen from the viewer’s viewpoint (Earth) Absolute magnitude = “true brightness” – brightness as seen from 10 parsecs (32.6 light years) away Distance Measurement 1 astronomical unit = distance between Earth and Sun = 150 million kilometres or 93 million miles 1 light year ≈ 6 trillion miles / 9.5 trillion km Parsec = parallax second of arc – distance that a star “jumps” one second of a degree of arc in the sky as a result of the earth’s revolution around the sun.
    [Show full text]
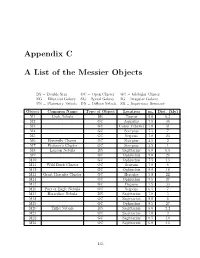
  • Appendix C a List of the Messier Objects
    Appendix C A List of the Messier Objects DS=DoubleStar OC=OpenCluster GC=GlobularCluster EG = Elliptical Galaxy SG = Spiral Galaxy IG = Irregular Galaxy PN = Planetary Nebula DN = Diffuse Nebula SR = Supernova Remnant Object Common Name Type of Object Location mv Dist. (kly) M1 Crab Nebula SR Taurus 9.0 6.3 M2 GC Aquarius 7.5 36 M3 GC Canes Venatici 7.0 31 M4 GC Scorpius 7.5 7 M5 GC Serpens 7.0 23 M6 Butterfly Cluster OC Scorpius 4.5 2 M7 Ptolemy’s Cluster OC Scorpius 3.5 1 M8 Lagoon Nebula DN Sagittarius 5.0 6.5 M9 GC Ophiuchus 9.0 26 M10 GC Ophiuchus 7.5 13 M11 Wild Duck Cluster OC Scutum 7.0 6 M12 GC Ophiuchus 8.0 18 M13 Great Hercules Cluster GC Hercules 5.8 22 M14 GC Ophiuchus 9.5 27 M15 GC Pegasus 7.5 33 M16 Part of Eagle Nebula OC Serpens 6.5 7 M17 Horseshoe Nebula DN Sagittarius 7.0 5 M18 OC Sagittarius 8.0 6 M19 GC Ophiuchus 8.5 27 M20 Trifid Nebula DN Sagittarius 5.0 2.2 M21 OC Sagittarius 7.0 3 M22 GC Sagittarius 6.5 10 M23 OC Sagittarius 6.0 4.5 135 Object Common Name Type of Object Location mv Dist. (kly) M24 Milky Way Patch Star cloud Sagittarius 11.5 10 M25 OC Sagittarius 4.9 2 M26 OC Scutum 9.5 5 M27 Dumbbell Nebula PN Vulpecula 7.5 1.25 M28 GC Sagittarius 8.5 18 M29 OC Cygnus 9.0 7.2 M30 GC Capricornus 8.5 25 M31 Andromeda Galaxy SG Andromeda 3.5 2500 M32 Satellite galaxy of M31 EG Andromeda 10.0 2900 M33 Triangulum Galaxy SG Triangulum 7.0 2590 M34 OC Perseus 6.0 1.4 M35 OC Gemini 5.5 2.8 M36 OC Auriga 6.5 4.1 M37 OC Auriga 6.0 4.6 M38 OC Auriga 7.0 4.2 M39 OC Cygnus 5.5 0.3 M40 Winnecke 4 DS Ursa Major 9.0 M41 OC Canis
    [Show full text]
  • Globular Clusters
    Observing Globular Clusters TAAS Astronomy 101 Jon Schuchardt August 2016 Outline • What are globular clusters? • Historical significance • Shapley-Sawyer classification M5 (Serpens Caput) • How to find, observe, and report on globular clusters What are Globular Star Clusters? • Densely packed, spherical agglomerations of 104 to 107 very old stars (12-14 billion years old) that surround a galactic nucleus • Most in the Milky Way are 10,000 to 50,000 light years away from us • Diameters: 10s to 100s of light years • Densities: average about 1 star per cubic light year, but more dense in the core • About 150 globular clusters known in the Milky Way What are Globular Star Clusters? • Some globular clusters, e.g., M15, have undergone gravitational collapse in their cores • Glob cores can be millions or even billions of times more densely populated than our solar neighborhood • Imagine a night sky with thousands of stars brighter than Sirius! • Black holes of low stellar mass (10-20 solar masses) may be common at the center of globular clusters. They have been detected (2012-2013) in M22 (a pair) and M62 by detecting radio emissions using the Very Large Array M62 (Ophiuchus) Easier to “see” the black holes using radio emissions and the VLA versus a Hubble view of M22 (Sagittarius) J. Strader et al., Nature Oct 4, 2012 Hertzsprung-Russell diagrams: Typical globular cluster (left) and M55 (right) Note the “knee”” H-R Diagram for M3 (Canes Venatici) The “knee” shows where stars begin to depart the Main Sequence on their path to becoming giants Can be used to estimate the age of the cluster “The thing’s hollow -- it goes on forever -- and -- oh my God! -- it’s full of stars!” Commander David Bowman 2001: A Space Odyssey Arthur C.
    [Show full text]
  • Astronomy 125 Syllabus
    Astronomy 125 – Observational Astronomy SEMESTER TIME DAY PLACE FALL 2012 12:00-12:50 p.m. T H Trafton C114 Clear evenings MTWH Standeford Observatory INSTRUCTOR: Dr. James Pierce office: TN N151; phone: 389-1114; office hours: M 12,1,2; T 10,1; W 12,1; H 10,1 email: [email protected]; web: http://mavdisk.mnsu.edu/jpierce/ COURSE MATERIALS: Mechler & Chartrand: National Audubon Society -- Constellations Dickinson et al: Mag 6 Star Atlas Edmund "Star and Planet Locator" Handouts (Download from my website) CONTENT: In this course we will study the night sky and various tools for observing it. We will concentrate on becoming familiar with constellations and bright stars, learning to read star charts, operating small telescopes, and discovering the variety of celestial objects available for observation. Approximate order of lecture topics: celestial sphere; coordinate systems; star charts; sidereal time; telescope optics; telescope specifications; astrophotography; lunar observations; planetary observations. Constellation lectures will be spread throughout the term. See my web page for a more detailed outline. ASSIGNMENTS: Several assignments will be given during the semester to help you become more familiar with the material. Written assignments will be due about a week after they are given out; points will be deducted for late assignments. Observing assignments (which must be done at the observatory) will run throughout the semester observing season. QUIZZES: Five constellation quizzes will be given during the semester; these will check your growing knowledge of the night sky. We will be studying constellations and their components, learning them in groups of six (see the constellation list).
    [Show full text]
  • Guide to the Constellations
    STAR DECK GUIDE TO THE CONSTELLATIONS BY MICHAEL K. SHEPARD, PH.D. ii TABLE OF CONTENTS Introduction 1 Constellations by Season 3 Guide to the Constellations Andromeda, Aquarius 4 Aquila, Aries, Auriga 5 Bootes, Camelopardus, Cancer 6 Canes Venatici, Canis Major, Canis Minor 7 Capricornus, Cassiopeia 8 Cepheus, Cetus, Coma Berenices 9 Corona Borealis, Corvus, Crater 10 Cygnus, Delphinus, Draco 11 Equuleus, Eridanus, Gemini 12 Hercules, Hydra, Lacerta 13 Leo, Leo Minor, Lepus, Libra, Lynx 14 Lyra, Monoceros 15 Ophiuchus, Orion 16 Pegasus, Perseus 17 Pisces, Sagitta, Sagittarius 18 Scorpius, Scutum, Serpens 19 Sextans, Taurus 20 Triangulum, Ursa Major, Ursa Minor 21 Virgo, Vulpecula 22 Additional References 23 Copyright 2002, Michael K. Shepard 1 GUIDE TO THE STAR DECK Introduction As an introduction to astronomy, you cannot go wrong by first learning the night sky. You only need a dark night, your eyes, and a good guide. This set of cards is not designed to replace an atlas, but to engage your interest and teach you the patterns, myths, and relationships between constellations. They may be used as “field cards” that you take outside with you, or they may be played in a variety of card games. The cultural and historical story behind the constellations is a subject all its own, and there are numerous books on the subject for the curious. These cards show 52 of the modern 88 constellations as designated by the International Astronomical Union. Many of them have remained unchanged since antiquity, while others have been added in the past century or so. The majority of these constellations are Greek or Roman in origin and often have one or more myths associated with them.
    [Show full text]
  • Spring Observing Notes
    Wynyard Planetarium & Observatory Spring Observing Notes Wynyard Planetarium & Observatory PUBLIC OBSERVING – Spring Tour of the Sky with the Naked Eye 2 1 Pointers Merak The Plough 4 Dubhe 5 Mizar Is Kochab Ursa Minor orange Kochab compared 3 to Polaris? Perseus Mirfak Polaris Pherkad 9 6 Algol Cassiopeia Look for the W shape delta 8 gamma 7 Notice how the constellations swing around Polaris during the night c Rob Peeling Feb-08 Figure 1: Sketch of the northern sky in spring North 1. On leaving the planetarium, turn around and look northwards over the roof of the building. Now look nearly straight above yourself and somewhat to your right and find a group of stars like the outline of a upside-down with its handle stretching to the right. This is the Plough (also called the Big Dipper) and is part of the constellation Ursa Major, the Great Bear. The top two stars are called the Pointers. 2. Use the Pointers to guide you downwards, to the next bright star. This is Polaris, the Pole (or North) Star. Note that it is not the brightest star in the sky, a common misconception. 3. Polaris, Kochab and Pherkad mark the constellation Ursa Minor, the Little Bear. To the right of Polaris are two prominent but fainter stars. These are Kochab and Pherkad, the Guardians of the Pole. Look carefully and you will notice that Kochab is slightly orange when compared to Polaris. Check with binoculars. Not all stars are white. The colour © Rob Peeling, CaDAS, 2008 Wynyard Planetarium & Observatory PUBLIC OBSERVING – Spring shows that Kochab is cooler than Polaris in the same way that red-hot is cooler than white-hot.
    [Show full text]
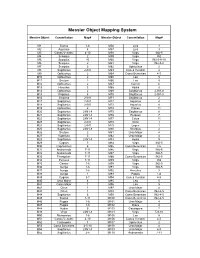
  • Messier Object Mapping System
    Messier Object Mapping System Messier Object Constellation Map# Messier Object Constellation Map# M1 Taurus 1-6 M56 Lyra 3 M2 Aquarius 8 M57 Lyra 3 M3 Canes Venatici 4-10 M58 Virgo IN2-5 M4 Scorpius 2 M59 Virgo IN2 M5 Scorpius 10 M60 Virgo IN2-5-9-10 M6 Scorpius 2 M61 Virgo IN2-5-8 M7 Scorpius 2 M62 Ophiuchus 2 M8 Sagittarius 2-IN1 M63 Canes Venatici 4 M9 Ophiuchus 2 M64 Coma Berenices 4-5 M10 Ophiuchus 2 M65 Leo 5 M11 Scutum 2 M66 Leo 5 M12 Ophiuchus 2 M67 Cancer 6 M13 Hercules 3 M68 Hydra 9 M14 Ophiuchus 2 M69 Sagittarius 2-IN1-8 M15 Pegasus 8 M70 Sagittarius 2-IN1-8 M16 Serpens 2-IN1 M71 Sagittarius 2 M17 Sagittarius 2-IN1 M72 Aquarius 8 M18 Sagittarius 2-IN1 M73 Aquarius 8 M19 Ophiuchus 2 M74 Pisces 11 M20 Sagittarius 2-IN1-8 M75 Sagittarius 8 M21 Sagittarius 2-IN1-8 M76 Perseus 7 M22 Sagittarius 2-IN1-8 M77 Cetus 11 M23 Sagittarius 2-IN1 M78 Orion 1 M24 Sagittarius 2-IN1 M79 Lepus 1 M25 Sagittarius 2-IN1-8 M80 Scorpius 2 M26 Scutum 2 M81 Ursa Major 4 M27 Vupecula 3 M82 Ursa Major 4 M28 Sagittarius 2-IN1-8 M83 Hydra 9 M29 Cygnus 3 M84 Virgo IN2-5 M30 Capricornus 8 M85 Coma Berenices 4-5 M31 Andromeda 7-11 M86 Virgo IN2-5 M32 Andromeda 7-11 M87 Virgo IN2-5 M33 Triangulum 7-11 M88 Coma Berenices IN2-5 M34 Perseus 7-11 M89 Virgo IN2 M35 Gemini 1-6 M90 Virgo IN2-5 M36 Auriga 1-6 M91 Virgo IN2-5 M37 Auriga 1-6 M92 Hercules 3 M38 Auriga 1 M93 Puppis 1-6 M39 Cygnus 3-7 M94 Canes Venatici 4-5 M40 Ursa Major 4 M95 Leo 5 M41 Canis Major 1 M96 Leo 5 M42 Orion 1 M97 Ursa Major 4 M43 Orion 1 M98 Coma Berenices IN2-4-5 M44 Sagittarius 6 M99 Coma Berenices IN2-4-5 M45 Taurus 1-11 M100 Coma Berenices IN2-4-5 M46 Puppis 1-6 M101 Ursa Major 4 M47 Puppis 1-6 M102 Draco 4 M48 Hydra 6 M103 Cassiopeia 7 M49 Virgo 2-IN1-8 M104 Virgo 5-9-10 M50 Monoceros 1-6 M105 Leo 5 M51 Canes Venatici 4-10 M106 Canes Venatici 4-5 M52 Cassiopeia 7 M107 Ophiuchus 2 M53 Coma Berenices 4-5-10 M108 Ursa Major 4 M54 Sagittarius 2-IN1-8 M109 Ursa Major 4-5 M55 Sagittarius 2-8 M110 Andromeda 7-11 Messier Object List # NGC# Constellation Type Name, If Any Mag.
    [Show full text]