DOCSLIB.ORG

Properties of Least Squares Estimators Simple Linear Regression Model: Y = Β 0 + Β1x + Ε • Ε Is the Random Error So Y Is A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Properties of Least Squares Estimators Simple Linear Regression Model: Y = Β 0 + Β1x + Ε • Ε Is the Random Error So Y Is A Properties of Least Squares Estimators Simple Linear Regression Model: Y = β0 + β1x + is the random error so Y is a random variable too. • Sample: (x1;Y1); (x2;Y2);:::; (xn;Yn) Each (xi;Yi) satisfies Yi = β0 + β1xi + i Least Squares Estimators: n ^ i=1(xi x)(Yi Y ) ^ ^ β1 = P n − −2 ; β0 = Y β1x (xi x) − Pi=1 − 1 Properties of Least Squares Estimators Assumptions on the Random Error E[i] = 0 • 2 V (i) = σ • Implications for the Response Variable Y E[Yi] = β0 + β1xi • 2 V (Yi) = σ • What can be said about: ^ E[β1]? • ^ V (β1)? • ^ E[β0]? • ^ V (β0)? • ^ ^ Cov(β0; β1)? • 2 Properties of Least Squares Estimators ^ ^ Proposition: The estimators β0 and β1 are unbiased; that is, ^ ^ E[β0] = β0;E[β1] = β1: Proof: n ^ i=1(xi x)(Yi Y ) β1 = P n − −2 (xi x) Pi=1 − n n i=1(xi x)Yi Y i=1(xi x) = P − n − P2 − (xi x) Pi=1 − n i=1(xi x)Yi = P n − 2 (xi x) Pi=1 − 3 Thus n ^ (xi x) E[β1] = n − 2 E[Yi] X (xi x) i=1 Pi=1 − n (xi x) = n − 2 (β0 + β1xi) X (xi x) i=1 Pi=1 − n n i=1(xi x) i=1(xi x)xi = Pn − 2 β0 + β1P n − 2 (xi x) (xi x) Pi=1 − Pi=1 − ^ ^ E[β0] = E[Y β1x] − 1 n = E[Y ] E[β^ ]x n X i 1 i=1 − 1 n 1 n = (β + β x ) β x n X 0 1 i 1n X i i=1 − i=1 4 Properties of Least Squares Estimators ^ ^ Proposition: The variances of β0 and β1 are: 2 n 2 2 n 2 ^ σ i=1 xi σ i=1 xi V (β0) = n P 2 = P (xi x) Sxx Pi=1 − and 2 2 ^ σ σ V (β1) = n 2 = : (xi x) Sxx Pi=1 − Proof: n ^ i=1(xi x)Yi V (β1) = V P − Sxx 2 n 1 2 = (xi x) V (Yi) S X xx i=1 − 2 n 1 2 2 = (xi x) ! σ S X xx i=1 − 1 = σ2 Sxx 5 ^ ^ V (β0) = V (Y β1x) − ^ ^ = V (Y ) + V ( β1x) + 2Cov(Y; xβ1) − − 2 ^ ^ = V (Y ) + x V (β1) 2xCov(Y; β1) − 2 2 σ 2 σ ^ = + x 2xCov(Y; β1) n Sxx − Now let's evaluate the covariance term: n n 0 1 xj x 1 Cov(Y; β^ ) = Cov Y ; − Y 1 X n i X S j @ i=1 j=1 xx A n n xj x = − Cov(Y ;Y ) X X nS i j i=1 j=1 xx n xi x = − σ2 + 0 X nS i=1 xx = 0 6 Thus 2 2 ^ σ 2 σ V (β0) = + x n Sxx S + nx2 = σ2 xx nSxx n 2 2 (xi x) + nx = σ2 Pi=1 − nSxx n 2 2 2 (x 2xxi + x ) + nx = σ2 Pi=1 i − nSxx n x2 = σ2 Pi=1 i nSxx 7 Properties of Least Squares Estimators A Practical Matter The variance σ2 of the random error is usually not known. So it is necessary to esti- mate it. Proposition: The estimator n 2 1 2 1 S = (Yi Y^i) = SSE n 2 X − n 2 − i=1 − is an unbiased estimator of σ2. 8 Properties of Least Squares Estimators Assumptions on the Random Error E[i] = 0 • 2 V (i) = σ • Each i is normally distributed. • Implications for the Estimators ^ β1 is normally distributed with mean β1 and variance 2 • σ ; Sxx ^ β0 is normally distributed with mean β0 and variance n 2 • 2 i=1 x σ P i ; nSxx (n 2)S2 2 −σ2 has a χ distribution with n 2 degrees of free- • dom; − 2 ^ ^ S is independent of β0 and β1. • 9 Properties of Least Squares Estimators Multiple Linear Regression Model: Y = β0 + β1x1 + + βkxk + ··· Sample: (x11; x12; : : : ; x1k;Y1) (x21; x22; : : : ; x2k;Y2) . (xn1; xn2; : : : ; xnk;Yn) Each (xi;Yi) satisfies Yi = β0+β1xi+ +βkxk+i ··· Least Squares Estimators: 1 β^ = (X0X)− X0Y 10 Properties of Least Squares Estimators ^ ^ Each βi is an unbiased estimator of βi: E[βi] = βi; • ^ 2 V (βi) = ciiσ , where cii is the element in the ith row • 1 and ith column of (X0X)− ; ^ ^ 2 Cov(βi; βi) = cijσ ; • The estimator • ^ SSE Y0Y β0X0Y S2 = = − n (k + 1) n (k + 1) − − is an unbiased estimator of σ2. 11 Properties of Least Squares Estimators When is normally distributed, ^ Each βi is normally distributed; • The random variable • (n (k + 1))S2 − σ2 has a χ2 distribution with n (k +1) degrees of freee- dom; − 2 ^ The statistics S and βi, i = 0; 1; : : : ; k, are indepen- • dent. 12.
Load more

Recommended publications
  • Generalized Linear Models and Generalized Additive Models
    00:34 Friday 27th February, 2015 Copyright ©Cosma Rohilla Shalizi; do not distribute without permission updates at http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/ Chapter 13 Generalized Linear Models and Generalized Additive Models [[TODO: Merge GLM/GAM and Logistic Regression chap- 13.1 Generalized Linear Models and Iterative Least Squares ters]] [[ATTN: Keep as separate Logistic regression is a particular instance of a broader kind of model, called a gener- chapter, or merge with logis- alized linear model (GLM). You are familiar, of course, from your regression class tic?]] with the idea of transforming the response variable, what we’ve been calling Y , and then predicting the transformed variable from X . This was not what we did in logis- tic regression. Rather, we transformed the conditional expected value, and made that a linear function of X . This seems odd, because it is odd, but it turns out to be useful. Let’s be specific. Our usual focus in regression modeling has been the condi- tional expectation function, r (x)=E[Y X = x]. In plain linear regression, we try | to approximate r (x) by β0 + x β. In logistic regression, r (x)=E[Y X = x] = · | Pr(Y = 1 X = x), and it is a transformation of r (x) which is linear. The usual nota- tion says | ⌘(x)=β0 + x β (13.1) · r (x) ⌘(x)=log (13.2) 1 r (x) − = g(r (x)) (13.3) defining the logistic link function by g(m)=log m/(1 m). The function ⌘(x) is called the linear predictor. − Now, the first impulse for estimating this model would be to apply the transfor- mation g to the response.
    [Show full text]
  • Generalized and Weighted Least Squares Estimation
    LINEAR REGRESSION ANALYSIS MODULE – VII Lecture – 25 Generalized and Weighted Least Squares Estimation Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur 2 The usual linear regression model assumes that all the random error components are identically and independently distributed with constant variance. When this assumption is violated, then ordinary least squares estimator of regression coefficient looses its property of minimum variance in the class of linear and unbiased estimators. The violation of such assumption can arise in anyone of the following situations: 1. The variance of random error components is not constant. 2. The random error components are not independent. 3. The random error components do not have constant variance as well as they are not independent. In such cases, the covariance matrix of random error components does not remain in the form of an identity matrix but can be considered as any positive definite matrix. Under such assumption, the OLSE does not remain efficient as in the case of identity covariance matrix. The generalized or weighted least squares method is used in such situations to estimate the parameters of the model. In this method, the deviation between the observed and expected values of yi is multiplied by a weight ω i where ω i is chosen to be inversely proportional to the variance of yi. n 2 For simple linear regression model, the weighted least squares function is S(,)ββ01=∑ ωii( yx −− β0 β 1i) . ββ The least squares normal equations are obtained by differentiating S (,) ββ 01 with respect to 01 and and equating them to zero as nn n ˆˆ β01∑∑∑ ωβi+= ωiixy ω ii ii=11= i= 1 n nn ˆˆ2 βω01∑iix+= βω ∑∑ii x ω iii xy.
    [Show full text]
  • 18.650 (F16) Lecture 10: Generalized Linear Models (Glms)
    Statistics for Applications Chapter 10: Generalized Linear Models (GLMs) 1/52 Linear model A linear model assumes Y X (µ(X), σ2I), | ∼ N And ⊤ IE(Y X) = µ(X) = X β, | 2/52 Components of a linear model The two components (that we are going to relax) are 1. Random component: the response variable Y X is continuous | and normally distributed with mean µ = µ(X) = IE(Y X). | 2. Link: between the random and covariates X = (X(1),X(2), ,X(p))⊤: µ(X) = X⊤β. · · · 3/52 Generalization A generalized linear model (GLM) generalizes normal linear regression models in the following directions. 1. Random component: Y some exponential family distribution ∼ 2. Link: between the random and covariates: ⊤ g µ(X) = X β where g called link function� and� µ = IE(Y X). | 4/52 Example 1: Disease Occuring Rate In the early stages of a disease epidemic, the rate at which new cases occur can often increase exponentially through time. Hence, if µi is the expected number of new cases on day ti, a model of the form µi = γ exp(δti) seems appropriate. ◮ Such a model can be turned into GLM form, by using a log link so that log(µi) = log(γ) + δti = β0 + β1ti. ◮ Since this is a count, the Poisson distribution (with expected value µi) is probably a reasonable distribution to try. 5/52 Example 2: Prey Capture Rate(1) The rate of capture of preys, yi, by a hunting animal, tends to increase with increasing density of prey, xi, but to eventually level off, when the predator is catching as much as it can cope with.
    [Show full text]
  • 4.3 Least Squares Approximations
    218 Chapter 4. Orthogonality 4.3 Least Squares Approximations It often happens that Ax D b has no solution. The usual reason is: too many equations. The matrix has more rows than columns. There are more equations than unknowns (m is greater than n). The n columns span a small part of m-dimensional space. Unless all measurements are perfect, b is outside that column space. Elimination reaches an impossible equation and stops. But we can’t stop just because measurements include noise. To repeat: We cannot always get the error e D b Ax down to zero. When e is zero, x is an exact solution to Ax D b. When the length of e is as small as possible, bx is a least squares solution. Our goal in this section is to compute bx and use it. These are real problems and they need an answer. The previous section emphasized p (the projection). This section emphasizes bx (the least squares solution). They are connected by p D Abx. The fundamental equation is still ATAbx D ATb. Here is a short unofficial way to reach this equation: When Ax D b has no solution, multiply by AT and solve ATAbx D ATb: Example 1 A crucial application of least squares is fitting a straight line to m points. Start with three points: Find the closest line to the points .0; 6/; .1; 0/, and .2; 0/. No straight line b D C C Dt goes through those three points. We are asking for two numbers C and D that satisfy three equations.
    [Show full text]
  • Time-Series Regression and Generalized Least Squares in R*
    Time-Series Regression and Generalized Least Squares in R* An Appendix to An R Companion to Applied Regression, third edition John Fox & Sanford Weisberg last revision: 2018-09-26 Abstract Generalized least-squares (GLS) regression extends ordinary least-squares (OLS) estimation of the normal linear model by providing for possibly unequal error variances and for correlations between different errors. A common application of GLS estimation is to time-series regression, in which it is generally implausible to assume that errors are independent. This appendix to Fox and Weisberg (2019) briefly reviews GLS estimation and demonstrates its application to time-series data using the gls() function in the nlme package, which is part of the standard R distribution. 1 Generalized Least Squares In the standard linear model (for example, in Chapter 4 of the R Companion), E(yjX) = Xβ or, equivalently y = Xβ + " where y is the n×1 response vector; X is an n×k +1 model matrix, typically with an initial column of 1s for the regression constant; β is a k + 1 ×1 vector of regression coefficients to estimate; and " is 2 an n×1 vector of errors. Assuming that " ∼ Nn(0; σ In), or at least that the errors are uncorrelated and equally variable, leads to the familiar ordinary-least-squares (OLS) estimator of β, 0 −1 0 bOLS = (X X) X y with covariance matrix 2 0 −1 Var(bOLS) = σ (X X) More generally, we can assume that " ∼ Nn(0; Σ), where the error covariance matrix Σ is sym- metric and positive-definite. Different diagonal entries in Σ error variances that are not necessarily all equal, while nonzero off-diagonal entries correspond to correlated errors.
    [Show full text]
  • Statistical Properties of Least Squares Estimates
    1 STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS Recall: Assumption: E(Y|x) = η0 + η1x (linear conditional mean function) Data: (x1, y1), (x2, y2), … , (xn, yn) ˆ Least squares estimator: E (Y|x) = "ˆ 0 +"ˆ 1 x, where SXY "ˆ = "ˆ = y -"ˆ x 1 SXX 0 1 2 SXX = ∑ ( xi - x ) = ∑ xi( xi - x ) SXY = ∑ ( xi - x ) (yi - y ) = ∑ ( xi - x ) yi Comments: 1. So far we haven’t used any assumptions about conditional variance. 2. If our data were the entire population, we could also use the same least squares procedure to fit an approximate line to the conditional sample means. 3. Or, if we just had data, we could fit a line to the data, but nothing could be inferred beyond the data. 4. (Assuming again that we have a simple random sample from the population.) If we also assume e|x (equivalently, Y|x) is normal with constant variance, then the least squares estimates are the same as the maximum likelihood estimates of η0 and η1. Properties of "ˆ 0 and "ˆ 1 : n #(xi " x )yi n n SXY i=1 (xi " x ) 1) "ˆ 1 = = = # yi = "ci yi SXX SXX i=1 SXX i=1 (x " x ) where c = i i SXX Thus: If the xi's are fixed (as in the blood lactic acid example), then "ˆ 1 is a linear ! ! ! combination of the yi's. Note: Here we want to think of each y as a random variable with distribution Y|x . Thus, ! ! ! ! ! i i ! if the yi’s are independent and each Y|xi is normal, then "ˆ 1 is also normal.
    [Show full text]
  • Models Where the Least Trimmed Squares and Least Median of Squares Estimators Are Maximum Likelihood
    Models where the Least Trimmed Squares and Least Median of Squares estimators are maximum likelihood Vanessa Berenguer-Rico, Søren Johanseny& Bent Nielsenz 1 September 2019 Abstract The Least Trimmed Squares (LTS) and Least Median of Squares (LMS) estimators are popular robust regression estimators. The idea behind the estimators is to …nd, for a given h; a sub-sample of h ‘good’observations among n observations and esti- mate the regression on that sub-sample. We …nd models, based on the normal or the uniform distribution respectively, in which these estimators are maximum likelihood. We provide an asymptotic theory for the location-scale case in those models. The LTS estimator is found to be h1=2 consistent and asymptotically standard normal. The LMS estimator is found to be h consistent and asymptotically Laplace. Keywords: Chebychev estimator, LMS, Uniform distribution, Least squares esti- mator, LTS, Normal distribution, Regression, Robust statistics. 1 Introduction The Least Trimmed Squares (LTS) and the Least Median of Squares (LMS) estimators sug- gested by Rousseeuw (1984) are popular robust regression estimators. They are de…ned as follows. Consider a sample with n observations, where some are ‘good’and some are ‘out- liers’. The user chooses a number h and searches for a sub-sample of h ‘good’observations. The idea is to …nd the sub-sample with the smallest residual sum of squares –for LTS –or the least maximal squared residual –for LMS. In this paper, we …nd models in which these estimators are maximum likelihood. In these models, we …rst draw h ‘good’regression errors from a normal distribution, for LTS, or a uniform distribution, for LMS.
    [Show full text]
  • Testing for Heteroskedastic Mixture of Ordinary Least 5
    TESTING FOR HETEROSKEDASTIC MIXTURE OF ORDINARY LEAST 5. SQUARES ERRORS Chamil W SENARATHNE1 Wei JIANGUO2 Abstract There is no procedure available in the existing literature to test for heteroskedastic mixture of distributions of residuals drawn from ordinary least squares regressions. This is the first paper that designs a simple test procedure for detecting heteroskedastic mixture of ordinary least squares residuals. The assumption that residuals must be drawn from a homoscedastic mixture of distributions is tested in addition to detecting heteroskedasticity. The test procedure has been designed to account for mixture of distributions properties of the regression residuals when the regressor is drawn with reference to an active market. To retain efficiency of the test, an unbiased maximum likelihood estimator for the true (population) variance was drawn from a log-normal normal family. The results show that there are significant disagreements between the heteroskedasticity detection results of the two auxiliary regression models due to the effect of heteroskedastic mixture of residual distributions. Forecasting exercise shows that there is a significant difference between the two auxiliary regression models in market level regressions than non-market level regressions that supports the new model proposed. Monte Carlo simulation results show significant improvements in the model performance for finite samples with less size distortion. The findings of this study encourage future scholars explore possibility of testing heteroskedastic mixture effect of residuals drawn from multiple regressions and test heteroskedastic mixture in other developed and emerging markets under different market conditions (e.g. crisis) to see the generalisatbility of the model. It also encourages developing other types of tests such as F-test that also suits data generating process.
    [Show full text]
  • 1 Simple Linear Regression I – Least Squares Estimation
    1 Simple Linear Regression I – Least Squares Estimation Textbook Sections: 18.1–18.3 Previously, we have worked with a random variable x that comes from a population that is normally distributed with mean µ and variance σ2. We have seen that we can write x in terms of µ and a random error component ε, that is, x = µ + ε. For the time being, we are going to change our notation for our random variable from x to y. So, we now write y = µ + ε. We will now find it useful to call the random variable y a dependent or response variable. Many times, the response variable of interest may be related to the value(s) of one or more known or controllable independent or predictor variables. Consider the following situations: LR1 A college recruiter would like to be able to predict a potential incoming student’s first–year GPA (y) based on known information concerning high school GPA (x1) and college entrance examination score (x2). She feels that the student’s first–year GPA will be related to the values of these two known variables. LR2 A marketer is interested in the effect of changing shelf height (x1) and shelf width (x2)on the weekly sales (y) of her brand of laundry detergent in a grocery store. LR3 A psychologist is interested in testing whether the amount of time to become proficient in a foreign language (y) is related to the child’s age (x). In each case we have at least one variable that is known (in some cases it is controllable), and a response variable that is a random variable.
    [Show full text]
  • The Simple Linear Regression Model
    Simple Linear 12 Regression Material from Devore’s book (Ed 8), and Cengagebrain.com The Simple Linear Regression Model The simplest deterministic mathematical relationship between two variables x and y is a linear relationship: y = β0 + β1x. The objective of this section is to develop an equivalent linear probabilistic model. If the two (random) variables are probabilistically related, then for a fixed value of x, there is uncertainty in the value of the second variable. So we assume Y = β0 + β1x + ε, where ε is a random variable. 2 variables are related linearly “on average” if for fixed x the actual value of Y differs from its expected value by a random amount (i.e. there is random error). 2 A Linear Probabilistic Model Definition The Simple Linear Regression Model 2 There are parameters β0, β1, and σ , such that for any fixed value of the independent variable x, the dependent variable is a random variable related to x through the model equation Y = β0 + β1x + ε The quantity ε in the model equation is the ERROR -- a random variable, assumed to be symmetrically distributed with 2 2 E(ε) = 0 and V(ε) = σ ε = σ (no assumption made about the distribution of ε, yet) 3 A Linear Probabilistic Model X: the independent, predictor, or explanatory variable (usually known). Y: The dependent or response variable. For fixed x, Y will be random variable. ε: The random deviation or random error term. For fixed x, ε will be random variable. What exactly does ε do? 4 A Linear Probabilistic Model The points (x1, y1), …, (xn, yn) resulting from n independent observations will then be scattered about the true regression line: This image cannot currently be displayed.
    [Show full text]
  • Chapter 7 Least Squares Estimation
    7-1 Least Squares Estimation Version 1.3 Chapter 7 Least Squares Estimation 7.1. Introduction Least squares is a time-honored estimation procedure, that was developed independently by Gauss (1795), Legendre (1805) and Adrain (1808) and published in the first decade of the nineteenth century. It is perhaps the most widely used technique in geophysical data analysis. Unlike maximum likelihood, which can be applied to any problem for which we know the general form of the joint pdf, in least squares the parameters to be estimated must arise in expressions for the means of the observations. When the parameters appear linearly in these expressions then the least squares estimation problem can be solved in closed form, and it is relatively straightforward to derive the statistical properties for the resulting parameter estimates. One very simple example which we will treat in some detail in order to illustrate the more general problem is that of fitting a straight line to a collection of pairs of observations (xi, yi) where i = 1, 2, . , n. We suppose that a reasonable model is of the form y = β0 + β1x, (1) and we need a mechanism for determining β0 and β1. This is of course just a special case of many more general problems including fitting a polynomial of order p, for which one would need to find p + 1 coefficients. The most commonly used method for finding a model is that of least squares estimation. It is supposed that x is an independent (or predictor) variable which is known exactly, while y is a dependent (or response) variable.
    [Show full text]
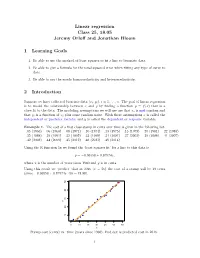
  • Reading 25: Linear Regression
    Linear regression Class 25, 18.05 Jeremy Orloff and Jonathan Bloom 1 Learning Goals 1. Be able to use the method of least squares to fit a line to bivariate data. 2. Be able to give a formula for the total squared error when fitting any type of curve to data. 3. Be able to say the words homoscedasticity and heteroscedasticity. 2 Introduction Suppose we have collected bivariate data (xi; yi), i = 1; : : : ; n. The goal of linear regression is to model the relationship between x and y by finding a function y = f(x) that is a close fit to the data. The modeling assumptions we will use are that xi is not random and that yi is a function of xi plus some random noise. With these assumptions x is called the independent or predictor variable and y is called the dependent or response variable. Example 1. The cost of a first class stamp in cents over time is given in the following list. .05 (1963) .06 (1968) .08 (1971) .10 (1974) .13 (1975) .15 (1978) .20 (1981) .22 (1985) .25 (1988) .29 (1991) .32 (1995) .33 (1999) .34 (2001) .37 (2002) .39 (2006) .41 (2007) .42 (2008) .44 (2009) .45 (2012) .46 (2013) .49 (2014) Using the R function lm we found the ‘least squares fit’ for a line to this data is y = −0:06558 + 0:87574x; where x is the number of years since 1960 and y is in cents. Using this result we ‘predict’ that in 2016 (x = 56) the cost of a stamp will be 49 cents (since −0:06558 + 0:87574x · 56 = 48:98).
    [Show full text]