Finding Pareto Optimal Groups: Group-Based Skyline
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2018-19 Phoenix Suns Media Guide 2018-19 Suns Schedule
2018-19 PHOENIX SUNS MEDIA GUIDE 2018-19 SUNS SCHEDULE OCTOBER 2018 JANUARY 2019 SUN MON TUE WED THU FRI SAT SUN MON TUE WED THU FRI SAT 1 SAC 2 3 NZB 4 5 POR 6 1 2 PHI 3 4 LAC 5 7:00 PM 7:00 PM 7:00 PM 7:00 PM 7:00 PM PRESEASON PRESEASON PRESEASON 7 8 GSW 9 10 POR 11 12 13 6 CHA 7 8 SAC 9 DAL 10 11 12 DEN 7:00 PM 7:00 PM 6:00 PM 7:00 PM 6:30 PM 7:00 PM PRESEASON PRESEASON 14 15 16 17 DAL 18 19 20 DEN 13 14 15 IND 16 17 TOR 18 19 CHA 7:30 PM 6:00 PM 5:00 PM 5:30 PM 3:00 PM ESPN 21 22 GSW 23 24 LAL 25 26 27 MEM 20 MIN 21 22 MIN 23 24 POR 25 DEN 26 7:30 PM 7:00 PM 5:00 PM 5:00 PM 7:00 PM 7:00 PM 7:00 PM 28 OKC 29 30 31 SAS 27 LAL 28 29 SAS 30 31 4:00 PM 7:30 PM 7:00 PM 5:00 PM 7:30 PM 6:30 PM ESPN FSAZ 3:00 PM 7:30 PM FSAZ FSAZ NOVEMBER 2018 FEBRUARY 2019 SUN MON TUE WED THU FRI SAT SUN MON TUE WED THU FRI SAT 1 2 TOR 3 1 2 ATL 7:00 PM 7:00 PM 4 MEM 5 6 BKN 7 8 BOS 9 10 NOP 3 4 HOU 5 6 UTA 7 8 GSW 9 6:00 PM 7:00 PM 7:00 PM 5:00 PM 7:00 PM 7:00 PM 7:00 PM 11 12 OKC 13 14 SAS 15 16 17 OKC 10 SAC 11 12 13 LAC 14 15 16 6:00 PM 7:00 PM 7:00 PM 4:00 PM 8:30 PM 18 19 PHI 20 21 CHI 22 23 MIL 24 17 18 19 20 21 CLE 22 23 ATL 5:00 PM 6:00 PM 6:30 PM 5:00 PM 5:00 PM 25 DET 26 27 IND 28 LAC 29 30 ORL 24 25 MIA 26 27 28 2:00 PM 7:00 PM 8:30 PM 7:00 PM 5:30 PM DECEMBER 2018 MARCH 2019 SUN MON TUE WED THU FRI SAT SUN MON TUE WED THU FRI SAT 1 1 2 NOP LAL 7:00 PM 7:00 PM 2 LAL 3 4 SAC 5 6 POR 7 MIA 8 3 4 MIL 5 6 NYK 7 8 9 POR 1:30 PM 7:00 PM 8:00 PM 7:00 PM 7:00 PM 7:00 PM 8:00 PM 9 10 LAC 11 SAS 12 13 DAL 14 15 MIN 10 GSW 11 12 13 UTA 14 15 HOU 16 NOP 7:00 -
2019-20 Immaculate Basketball Checklist
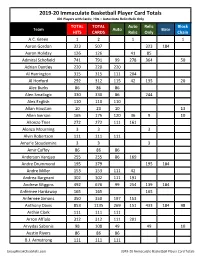
2019-20 Immaculate Basketball Player Card Totals 401 Players with Cards; Hits = Auto+Auto Relic+Relic Only TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain A.C. Green 1 2 1 1 Aaron Gordon 323 507 323 184 Aaron Holiday 126 126 41 85 Admiral Schofield 741 791 99 278 364 50 Adrian Dantley 220 220 220 Al Harrington 315 315 111 204 Al Horford 292 312 115 42 135 20 Alec Burks 86 86 86 Alen Smailagic 330 330 86 244 Alex English 110 110 110 Allan Houston 10 23 10 13 Allen Iverson 165 175 120 36 9 10 Allonzo Trier 272 272 111 161 Alonzo Mourning 3 3 3 Alvin Robertson 111 111 111 Amar'e Stoudemire 3 3 3 Amir Coffey 86 86 86 Anderson Varejao 255 255 86 169 Andre Drummond 195 379 195 184 Andre Miller 153 153 111 42 Andrea Bargnani 302 302 111 191 Andrew Wiggins 492 676 99 254 139 184 Anfernee Hardaway 165 165 165 Anfernee Simons 350 350 197 153 Anthony Davis 853 1135 269 151 433 184 98 Archie Clark 111 111 111 Arron Afflalo 312 312 111 201 Arvydas Sabonis 98 108 49 49 10 Austin Rivers 86 86 86 B.J. Armstrong 111 111 111 GroupBreakChecklists.com 2019-20 Immaculate Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain Bam Adebayo 163 347 163 184 Baron Davis 98 118 98 20 Ben Simmons 206 390 5 201 184 Bernard King 230 233 230 3 Bill Laimbeer 4 4 4 Bill Russell 104 117 104 13 Bill Walton 35 48 35 13 Blake Griffin 318 502 5 313 184 Bob McAdoo 49 59 49 10 Boban Marjanovic 264 264 111 153 Bogdan Bogdanovic 184 190 141 42 1 6 Bojan Bogdanovic 247 431 247 184 Bol Bol 719 768 99 287 333 -

Cavalier Classic 1996 Round 1 Tossups
Cavalier Classic 1996 Round 1 Tossups: 1) At the age of 14, he left high school to enter a seminary, but dropped out a year later. After a knee injury forced him off his high school wrestling team, he took up acting, and made his film debut in 1981's Endless Love. FfP, identify this actor, born Thomas Mapother, whose films include Born on the Fourth of July, Top Gun, and Mission: Impossible. Answer: Tom _Cruise_ 2) Lady Astor became the first female member of the House of Commons. The Bauhaus was established, and the Amritsar massacre took place. FfP, identify the common year, in which Hitler established the Nazi party, the Soviet Union was founded, and the Treaty of Versailles was signed. 3) A reservoir for erythrocytes, it regulates the number of them in circulation, destroys old ones, and stores the iron that they contain. In addition, it produces lymphocytes and breaks down foreign particles. FfP, identify this organ, an aggregate of lymphoid tissue which lies behind the stomach. Answer: _spleen_ 4) His apocryphal acts tell how he died by crucifixion in Achaia. He lived as a fisherman in Beth-saida with his brother Simon Peter until becoming a follower of John the Baptist. FTP, identify this disciple, the patron saint of Scotland. Answer: _Andrew_ 5) He founded a literary review in 1935 while on assignment in Spain. A translator of Blake, he wrote social poems collected in Extravagaria, Canto general, and Residence on Earth. FTP, name this poet, who returned to Chile in 1953, the winner of the 1971 Nobel Prize who figured in the film II Postino. -

Wliolesale Price Index up Slightly in March
. c The weather Inside today R((in with heavy downpours at times, high in the 40s, low tonight in the 40s. Area news ,.14-15 Editorial . .......4 Rain likely Friday, high about 50. Business.. .... 17 . .12-13 National weather forecast map on Classified . ..19-20 Gardening .... 18 Page 20. Comics .,. .... 21 Obituaries .......8 TWENTV/rWO PAGEd “The Bright One'* Dear Abby .... 21 Sports — .. .9-10 THREE SECTIONS • f 'V: MANCHESTER, CONN.> THURSDAY. APRIL 1. 1976- VOL. XCV. No. 155 PRICE) FIETEEN CENTS >; Farm prices down Wliolesale price index up slightly in March WASHINGTON (UPI)-Wholesale products, cereal and bakery products for raw farm products fell 1.5 per prices rose 0.2 per cent in March as and meat. The decline in meat cent in the month ending March 15, rising costs of industrial goods and prices, however, was less than in the largely because of lower prices for processed foods overshadowed a previous month: cattle, hogs, milk and eggs. drop in prices for farm products, the The rise in industrial commodities, Fluctuations in prices for raw farm Labor Department reported today. which make upmost of the index, was products usually are reflected first in The 1 per cent decline in farm much greater than a 0.1 per cent in the wholesale market and then on product prices was less than in re crease during the previous month, retail shelves. cent months, the department said. Lumber and wood prices rose more Larry Summers, a department Industrial commodities rose 0.4 per than in Febuary and prices for hides, food economist, said he expects cent last month and processed food skins and leather goods continued to retail food prices during the first costs were up 0.2 per cent. -

Xavier Gold Rush (5-3) Date Day Opponent Site Time Xavier Gold Rush Vs
Today’s Game: 2013-14 XU Schedule Xavier Gold Rush (5-3) Date Day Opponent Site Time Xavier Gold Rush vs. William Carey Crusaders (4-0) Nov. 1 Fri. CARVER HOME W, 91-67 No. Name Pos. Ht. Yr. Hometown Tuesday, December 3, 2013, 7 p.m. Nov. 6 Wed. LSU (1) Away 45-80 0 Sydney Coleman F 6-7 Jr. Meridian, Miss. Men’s Basketball Convocation Center, New Orleans, La. Nov. 9 Sat. ALBANY STATE HOME W, 71-68 DH 2 Anthony Goode G 6-0 Jr. Baltimore, Md. Nov. 11 Mon. Mobile DH Away W, 88-72 Notable: First of two XU home games in three days . Matchup of Nov. 14 Thu. WILEY HOME W, 86-73 3 Chaz Sharp G 6-3 Jr. Baltimore, Md. ranked NAIA Division I teams — XU is 19th, and William Carey is 10th . Nov. 19 Tue. LOYOLA HOME L, 70-74 4 RJ Daniels G/F 6-4 So. New Orleans, La. Nov. 23 Sat. TEXAS COLLEGE (2) HOME W, 83-47 11th-year XU head coach Dannton Jackson is 231-101 and needs four DH 5 Gary Smith G 6-1 So. Sugar Land, Texas victories to set a Gold Rush record for career victories. He would surpass his Nov. 26 Tue. Wiley Away L, 57-66 10 Wesley Pluviose-Philip F 6-7 Fr. Albany, N.Y. Nov. 30 Sat. LeMoyne-Owen Away L, 62-63 predecessor, Dale Valdery, who was 234-136 from 1990-2002 . XU has won 34 11 Lucas Martin-Julien G 6-2 Fr. Reserve, La. -
The NCAA News
Official Publication of the National Collegiate Athletic Association January 25,1989, Volume 26 Number 4 Some top coaches say limits on TV games vital to attendance Several prominent NCAA foot- I982 figure. “The solution is probably to cut ball coaches cite overexposure on A summary of 1988 football at- down the number of games on tele- television as the major cause of tendance was published in the Jan- vision. How you do that is a good declining attendance for majorcol- uary 4 issue of The NCAA News. question when everybody is fighting lege football in 1987; and while they Division 1-A attendance was for the almighty dollar. Too many advocate some system for control- down in both total and per-game schools are stuggling financially, ling the number of games on televi- average in 1988, which is only the even schools like ours that sell out. sion, none believes that a return to second time that has occurred since “The solution is to go back to the an NCAA t&vision plan is likely to attendance figures have been com- old-fashioned way. If you’re going occur. piled. to watch the ball game, you’ve got According to the NCAA Statis- And that has University of Mich- to pay to get in,” Cooper said. tics Service, attendance at all college igan athletics director and head Mike Archer of Louisiana State football games declined almost football coach ho Schembechler University advocates more selcctiv- 900,000 during the 1988 season, worried. ity. marking the second decline in the He said, “You’re talking about a “1 don’t know what the solution four seasons since the U.S. -
2013-14 Panini Prestige HITS Checklist Basketball
2013-14 Panini Prestige HITS Checklist Basketball 76ers Player Set # Team Seq # Andrew Bynum Frequent Flyer Autographs 22 76ers 49 Andrew Bynum Hoopla Autographs 38 76ers 25 Andrew Bynum Iconic Autographs 37 76ers 25 Bobby Jones Old School Signatures 50 76ers 99 Derrick Coleman Bonus Shots Autographs 52 76ers - Derrick Coleman Bonus Shots Blue Autographs 52 76ers 99 Derrick Coleman Bonus Shots Gold Autographs 52 76ers 10 Derrick Coleman Bonus Shots Green Autographs 52 76ers 5 Derrick Coleman Bonus Shots Platinum Autographs 52 76ers 1 Derrick Coleman Bonus Shots Red Autographs 52 76ers 25 Dikembe Mutombo Bonus Shots Autographs 81 76ers - Dikembe Mutombo Bonus Shots Blue Autographs 81 76ers 49 Dikembe Mutombo Bonus Shots Gold Autographs 81 76ers 10 Dikembe Mutombo Bonus Shots Green Autographs 81 76ers 5 Dikembe Mutombo Bonus Shots Platinum Autographs 81 76ers 1 Dikembe Mutombo Bonus Shots Red Autographs 81 76ers 25 Dolph Schayes Old School Signatures 52 76ers 10 Evan Turner Bonus Shots Materials 73 76ers - Evan Turner Bonus Shots Prime Materials 73 76ers 25 Evan Turner True Colors Materials 63 76ers - Evan Turner True Colors Prime Materials 63 76ers 25 George McGinnis Old School Signatures 17 76ers 99 Hal Greer Old School Signatures 19 76ers 50 Henry Bibby Old School Signatures 47 76ers 99 Jason Richardson Bonus Shots Materials 75 76ers - Jason Richardson Bonus Shots Prime Materials 75 76ers 25 Jason Richardson True Colors Materials 28 76ers - Jason Richardson True Colors Prime Materials 28 76ers 25 Lavoy Allen True Colors Materials 70 -

INSIDE the INSIDE LOOK at Kortemeier SPORTS EVENTS NBA FINALS Inside the Daytona 500
INSIDE THE INSIDE LOOK AT Kortemeier SPORTS EVENTS NBA FINALS Inside the Daytona 500 Inside the NBA Finals INSIDE THE NBA FINALS Inside the Olympics Inside the Super Bowl Inside the World Cup Inside the World Series THE CHILD’S WORLD ® BY TODD KORTEMEIER MOMENTUM Page intentionally blank INSIDE THE NBA FINALS BY TODD KORTEMEIER Published by The Child’s World® 1980 Lookout Drive • Mankato, MN 56003-1705 800-599-READ • www.childsworld.com Acknowledgments The Child’s World®: Mary Berendes, Publishing Director Red Line Editorial: Design, editorial direction, and production Photographs ©: Aaron M. Sprecher/AP Images, cover, 1; Icon Sports Media/Icon Sportswire, 5; Bettmann/Corbis, 6; Mark J. Terrill/AP Images, 9; Jack Smith/AP Images, 10; ZumaPress/Icon Sportswire, 12; San Antonio Express-News/ZumaPress/Icon Sportswire, 14; Kevin Reece/Icon Sportswire, 16; Icon Sportswire, 19; Tom DiPace/AP Images, 20, 24; Lynee Sladky/AP Images, 23; Sue Ogrocki/AP Images, 26, 29 Copyright © 2016 by The Child’s World® All rights reserved. No part of this book may be reproduced or utilized in any form or by any means without written permission from the publisher. ISBN 9781634074360 LCCN 2015946278 Printed in the United States of America Mankato, MN December, 2015 PA02283 ABOUT THE AUTHOR Todd Kortemeier is a writer and journalist from Minneapolis. He is a graduate of the University of Minnesota’s School of Journalism & Mass Communication. TABLE OF CONTENTS Fast Facts ...................................................4 Chapter 1 A Player’s Perspective: THE -

2015-16 Excalibur Basketball Team HITS Checklist
2015-16 Excalibur Basketball Team HITS Checklist Print Player Set Card # Team Run Allen Iverson Kaboom (Non-Hit) 21 76ers Allen Iverson Regal Endorsements 25 76ers 35 Dolph Schayes Regal Endorsements 18 76ers 277 Doug Collins Old School Swatches 22 76ers 99 Jahlil Okafor Head to Toe Signatures 4 76ers 75 Jahlil Okafor Kaboom (Non-Hit) 19 76ers Jahlil Okafor Knight School Jerseys 5 76ers Jahlil Okafor Knight School Jerseys Prime 5 76ers 10 Jahlil Okafor Rookie Rampage Jersey Autographs 3 76ers Jahlil Okafor Rookie Rampage Jersey Autographs Prime 3 76ers 10 Jahlil Okafor Rookie Rampage Jumbo Jersey Autographs 25 76ers Jahlil Okafor Rookie Rampage Jumbo Jersey Autographs Prime 25 76ers 25 Jahlil Okafor Rookie Rampage Jumbo Jerseys 24 76ers 49 Jahlil Okafor Rookie Rampage Jumbo Jerseys Prime 24 76ers 1 Jahlil Okafor Treasured Ink 24 76ers 75 Jerry Stackhouse Head to Toe Swatches 2 76ers 75 Julius Erving Regal Endorsements 27 76ers 32 Nerlens Noel Memorable Memorabilia 1 76ers Richaun Holmes Head to Toe Signatures 17 76ers 75 Richaun Holmes Knight School Jerseys 11 76ers Richaun Holmes Knight School Jerseys Prime 11 76ers 25 Richaun Holmes Rookie Rampage Jersey Autographs 30 76ers Richaun Holmes Rookie Rampage Jersey Autographs Prime 30 76ers 25 Richaun Holmes Rookie Rampage Jumbo Jersey Autographs 20 76ers Richaun Holmes Rookie Rampage Jumbo Jersey Autographs Prime 20 76ers 25 Richaun Holmes Rookie Rampage Jumbo Jerseys 12 76ers 49 Richaun Holmes Rookie Rampage Jumbo Jerseys Prime 12 76ers 25 Robert Covington Treasured Ink 32 76ers 299 T.J. -

Dccbanics & Formers Etanh
c SAT. JAMUARV 31.19W. TYI C wtf" W'""l TIILETIC In w Defending champion North State Saturday night in a pair of road games last week highlight a 10-ga- card in the 80-7- 8 Carolina Carolina A&T and Morgan State Greensboro, at . the Coliseum, losing to Mercer, in an MEAC this week. North are the leaders in the Mid-Easte- rn 91-7- 9. Overall, the Aggies, are overtime Monday night in Central will be the busiest team Athletic Conference 11-- 2 having lost to arch-riv- Macon,; Ga.. and dropping a in the league this week with four race Winston-Sale- m 91-7- 9 on three (MEAC) basketball as the State Friday conference setback to games tap including ? '4 62-5- members of the seven-tea- m night, A&T The league games. The Eagles played , By HERMAN MATOEWS Saturday night conference head into the final Bulldogs are 2 against MEAC S. C. State Monday night, and Morgan State has a clean The National Basketball four weeks of their schedules teams and 9-- 4 overall. will be playing three straight Association's regular season is almost 3-- conference slate at 0. The NCCU at the halfway point. Only have I and seedings in the upcoming road games. Tuesday recently noticed the new theme Bears to a 74-5- 0 North Carolina Central did romped win b or Sth annual MEAC Basketball travels to Gardner-Web- and hits song, tune, whatever, that is being used in conjunction with its over Delaware State not a conference will Thursday play game last for weekend noA) televised games. -

Thunder Media Guide 2016-17 WEB PDF.Pdf
TABLE OF CONTENTS GENERAL INFORMATION All-Time Coaching Records .....................................................................119 General Information .....................................................................................4 Opening Night ..........................................................................................120 All-Time Opening-Night Starting Lineups ................................................121 THUNDER OWNERSHIP GROUP High-Low Scoring Games/Win-Loss Streaks ..........................................122 Clayton I. Bennett ........................................................................................5 All-Time Winning-Losing Streaks/Win-Loss Margins ...............................123 Board of Directors ........................................................................................6 Overtime Results .....................................................................................124 Team Records .........................................................................................126 PLAYERS Opponent Team Records ........................................................................127 Photo Roster ..............................................................................................10 Individual Records ...................................................................................128 Roster ........................................................................................................11 Opponent Individual Records ..................................................................129 -

2020-21 Donruss Basketball Checklist
2020/21 Donruss Basketball Checklist - Hobby Player Set Card # Team Print Run Allen Iverson Relic - Jersey Kings 54 76ers Allen Iverson Relic - Jersey Series 86 76ers Archie Clark Auto - Signature Series 50 76ers Ben Simmons Relic - Jersey Kings 9 76ers Ben Simmons Relic - Jersey Series 1 76ers Ben Simmons Relic - Jersey Series Prime 1 76ers 10 Ben Simmons Relic - Jerseys Kings Prime 9 76ers 10 Matisse Thybulle Relic - Jersey Series 95 76ers Matisse Thybulle Relic - Jersey Series Prime 95 76ers 10 Moses Malone Relic - Jersey Series 59 76ers Tobias Harris Relic - Jersey Series 6 76ers Tobias Harris Relic - Jersey Series Prime 6 76ers 10 Tyrese Maxey Auto - Rated Rookies Signatures + Parallels 211 76ers Tyrese Maxey Auto - Signature Series 84 76ers Tyrese Maxey Relic - Rookie Jersey Kings + Prime Parallel 6 76ers ?? + 25 Al Horford Base 170 76ers Allen Iverson Insert - Retro Series 15 76ers Ben Simmons Base 176 76ers Ben Simmons Insert - Complete Players 7 76ers Ben Simmons Insert - Craftsmen 11 76ers Ben Simmons Insert - Crunch Time 7 76ers Ben Simmons Insert - Fantasy Stars 4 76ers Ben Simmons Insert - Net Marvels 5 76ers Darryl Dawkins Insert - Retro Series 28 76ers Joel Embiid Base 71 76ers Joel Embiid Insert - Complete Players 2 76ers Joel Embiid Insert - Craftsmen 7 76ers Joel Embiid Insert - Crunch Time 6 76ers Joel Embiid Insert - Franchise Features 23 76ers Joel Embiid Insert - Net Marvels 13 76ers Joel Embiid Insert - Power in the Paint 5 76ers Josh Richardson Base 100 76ers Julius Erving Insert - Zero Gravity 9 76ers Matisse