DOCSLIB.ORG

M2-Branes Ending on M5-Branes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
M2-Branes Ending on M5-Branes M2-branes ending on M5-branes Vasilis Niarchos Crete Center for Theoretical Physics, University of Crete 7th Crete Regional Meeting on String Theory, 27/06/2013 based on recent work with K. Siampos 1302.0854, ``The black M2-M5 ring intersection spins’‘ Proceedings Corfu Summer School, 2012 1206.2935, ``Entropy of the self-dual string soliton’’, JHEP 1207 (2012) 134 1205.1535, ``M2-M5 blackfold funnels’’, JHEP 1206 (2012) 175 and older work with R. Emparan, T. Harmark and N. A. Obers ➣ blackfold theory 1106.4428, ``Blackfolds in Supergravity and String Theory’’, JHEP 1108 (2011) 154 0912.2352, ``New Horizons for Black Holes and Branes’’, JHEP 1004 (2010) 046 0910.1601, ``Essentials of Blackfold Dynamics’’, JHEP 1003 (2010) 063 0902.0427, ``World-Volume Effective Theory for Higher-Dimensional Black Holes’’, PRL 102 (2009)191301 0708.2181, ``The Phase Structure of Higher-Dimensional Black Rings and Black Holes’‘ + M.J. Rodriguez JHEP 0710 (2007) 110 2 Important lessons about the fundamentals of string/M-theory (and QFT) are obtained by studying the low-energy theories on D-branes and M-branes. Most notably in M-theory, recent progress has clarified the low-energy QFT on N M2-brane and the N3/2 dof that it exhibits. Bagger-Lambert ’06, Gustavsson ’07, ABJM ’08 Drukker-Marino-Putrov ’10 Our understanding of the M5-brane theory is more rudimentary, but efforts to identify analogous properties, e.g. the N3 scaling of the massless dof, is underway. Douglas ’10 Lambert,Papageorgakis,Schmidt-Sommerfeld ’10 Hosomichi-Seong-Terashima ’12 Kim-Kim ’12 Kallen-Minahan-Nedelin-Zabzine ’12 ... 3 It is believed that the M5 theory is a theory of strings. Townsend ’95, Strominger M2-branes can end on M5-branes ’95, Becker-Becker ’96 ... just like F-strings can end on D-branes in string theory. The above intersection is 1/4-BPS (preserves 8 supercharges). 4 The IR dynamics is controlled by a (1+1)-dim (4,4) SCFT that lives in the intersection. We would like to identify this theory, or key features of this theory e.g. how does the central charge of this CFT scale with N2 , N5 ? Technically, we can approach this question in two different ways: • from a microscopic analysis of the M5/M2 brane physics • from a supergravity analysis of the corresponding black brane intersection (e.g. near-extremal black brane thermodynamics gives 3 2 for M2-branes S N 2 T ⇠ for M5-branes S N 3 T 5 ) e.g. Klebanov-Tseytlin ’96 ⇠ 5 Both approaches are technically complicated. I will describe work in the SUGRA approach. 6 M5 point of view: the Howe-Lambert-West solution Descriptions of the intersection are possible either from the M2 or M5 brane point of view. I will not say much about the M2 point of view, as it will be less relevant for the approach of this talk. Basu-Harvey ’04, (ABJM model with boundary conditions...) Berman et al. ’06, ’09 ... From the M5 point of view the string intersection appears as a solitonic solution of the M5 brane worldvolume theory. 7 Howe, Sezgin, West, Bandos, Lechner, Nurmagambetov, Pasti, Sorokin, Tonin, Aganagic, Park, Poperscu, Schwarz ’96, ’97 The Howe-Lambert-West solution: N5=1, N2>0. The abelian worldvolume theory on a single M5 brane is known. It is a theory of a self-dual 3-form field strength and 5 transverse scalars (plus their fermion partners). Key point: this theory is the leading term in a long-wavelength derivative expansion (analogous to the DBI theory for D-branes). 8 Howe-Lambert-West ’97 The 1/4-BPS self-dual string soliton solution Generalizations (M-theory analog of BIon solution) Gauntlett-Lambert-West ’98 Callan-Maldacena ’97 x6 = z 1 2Qsd 6 x direction suppressed z(σ)= ,z:= x 3 σ2 S H = H = dz σ (3) ⇤6 (3) ⇤4 3 An S spike describes N2 M2-branes ending on N5=1 M5-branes. 9 The solution (and the associated derivative expansion) breaks down at some radius, but a `miracle’ happens: at the tip of the spike one recovers the tension of the orthogonal M2 branes. The leading order solution works much better than naively expected. We will re-encounter and extend this feature below. 10 The non-abelian M5-brane worldvolume theory remains a mostly open subject. Lambert,Papageorgakis ’10 Saemann-Wolf ’11, ’12 Ho-Huang-Matsuo ’11 Bonetti-Grimm-Hohenegger ’12 Samtleben-Sezgin-Wimmer-Wulff ’11, ’12 Chu-Ko ’12 ... This obstructs a similar analysis at generic N2, N5 , but recent progress has been possible. Chu-Ko-Vanichchapongjaroen ’12 Chu-Vanichchapongjaroen ’13 Managed to reproduce one of our supergravity predictions... 11 Known supergravity solutions Supergravity allows us to examine the system in the limit N2, N5 >>1. Brane intersections in supergravity is a subject with a long history and impressive achievements. Nevertheless, in many cases it is technically challenging to find explicit solutions that describe fully localized intersections. ☞ The Einstein equations imply complicated systems of PDEs. The challenge is greater as we reduce the amount of supersymmetry, or if we have no supersymmetry at all, e.g. for non-extremal solutions. 12 In the case of the 1/4-BPS orthogonal M2-M5 intersection we are looking for a solution with SO(1,1) x SO(4) x SO(4) symmetry. A partially localized solution with metric element 2 1/3 2/3 1 2 1 2 1 2 2 5 2 ds = H H (H H )− ( dt +(dx ) )+H− ((dx ) + ...+(dx ) )+ 2 5 2 5 − 5 h 1 6 2 7 2 10 2 H− (dx ) +(dx ) + +(dx ) , 2 ··· i 2 H =0, H 2 + 2 H =0 r(789(10)) 5 5r(2345) r(789(10)) 2 ⇣ ⌘ Duff-Ferrara-Khuri-Rahmfeld ’95 is known (delocalized along the 6-direction). Tseytlin ’96, Gauntlett ’97 Youm ’99, Smith ’02 13 Recent progress towards a fully localized solution ☞ Lunin: 0704.3442 (near-horizon), 0706.3396 (asymptotically flat) derives the appropriate PDEs, solutions are not explicit ☞ D’Hoker-Estes-Gutperle-Krym (near-horizon) 0810.1484, 0806.0605, 0810.4647, 0906.0596 & follow-up: Estes-Feldman-Krym 1209.1845, Berdichevsky-Dahan 1304.4389 explicit families of solutions, but so far unclear which solution describes the orthogonal M2-M5,... 14 I will describe a different treatment of the fully localized solution in SUGRA that • works within a long-wavelength expansion scheme (and is thus technically & conceptually closer to the non-gravitational M5 worldvolume description) • gives immediate intuitive information, and • extends easily to more complicated (less symmetric) configurations that are well beyond the reach of current exact solution generating techniques. analogous description of BIon (F1-D3) solution: Grignani, Harmark, Marini, Obers, Orselli ’10,’11 15 Part of a more general still-developing programme in (super)gravity to: ☞ systematically capture the dynamics of (black) brane solutions with long- wavelength expansion schemes around exact solutions ☞ develop the gravitational analog of DBI-theory for supergravity solutions 16 Blackfold theory basics Emparan, Harmark, VN, Obers Blackfolds provide a general effective (long-wavelength) worldvolume description of black brane dynamics They describe how a black p-brane fluctuates, spins and bends Local patch of Lorentz transformed black p-brane r0 flat black p-brane a thin curved blackfold 17 The fluid/gravity correspondence illustrates nicely the idea. Bhattacharyya-Hubeny- • a spin-off of the AdS/CFT correspondence Minwalla-Rangamani ’07,... • it describes temperature and velocity fluctuations of AdS black branes 1 L2 in the long-wavelength approximation λ AdS T ⇠ r0 in terms of a relativistic conformal fluid. T µ⌫ =0 rµ • the fluid lives on a time-like surface in the asymptotic region of the black hole spacetime (AdS boundary) • there is a constructive perturbative procedure that maps uniquely the solutions of the fluid equations to regular bulk spacetimes 18 Blackfolds add co-dimension to the fluid-gravity correspondence ➠ a mix of fluid dynamics + `DBI’. Long-wavelength fluctuations of a black brane are captured by an effective hydrodynamic theory that describes a fluid on an dynamical worldvolume. The effective degrees of freedom are the slowly-varying temperature, fluid velocity, worldvolume bending scalars, etc. The equations of motion of the effective degrees of freedom are conservation equations for the stress-energy tensor, charge currents... 19 matched asymptotic expansions Outstanding issues Equations of Perturbative expansion of Effective Hydrodynamic Theory (super)gravity equations ☞ Effective Hydro theory has been constructed only at few leading orders. Emparan-Harmark-VN-Rodriguez-Obers ’07 Camps, Emparan ’12 ☞ In progress: effective hydro theory at all orders, general map between hydro solutions and regular bulk spacetimes. We will focus on the leading order of this expansion scheme. 0th order blackfold solution ➠ 1st order thermodynamics 20 M2-M5 blackfold funnels We want to describe a spiky deformation of the planar M5 black brane (with dissolved M2 brane charge) Izquierdo-Lambert- Papadopoulos-Townsend ’95 ➠ how the planar black M2-M5 bound state deforms Russo-Tseytlin ’96 1 F4 = dC3 + D− ?dC6 21 The parameters of the planar M2-M5 bound state are promoted to slowly- varying functions of the effective 5-brane worldvolume coordinates Effective degrees of freedom a a a a a a ˆ r0(ˆσ ) ,↵(ˆσ ) ,✓(ˆσ ) ,u(ˆσ ) ,X?(ˆσ ) , V(3) unit 3-volume form local temperature M2, M5 charges local transverse boosts scalars controls embedding of M2 charge in 5-brane wv 22 Leading order blackfold equations i Kab : extrinsic curvature `hydrodynamic’ part tensor `DBI’ part intrinsic equations extrinsic equations i ab ab Kab T =0 DaT =0 d J =0,J= Vˆ ⇤ 3 3 Q2 (3) d J =0,J= Vˆ ⇤ 6 6 Q5 (6) local stress-energy tensor, constitutive relations,..
Load more

Recommended publications
  • From Vibrating Strings to a Unified Theory of All Interactions
    Barton Zwiebach From Vibrating Strings to a Unified Theory of All Interactions or the last twenty years, physicists have investigated F String Theory rather vigorously. The theory has revealed an unusual depth. As a result, despite much progress in our under- standing of its remarkable properties, basic features of the theory remain a mystery. This extended period of activity is, in fact, the second period of activity in string theory. When it was first discov- ered in the late 1960s, string theory attempted to describe strongly interacting particles. Along came Quantum Chromodynamics— a theoryof quarks and gluons—and despite their early promise, strings faded away. This time string theory is a credible candidate for a theoryof all interactions—a unified theoryof all forces and matter. The greatest complication that frustrated the search for such a unified theorywas the incompatibility between two pillars of twen- tieth century physics: Einstein’s General Theoryof Relativity and the principles of Quantum Mechanics. String theory appears to be 30 ) zwiebach mit physics annual 2004 the long-sought quantum mechani- cal theory of gravity and other interactions. It is almost certain that string theory is a consistent theory. It is less certain that it describes our real world. Nevertheless, intense work has demonstrated that string theory incorporates many features of the physical universe. It is reasonable to be very optimistic about the prospects of string theory. Perhaps one of the most impressive features of string theory is the appearance of gravity as one of the fluctuation modes of a closed string. Although it was not discov- ered exactly in this way, we can describe a logical path that leads to the discovery of gravity in string theory.
    [Show full text]
  • The Fuzzball Proposal for Black Holes: an Elementary Review
    hep-th/0502050 The fuzzball proposal for black holes: an elementary review1 Samir D. Mathur Department of Physics, The Ohio State University, Columbus, OH 43210, USA [email protected] Abstract We give an elementary review of black holes in string theory. We discuss BPS holes, the microscopic computation of entropy and the ‘fuzzball’ picture of the arXiv:hep-th/0502050v1 3 Feb 2005 black hole interior suggested by microstates of the 2-charge system. 1Lecture given at the RTN workshop ‘The quantum structure of space-time and the geometric nature of fundamental interactions’, in Crete, Greece (September 2004). 1 Introduction The quantum theory of black holes presents many paradoxes. It is vital to ask how these paradoxes are to be resolved, for the answers will likely lead to deep changes in our understanding of quantum gravity, spacetime and matter. Bekenstein [1] argued that black holes should be attributed an entropy A S = (1.1) Bek 4G where A is the area of the horizon and G is the Newton constant of gravitation. (We have chosen units to set c = ~ = 1.) This entropy must be attributed to the hole if we are to prevent a violation of the second law of thermodynamics. We can throw a box of gas with entropy ∆S into a black hole, and see it vanish into the central singularity. This would seem to decrease the entropy of the Universe, but we note that the area of the horizon increases as a result of the energy added by the box. It turns out that if we assign (1.1) as the entropy of the hole then the total entropy is nondecreasing dS dS Bek + matter 0 (1.2) dt dt ≥ This would seem to be a good resolution of the entropy problem, but it leads to another problem.
    [Show full text]
  • String Theory for Pedestrians
    String Theory for Pedestrians – CERN, Jan 29-31, 2007 – B. Zwiebach, MIT This series of 3 lecture series will cover the following topics 1. Introduction. The classical theory of strings. Application: physics of cosmic strings. 2. Quantum string theory. Applications: i) Systematics of hadronic spectra ii) Quark-antiquark potential (lattice simulations) iii) AdS/CFT: the quark-gluon plasma. 3. String models of particle physics. The string theory landscape. Alternatives: Loop quantum gravity? Formulations of string theory. 1 Introduction For the last twenty years physicists have investigated String Theory rather vigorously. Despite much progress, the basic features of the theory remain a mystery. In the late 1960s, string theory attempted to describe strongly interacting particles. Along came Quantum Chromodynamics (QCD)– a theory of quarks and gluons – and despite their early promise, strings faded away. This time string theory is a credible candidate for a theory of all interactions – a unified theory of all forces and matter. Additionally, • Through the AdS/CFT correspondence, it is a valuable tool for the study of theories like QCD. • It has helped understand the origin of the Bekenstein-Hawking entropy of black holes. • Finally, it has inspired many of the scenarios for physics Beyond the Standard Model of Particle physics. 2 Greatest problem of twentieth century physics: the incompatibility of Einstein’s General Relativity and the principles of Quantum Mechanics. String theory appears to be the long-sought quantum mechanical theory of gravity and other interactions. It is almost certain that string theory is a consistent theory. It is less certain that it describes our real world.
    [Show full text]
  • Three Duality Symmetries Between Photons and Cosmic String Loops, and Macro and Micro Black Holes
    Symmetry 2015, 7, 2134-2149; doi:10.3390/sym7042134 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article Three Duality Symmetries between Photons and Cosmic String Loops, and Macro and Micro Black Holes David Jou 1;2;*, Michele Sciacca 1;3;4;* and Maria Stella Mongiovì 4;5 1 Departament de Física, Universitat Autònoma de Barcelona, Bellaterra 08193, Spain 2 Institut d’Estudis Catalans, Carme 47, Barcelona 08001, Spain 3 Dipartimento di Scienze Agrarie e Forestali, Università di Palermo, Viale delle Scienze, Palermo 90128, Italy 4 Istituto Nazionale di Alta Matematica, Roma 00185 , Italy 5 Dipartimento di Ingegneria Chimica, Gestionale, Informatica, Meccanica (DICGIM), Università di Palermo, Viale delle Scienze, Palermo 90128, Italy; E-Mail: [email protected] * Authors to whom correspondence should be addressed; E-Mails: [email protected] (D.J.); [email protected] (M.S.); Tel.: +34-93-581-1658 (D.J.); +39-091-23897084 (M.S.). Academic Editor: Sergei Odintsov Received: 22 September 2015 / Accepted: 9 November 2015 / Published: 17 November 2015 Abstract: We present a review of two thermal duality symmetries between two different kinds of systems: photons and cosmic string loops, and macro black holes and micro black holes, respectively. It also follows a third joint duality symmetry amongst them through thermal equilibrium and stability between macro black holes and photon gas, and micro black holes and string loop gas, respectively. The possible cosmological consequences of these symmetries are discussed. Keywords: photons; cosmic string loops; black holes thermodynamics; duality symmetry 1. Introduction Thermal duality relates high-energy and low-energy states of corresponding dual systems in such a way that the thermal properties of a state of one of them at some temperature T are related to the properties of a state of the other system at temperature 1=T [1–6].
    [Show full text]
  • Chapter 9: the 'Emergence' of Spacetime in String Theory
    Chapter 9: The `emergence' of spacetime in string theory Nick Huggett and Christian W¨uthrich∗ May 21, 2020 Contents 1 Deriving general relativity 2 2 Whence spacetime? 9 3 Whence where? 12 3.1 The worldsheet interpretation . 13 3.2 T-duality and scattering . 14 3.3 Scattering and local topology . 18 4 Whence the metric? 20 4.1 `Background independence' . 21 4.2 Is there a Minkowski background? . 24 4.3 Why split the full metric? . 27 4.4 T-duality . 29 5 Quantum field theoretic considerations 29 5.1 The graviton concept . 30 5.2 Graviton coherent states . 32 5.3 GR from QFT . 34 ∗This is a chapter of the planned monograph Out of Nowhere: The Emergence of Spacetime in Quantum Theories of Gravity, co-authored by Nick Huggett and Christian W¨uthrich and under contract with Oxford University Press. More information at www.beyondspacetime.net. The primary author of this chapter is Nick Huggett ([email protected]). This work was sup- ported financially by the ACLS and the John Templeton Foundation (the views expressed are those of the authors not necessarily those of the sponsors). We want to thank Tushar Menon and James Read for exceptionally careful comments on a draft this chapter. We are also grateful to Niels Linnemann for some helpful feedback. 1 6 Conclusions 35 This chapter builds on the results of the previous two to investigate the extent to which spacetime might be said to `emerge' in perturbative string the- ory. Our starting point is the string theoretic derivation of general relativity explained in depth in the previous chapter, and reviewed in x1 below (so that the philosophical conclusions of this chapter can be understood by those who are less concerned with formal detail, and so skip the previous one).
    [Show full text]
  • Type II and Heterotic One Loop String Effective Actions in Four Dimensions
    Type II and heterotic one loop string effective actions in four dimensions Filipe Moura Security and Quantum Information Group - Instituto de Telecomunica¸c˜oes Instituto Superior T´ecnico, Departamento de Matem´atica Av. Rovisco Pais, 1049-001 Lisboa, Portugal [email protected] Abstract We analyze the reduction to four dimensions of the 4 terms which are part of the ten-dimensional string effective actions, bothR at tree level and one loop. We show that there are two independent combinations of 4 R present, at one loop, in the type IIA four dimensional effective action, which means they both have their origin in M-theory. The d = 4 heterotic effective action also has such terms. This contradicts the common belief that there is only one 4 term in four-dimensional supergravity theories, given by the square of theR Bel-Robinson tensor. In pure = 1 supergravity this new N 4 combination cannot be directly supersymmetrized, but we show that, whenR coupled to a scalar chiral multiplet (violating the U(1) R-symmetry), arXiv:hep-th/0703026v2 12 Jun 2007 it emerges in the action after elimination of the auxiliary fields. Contents 1 Introduction 1 2 String effective actions to order α′3 in d = 10 3 3 String effective actions to order α′3 in d =4 5 3.1 4 terms in d = 4 from d =10....................... 5 R 3.2 Moduli-independent terms in d =4effectiveactions . 8 4 4 terms and d =4 supersymmetry 10 4.1R Someknownresults............................. 10 4.2 4 + 4 in =1matter-coupledsupergravity . 11 W+ W− N 4.3 4 + 4 inextendedsupergravity .
    [Show full text]
  • Physics 250: String Theory and M-Theory
    Physics 250: String Theory and M-Theory Instructor: Petr Hoˇrava Spring 2007, Tue & Thu, 2:10-3:30, 402 Le Conte Hall String theory is one of the most exciting and challenging areas of modern theoretical physics, whose techniques and concepts have implications in diverse fields ranging from pure mathematics, to particle phenomenology, to cosmology, to condensed matter theory. This course will provide a one-semester introduction to string and M-theory, from the basics all the way to the most modern developments. This will be possible because the course will follow an excellent one-volume book that is now being published, [1] K. Becker, M. Becker and J.H. Schwarz, String Theory and M-Theory: A Mod- ern Introduction (Cambridge U. Press, November 2006). Topics covered in the course will follow the chapters of [1]: 1. Introduction; 2. The bosonic string; 3. Conformal field theory and string interactions; 4. Strings with worldsheet supersymmetry; 5. Strings with spacetime supersymmetry; 6. T-duality and D-branes; 7. The heterotic string; 8. M-theory and string duality; 9. String geometry; 10. Flux compactifications; 11. Black holes in string theory; 12. Gauge theory/string theory dualities, AdS/CFT. The prerequisites for the course are: some knowledge of basic quantum field theory (at the level of 230A or at least 229A), some knowledge of basics of general relativity (at the level of 231). Students who are interested in signing for the course but are worried about not satisfying these requirements are encouraged to talk to the instructor about the possibility of waiving the prerequisites.
    [Show full text]
  • Confinement in Yang{Mills: Elements of a Big Picture
    October 2008 UMN-TH-2720/08 , FTPI-MINN-08/38 , SLAC-PUB-13434 Confinement in Yang{Mills: Elements of a Big Picture M. Shifmana;b and Mithat Unsal• c;d a William I. Fine Theoretical Physics Institute, University of Minnesota, Minneapolis, MN 55455, USA b Laboratoire de Physique Th´eorique1 Universit´ede Paris-Sud XI Bˆatiment 210, F-91405 Orsay C´edex,FRANCE c SLAC, Stanford University, Menlo Park, CA 94025, USA d Physics Department, Stanford University, Stanford, CA,94305, USA Abstract This is a combined and slightly expanded version of talks deliv- ered at 14th International QCD Conference “QCD 08,” 7-12th July 2008, Montpellier, France, the International Conference “Quark Con- finement and the Hadron Spectrum,” Mainz, Germany, September 1-6, 2008 (Confinement 08), and the International Conference “Approaches to Quantum Chromodynamics,” Oberw•olz,Austria, September 7-13, 2008. Work supported in part by US Department of Energy contract DE-AC02-76SF00515 1UniteMixte de Recherche du CNRS, (UMR 8627). 1 Introduction QCD is a non-Abelian gauge theory of strong interactions. It is extremely rich and describes a very wide range of natural phenomena, e.g.: all of nuclear physics; Regge behavior and Regge trajectories; strongly coupled quark-gluon plasma; high-T and high-density phenom- ena; neutron stars; richness of the hadronic world (chiral phenomena, light and heavy quarkonia, glueballs and exotics, exclusive and inclusive processes, interplay between strong and weak interactions, and many other issues). At short distances QCD is weakly coupled, allowing high precision pertur- bative (multi-loop, multi-leg) calculations, however, analytical computations at all energy and momentum scales seem unlikely due to strong coupling nature at large distances.
    [Show full text]
  • Towards String Theory Expectations for Photon Couplings to Axionlike Particles
    PHYSICAL REVIEW D 100, 106010 (2019) Towards string theory expectations for photon couplings to axionlike particles James Halverson, Cody Long, Brent Nelson, and Gustavo Salinas Department of Physics, Northeastern University Boston, Massachusetts 02115-5000, USA (Received 25 September 2019; published 21 November 2019) Axionlike particle (ALP)–photon couplings are modeled in large ensembles of string vacua and random matrix theories. In all cases, the effective coupling increases polynomially in the number of ALPs, of which hundreds or thousands are expected in the string ensembles, many of which are ultralight. The expected −12 −1 −10 −1 value of the couplings gaγγ ≃ 10 GeV − 10 GeV provide viable targets for future x-ray telescopes and axion helioscopes, and in some cases are already in tension with existing data. DOI: 10.1103/PhysRevD.100.106010 I. INTRODUCTION window, we will focus on analyses relevant for experiments that do not require ALP dark matter and only set limits If string theory is the correct theory of quantum gravity, below a fixed mass threshold. one of its vacua must realize the photon of classical For such experiments, the strongest bounds on the electromagnetism. Uncharged spin zero particles must cou- coupling arise at low mass, m ≤ 10−2 eV, where ple to the electromagnetic field strength, since all couplings a results [1] from the axion helioscope CAST require in string theory are determined by vacuum expectationvalues ≤ 7 10−11 −1 (VEVs) of scalar fields. This applies not only to the usual gaγγ × GeV . The CAST result already signifi- μν cantly outperforms projected collider bounds for m ≃ GeV parity even operator FμνF , but also the parity odd operator, a scale ALPs, leading us to focus on the low mass range.
    [Show full text]
  • A String Theory Which Isn't About Strings Arxiv:1708.05707V3 [Hep-Th]
    A String Theory Which Isn't About Strings Kanghoon Lee, a∗ Soo-Jong Rey, by J. A. Rosabal az aFields, Gravity & Strings @ CTPU, Institute for Basic Science, 70 Yuseong-daero 1689-gil, Daejeon 34047, KOREA bSchool of Physics & Astronomy and Center for Theoretical Physics, Seoul National University, 1 Gwanak-ro, Seoul 08862, KOREA Abstract Quantization of closed string proceeds with a suitable choice of worldsheet vacuum. A priori, the vacuum may be chosen independently for left-moving and right-moving sec- tors. We construct ab initio quantized bosonic string theory with left-right asymmetric worldsheet vacuum and explore its consequences and implications. We critically examine the validity of new vacuum and carry out first-quantization using standard operator for- malism. Remarkably, the string spectrum consists only of a finite number of degrees of freedom: string gravity (massless spin-two, Kalb-Ramond and dilaton fields) and two mas- sive spin-two Fierz-Pauli fields. The massive spin-two fields have negative norm, opposite mass-squared, and provides a Lee-Wick type extension of string gravity. We compute two physical observables: tree-level scattering amplitudes and one-loop cosmological constant. Scattering amplitude of four dilatons is shown to be a rational function of kinematic invari- ants, and in D = 26 factorizes into contributions of massless spin-two and a pair of massive spin-two fields. The string one loop partition function is shown to perfectly agree with one loop Feynman diagram of string gravity and two massive spin-two fields. In particular, it does not exhibit modular invariance. We critically compare our construction with recent studies and contrast differences.
    [Show full text]
  • Arxiv:2010.07320V3 [Hep-Ph] 15 Jun 2021 Yecag Portal
    Preprint typeset in JHEP style - HYPER VERSION UWThPh 2020-15 CCTP-2020-7 ITCP-IPP-2020/7 String (gravi)photons, “dark brane photons”, holography and the hypercharge portal P. Anastasopoulos1,∗ M. Bianchi2,† D. Consoli1,‡ E. Kiritsis3 1 Mathematical Physics Group, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria 2 Dipartimento di Fisica, Universit`adi Roma “Tor Vergata” & I.N.F.N. Sezione di Roma “Tor Vergata”, Via della Ricerca Scientifica, 00133 Roma, Italy 3 Crete Center for Theoretical Physics, Institute for Theoretical and Computational Physics, Department of Physics, University of Crete, 70013, Heraklion, Greece and Universite de Paris, CNRS, Astroparticule et Cosmologie, F-75006 Paris, France Abstract: The mixing of graviphotons and dark brane photons to the Standard Model hypercharge is analyzed in full generality, in weakly-coupled string theory. Both the direct mixing as well as effective terms that provide mixing after inclusion of arXiv:2010.07320v3 [hep-ph] 15 Jun 2021 SM corrections are estimated to lowest order. The results are compared with Effective Field Theory (EFT) couplings, originating in a hidden large-N theory coupled to the SM where the dark photons are composite. The string theory mixing terms are typically subleading compared with the generic EFT couplings. The case where the hidden theory is a holographic theory is also analyzed, providing also suppressed mixing terms to the SM hypercharge. Keywords: Emergent photon, dark photon, graviphoton, holography, mixing, hypercharge portal. ∗[email protected] †[email protected] ‡[email protected] Contents 1. Introduction 2 1.1 The field theory setup 5 1.2 Results and outlook 7 2.
    [Show full text]
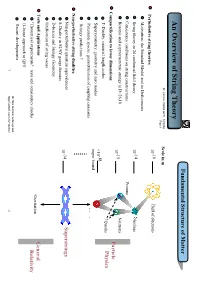
  • String-Theory
    CERN Fundamental Structure of Matter An Overview of String Theory W. Lerche, CERN AcTr, 12/2002 Scale in m Part 1 10-10 Hull of electrons Perturbative string theories Motivation: the Standard Model and its Deficiencies String theory as 2d conformal field theory 10-14 Nucleus Consistency conditions on string constructions Protons Bosonic and supersymmetric strings in D=26,10 Neutrons 10-15 Compactification to lower dimensions Particle Quarks Physics T-Duality, minimal length scales <10-18 Supersymmetry, geometry and zero modes exper bound Parameter spaces, geometrization of coupling constants Stringy predictions ? Non-perturbative string dualities Non-perturbative quantum equivalences Superstrings 10-34 S-Duality in SUSY gauge theories D-branes and Stringy Geometry Unification of string vacua Tests and Applications General Gravitation "Theoretical experiments": tests and consistency checks Relativity D-brane approach to QFT Recent developments for files and text write-up see: 1 http://nxth21.cern.ch/~lerche/ 2 Physics of Elementary Particles Deficiencies of the Standard Model Its structure is quite ad hoc: are there deeper principles ? Interactions Carriers elementary ("grand unification" of all matter and forces) (Forces) (Gauge Fields) Matter Fields ca 25 free parameters: determined by what ? Electromagnetism Photon Leptons (eg electrons) weak Interactions W,Z-Bosons massess Higgs VEVs (Radioactivity) gauge couplings Quarks strong Interactions Gauge hierarchy: Gluons (binds Nuclei) There are three why weak scale (100GeV) << Unification
    [Show full text]