Modeling and Simulation of Skid Steered Robot Pioneer-3AT
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
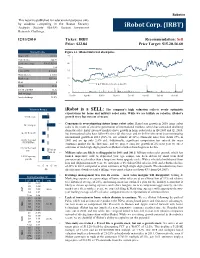
Robotics Irobot Corp. (IRBT)
Robotics This report is published for educational purposes only by students competing in the Boston Security Analysts Society (BSAS) Boston Investment iRobot Corp. (IRBT) Research Challenge. 12/13/2010 Ticker: IRBT Recommendation: Sell Price: $22.84 Price Target: $15.20-16.60 Market Profile Figure 1.1: iRobot historical stock price Shares O/S 25 mm 25 Current price $22.84 52 wk price range $14.45-$23.00 20 Beta 1.86 iRobot 3 mo ADTV 0.14 mm 15 Short interest 2.1 mm Market cap $581mm 10 Debt 0 S & P 500 (benchmarked Jan-09) P/10E 25.2x 5 EV/10 EBITDA 13.5x Instl holdings 57.8% 0 Jan-09 Apr-09 Jul-09 Oct-09 Jan-10 Apr-10 Jul-10 Oct-10 Insider holdings 12.5% Valuation Ranges iRobot is a SELL: The company’s high valuation reflects overly optimistic expectations for home and military robot sales. While we are bullish on robotics, iRobot’s 52 wk range growth story has run out of steam. • Consensus is overestimating future home robot sales: Rapid yoy growth in 2010 home robot Street targets sales is the result of one-time penetration of international markets, which has concealed declining domestic sales. Entry into new markets drove growth in home robot sales in Q4 2009 and Q1 2010, 20-25x P/2011E but international sales have fallen 4% since Q1 this year, and we believe the street is overestimating international growth in 2011 (30% vs. our estimate of 18%). Domestic sales were down 29% in 8-12x Terminal 2009 and are up only 2.5% ytd. -

A National Imperative
TorchbearerTorchbearer NationalNational SecuritySecurity ReportReport A Transformed and Modernized U.S. Army: A National Imperative An AUSA Torchbearer Issue April 2007 April 2007 9 April 2007 A speaker at an AUSA-sponsored Land Warfare forum in January 1992 spoke on the U.S. Army in the post-industrial world and outlined some Army requirements: a family of combat vehicles capable of fi ghting on the ground together at full tempo; Army air vehicles that complement the ground vehicles in a synergistic way, multiplying the capability of ground forces; systems that enable commanders to command and control the force, enhancing a common perception of the battlefi eld; and the ability to sustain the force—not only with mass quantities but with precision. Th e continued operational requirements Soldiers have encountered in the subsequent 15 years have only served to validate those requirements, and it is gratifying to see the Army make steady progress toward satisfying them. Th e strength of the Army results from whole, cohesive units and Soldiers that are fully manned, equipped, trained and ready to conduct full-spectrum operations today—and modernized to meet the challenges of today and tomorrow. Th e Army has adopted a new comprehensive, innovative modernization strategy. Th at strategy provides the best equipment currently available to Soldiers fi ghting the Global War on Terror while simultaneously developing new capabilities essential for future operations. In this latest installment of AUSA’s signature Torchbearer series, we provide an in-depth analysis of the Army’s modernization plan—centered on Future Combat Systems technologies and a holistic, system-of-systems approach—to prepare the Army for success in the complex environment of the 21st century. -

Irobot® Warrior™ X700 a MULTI-MISSION, MODULAR ROBOT with SUPERIOR POWER
iRobot® Warrior™ X700 A MULTI-MISSION, MODULAR ROBOT WITH SUPERIOR POWER The iRobot Warrior is a powerful critical in a variety of missions, FLEX THE ROBOT’S MUSCLES and rugged robot that can carry including explosive ordnance The Warrior is highly configurable • CBRN greater than 150 lb payloads, travel disposal (EOD), reconnaissance, and to meet the demands of real-world • Battlefield Casualty Extraction through rough terrain and climb firefighting.Funded by the Technical situations such as: • Physical Security stairs with heavy loads. The robot’s Support Working Group (TSWG), • Explosive Ordnance Disposal design offers an advanced digital Warrior is currently under develop- • Firefighting • VBIED architecture and an extremely sturdy ment and is expected to become • Surveillance • SWAT platform to support the weight of available for sale in early 2008. • Target Acquisition • Reconnaissance heavy payloads, such as firearms • Weaponized Missions and hoses. The Warrior robot will be • HazMat iRobot Warrior Chassis Capabilities and Specifications Length Software Battery Endurance Deployment 40 inches First robot designed specifically – 9-Pack Sincgars Radio Lithium Rapidly deployable from non- Width for AWARE 2.0 Ion Batteries specialized vehicle 29 - 32.5 inches Navigation – 1.45 - 16 hours depending Mobility on mission profile. (depending on configuration) Leverages odometry waypoint Dual track system for enhanced 1.0 minute change-out for bat- Height navigation via built-in GPS model mobility teries 18 inches (stowed) Supports assisted tele-operated Maintenance behavior: Hardened Electronics Weight Fast pit-stop like plug and play – Obstacle avoidance sensors MIL-STD-461 – Approximately 250 lbs. concept using 3-tiered – Intelligent CG shifting MIL-STD-464 maintenance concept: – Total weight of platform and flipper control and mission payloads: Communications – Field Maintenance 400 lbs. -

Intelligent Robotic Behaviors for Landmine Detection and Marking
Journal of Conventional Weapons Destruction Volume 11 Issue 2 The Journal of Mine Action Article 42 April 2008 Intelligent Robotic Behaviors for Landmine Detection and Marking David Bremmer Idaho National Laboratory David Few Idaho National Laboratory Curtis Nielsen Idaho National Laboratory Miles Walton Idaho National Laboratory Follow this and additional works at: https://commons.lib.jmu.edu/cisr-journal Part of the Defense and Security Studies Commons, Emergency and Disaster Management Commons, Other Public Affairs, Public Policy and Public Administration Commons, and the Peace and Conflict Studies Commons Recommended Citation Bremmer, David; Few, David; Nielsen, Curtis; and Walton, Miles (2008) "Intelligent Robotic Behaviors for Landmine Detection and Marking," Journal of Mine Action : Vol. 11 : Iss. 2 , Article 42. Available at: https://commons.lib.jmu.edu/cisr-journal/vol11/iss2/42 This Article is brought to you for free and open access by the Center for International Stabilization and Recovery at JMU Scholarly Commons. It has been accepted for inclusion in Journal of Conventional Weapons Destruction by an authorized editor of JMU Scholarly Commons. For more information, please contact [email protected]. Bremmer et al.: Intelligent Robotic Behaviors for Landmine Detection and Marking should absorb most of the blast energy.6 Also, During a recent visit to Cornell University, all the expensive sensors and computers are Nobel Peace Prize Co-laureate Rae McGrath had enclosed in a watertight, rugged box, which is the chance to meet with Cornell MineSweeper. being refined to meet military specifications “I really want to congratulate Cornell for allow- Intelligent Robotic Behaviors for Landmine Detection and Marking for explosion proofing. -

Helen Greiner 11 Gage Road Wayland MA 01778 617-669-6665
Helen Greiner Prepared Testimony 11 Gage Road Senate Commerce Committee Wayland MA 01778 The Case for Space: Examining the Value 617-669-6665 October 23, 2009, 2:30PM [email protected] My name is Helen Greiner. I am currently the CEO of a startup company called The Droid Works. I received my Bachelors Degree in Mechanical Engineering and Masters Degree in Electrical and Computer Sciences from the Massachusetts Institute of Technology. Between 1990 to 2008, I cofounded and served as President and later Chairman of iRobot Corporation, a company that went from an apartment based startup to a publicly traded company and is a worldwide leaders in robot product sales and cutting edge robotics research. I currently serve as a trustee for MIT, the Boston Museum of Science, the National Defense Industrial Association, and the Association for Unmanned Vehicle Systems International. I also serve as the elected President of the Robotics Technology Consortium, an industrial and academic consortium of 179 companies including top tier defense contractors, top universities and non profits, and over 120 small businesses – we have members from over 2/3 of the states. In other words, I am an engineer, entrepreneur, and active in representing the robotics industry. My own career and iRobot’s history is inextricably intertwined with NASA. I was an intern at NASA’s Jet Propulsion Laboratory where I worked on manipulators for satellites. This internship provided the opportunity to learn from NASA engineers and the support that I needed to pursue an advanced degree. Upon graduating, I founded iRobot in 1990 with Rod Brooks and Colin Angle, and NASA helped by purchasing robots from us – specifically an 18 degree of freedom walking robot and two portable tracked robots our very first sales. -

SAFER: Search and Find Emergency Rover Zachary Agustin Santa Clara University
Santa Clara University Scholar Commons Mechanical Engineering Senior Theses Engineering Senior Theses 6-8-2016 SAFER: Search and Find Emergency Rover Zachary Agustin Santa Clara University Charles Lewis Santa Clara University Elizabeth McMahon Santa Clara University Cameron Pierce Santa Clara University Pranav Pradhan Santa Clara University See next page for additional authors Follow this and additional works at: https://scholarcommons.scu.edu/mech_senior Part of the Mechanical Engineering Commons Recommended Citation Agustin, Zachary; Lewis, Charles; McMahon, Elizabeth; Pierce, Cameron; Pradhan, Pranav; and Tamshen, Michael, "SAFER: Search and Find Emergency Rover" (2016). Mechanical Engineering Senior Theses. 63. https://scholarcommons.scu.edu/mech_senior/63 This Thesis is brought to you for free and open access by the Engineering Senior Theses at Scholar Commons. It has been accepted for inclusion in Mechanical Engineering Senior Theses by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Author Zachary Agustin, Charles Lewis, Elizabeth McMahon, Cameron Pierce, Pranav Pradhan, and Michael Tamshen This thesis is available at Scholar Commons: https://scholarcommons.scu.edu/mech_senior/63 SAFER: SEARCH AND FIND EMERGENCY ROVER By Zachary Agustin, Charles Lewis, Elizabeth McMahon, Cameron Pierce, Pranav Pradhan, and Michael Tamshen SENIOR DESIGN PROJECT REPORT Submitted to the Department of Mechanical Engineering of SANTA CLARA UNIVERSITY in Partial Fulfillment of the Requirements for the degree of Bachelor of Science in Mechanical Engineering Santa Clara, California Spring 2016 ii SAFER: Search and Find Emergency Rover Zachary Agustin, Charles Lewis, Elizabeth McMahon, Cameron Pierce, Pranav Pradhan, and Michael Tamshen Department of Mechanical Engineering Santa Clara University 2016 Abstract When disaster strikes and causes a structure to collapse, it poses a unique challenge to search and rescue teams as they assess the situation and search for survivors. -

Packbot: a Versatile Platform for Military Robotics
PackBot: A Versatile Platform for Military Robotics Brian Yamauchi iRobot Corporation, 63 South Avenue, Burlington, MA 01803-4903 ABSTRACT The iRobot PackBot is a combat-tested, man-portable UGV that has been deployed in Afghanistan and Iraq. The PackBot is also a versatile platform for mobile robotics research and development that supports a wide range of payloads suitable for many different mission types. In this paper, we describe four R&D projects that developed experimental payloads and software using the PackBot platform. CHARS was a rapid development project to develop a chemical/radiation sensor for the PackBot. We developed the CHARS payload in six weeks and deployed it to Iraq to search for chemical and nuclear weapons. Griffon was a research project to develop a flying PackBot that combined the capabilities of a UGV and a UAV. We developed a Griffon prototype equipped with a steerable parafoil and gasoline- powered motor, and we completed successful flight tests including remote-controlled launch, ascent, cruising, descent, and landing. Valkyrie is an ongoing research and development project to develop a PackBot payload that will assist medics in retrieving casualties from the battlefield. Wayfarer is an applied research project to develop autonomous urban navigation capabilities for the PackBot using laser, stereo vision, GPS, and INS sensors. Keywords: Robotics, UGV, UAV, chemical and radiation sensors, casualty evacuation, autonomous navigation. 1. INTRODUCTION The iRobot PackBot is a rugged, man-portable, all-terrain, all-weather mobile robot that has been combat tested in Afghanistan and Iraq. Soldiers in the 82nd and 101st Airborne Divisions and Special Operations have used PackBots to search Al Qaeda caves in Afghanistan and hunt for chemical and nuclear weapons in Iraq. -

Investigating the Mobility of Unmanned Ground Vehicles
Investigating the Mobility of Unmanned Ground Vehicles S. Odedra, S.D. Prior and M. Karamanoglu Middlesex University, School of Engineering and Information Sciences, Department of Product Design and Engineering, Trent Park Campus, Bramley Road, London, N14 4YZ, U.K. [email protected] Abstract operated, has the hardest job in terms of navigating in its environment. This is because ground conditions Unmanned Vehicles have to be as capable if not more include a number of different obstacles, both positive capable than a human in the same situation, and negative, over a range of different terrain types especially when used by the military to serve as an extension of the soldiers capability on the battlefield. and UGV’s generally have to operate in unknown, All unmanned systems types have obstacles and unstructured environments which include a large encounter difficulties when trying to complete their number of unpredictable and dynamic variables, missions, but none more so than the Unmanned making the seemingly simple task of traversing very Ground Vehicle (UGV). This is because UGV’s have hard; and this was demonstrated at the first DARPA to operate in environments with a large amount of Grand Challenge in 2004 where all the unmanned variables which includes a range of different obstacles, and terrain types; making the simple task systems failed to complete the course due to not of driving from A to B very hard. This highlights the being able to sense and adapt to the environment or fact that a UGV’s capability is predominantly any situational changes [1]. dependant on its mobility and is seen as one of the most important factors in their development, because The Defence and Security Industry is the largest the more capable of traversing over all types of operator of unmanned vehicles and they also invest terrain the vehicle is, then the less likely it will the largest funding towards their research and become stuck and need human assistance. -

Autonomous Weapon Systems: Technical, Military, Legal and Humanitarian Aspects
EXPERT MEETING AUTONOMOUS WEAPON SYSTEMS TECHNICAL, MILITARY, LEGAL AND HUMANITARIAN ASPECTS GENEVA, SWITZERLAND 26 TO 28 MARCH 2014 International Committee of the Red Cross 19, avenue de la Paix 1202 Geneva, Switzerland T +41 22 734 60 01 F +41 22 733 20 57 E-mail: [email protected] www.icrc.org © ICRC, November 2014 AUTONOMOUS WEAPON SYSTEMS: TECHNICAL, MILITARY, LEGAL AND HUMANITARIAN ASPECTS EXPERT MEETING GENEVA, SWITZERLAND 26 to 28 MARCH 2014 Autonomous weapon systems: Technical, military, legal and humanitarian aspects. 2 Expert meeting, Geneva, Switzerland, 26-28 March 2014. CONTENTS Introduction and structure of the report 5 Part I: Summary report by the International Committee of the Red Cross 7 Meeting highlights 7 Background 11 Summary of presentations and discussions 12 Part II: Selected presentations 25 Civilian robotics and developments in autonomous systems 25 – Ludovic Righetti Autonomous weapons and human supervisory control 29 – Noel Sharkey Ethical restraint of lethal autonomous robotic systems: Requirements, 33 research, and implications – Ronald Arkin Research and development of autonomous ‘decision-making’ systems 39 – Darren Ansell Can autonomous weapon systems respect the principles of distinction, 41 proportionality and precaution? – Marco Sassòli Increasingly autonomous weapon systems: Accountability and responsibility 45 – Christof Heyns Ethical issues raised by autonomous weapon systems 49 – Peter Asaro Autonomous weapon systems and ethics 53 – Peter Lee Part III: Background paper by the International Committee of the Red Cross 57 Executive summary 57 Introduction 59 Part A: Autonomy in weapon systems 59 Part B: Applying international humanitarian law 74 Part C: Ethical and societal concerns, and the dictates of public conscience 91 Annex 1: Expert meeting agenda 95 Annex 2: List of participants 99 Autonomous weapon systems: Technical, military, legal and humanitarian aspects. -

Irobot Corporation's Intellectual Property∗
iRobot Corporation’s Intellectual Property∗ “At iRobot, we believe there is a better way to accomplish many of the dull, dirty and dangerous tasks that face us today.”1 iRobot designs, develops and markets robots that help people complete ‘dull, dirty or dangerous’ tasks in dynamic real-world situations. The company’s robots use behavior-based, artificial-intelligence systems to undertake complex tasks. In contrast, most robotic manufacturing equipment or entertainment systems are designed to repeat routine actions in specific, known environments. On March 23, 2010, iRobot celebrated 20 years of innovation in robotics. Despite its track record of innovation, iRobot reported an accumulated deficit of $7.6 million in their balance sheet as of yearend 2009 (Exhibit 4). While this deficit had decreased substantially due to annual profits in the recent years (Exhibit 9), management cautioned: Because we operate in a rapidly evolving industry, there are challenges to predicting our future operating results, and we cannot be certain that our revenues will grow at rates that will allow us to maintain profitability during every fiscal quarter, or even every fiscal year. In addition, we only have limited operating history on which you can base your evaluation of our business. Failure to maintain profitability may result in our inability to access capital under our existing credit arrangements. (2009 10-K, p. 19) Background iRobot was founded in 1990 by scientists at the Massachusetts Institute of Technology. Over the subsequent two decades, iRobot developed proprietary technologies incorporating advanced concepts of navigation, mobility, manipulation and artificial intelligence. “iRobot's mission is to change the world by building practical robots that make a difference, while delivering increased value to our shareholders.”2 iRobot became a public company in November 2005, when for the first time, a robot sounded the opening bell on the NASDAQ stock exchange. -

Leave No Stone Unturned, Ideas for Innovations Are Everywhere
30 | ASK MAGAZINE | INSIGHT Leave No Stone Unturned, Ideas for Innovations Are Everywhere BY COLIN ANGLE Maybe an employee comes up with that brilliant idea for a new product. Or perhaps a customer makes a great improvement suggestion. Plus, you always have to keep your eye on the groundbreaking research and development (R&D) taking place in business, academia, and elsewhere. That’s the perpetual challenge: you never know where innovation is going to come from, which is why you need to look for it everywhere. Industry partnerships are one way to develop new products that may never make it to market otherwise. One example is the iRobot PackBot with ICx Fido Explosives Detection Kit. iRobot teamed with ICx Technologies to integrate its explosive -detection technology into the combat- proven PackBot platform. Corporation iRobot courtesy Photo ASK MAGAZINE | 31 At iRobot, talented people and continuous communication Office to develop chemical robots called ChemBots. iRobot will are the cornerstones of innovation. We hire the smartest, most lead a team of leading technical experts from Harvard University curious, and very creative people and communicate with them and the Massachusetts Institute of Technology to incorporate continually. Regularly scheduled all-hands meetings, just one of advances in chemistry, materials science, actuator technologies, the companywide communication efforts, help everyone know electronics, sensors, and fabrication techniques. about the projects being tackled by the other divisions. This basic Through this ChemBots program, robots that reconstitute but critical communication has stimulated a tremendous amount size, shape, and functionality after traversal through complex of cross-fertilization. For example, mine-hunting algorithms environments—the stuff of science fiction—will become real developed for our government and industrial robots were used by tools for soldiers. -

Annual Report 2006 Grow the Business
Grow the business. Lead the industry. Annual Report 2006 Grow the business. Lead the industry. Dear Stockholder, Fiscal 2006 – our first full year as a public company – was a very successful year for iRobot. We delivered record financial results against our aggressive 2006 growth plan while continuing to invest in and develop new products in both of our divisions. The significant progress we made in maturing the operational capabilities of the organization will support our multi-year growth strategy as we move through 2007 and beyond. iRobot’s revenue increased 33 percent this past year, from nearly $142 million in fiscal 2005 to a record $189 million in 2006, the result of growth in both divisions. We also achieved profitability for the third consecutive year, as pre-tax income grew 39 percent to $3.9 million in fiscal 2006. Revenue growth for the year was driven by a 60% increase in our Government & Industrial Robots division, primarily the result of producing and delivering 385 iRobot PackBot robots, bringing our current total to Revenue Growth more than 900 worldwide, and selling associated spares, support and accessories. Fueling the 20% growth of 200 Home Robots revenue was continued demand for our Roomba floor vacuuming robot, especially in the direct sales channel where we more than doubled revenue for 150 the full year, and the initial distribution into the retail channel of our Scooba floor washing robot, which was released late in 2005. $ in Millions 100 Investment in R&D is critical to ensuring the sustained, organic growth of the company. Our outstanding 50 performance in 2006 provided us with the opportunity to make incremental investments that yielded concrete 0 2002 2003 2004 2005 2006 results, including the iRobot PackBot 510, a faster, stronger, easier-to-use, next generation PackBot, and the accelerated development of the iRobot Warrior, our 250-pound, multi-mission platform.