Chapter 7: DFT Filter Bank Solutions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
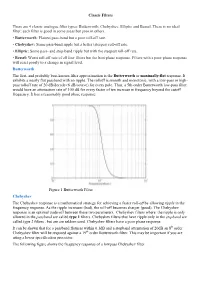
Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used. -

Low Pass Filter Prototype – Maximally Flat
EKT 441 MICROWAVE COMMUNICATIONS MICROWAVE FILTERS 1 INTRODUCTIONWhat is a Microwave filter ? Circuit that controls the frequency response at a certain point in a microwave system provides perfect transmission of signal for frequencies in a certain passband region infinite attenuation for frequencies in the stopband region Attenuation/dB Attenuation/dB 0 0 3 3 10 10 20 20 30 30 40 40 1 2 c 2 FILTER DESIGN METHODS Filter Design Methods Two types of commonly used design methods: - Image Parameter Method - Insertion Loss Method •Image parameter method yields a usable filter Filters designed using the image parameter method consist of a cascade of simpler two port filter sections to provide the desired cutoff frequencies and attenuation characteristics but do not allow the specification of a particular frequency response over the complete operating range. Thus, although the procedure is relatively simple, the design of filters by the image parameter method often must be iterated many times to achieve the desired results. 3 Filter Design by The Insertion Loss Method The perfect filter would have zero insertion loss in the pass- band, infinite attenuation in the stop-band, and a linear phase response in the pass-band. 4 Filter Design by The Insertion Loss Method 5 Filter Design by The Insertion Loss Method 6 Filter Design by The Insertion Loss Method 7 Filter Design by The Insertion Loss Method Practical filter response: Maximally flat: • also called the binomial or Butterworth response, • is optimum in the sense that it provides the flattest possible passband response for a given filter complexity. N 2 PLR 1 k c Equal ripple also known as Chebyshev. -

Composite Lowpass Filter Realized by Image Parameter Method And
Council for Innovative Research International Journal of Computers & Technology www.cirworld.com Volume 4 No. 2, March-April, 2013, ISSN 2277-3061 Composite Lowpass Filter Realized by Image Parameter method and Integrated with Defected Ground Structures Chandan Kumar Ghosh, Arabinda Roy, Susanta Kumar Parui Department of Electronics and Communication Engineering, Dr. B. C. Roy Engineering College, Durgapur, [email protected] Department of Electronics and Tele-Communication Engineering, Bengal Engineering and Science University, Shibpur, India [email protected] Department of Electronics and Tele-Communication Engineering, Bengal Engineering and Science University, Shibpur, India [email protected] ABSTRACT An asymmetric DGS consisting of two square headed slots connected transversely with a rectangular slot is etched in the ground plane underneath a high-low impedance microstrip line. It provides a band-reject filtering characteristics with sharp transition. Thus, it may be modeled as m-derived filter section. Accordingly, T-type LC equivalent circuit is proposed and LC parameters are extracted. A planar composite lowpass filter is designed by image parameter method and implemented by different DGS units. A composite filter requires at least three filter sections, of which two m-derived sections and one constant k-section. In proposed scheme, one such m-derived section is directly replaced by proposed DGS unit, whose cut-off frequency is same as that of designed m-derived section. The other m-derived section implemented by proposed DGS unit divided into equivalent two L-sections which will act as a termination for impedance matching. A constant k-section has been realized by a dumbbell shaped DGS having same cutoff frequency. -

Design of Variable Bandpass Filters Using First Order Allpass Transformation and Coefficient Decimation
> REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < 1 Design of Variable Bandpass Filters Using First Order Allpass Transformation And Coefficient Decimation S. J. Darak and A. P. Vinod E. M-K. Lai School of Computer Engineering School of Engineering and Advanced Technology Nanyang Technological University, Singapore Massey University, Albany, New Zealand {dara0003, asvinod}@ntu.edu.sg [email protected] order allpass transformation. This approach is used in [3] to Abstract — In this paper, the design of a computationally design a filter bank for low power digital hearing aids. It efficient variable bandpass digital filter is presented. The center consists of variable lowpass, bandpass and highpass filters in frequency and bandwidth of this filter can be changed online parallel. However, the complexity of the bandpass filter, which without updating the filter coefficients. The warped filters, obtained by replacing each unit delay of a digital filter with an uses second order allpass transformation, almost double than allpass filter, are widely used for various audio processing that of filters where first order allpass transformation is used. applications. However, warped filters fail to provide variable In [4], adaptive filters are designed using warping technique to bandwidth bandpass responses for a given center frequency using detect the bandpass signals in a broadband signals. The first order allpass transformation. To overcome this drawback, adaptive filters are warped filters designed using reduced our design is accomplished by combining warped filter with the second order transformation and hence they provide fixed coefficient decimation technique. The design example shows that the proposed variable digital filter is simple to design and offers a bandwidth bandpass responses at an arbitrary center total gate count reduction of 36% and 65% over the warped frequency. -

Design of Coupled Resonators Bandpass Filter with Defected Ground Structure
150 Gi-Rae Kim : DESIGN OF COUPLED RESONATORS BANDPASS FILTER WITH DEFECTED GROUND STRUCTURE Design of Coupled Resonators Bandpass Filter with Defected Ground Structure Gi-Rae Kim, Member, KIMICS Abstract— In this paper a four-pole elliptic function coupling between two adjacent resonators. The results of bandpass filter is designed with two ground slots. A research these investigations were used in the design of some four- of microstrip bandpass filters (BPF) using defected ground pole cross coupled planar microwave bandpass Filters structures (DGS) is presented. DGS technique allows designs with a pair of attenuation poles at imposed finite of tight couplings without the necessity of using very narrow frequencies. The Filters were designed with two ground coupling gaps. The simulator Sonnet is used to design the resonator and to calculate the coupling coefficient of the slots. basic coupling structure. Compared to similar microstrip filters without defected ground structure, the simulated performances of these novel structures indicate some II. FILTER CHARACTERISTICS technological advantages. The filter having only one pair of transmission zeros (or Index Terms— compact coupled resonators, bandpass attenuation poles) at finite frequencies gives much filer (BPF), defected ground structure (DGS). improved skirt selectivity, making it a viable intermediate between the Chebyshev and elliptic-function filters, yet with little practical difficulty of physical realization. The I. INTRODUCTION transfer function of this type of filter is IN wireless communication systems, small size and 2 1 high performance filters are needed to reduce the cost and S ()Ω= (1) 21 1()+Ωε 22F improve the system performance. They can be designed in n many different ways. -

Section 5-5: Frequency Transformations
ANALOG FILTERS FREQUENCY TRANSFORMATIONS SECTION 5-5: FREQUENCY TRANSFORMATIONS Until now, only filters using the lowpass configuration have been examined. In this section, transforming the lowpass prototype into the other configurations: highpass, bandpass, bandreject (notch) and allpass will be discussed . Lowpass to Highpass The lowpass prototype is converted to highpass filter by scaling by 1/s in the transfer function. In practice, this amounts to capacitors becoming inductors with a value 1/C, and inductors becoming capacitors with a value of 1/L for passive designs. For active designs, resistors become capacitors with a value of 1/R, and capacitors become resistors with a value of 1/C. This applies only to frequency setting resistor, not those only used to set gain. Another way to look at the transformation is to investigate the transformation in the s plane. The complex pole pairs of the lowpass prototype are made up of a real part, α, and an imaginary part, β. The normalized highpass poles are the given by: α α = Eq. 5-43 HP α2 + β2 and: β β = Eq. 5-44 HP α2 + β2 A simple pole, α0, is transformed to: 1 αω,HP = Eq. 5-45 α0 Lowpass zeros, ωz,lp, are transformed by: 1 ωZ,HP = Eq. 5-46 ωZ,LP In addition, a number of zeros equal to the number of poles are added at the origin. After the normalized lowpass prototype poles and zeros are converted to highpass, they are then denormalized in the same way as the lowpass, that is, by frequency and impedance. As an example a 3 pole 1dB Chebyshev lowpass filter will be converted to a highpass filter. -

Microwave Filters
EEE194 RF Microwave Filters Microwave Filters Passbands and Stopbands in Periodic Structures Periodic structures generally exhibit passband and stopband characteristics in various bands of wave number determined by the nature of the structure. This was originally studied in the case of waves in crystalline lattice structures, but the results are more general. The presence or absence of propagating wave can be determined by inspection of the k-β or ω-β diagram. For our purposes it's enough to know the generality that periodic structures give rise to bands that are passed and bands that are stopped. To construct specific filters, we'd like to be able to relate the desired frequency characteristics to the parameters of the filter structure. The general synthesis of filters proceeds from tabulated low-pass prototypes. Ideally, we can relate the distributed parameters to the corresponding parameters of lumped element prototypes. As we will see, the various forms of filter passband and stopband can be realized in distributed filters as well as in lumped element filters. Over the years, lumped element filters have been developed that are non-minimum phase; that is, the phase characteristics are not uniquely determined by the amplitude characteristics. This technique permits the design of filters for communications systems that could not be constructed using only minimum phase filter concepts. This generally requires coupling between multiple sections, and can be extended to distributed filters. The design of microwave filters is comprehensively detailed in the famous Stanford Research Institute publication1 Microwave Filters, Impedance Matching Networks and Coupling Structures. Richard's Transformation and Kuroda's Identities (λ/8 Lines) Richard's Transformation and Kuroda's Identities focus on uses of λ/8 lines, for which X = jZo. -

Coupling Coefficients of Resonators in Microwave Filter Theory
Progress In Electromagnetics Research B, Vol. 21, 47{67, 2010 COUPLING COEFFICIENTS OF RESONATORS IN MICROWAVE FILTER THEORY V. V. Tyurnev y Kirensky Institute of Physics Siberian Branch of Russian Academy of Sciences Krasnoyarsk 660036, Russia Abstract|This paper is an overview of important concepts and formulas involved in the application of coupling coe±cients of microwave resonators for the design of bandpass ¯lters with a particular emphasis on the frequency dispersion of coupling coe±cients. The presumptions and formulas are classi¯ed into accurate, approximate, and erroneous ones. 1. INTRODUCTION Coupling coe±cients of resonators are widely used in the design of microwave bandpass ¯lters. They o®er a fairly accurate method for a direct synthesis of narrow-band ¯lters and provide initial estimate structure parameters for optimization synthesis of wide-band ¯lters [1{ 4]. Coupling coe±cients together with resonator oscillation modes and their resonant frequencies are the keystones of a universal physical view on microwave bandpass ¯lters. They underlie the intelligence method of ¯lter optimization based on a priory knowledge of physical properties of resonator ¯lters [5{7]. The frequency dispersion of coupling coe±cients is a primary cause of the asymmetrical slopes of the ¯lter passband [8, 9]. Attenuation poles in a ¯lter frequency response are often due to coupling coe±cients becoming null [8]. An energy approach to coupling coe±cients gives a clue to their abnormal dependence on the distance for some resonators [3, 10]. However, there is no generally accepted de¯nition of a resonator coupling coe±cient currently available. The di®erence between Corresponding author: V. -

Synthesis of Filters for Digital Wireless Communications
Synthesis of Filters for Digital Wireless Communications Evaristo Musonda Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Institute of Microwave and Photonics School of Electronic and Electrical Engineering December, 2015 i The candidate confirms that the work submitted is his own, except where work which has formed part of jointly-authored publications has been included. The contribution of the candidate and the other authors to this work has been explicitly indicated below. The candidate confirms that appropriate credit has been given within the report where reference has been made to the work of others. Chapter 2 to Chapter 6 are partly based on the following two papers: Musonda, E. and Hunter, I.C., Synthesis of general Chebyshev characteristic function for dual (single) bandpass filters. In Microwave Symposium (IMS), 2015 IEEE MTT-S International. 2015. Snyder, R.V., et al., Present and Future Trends in Filters and Multiplexers. Microwave Theory and Techniques, IEEE Transactions on, 2015. 63(10): p. 3324- 3360 E. Musonda developed the synthesis technique and wrote the first paper and section IV of the second invited paper. Professor Ian Hunter provided useful editorial comments, suggestions and corrections to the work. Chapter 3 is based on the following two papers: Musonda, E. and Hunter I.C., Design of generalised Chebyshev lowpass filters using coupled line/stub sections. In Microwave Symposium (IMS), 2015 IEEE MTT- S International. 2015. Musonda, E. and I.C. Hunter, Exact Design of a New Class of Generalised Chebyshev Low-Pass Filters Using Coupled Line/Stub Sections. -

Welcome to the Cookbook Filter Guide!
EE133 – Winter 2002 Cookbook Filter Guide Welcome to the Cookbook Filter Guide! Don’t have enough time to spice out that perfect filter before Aunt Thelma comes down for dinner? Well this handout is for you! The following pages detail a fast set of steps towards the design and creation of passive filters for practical use in communications and signal processing. Amaze your friends and neighbors as you do twice the amount of work in half the time! Here’s a brief overview of the steps: ® Specify your filter type ® Implement a low-pass version of your filter ® Transform it to what you really want (high-pass, bandpass, bandstop) ® Simulate and Iterate ® Step 1: What Filter Do I Want? This is where you have to do most of your thinking. It’s no good to cook up a nice steak dinner if Auntie Thelma turned vegetarian last year. Here are the specifications that are most often quoted with filters: Filter Type (Low-Pass, High-Pass, Band-Pass, Band-Stop) Center frequency (rad/s or Hz) Bandwidth (rad/s or Hz) Cut-off/Roll-off rate (dB) Minimum Attenuation Required in Stopband Input Impedance (ohms) Output Impedance (ohms) Overshoot in Step Response Ringing in Step Response We will be creating filters through a method known as the insertion loss method. Insertion Loss, or the Power Loss Ratio PLR.is defined as: PowerSource 1 PLR = = 2 PowerDelivered 1- G(w) G is our famliar reflection coefficient. It turns out that this is expressible in the following form of : M(w2 ) P =1 + LR N(w 2) Where M and N are two real polynomials. -

The Simulation, Design and Implementation of Bandpass Filters in Rectangular Waveguides
Electrical and Electronic Engineering 2012, 2(3): 152-157 DOI: 10.5923/j.eee.20120203.08 The Simulation, Design and Implementation of Bandpass Filters in Rectangular Waveguides Sarun Choocadee, Somsak Akatimagool* Department of Teaching Training in Electrical Engineering, Faculty of Technical Education, King Mongkut’s University of Technology North Bangkok, Thailand Abstract This paper presents the simulation, design and implementation of bandpass filters in rectangular waveguides. The filters are simulated and designed by using a numerical analysis program based on the Wave Iterative Method (WIM) called WFD (Waveguide Filter Design) simulation. This simulation program can analyze the electrical network of filters. The sample waveguide filter is designed based on a proposed structure consisting of three circuits serving as a simple bandpass filter with two inductive irises and three inductive irises in a cascade. We determined that the operating frequency was equal to approximately 4.20-4.84 GHz. The waveguide filters were then implemented using an aluminum material. The analyzed results for the inductive iris obtained with the WFD program agree well with the results of CST Microwave Stu- dio®. Finally, the measured results of sample waveguide filters are consistent with the simulation tool. Keywords Inductive Irises, Simulation Program, Bandpass Filter, Waveguide Filters Design, Wave Iterative Method Recently reported waveguide filter has several structures. 1. Introduction Many accurate techniques have also been proposed but have complex algorithms[9-12]. The Ref.[9] explains a new Presently, the development of technologies for wireless method based on inverse scattering theory of single-mode communications, particularly for use in the microwave fre- planar waveguides in order to obtain a desired TE-mode quency range, is critical to developing the economy and profile. -

General Coupling Matrix Synthesis Methods for Chebyshev Filtering Functions
IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. 47, NO. 4, APRIL 1999 433 General Coupling Matrix Synthesis Methods for Chebyshev Filtering Functions Richard J. Cameron, Senior Member, IEEE Abstract— Methods are presented for the generation of the In order to cope with the increasing demand for capacity transfer polynomials, and then the direct synthesis of the cor- in restricted spectral bandwidths, specifications for channel responding canonical network coupling matrices for Chebyshev filter rejections have tended to become asymmetric. This is (i.e., prescribed-equiripple) filtering functions of the most general kind. A simple recursion technique is described for the generation particularly true for the front-end transmit/receive (Tx/Rx) of the polynomials for even- or odd-degree Chebyshev filter- diplexers in the base stations of mobile communications sys- ing functions with symmetrically or asymmetrically prescribed tems, where very high rejection levels (sometimes as high transmission zeros and/or group delay equalization zero pairs. as 120 dB) are needed from the Rx filter over the closely The method for the synthesis of the coupling matrix for the cor- neighboring Tx channel’s usable bandwidth and vice versa responding single- or double-terminated network is then given. Finally, a novel direct technique, not involving optimization, for to prevent Tx-to-Rx interference. On the outer sides of the reconfiguring the matrix into a practical form suitable for real- Tx and Rx channels, rejection requirements tend to be less ization with microwave resonator technology is introduced. These severe. Such asymmetric rejection specifications are best met universal methods will be useful for the design of efficient high- with asymmetric filtering characteristics, reducing filter degree performance microwave filters in a wide variety of technologies to a minimum and, therefore, minimizing insertion loss, in- for application in space and terrestrial communication systems.