Functional Programming Languages (LISP)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Administering Unidata on UNIX Platforms
C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta UniData Administering UniData on UNIX Platforms UDT-720-ADMU-1 C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Notices Edition Publication date: July, 2008 Book number: UDT-720-ADMU-1 Product version: UniData 7.2 Copyright © Rocket Software, Inc. 1988-2010. All Rights Reserved. Trademarks The following trademarks appear in this publication: Trademark Trademark Owner Rocket Software™ Rocket Software, Inc. Dynamic Connect® Rocket Software, Inc. RedBack® Rocket Software, Inc. SystemBuilder™ Rocket Software, Inc. UniData® Rocket Software, Inc. UniVerse™ Rocket Software, Inc. U2™ Rocket Software, Inc. U2.NET™ Rocket Software, Inc. U2 Web Development Environment™ Rocket Software, Inc. wIntegrate® Rocket Software, Inc. Microsoft® .NET Microsoft Corporation Microsoft® Office Excel®, Outlook®, Word Microsoft Corporation Windows® Microsoft Corporation Windows® 7 Microsoft Corporation Windows Vista® Microsoft Corporation Java™ and all Java-based trademarks and logos Sun Microsystems, Inc. UNIX® X/Open Company Limited ii SB/XA Getting Started The above trademarks are property of the specified companies in the United States, other countries, or both. All other products or services mentioned in this document may be covered by the trademarks, service marks, or product names as designated by the companies who own or market them. License agreement This software and the associated documentation are proprietary and confidential to Rocket Software, Inc., are furnished under license, and may be used and copied only in accordance with the terms of such license and with the inclusion of the copyright notice. -

CSC 242: Artificial Intelligence
CSC 242: Artificial Intelligence Course website: www.cs.rochester.edu/u/kyros/courses/csc242 Instructor: Kyros Kutulakos Office: 623 CSB Extension: x5-5860 Email: [email protected] Hours: TR 3:30-4:30 (or by appointment) TA: Joel Tetreault Email: [email protected] Hours: M 1:00-2:00 Recitations: TBA Textbooks: Russell & Norvig, Artificial Intelligence Wilensky, Common LISPcraft Another very good LISP textbook: Winston & Horn, LISP (Addison-Wesley) Common Lisp • LISP is one of the most common “AI programming languages” • LISP (=LISt Processing) is a language whose main power is in manipulating lists of symbols: (a b c (d e f (g h))) arithmetic operations are also included (sqrt (+ (* 3 3) (* 4 4))) • Lisp is a general-purpose, interpreter-based language • All computation consists of expression evaluations: lisp-prompt>(sqrt (+ (* 3 3) (* 4 4))) lisp-prompt> 25 • Since data are list structures and programs are list structures, we can manipulate programs just like data • Lisp is the second-oldest high-level programming language (after Fortran) Getting Started • Command-line invocation unix-prompt>cl system responds with loading & initialization messages followed by a Lisp prompt USER(1): whenever you have balanced parentheses & hit return, the value of the expression (or an error message) are returned USER(1): (+ 1 2) 3 saying “hello” USER(2): ‘hello HELLO USER(3): “Hello” “Hello” • Exiting Lisp: USER(2):(exit) unix-prompt> Getting Started (cont.) • Reading a file f that is in the same directory from which you are running Lisp: -

MELT a Translated Domain Specific Language Embedded in the GCC
MELT a Translated Domain Specific Language Embedded in the GCC Compiler Basile STARYNKEVITCH CEA, LIST Software Safety Laboratory, boˆıte courrier 94, 91191 GIF/YVETTE CEDEX, France [email protected] [email protected] The GCC free compiler is a very large software, compiling source in several languages for many targets on various systems. It can be extended by plugins, which may take advantage of its power to provide extra specific functionality (warnings, optimizations, source refactoring or navigation) by processing various GCC internal representations (Gimple, Tree, ...). Writing plugins in C is a complex and time-consuming task, but customizing GCC by using an existing scripting language inside is impractical. We describe MELT, a specific Lisp-like DSL which fits well into existing GCC technology and offers high-level features (functional, object or reflexive programming, pattern matching). MELT is translated to C fitted for GCC internals and provides various features to facilitate this. This work shows that even huge, legacy, software can be a posteriori extended by specifically tailored and translated high-level DSLs. 1 Introduction GCC1 is an industrial-strength free compiler for many source languages (C, C++, Ada, Objective C, Fortran, Go, ...), targetting about 30 different machine architectures, and supported on many operating systems. Its source code size is huge (4.296MLOC2 for GCC 4.6.0), heterogenous, and still increasing by 6% annually 3. It has no single main architect and hundreds of (mostly full-time) contributors, who follow strict social rules 4. 1.1 The powerful GCC legacy The several GCC [8] front-ends (parsing C, C++, Go . -

Common Lispworks User Guide
LispWorks® for the Windows® Operating System Common LispWorks User Guide Version 5.1 Copyright and Trademarks Common LispWorks User Guide (Windows version) Version 5.1 February 2008 Copyright © 2008 by LispWorks Ltd. All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of LispWorks Ltd. The information in this publication is provided for information only, is subject to change without notice, and should not be construed as a commitment by LispWorks Ltd. LispWorks Ltd assumes no responsibility or liability for any errors or inaccuracies that may appear in this publication. The software described in this book is furnished under license and may only be used or copied in accordance with the terms of that license. LispWorks and KnowledgeWorks are registered trademarks of LispWorks Ltd. Adobe and PostScript are registered trademarks of Adobe Systems Incorporated. Other brand or product names are the registered trade- marks or trademarks of their respective holders. The code for walker.lisp and compute-combination-points is excerpted with permission from PCL, Copyright © 1985, 1986, 1987, 1988 Xerox Corporation. The XP Pretty Printer bears the following copyright notice, which applies to the parts of LispWorks derived therefrom: Copyright © 1989 by the Massachusetts Institute of Technology, Cambridge, Massachusetts. Permission to use, copy, modify, and distribute this software and its documentation for any purpose and without fee is hereby granted, pro- vided that this copyright and permission notice appear in all copies and supporting documentation, and that the name of M.I.T. -

Dell EMC Powerstore CLI Guide
Dell EMC PowerStore CLI Guide May 2020 Rev. A01 Notes, cautions, and warnings NOTE: A NOTE indicates important information that helps you make better use of your product. CAUTION: A CAUTION indicates either potential damage to hardware or loss of data and tells you how to avoid the problem. WARNING: A WARNING indicates a potential for property damage, personal injury, or death. © 2020 Dell Inc. or its subsidiaries. All rights reserved. Dell, EMC, and other trademarks are trademarks of Dell Inc. or its subsidiaries. Other trademarks may be trademarks of their respective owners. Contents Additional Resources.......................................................................................................................4 Chapter 1: Introduction................................................................................................................... 5 Overview.................................................................................................................................................................................5 Use PowerStore CLI in scripts.......................................................................................................................................5 Set up the PowerStore CLI client........................................................................................................................................5 Install the PowerStore CLI client.................................................................................................................................. -
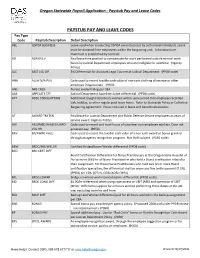
Oregon Statewide Payroll Application ‐ Paystub Pay and Leave Codes
Oregon Statewide Payroll Application ‐ Paystub Pay and Leave Codes PAYSTUB PAY AND LEAVE CODES Pay Type Code Paystub Description Detail Description ABL OSPOA BUSINESS Leave used when conducting OSPOA union business by authorized individuals. Leave must be donated from employees within the bargaining unit. A donation/use maximum is established by contract. AD ADMIN LV Paid leave time granted to compensate for work performed outside normal work hours by Judicial Department employees who are ineligible for overtime. (Agency Policy) ALC ASST LGL DIF 5% Differential for Assistant Legal Counsel at Judicial Department. (PPDB code) ANA ALLW N/A PLN Code used to record taxable cash value of non-cash clothing allowance or other employee fringe benefit. (P050) ANC NRS CRED Nurses credentialing per CBA ASA APPELATE STF Judicial Department Appellate Judge differential. (PPDB code) AST ADDL STRAIGHTTIME Additional straight time hours worked within same period that employee recorded sick, holiday, or other regular paid leave hours. Refer to Statewide Policy or Collective Bargaining Agreement. Hours not used in leave and benefit calculations. AT AWARD TM TKN Paid leave for Judicial Department and Public Defense Service employees as years of service award. (Agency Policy) AW ASSUMED WAGES-UNPD Code used to record and track hours of volunteer non-employee workers. Does not VOL HR generate pay. (P050) BAV BP/AWRD VALU Code used to record the taxable cash value of a non-cash award or bonus granted through an agency recognition program. Not PERS subject. (P050 code) BBW BRDG/BM/WELDR Certified Bridge/Boom/Welder differential (PPDB code) BCD BRD CERT DIFF Board Certification Differential for Nurse Practitioners at the Oregon State Hospital of five percent (5%) for all Nurse Practitioners who hold a Board certification related to their assignment. -

Small Group Instructional Diagnosis: Final Report
DOCUMENT RESUME JC 820 333 , ED 217 954 AUTHOR Clark, D. Joseph; Redmond, Mark V. TITLE Small Group Instructional Diagnosis: Final Report. INSTITUTION Washington Univ., Seattle. Dept. of Biology c Education. ., 'SPONS AGENCY Fund for the Improwsent of Postsecondary Education . (ED), Washington, D.C. , PUB DATE [82] NOTE 21p.; Appendices mentioned in the report are not _ included. EDRS PRICE , 401/PC01 Plus Postage. DESCRIPTORS *Course Evaluation; *Evaluation Methods; *Instructional Improvement; Postsecondary Education; *Student Evaluation of Teacher Performance;- tudent , Reaction; *Teacher Attitudes; Teacher Workshop IDENTIFIERS *Small group Instructional Diagnosis, ABSTRACT- A procedure for student evaluation andfeedback on faculty instruction was developed at the University of Washington. The system involved the use of,faculty members as facilitatorsin ,conducting Small Group Instructional Diagnosis (SGID) to generate student feedback to instructors about- the courses' strengths, areas needing improvement, and suggestions for bringing about these improvements. The SGID.procedure involves a number of steps:contact between the facilitator and instructor; classroomintervention to ascertain student opinions; a feedback session between facilitator and instructor; instructor. review of the SGID with the class;and ,a follow-up session between the facilitator and instructor.Following the development of the SGID process, handouts andvideotapes were produced to explain the procedure and the SGID technique was demonstrated in over 130 classes -

LS JK BUILDER KIT 2007-2011 Jeep Wrangler JK Installation Guide
LS JK BUILDER KIT 2007-2011 Jeep Wrangler JK Installation Guide Install Guide © Table of contents: Preface………………………………………………………………… ………………….….….…3 Part 1 Power options…………………………………………………………………….….…..…4 Part 2 The LS JK…………………………………………………………………………….….….6 Part 3 LS engines…………………………………………………………………………….….…7 Part 4 Operating systems………………………………………………………………………..10 Part 5 Gen IV LS engine features……………………………………………………………….11 Part 6 Transmissions……………………………………………………………………………..12 Part 7 Transfer cases……………………………………………………………………………..13 Part 8 MoTech basic builder kit contents……………………………………………………….14 Part 9 MoTech basic builder kit photo ID table…………………………………………………18 Part 10 MoTech Basic Kit Installation Overview and Shop Tools Required………………...20 Part 11 Prepping the vehicle………………………………………………………………..……21 Part 12 Removing the body……………………………………………………………………....21 Part 13 Prepping the chassis…………………………………………………………………..…28 Part 14 Installing the powertrain………………………………………………………………….31 Part 15 Accessory drive………………………………………………… ………………………36 Part 16 Wiring the LS JK…………………………………………………………………………..39 Appendix ……………………………………………………………………………………………52 Pentstar fan installation……………………………………………………………………52 Wiring diagrams…………………………………………………………………………….53 241J Input gear installation………………………………………………………………..56 Manual to automatic conversion……………………………………………………….….81 Torque specification GM and Jeep……………………………………………………….83 Radiator hose guide…………………………………………………………………...…...86 LS JK master part list…………………………………………………………………........87 2 Install Guide © Preface: The Wrangler -

GNU M4, Version 1.4.7 a Powerful Macro Processor Edition 1.4.7, 23 September 2006
GNU M4, version 1.4.7 A powerful macro processor Edition 1.4.7, 23 September 2006 by Ren´eSeindal This manual is for GNU M4 (version 1.4.7, 23 September 2006), a package containing an implementation of the m4 macro language. Copyright c 1989, 1990, 1991, 1992, 1993, 1994, 2004, 2005, 2006 Free Software Foundation, Inc. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License.” i Table of Contents 1 Introduction and preliminaries ................ 3 1.1 Introduction to m4 ............................................. 3 1.2 Historical references ............................................ 3 1.3 Invoking m4 .................................................... 4 1.4 Problems and bugs ............................................. 8 1.5 Using this manual .............................................. 8 2 Lexical and syntactic conventions ............ 11 2.1 Macro names ................................................. 11 2.2 Quoting input to m4........................................... 11 2.3 Comments in m4 input ........................................ 11 2.4 Other kinds of input tokens ................................... 12 2.5 How m4 copies input to output ................................ 12 3 How to invoke macros........................ -

The Evolution of Lisp
1 The Evolution of Lisp Guy L. Steele Jr. Richard P. Gabriel Thinking Machines Corporation Lucid, Inc. 245 First Street 707 Laurel Street Cambridge, Massachusetts 02142 Menlo Park, California 94025 Phone: (617) 234-2860 Phone: (415) 329-8400 FAX: (617) 243-4444 FAX: (415) 329-8480 E-mail: [email protected] E-mail: [email protected] Abstract Lisp is the world’s greatest programming language—or so its proponents think. The structure of Lisp makes it easy to extend the language or even to implement entirely new dialects without starting from scratch. Overall, the evolution of Lisp has been guided more by institutional rivalry, one-upsmanship, and the glee born of technical cleverness that is characteristic of the “hacker culture” than by sober assessments of technical requirements. Nevertheless this process has eventually produced both an industrial- strength programming language, messy but powerful, and a technically pure dialect, small but powerful, that is suitable for use by programming-language theoreticians. We pick up where McCarthy’s paper in the first HOPL conference left off. We trace the development chronologically from the era of the PDP-6, through the heyday of Interlisp and MacLisp, past the ascension and decline of special purpose Lisp machines, to the present era of standardization activities. We then examine the technical evolution of a few representative language features, including both some notable successes and some notable failures, that illuminate design issues that distinguish Lisp from other programming languages. We also discuss the use of Lisp as a laboratory for designing other programming languages. We conclude with some reflections on the forces that have driven the evolution of Lisp. -

Allegro CL User Guide
Allegro CL User Guide Volume 1 (of 2) version 4.3 March, 1996 Copyright and other notices: This is revision 6 of this manual. This manual has Franz Inc. document number D-U-00-000-01-60320-1-6. Copyright 1985-1996 by Franz Inc. All rights reserved. No part of this pub- lication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means electronic, mechanical, by photocopying or recording, or otherwise, without the prior and explicit written permission of Franz incorpo- rated. Restricted rights legend: Use, duplication, and disclosure by the United States Government are subject to Restricted Rights for Commercial Software devel- oped at private expense as specified in DOD FAR 52.227-7013 (c) (1) (ii). Allegro CL and Allegro Composer are registered trademarks of Franz Inc. Allegro Common Windows, Allegro Presto, Allegro Runtime, and Allegro Matrix are trademarks of Franz inc. Unix is a trademark of AT&T. The Allegro CL software as provided may contain material copyright Xerox Corp. and the Open Systems Foundation. All such material is used and distrib- uted with permission. Other, uncopyrighted material originally developed at MIT and at CMU is also included. Appendix B is a reproduction of chapters 5 and 6 of The Art of the Metaobject Protocol by G. Kiczales, J. des Rivieres, and D. Bobrow. All this material is used with permission and we thank the authors and their publishers for letting us reproduce their material. Contents Volume 1 Preface 1 Introduction 1.1 The language 1-1 1.2 History 1-1 1.3 Format -

ESA: a CLIM Library for Writing Emacs-Style Applications
ESA: A CLIM Library for Writing Emacs-Style Applications Robert Strandh Troels Henriksen LaBRI, Université Bordeaux 1 DIKU, University of Copenhagen 351, Cours de la Libération Universitetsparken 1, Copenhagen 33405 Talence Cedex [email protected] France [email protected] David Murray Christophe Rhodes ADMurray Associates Goldsmiths, University of London 10 Rue Carrier Belleuse, 75015 Paris New Cross Road, London, SE14 6NW [email protected] [email protected] ABSTRACT style applications. The central distinguishing feature of an We describe ESA (for Emacs-Style Application), a library Emacs-style application, for our purposes, is that it uses for writing applications with an Emacs look-and-feel within short sequences of keystrokes as the default method of in- the Common Lisp Interface Manager. The ESA library voking commands, and only occasionally requires the user to takes advantage of the layered design of CLIM to provide a type the full name of the command in a minibuffer. A spe- command loop that uses Emacs-style multi-keystroke com- cial keystroke (M-x) is used to invoke commands by name. mand invocation. ESA supplies other functionality for writ- This interaction style is substantially different from the one ing such applications such as a minibuffer for invoking ex- provided by CLIM by default, and therefore required us to tended commands and for supplying command arguments, write a different CLIM top level. Fortunately, CLIM was Emacs-style keyboard macros and numeric arguments, file designed to make this not only possible but fairly straight- and buffer management, and more. ESA is currently used forward, as the implementation of a replacement top level in two major CLIM applications: the Climacs text editor can build on the protocol layers beneath, just as the default (and the Drei text gadget integrated with the McCLIM im- top level is built.