Particle Systems for Efficient and Accurate High-Order Finite Element Visualization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
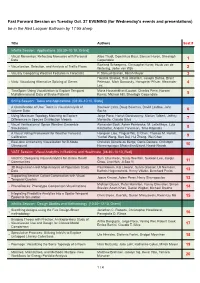
Tuesday's Evening Fast Forward Session
Fast Forward Session on Tuesday Oct. 27 EVENING (for Wednesday's events and presentations) be in the Red Lacquer Ballroom by 17:55 sharp Title Authors Seat # InfoVis Session: Applications [08:30–10:10, Grand] Visual Mementos: Reflecting Memories with Personal Alice Thudt, Dominikus Baur, Samuel Huron, Sheelagh - Data Carpendale 1 Roeland Scheepens, Christophe Hurter, Huub van de - Visualization, Selection, and Analysis of Traffic Flows Wetering, Jarke van Wijk 2 - Visually Comparing Weather Features in Forecasts P. Samuel Quinan, Miriah Meyer 3 Hendrik Strobelt, Bilal Alsallakh, Joseph Botros, Brant - Vials: Visualizing Alternative Splicing of Genes Peterson, Mark Borowsky, Hanspeter Pfister, Alexander 4 Lex TimeSpan: Using Visualization to Explore Temporal Mona Hosseinkhani Loorak, Charles Perin, Noreen - Multidimensional Data of Stroke Patients Kamal, Michael Hill, Sheelagh Carpendale 5 SciVis Session: Tasks and Applications [08:30–10:10, State] A Classification of User Tasks in Visual Analysis of Bireswar Laha, Doug Bowman, David Laidlaw, John - Volume Data Socha 6 Using Maximum Topology Matching to Explore Jorge Poco, Harish Doraiswamy, Marian Talbert, Jeffrey - Differences in Species Distribution Models Morisette, Claudio Silva 7 Visual Verification of Space Weather Ensemble Alexander Bock, Asher Pembroke, M. Leila Mays, Lutz - Simulations Rastaetter, Anders Ynnerman, Timo Ropinski 8 A Visual Voting Framework for Weather Forecast Hongsen Liao, Yingcai Wu, Li Chen, Thomas M. Hamill, - Calibration Yunhai Wang, Kan Dai, Hui Zhang, Wei -

Scientific Visualization
Report from Dagstuhl Seminar 11231 Scientific Visualization Edited by Min Chen1, Hans Hagen2, Charles D. Hansen3, and Arie Kaufman4 1 University of Oxford, GB, [email protected] 2 TU Kaiserslautern, DE, [email protected] 3 University of Utah, US, [email protected] 4 SUNY – Stony Brook, US, [email protected] Abstract This report documents the program and the outcomes of Dagstuhl Seminar 11231 “Scientific Visualization”. Seminar 05.–10. June, 2011 – www.dagstuhl.de/11231 1998 ACM Subject Classification I.3 Computer Graphics, I.4 Image Processing and Computer Vision, J.2 Physical Sciences and Engineering, J.3 Life and Medical Sciences Keywords and phrases Scientific Visualization, Biomedical Visualization, Integrated Multifield Visualization, Uncertainty Visualization, Scalable Visualization Digital Object Identifier 10.4230/DagRep.1.6.1 1 Executive Summary Min Chen Hans Hagen Charles D. Hansen Arie Kaufman License Creative Commons BY-NC-ND 3.0 Unported license © Min Chen, Hans Hagen, Charles D. Hansen, and Arie Kaufman Scientific Visualization (SV) is the transformation of abstract data, derived from observation or simulation, into readily comprehensible images, and has proven to play an indispensable part of the scientific discovery process in many fields of contemporary science. This seminar focused on the general field where applications influence basic research questions on one hand while basic research drives applications on the other. Reflecting the heterogeneous structure of Scientific Visualization and the currently unsolved problems in the field, this seminar dealt with key research problems and their solutions in the following subfields of scientific visualization: Biomedical Visualization: Biomedical visualization and imaging refers to the mechan- isms and techniques utilized to create and display images of the human body, organs or their components for clinical or research purposes. -

Data Visualization by Nils Gehlenborg
Data Visualization Nils Gehlenborg ([email protected]) Center for Biomedical Informatics / Harvard Medical School Cancer Program / Broad Institute of MIT and Harvard ISMB/ECCB 2011 http://www.biovis.net Flyers at ISCB booth! Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg A good sketch is better than a long speech. Napoleon Bonaparte Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg Minard 1869 Napoleon’s March on Moscow Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg 4 I believe when I see it. Unknown Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg Anscombe 1973, The American Statistician Anscombe’s Quartet mean(X) = 9, var(X) = 11, mean(Y) = 7.5, var(Y) = 4.12, cor(X,Y) = 0.816, linear regression line Y = 3 + 0.5*X Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg 6 Anscombe 1973, The American Statistician Anscombe’s Quartet Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg 7 Exploration: Hypothesis Generation trends gaps outliers clusters - A large data set is given and the goal is to learn something about it. - Visualization is employed to perform pattern detection using the human visual system. - The goal is to generate hypotheses that can be tested with statistical methods or follow-up experiments. Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg 8 Visualization Use Cases Presentation Confirmation Exploration Data Visualization / ISMB/ECCB 2011 / Nils Gehlenborg 9 Definition The use of computer-supported, interactive, visual representations of data to amplify cognition. Stu Card, Jock Mackinlay & Ben Shneiderman Computer-based visualization systems provide visual representations of datasets intended to help people carry out some task more effectively.effectively. -

Pop-Out, Illusions, Interaction
Pop-Out, Illusions, Interaction DS 4200 FALL 2020 Prof. Cody Dunne NORTHEASTERN UNIVERSITY Slides and inspiration from Michelle Borkin, Krzysztof Gajos, Hanspeter Pfister, Miriah Meyer, Jonathan Schwabish, and David Sprague 1 CHECK-IN 2 PREVIOUSLY, ON DS 4200… 4 Color Vocabulary and Perceptual Ordering Darkness (Lightness) Saturation Hue ? ? Based on Slides by Miriah Meyer, Tamara Munzner 5 Color Deficiencies (Color Blindness) Based on Slides by Hanspeter Pfister, Maureen Stone 6 Check your images/colormaps for issues! http://www.vischeck.com/vischeck/vischeckImage.php https://www.color-blindness.com/coblis-color-blindness-simulator/ 7 Color Brewer http://colorbrewer2.org 8 Color Advice Summary Use a limited hue palette • Control color “pop out” with low-saturation colors • Avoid clutter from too many competing colors Use neutral backgrounds • Control impact of color • Minimize simultaneous contrast Use Color Brewer etc. for picking scales Don’t forget aesthetics! Based on Slides by Hanspeter Pfister, Maureen Stone 9 NOW, ON DS 4200… 10 POP-OUT EFFECTS 15 POP-OUT EFFECTS COLOR Healey, 2012 16 POP-OUT EFFECTS SHAPE Healey, 2012 17 POP-OUT EFFECTS “CONJUNCTION” (HARDER TO FIND RED CIRCLE!) Healey, 2012 18 POP-OUT EFFECTS MOTION Healey, 2012 19 POP-OUT EFFECTS Healey, 2012 20 POP-OUT EFFECTS Healey, 2012 21 Use these “popout” effects to help design effective visualizations! (E.g., draw viewer’s attention to main points, effective redundant encodings, etc.) Ware, VTFD 22 Discriminability and Separability The question of discriminability is: if you encode data using a particular visual channel, are the differences between items perceptible to the human as intended? Munzner, VAD 23 Textures easy hard Ware, VTFD 25 Textures: Interference Ware, VTFD 26 ILLUSIONS AND TRICKS 28 Visual Attention & Change Blindness 30 Visual Attention & Change Blindness Task: Identify the lumps/nodules in the patient’s lungs to look for cancer or abnormal growth. -

Eurovis 2019 Eurographics / IEEE VGTC Conference on Visualization 2019
EuroVis 2019 Eurographics / IEEE VGTC Conference on Visualization 2019 Porto, Portugal June 3 – 7, 2019 Organized by EUROGRAPHICS THE EUROPEAN ASSOCIATION FOR COMPUTER GRAPHICS IEEE Visualization and Graphics Technical Committee General Chairs Alfredo Ferreira – INESC-ID, Instituto Superior Técnico, Universidade de Lisboa Joaquim A. Jorge – INESC-ID, Instituto Superior Técnico, Universidade de Lisboa Full Papers Chairs Michael Gleicher – University of Wisconsin Ivan Viola – KAUST Heike Leitte – TU Kaiserslautern STARs Chairs Robert S. Laramee – Swansea University Steffen Oeltze – Dept. of Neurology, University of Magdeburg Michael Sedlmair – Jacobs University Short Papers Chairs Jimmy Johansson – Linköping University Filip Sadlo – Heidelberg University G. Elisabeta Marai – University of Illinois at Chicago Posters Chairs João Madeiras Pereira – Universidade de Lisboa Renata Raidou – TU Wien DOI: 10.1111/cgf.13725 https://www.eg.org https://diglib.eg.org Eurographics Conference on Visualization (EuroVis) 2019 Volume 38 (2019), Number 3 M. Gleicher, H. Leitte, and I. Viola (Guest Editors) Organizers and Sponsors Eurographics Conference on Visualization (EuroVis) 2019 Volume 38 (2019), Number 3 M. Gleicher, H. Leitte, and I. Viola (Guest Editors) Preface EuroVis 2019, the 21th Eurographics / IEEE VGTC Conference on Visualization, was held in Porto, Portugal, on June 3-7, 2019. The proceedings are published as a special issue of the Eurographics Computer Graphics Forum journal. The conference, which started in 1990 as the Eurographics Workshop on Visualization in Scientific Com- puting and was called VisSym after 1999, has been known as EuroVis since 2005. EuroVis attracts contributions that broadly cover the field of visualization. Topics include visualization techniques for spatial data, such as volumet- ric, tensor, and vector field datasets, and for non-spatial data, such as graphs, text, and high-dimensional datasets. -

Particle-Based Sampling and Meshing of Surfaces in Multimaterial Volumes
Particle-Based Sampling and Meshing of Surfaces in Multimaterial Volumes The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Meyer, Miriah, Ross Whitaker, Robert M. Kirby, Christian Ledergerber, and Hanspeter Pfister. 2008. Particle-based sampling and meshing of surfaces in multimaterial volumes. IEEE Transactions on Visualization and Computer Graphics 14(6): 1539-1546. Published Version doi:10.1109/TVCG.2008.154 Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:4100251 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP Particle-based Sampling and Meshing of Surfaces in Multimaterial Volumes Miriah Meyer, Ross Whitaker, Member, IEEE, Robert M. Kirby, Member, IEEE, Christian Ledergerber, and Hanspeter Pfister, Senior Member, IEEE Abstract— Methods that faithfully and robustly capture the geometry of complex material interfaces in labeled volume data are im- portant for generating realistic and accurate visualizations and simulations of real-world objects. The generation of such multimaterial models from measured data poses two unique challenges: first, the surfaces must be well-sampled with regular, efficient tessella- tions that are consistent across material boundaries; and second, the resulting meshes must respect the nonmanifold geometry of the multimaterial interfaces. This paper proposes a strategy for sampling and meshing multimaterial volumes using dynamic particle systems, including a novel, differentiable representation of the material junctions that allows the particle system to explicitly sam- ple corners, edges, and surfaces of material intersections. -

New Faculty Members and Postdoctoral Fellows Spill the Beans
New faculty members and postdoctoral fellows spill the beans Alark Joshi ∗ Jeffrey Heer† Gordon L. Kindlmann‡ Miriah Meyer§ Yale University Stanford University University of Chicago Harvard University ABSTRACT • Strategically scheduling your interviews Applying for an academic position can be a daunting task. In this • Cultivating internal champions panel, we talk with a few new faculty members in the field of vi- sualization and find out more about the process. We share some • Planning and practicing ones job talk insights into how does one go about finding an academic position, what kind of material is required for the application packet, how do • Remembering to have fun with the interview process you prepare the material, how does one apply for the faculty posi- • Framing negotiation as enabling research success tion, what happens on the day of the job interview, what would new faculty members have wished they had known before they applied • Deciding whats right for you - An exercise in multi-objective and much more. optimization (?) With many universities facing budget cuts in this economy, the likelihood of new faculty positions opening up may be slim. We • And a good problem to have: the pain of rejecting offers discuss the wonderful alternative of taking up a postdoctoral posi- tion. Postdoctoral fellows on the panel will share their experiences Biosketch: and discuss what the position entails. Jeffrey Heer is a newly minted Assistant Professor of Com- puter Science at Stanford University, where he works on human- 1 INTRODUCTION computer interaction, visualization, and social computing. Heer’s For graduate students and postdoctoral fellows, academic careers research has produced novel visualization techniques for explor- always seem to be a challenging proposition. -

Miriah Meyer University of Utah Cs6964 | Jan 10 2012
cs6964 | Jan 10 2012 INFORMATION VISUALIZATION Miriah Meyer University of Utah cs6964 | Jan 10 2012 INFORMATION VISUALIZATION Miriah Meyer University of Utah slide acknowledgements: Hanspeter Pfister, Harvard University Jeff Heer, Stanford University - WHAT - WHY - WHO - HOW 3 - WHAT - WHY - WHO - HOW 4 data INDUSTRIAL REVOLUTION OF DATA Joe Hellerstein, UC Berkley, 2008 HOW MUCH DATA IS THERE? 6 2010: 1.2 zetabytes 2011: 1.8 zetabytes zetabyte ~= 1,000,000,000,000,000,000,000,000 or 1024 200x all words ever spoken by humans 9x increase over 5 years [Gantz et al 2011] http://www.jamesshuggins.com/h/tek1/how_big.htm7 The ability to take data—to be able to understand it, to process it, to extract value from it, to visualize it, to communicate it—that’s going to be a hugely important skill in the next decades, ... because now we really do have essentially free and ubiquitous data. So the complimentary scarce factor is the ability to understand that data and extract value from it. Hal Varian, Google’s Chief Economist The McKinsey Quarterly, Jan 2009 8 COGNITION IS LIMITED 9 10 MTHIVLWYADCEQGHKILKMTWYN ARDCAIREQGHLVKMFPSTWYARN GFPSVCEILQGKMFPSNDRCEQDIFP SGHLMFHKMVPSTWYACEQTWRN 11 MTHIVLWYADCEQGHKILKMTWYN ARDCAIREQGHLVKMFPSTWYARN GFPSVCEILQGKMFPSNDRCEQDIFP SGHLMFHKMVPSTWYACEQTWRN 12 VISUALIZATION . 1) uses perception to free up cognition 13 MEMORY IS LIMITED 14 34 calculation exercise . x 28 15 79 calculation exercise . x 16 16 VISUALIZATION . 1) uses perception to free up cognition 2) serves as an external aid to augment working memory 17 vi⋅su⋅al⋅i⋅za⋅tion -

Eurovis 2015 Eurographics Conference on Visualization 2015 Cagliari, Sardinia, Italy May 25 – 29, 2015
EuroVis 2015 Eurographics Conference on Visualization 2015 Cagliari, Sardinia, Italy May 25 – 29, 2015 Organized by EUROGRAPHICS THE EUROPEAN ASSOCIATION IEEE Visualization and Graphics Technical FOR COMPUTER GRAPHICS Committee Conference Chair Enrico Gobbetti, CRS4, Italy Paper Co-Chairs Hamish Carr, Leeds University, UK Kwan-Liu Ma, UC Davis, USA Giuseppe Santucci, University of Rome “La Sapienza”, Italy STARs Chairs Rita Borgo, Swansea University, UK Fabio Ganovelli, ISTI-CNR, Italy Ivan Viola, Vienna University of Technology, Austria Short Papers Chairs Enrico Bertini, New York University, USA Jessie Kennedy, Edinburgh Napier University, UK Enrico Puppo, University of Genova, Italy Posters Chairs Ross Maciejewski, Arizona State University, USA Fabio Marton, CRS4, Italy DOI: 10.1111/cgf.12663 Eurographics Conference on Visualization (EuroVis) 2015 Vo l u me 3 4 (2015), Number 3 H. Carr, K.-L. Ma, and G. Santucci (Guest Editors) Sponsors Eurographics Conference on Visualization (EuroVis) 2015 Vo l u me 3 4 (2015), Number 3 H. Carr, K.-L. Ma, and G. Santucci (Guest Editors) International Programme Committee Aigner, Wolfgang, St. Poelten University of Applied Sciences, Austria Archambault, Daniel, Swansea University, United Kingdom Auber, David, University of Bordeaux, France Bak, Peter, IBM Research Lab, Israel Beyer, Johanna, Harvard University, United States Bruckner, Stefan, University of Bergen, Norway Chang, Remco, Tufts University, United States Chen, Jian, University of Maryland Baltimore County, United States Chiang, Yi-Jen, -

How Much Evaluation Is Enough? IEEE VIS 2013 Panel
Evaluation: How Much Evaluation is Enough? IEEE VIS 2013 Panel Organizer: Robert S Laramee, Swansea University, UK Panelists: Min Chen, Oxford University, UK David Ebert, Purdue University, US Brian Fisher, Simon Fraser University, Canada Tamara Munzner, University of British Columbia, Canada 1 INTRODUCTION evaluate a piece of visualization work? Most of us agree that evaluation is a critical aspect of Why this panel at VIS 2013? any visualization research paper. There are many This inspiring topic touches upon the experience and different aspects to the topic of evaluation including: sentiment of every researcher in visualization. It will performance-based such as evaluating computational form the basis of lively discussions that address speed and memory requirements. Other angles are these questions and perhaps more from the human-centered like user-studies, and domain expert audience. reviews to name a few examples. In order to demonstrate that a piece of visualization work yields 2 LOGISTICS a contribution, it must undergo some type of evaluation. The panelists will present their positions. The introductory remarks will be made by Bob Laramee. The peer-review process itself is a type of evaluation. His introduction will last for 5 minutes. Each panelist When we referee a research paper, we evaluate will be given 5-10 minutes, for a total of 25-45 whether or not the visualization work being described minutes of presentations. This will allow for has been evaluated adequately and appropriately. approximately 35-55 minutes of audience In an increasing number of cases papers are rejected participation in the discussion. All panelists will have based on what was judged, at that time, to contain an the opportunity to offer a summary view at the end of inadequate evaluation even though the technical or the panel (2 minutes each). -
Charles D. Hansen January 2, 2021
Vita Charles D. Hansen September 15, 2021 Current Address: School of Computing 50 S. Central Campus Drive, 3190 MEB, University of Utah Salt Lake City, Utah 84112 (801) 581-3154 (work) [email protected] email www.cs.utah.edu/˜hansen webpage Professional Employment 3/1/2019topresent UniversityofUtah DistinguishedProfessor of Computing 7/1 2005 to 3/1/2019 University of Utah Professor (School of Computing) 9/1/2003 to 6/20/2018 University of Utah Associate Director Scientific Computing and Imaging Institute 5/1 2012 to 06/30 2012 University of Stuttgart SimTech Senior Fellow 11/1 2011 to 04/30 2012 University Joseph Fourier Visiting Professor 7/1/2008 to 6/30/2010 University of Utah Associate Director School of Computing 8/15 2004 to 7/30 2005 INRIA Rhone-Alpes Visiting Scientist 9/1 1998 to 6/30 2005 University of Utah Associate Professor (School of Computing) 7/1 2001 to 6/03 2003 University of Utah Associate Director School of Computing 2/1 1997 to 8/31 1998 University of Utah Research Associate Professor (Dept. of Computer Science) 9/18 1989 to 1/31 1997 Los Alamos National Lab Technical Staff Member Advanced Computing Laboratory 9/1 1994 to 1/31 1997 Univ. of New Mexico Visiting Research Assistant Professor 9/1 1990 to 1/31 1997 New Mexico Tech Adjunct Professor 8/1 1988 to 7/31 1989: University of Utah Visiting Assistant Professor 7/5 1987 to 7/31 1988: INRIA Postdoctoral Research Scientist (Vision and Robotics) 1/1 1987 to 7/5 1987: University of Utah Research Assistant (Vision Group) 9/15 1986 to 12/31 1986: University of Utah Teaching Assistant (Computer Science Dept) 9/1 1986 to 9/14 1986: University of Utah Research Assistant (Vision Group) 9/1 1983 to 8/31 1986: ARO Research Fellow 6/16 1983 to 8/31 1983: University of Utah Research Assistant (Very Large Text Retrieval Project) 9/15 1982 to 6/15 1983: University of Utah Teaching Assistant (Computer Science Dept) 8/1 1979 to 8/31 1982 Fred P. -

Reflections on How Designers Design with Data
Reflections on How Designers Design With Data Alex Bigelow∗, Steven Druckery, Danyel Fishery, Miriah Meyer∗ ∗ University of Utah y Microsoft Research {abigelow, miriah}@cs.utah.edu {sdrucker, danyelf}@microsoft.com ABSTRACT of complex data, infographics [2,3,15] are a quickly emerging In recent years many popular data visualizations have emerged subclass of visualizations. These visualizations use static, vi- that are created largely by designers whose main area of ex- sual representations of data to tell a story or communicate pertise is not computer science. Designers generate these an idea, and have infiltrated the public space through a wide visualizations using a handful of design tools and environ- variety of sources, including news media, blogs, and art [38]. ments. To better inform the development of tools intended The increasing popularity of infographics has grown a for designers working with data, we set out to understand de- large community of people who create these visualizations. signers' challenges and perspectives. We interviewed profes- This community includes designers, artists, journalists, and sional designers, conducted observations of designers work- bloggers whose main expertise is not in engineering or pro- ing with data in the lab, and observed designers working gramming. These infographic designers tend to rely on soft- with data in team settings in the wild. A set of patterns ware illustration tools that ease the process of creating a emerged from these observations from which we extract a visual representation of data. number of themes that provide a new perspective on design considerations for visualization tool creators, as well as on known engineering problems.