Land Use Mapping of Malampuzha Dam Area Using Fuzzy C Means
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Online Seat Allotment - 2021 Department of Education Administration of UT of Lakshadweep
Online Seat Allotment - 2021 Department of Education Administration of UT of Lakshadweep College Wise Balance Seats Course Name College Name Total Seats Available Seats Ayurveda Nurse (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Ayurveda Pharmacist (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Ayurveda Therapist (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Craftmanship (One year) Institute of Hotel Management Catering Technology & Applied 10 0 Nutrition, Chennai Diploma in Civil Engineering Directorate of Technical Education, Guindy, Chennai 3 0 Diploma in Civil Engineering Govt. Polytechnic College, Kalamassery 3 0 Diploma in Civil Engineering Govt. Polytechnic College, Kozhikode 3 0 Diploma in Civil Engineering Training Institute, Gujarat 1 0 Diploma in Electrical & Directorate of Technical Education, Guindy, Chennai 11 0 Electronics Diploma in Electrical & Govt. Polytechnic College, Kalamassery 2 0 Electronics Diploma in Electrical & Govt. Polytechnic College, Kozhikode 2 0 Electronics Diploma in Electronics & Directorate of Technical Education, Guindy, Chennai 3 0 Communication Diploma in Electronics Engg. Govt. Polytechnic, Kannur 2 0 Diploma in Mechanical Engg. Directorate of Technical Education, Guindy, Chennai 9 0 Diploma in Mechanical Engg. Govt. Polytechnic College, Kalamassery 3 0 Diploma in Mechanical Engg. Govt. Polytechnic College, Kozhikode 2 0 Diploma in Printing Technology Training Institute, Gujarat 1 1 Electronics & Instruments Directorate of Technical Education, Guindy, Chennai 5 0 Shore Mechanic Course (SMC) Central Institute of Fisheries Nautical and Engineering 22 0 Training (CIFNET), Chennai Stenographer & Secretarial Govt. ITI, Chalakkudi 1 0 Assistant (English) Surveyor Govt. ITI, Chalakkudi 2 0 Electronics Mechanic Govt. ITI, Kalamassery 1 0 Electronics Mechanic Govt. -

Scheduled Caste Sub Plan (Scsp) 2014-15
Government of Kerala SCHEDULED CASTE SUB PLAN (SCSP) 2014-15 M iiF P A DC D14980 Directorate of Scheduled Caste Development Department Thiruvananthapuram April 2014 Planng^ , noD- documentation CONTENTS Page No; 1 Preface 3 2 Introduction 4 3 Budget Estimates 2014-15 5 4 Schemes of Scheduled Caste Development Department 10 5 Schemes implementing through Public Works Department 17 6 Schemes implementing through Local Bodies 18 . 7 Schemes implementing through Rural Development 19 Department 8 Special Central Assistance to Scheduled C ^te Sub Plan 20 9 100% Centrally Sponsored Schemes 21 10 50% Centrally Sponsored Schemes 24 11 Budget Speech 2014-15 26 12 Governor’s Address 2014-15 27 13 SCP Allocation to Local Bodies - District-wise 28 14 Thiruvananthapuram 29 15 Kollam 31 16 Pathanamthitta 33 17 Alappuzha 35 18 Kottayam 37 19 Idukki 39 20 Emakulam 41 21 Thrissur 44 22 Palakkad 47 23 Malappuram 50 24 Kozhikode 53 25 Wayanad 55 24 Kaimur 56 25 Kasaragod 58 26 Scheduled Caste Development Directorate 60 27 District SC development Offices 61 PREFACE The Planning Commission had approved the State Plan of Kerala for an outlay of Rs. 20,000.00 Crore for the year 2014-15. From the total State Plan, an outlay of Rs 1962.00 Crore has been earmarked for Scheduled Caste Sub Plan (SCSP), which is in proportion to the percentage of Scheduled Castes to the total population of the State. As we all know, the Scheduled Caste Sub Plan (SCSP) is aimed at (a) Economic development through beneficiary oriented programs for raising their income and creating assets; (b) Schemes for infrastructure development through provision of drinking water supply, link roads, house-sites, housing etc. -
List of Lacs with Local Body Segments (PDF
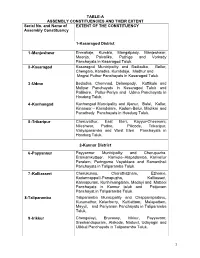
TABLE-A ASSEMBLY CONSTITUENCIES AND THEIR EXTENT Serial No. and Name of EXTENT OF THE CONSTITUENCY Assembly Constituency 1-Kasaragod District 1 -Manjeshwar Enmakaje, Kumbla, Mangalpady, Manjeshwar, Meenja, Paivalike, Puthige and Vorkady Panchayats in Kasaragod Taluk. 2 -Kasaragod Kasaragod Municipality and Badiadka, Bellur, Chengala, Karadka, Kumbdaje, Madhur and Mogral Puthur Panchayats in Kasaragod Taluk. 3 -Udma Bedadka, Chemnad, Delampady, Kuttikole and Muliyar Panchayats in Kasaragod Taluk and Pallikere, Pullur-Periya and Udma Panchayats in Hosdurg Taluk. 4 -Kanhangad Kanhangad Muncipality and Ajanur, Balal, Kallar, Kinanoor – Karindalam, Kodom-Belur, Madikai and Panathady Panchayats in Hosdurg Taluk. 5 -Trikaripur Cheruvathur, East Eleri, Kayyur-Cheemeni, Nileshwar, Padne, Pilicode, Trikaripur, Valiyaparamba and West Eleri Panchayats in Hosdurg Taluk. 2-Kannur District 6 -Payyannur Payyannur Municipality and Cherupuzha, Eramamkuttoor, Kankole–Alapadamba, Karivellur Peralam, Peringome Vayakkara and Ramanthali Panchayats in Taliparamba Taluk. 7 -Kalliasseri Cherukunnu, Cheruthazham, Ezhome, Kadannappalli-Panapuzha, Kalliasseri, Kannapuram, Kunhimangalam, Madayi and Mattool Panchayats in Kannur taluk and Pattuvam Panchayat in Taliparamba Taluk. 8-Taliparamba Taliparamba Municipality and Chapparapadavu, Kurumathur, Kolacherry, Kuttiattoor, Malapattam, Mayyil, and Pariyaram Panchayats in Taliparamba Taluk. 9 -Irikkur Chengalayi, Eruvassy, Irikkur, Payyavoor, Sreekandapuram, Alakode, Naduvil, Udayagiri and Ulikkal Panchayats in Taliparamba -

2004-05 - Term Loan
KERALA STATE BACKWARD CLASSES DEVELOPMENT CORPORATION LTD. A Govt. of Kerala Undertaking KSBCDC 2004-05 - Term Loan Name of Family Comm Gen R/ Project NMDFC Inst . Sl No. LoanNo Address Activity Sector Date Beneficiary Annual unity der U Cost Share No Income 010105768 Asha S R Keezhay Kunnathu Veedu,Irayam Codu,Cheriyakonni 0 F R Textile Business Sector 52632 44737 21/05/2004 2 010105770 Aswathy Sarath Tc/ 24/1074,Y.M.R Jn., Nandancodu,Kowdiar 0 F U Bakery Unit Business Sector 52632 44737 21/05/2004 2 010106290 Beena Kanjiramninna Veedu,Chowwera,Chowara Trivandrum 0 F R Readymade Business Sector 52632 44737 26/04/2004 2 010106299 Binu Kumar B Kunnuvila Veedu,Thozhukkal,Neyyattinkara 0 M U Dtp Centre Service Sector 52632 44737 22/04/2004 2 1 010106426 Satheesan Poovan Veedu, Tc 11/1823,Mavarthalakonam,Nalanchira 0 M U Cement Business Business Sector 52632 44737 19/04/2004 1 2 010106429 Chandrika Charuninnaveedu,Puthenkada,Thiruppuram 0 F R Copra Unit Business Sector 15789 13421 22/04/2004 1 3 010106430 Saji Shaji Bhavan,Mottamoola,Veeranakavu 0 M R Provision Store Business Sector 52632 44737 22/04/2004 1 4 010106431 Anil Kumar Varuvilakathu Pankaja Mandiram,Ooruttukala,Neyyattinkara 0 M R Timber Business Business Sector 52632 44737 22/04/2004 1 5 010106432 Satheesh Panavilacode Thekkarikath Veedu,Mullur,Mullur 0 M R Ready Made Garments Business Sector 52632 44737 22/04/2004 1 6 010106433 Raveendran R.S.Bhavan,Manthara,Perumpazhuthur 0 C M U Provision Store Business Sector 52632 44737 22/04/2004 1 010106433 Raveendran R.S.Bhavan,Manthara,Perumpazhuthur -

Panchayat/Municipality/Corp Oration
PMFBY List of Panchayats/Municipalities/Corporations proposed to be notified for Rabi II Plantain 2018-19 Season Insurance Unit Sl State District Taluka Block (Panchayat/Municipality/Corp Villages No oration) 1 Kerala Thiruvananthapuram Athiyannoor Kanjiramkulam All Villages in the Notified Panchayats 2 Kerala Thiruvananthapuram Athiyannoor Karimkulam All Villages in the Notified Panchayats 3 Kerala Thiruvananthapuram Athiyannoor Athiyanoor All Villages in the Notified Panchayats 4 Kerala Thiruvananthapuram Athiyannoor Kottukal All Villages in the Notified Panchayats 5 Kerala Thiruvananthapuram Athiyannoor Venganoor All Villages in the Notified Panchayats 6 Kerala Thiruvananthapuram Chirayinkeezhu Kizhuvilam All Villages in the Notified Panchayats 7 Kerala Thiruvananthapuram Chirayinkeezhu Mudakkal All Villages in the Notified Panchayats 8 Kerala Thiruvananthapuram Chirayinkeezhu Anjuthengu All Villages in the Notified Panchayats 9 Kerala Thiruvananthapuram Chirayinkeezhu Chirayinkeezhu All Villages in the Notified Panchayats 10 Kerala Thiruvananthapuram Chirayinkeezhu Kadakkavoor All Villages in the Notified Panchayats 11 Kerala Thiruvananthapuram Chirayinkeezhu Vakkom All Villages in the Notified Panchayats 12 Kerala Thiruvananthapuram Kilimanoor Madavoor All Villages in the Notified Panchayats 13 Kerala Thiruvananthapuram Kilimanoor Pallickal All Villages in the Notified Panchayats 14 Kerala Thiruvananthapuram Kilimanoor Kilimanoor All Villages in the Notified Panchayats 15 Kerala Thiruvananthapuram Kilimanoor Nagaroor All Villages -

12.02.2016 04.05.2016 31.01.2019 2 Online Ice Orange 23502.80
CONSENT DETAILS ISSUED FROM HEAD OFFICE ICE/ ICO/ Date of Date of Category & ICO(R) / Name and Capital Fee DD No & Date of Issue of No. Receipt of Type of Validity Registrtn/ Address investment remitted Date enquiry clearance/ VR industry Authoristn Refusal / Refusal M/s.UNITED BREWERIES LTD VARANAD P.O., 181.50 1 ONLINE ICE-EXP RED 60000/- 12.02.2016 04.05.2016 31.01.2019 CHERTHALA, LAKHS ALAPPUXHA- 688524 M/s PROPOSED TOWNSHIP PROJECT,MARKA Z KNOWLEDGE 006619,19.11 2 ONLINE ICE CITY,THUSHARA ORANGE 23502.80Lacs 490000/- 05.01.2016 04.04.2016 30.04.2018 .2015 GIRI ROAD, KAITHAPOYIL,K ODANCHERY(P.O ),KOZHIKODE- M/s SFC PLUS, GROUND FLOOR, CHALACHITHARA 554881,15.03 3 ONLINE ICO BHAVAN, ORANGE 620.74lacs 162500/- 29.03.16 21.04.2016 28.02.2019 VAZHUTHACAUD, .2016 THIRUVANANTH APURAM-695014 M/s APOLLO DIMORA APARTMENT CUM 001789,6.12. 4 ONLINE ICE ORANGE 2305lacs 180000/- 22.02.2016 02.05.2016 31.12.2018 HOTEL PROJECT 15 ,NELLIKODE,CAL ICUT, 673016 M/s PATSPIN INDIA LIMITED,PATODI 5 ONLINE ICO A NAGAR, PARA ORANGE 166.43Crores 480000/- 04.05.2016 30.06.2018 ROAD, KANJIKODE, PALAKKAD M/s. KAINAKARY BACKWATER RESORTS & HOTELS 617.58 6 ONLINE ICO ORANGE 50000/- 17.03.2016 25.04.2016 28.03.2019 (P) LTD, LAKHS KAINAKARI.P.O- 688013 OFFICE:RO, THIRUVANANTHAPURAM ICE/ ICO/ Date of Date of ICO(R) / Category & Capital Fee Issue of No. Name and Address Date of enquiry Validity receipt of VR Registrtn/ Type of industry investment remitted clearance/ Authoristn/ Refusal Refusal Snowman Logisitcs, Aroor, Cherthala, Orange 1 07.04.2016 ICE 30.01 crore -

Swami Dayananda AIM for Seva Chatralayam
Swami Dayananda AIM for Seva Chatralayam for Boys Student Strength: 35 ACADEMICS Overall, positive changes have been observed in our students with respect to studies, sports and participation in social activities. Many of our students come from poor backgrounds and lacked social skills and were poor in academics when they joined our hostel. Now, we have witnessed a huge improvement in their behaviour and outlook. CELEBRATIONS Independence Day celebrations saw flag hoisting in the hostel premises. During Founder’s Day celebrations, the hostelers and the staff reaffirmed their commitment to upholding our founder, Pujya Swami Dayananda Saraswati’s services to society through organisations like AIM for Seva. Festivals like Onam were also celebrated in the Chatralayam premises. SPORTS Republic Day saw flag hoisting and distribution of sweets. Festivals like Deepavali, Karthikai Deepam, Navaratri, Makkar Sankranti and Holi are all celebrated with equal fervour and they are always looked forward to by the students. WELFARE Our students regularly attend NSS (National Service Scheme) camps as well as seminars organised by the child welfare department. VOLUNTEER Kerala (Chatralayam - Palakkad) A volunteer group of NRIs aims to help develop musical talent in the students through the Karoke Insta Gana. SUSTAINABLE LIVING A well-constructed goshala houses 25 cows from where the hostel gets its daily requirement of milk. The hostel has a large vegetable garden with seasonal plants and various types of plantains. TRIPS The students were taken on a trip to the Ramaeshwaram temple, beach in Madurai, and to the Thiruparankundram, Pazhamudhircholai, Pillayarpati and Pazhani temples, besides an outing to Malampuzha dam gardens, Palakkad fort and Kakapathri car festival. -

Report of Rapid Impact Assessment of Flood/ Landslides on Biodiversity Focus on Community Perspectives of the Affect on Biodiversity and Ecosystems
IMPACT OF FLOOD/ LANDSLIDES ON BIODIVERSITY COMMUNITY PERSPECTIVES AUGUST 2018 KERALA state BIODIVERSITY board 1 IMPACT OF FLOOD/LANDSLIDES ON BIODIVERSITY - COMMUnity Perspectives August 2018 Editor in Chief Dr S.C. Joshi IFS (Retd) Chairman, Kerala State Biodiversity Board, Thiruvananthapuram Editorial team Dr. V. Balakrishnan Member Secretary, Kerala State Biodiversity Board Dr. Preetha N. Mrs. Mithrambika N. B. Dr. Baiju Lal B. Dr .Pradeep S. Dr . Suresh T. Mrs. Sunitha Menon Typography : Mrs. Ajmi U.R. Design: Shinelal Published by Kerala State Biodiversity Board, Thiruvananthapuram 2 FOREWORD Kerala is the only state in India where Biodiversity Management Committees (BMC) has been constituted in all Panchayats, Municipalities and Corporation way back in 2012. The BMCs of Kerala has also been declared as Environmental watch groups by the Government of Kerala vide GO No 04/13/Envt dated 13.05.2013. In Kerala after the devastating natural disasters of August 2018 Post Disaster Needs Assessment ( PDNA) has been conducted officially by international organizations. The present report of Rapid Impact Assessment of flood/ landslides on Biodiversity focus on community perspectives of the affect on Biodiversity and Ecosystems. It is for the first time in India that such an assessment of impact of natural disasters on Biodiversity was conducted at LSG level and it is a collaborative effort of BMC and Kerala State Biodiversity Board (KSBB). More importantly each of the 187 BMCs who were involved had also outlined the major causes for such an impact as perceived by them and suggested strategies for biodiversity conservation at local level. Being a study conducted by local community all efforts has been made to incorporate practical approaches for prioritizing areas for biodiversity conservation which can be implemented at local level. -

Multi Village Piped Water Supply Scheme
MULTI VILLAGE PIPED WATER SUPPLY SCHEME LAKKIDIPERUR PALAKKAD, KERALA September 2020 MULTI VILLAGE PIPED WATER SUPPLY LAKKIDIPERUR PALAKKAD, KERALA In Kerala, almost 67% of the population Lakkidiperur GP was implemented under depends on open wells, borewells, and the complete supervision of the other traditional water sources for Government of Kerala as per the drinking water at present. The organised objectives of the World Bank which funded water supply system under the Kerala the Jalanidhi project. At this point, the Water Authority (KWA) and Kerala Rural MVPWS is managed by the Scheme Level Water Supply and Sanitation Agency Committee (SLC), the apex institution. The (KRWSA/Jalanidhi) provides safe water 39 Beneficiary Groups (BGs) under the access to the rest (33%) of the population. scheme have a common system with a The new initiative by the Government of water source, pumping system, pumping India through the Jal Jeevan Mission, main, piped water supply and purification launched in the year 2020, envisages plant, water storage tank, and water filling this gap by providing household pumping distribution network. There are pipe water supply to all rural households no stand posts in the area under the by 2024 with a focus on small scale scheme. The alternative sources to fetch community-managed water supply water during disruptions are individual schemes and an emphasis on source dug wells. sustainability. Profile of beneficiary Piped water supply scheme: households Location, water source and There are 39 registered BGs as legal scheme details entities in the MVPWS scheme covering 13 Lakkidiperur gram panchayat (GP) in of the total 19 wards of Lakkidiperur GP. -

Aquaculture Asia April 2008.Indd
Research & farming techniques zone. Proceedings of the toward further Petchkamnerd, J., Suanrattanachai, P. and Tantong, A. (1986). Kumatibai kodmaiwad- development of coastal resource management: Auimrod, S. (2003). Coordination between uaykarnpramong (pak 3) waduay muad 4 Lessons gained through locally based coastal crab trap and crab gill nets fi sheries: change satikanpramong, muad 5 kankuabkum, muad 6 resource management in Pathew District, and adjustment of fi shing gear for responsible botkamnodetos promduay kodmai lae rabaeb Chumphon Province, Thailand. TD/RP/58, fi sheries project to contribute to locally based thi samkan thi keawkub kanpramong, Law LBCRM-PD No. 23. pp. 105-112 coastal resource management, Proceedings section, Control and extension division, the Suanrattanachai, P., Petchkamnerd, P. and of the “Toward further development of coastal Department of Fisheries, Ministry of Agriculture Auimrod, S. (2003). Experience in the Zoning of resource management: Lessons gained through and Cooperatives no. 2/1986 (2529) (in Thai). fi sh cage and shellfi sh culture areas. Proceed- locally based coastal resource management in Rajachagool, C. Tambol administrative organiza- ings of the “Toward further development of Pathew District, Chumphon Province, Thailand.” tion: are the people in the dramatis personae coastal resource management: Lessons gained TD/RP/58, LBCRM-PD No. 23, pp.123-130. or in the audience? at www.unescap. through locally based coastal resource manage- Bureau Offi ce of Fisheries Administration and org/ttdw/Publications/TPTS_pubs/TxBul- ment in Pathew District, Chumphon Province, Management (2003). Ruamkod mai keawkub letin_69/bulletin69_b.pdf. Thailand.” TD/RP/58, LBCRM-PD No. 23. pp. kanpramong, the Department of Fisherires, 113-122 Ministry of Agriculture and Cooperatives (in The World Humanity Action Trust. -

Centre for Development Studies on MDM for the State of Kerala for the Period: 1St April to 31St September 2012
Fourth Half Yearly Monitoring Report of Centre for Development Studies on MDM for the State of Kerala for the Period: 1st April to 31st September 2012 DISTRICTS COVERED Thrissur Wayanad Palakkad Malappuram Pathanamthitta 2012 1 Contents Section Title Page Preface 3 I General information 5 II Consolidated report on Thrissur district 8 III Consolidated report on Wayanad district 19 IV Consolidated report on Palakkad district 28 V Consolidated report on Malappuram 38 VI Consolidated report on Pathanamthitta 47 VII Summary report 57 2 Preface The school lunch programme has been in operation in different parts of India since 1925. However its coverage has been limited. It has covered only a small portion of the poor children in several states. The total coverage has been about 13 million children in the country in 1978. This has increased to 17 million by the end of 1983. Further there has been no uniformity in organization of school lunch in most of the states. In some states the programme has been limited to certain districts. The school lunch programme has been initiated in Kerala in 1941. The operation of this scheme has spread to all schools by the year 1961-62. Under the scheme, rice or wheat kanji has been given to the children at noon. The present school lunch programme is called Midday Meal Programme (MDM) launched by the Government of India in all states. Under this programme, the entire cost of food grains supplied by the FCI, the cost of transportation of food grains from the godowns of FCI to the schools and the expenditure involved in management, monitoring and evaluation of the scheme are borne by government of India. -

Industry Linkage
Name of the partnering institution/ industry Year of Duration Sl No. Title of the linkage Nature of linkage /research lab with contact details commencement From To 2018-2019 Geodesic Techniques Pvt. Ltd., Bengaluru, Internship & 1 Industrial Training 2018 6/1/2018 5/31/2019 Karnataka 560058 Project Work LPSC-ISRO, Valiamala, Thiruvananthapuram, Kerala Internship & 2 Industrial Training 2018 6/1/2018 5/31/2019 695547 Project Work WVA Consulting Engineers Pvt. Ltd., Kolencherry, 3 Industrial Training 2019 1/14/2019 2/1/2019 Internship Ernakulam Kerala, 682311 Internship & 4 Industrial Training KITCO, Vennala, Kochi, Kerala 682028 2018 6/1/2018 5/31/2019 Project Work VSSC-ISRO, Kochuveli, Thiruvananthapuram, Kerala Internship & 5 Industrial Training 2018 6/1/2018 5/31/2019 695022 Project Work VMware Software India Pvt. Ltd., J. P. Nagar, Bengaluru, 6 Industrial Training 2019 7/8/2019 7/12/2019 Internship Karnataka 560076 7 Industrial Training Keltron Controls, Aroor, Alappuzha, Kerala 688534 2019 7/4/2019 7/11/2019 Internship Cochin Shipyard Limited, Ravipuram, Perumanoor, 8 Industrial Training 2019 7/1/2019 7/6/2019 Internship Kochi, Kerala 682015 Torc infotech, Bypass Junction, Ponekkara, Edappally, 9 Industrial Training 2019 7/11/2019 7/15/2019 Internship Kochi, Kerala 682024 10 Industrial Training Pantech ProEd Pvt.Ltd, Ernakulam, Kerala 682017 2019 7/11/2019 7/15/2019 Internship Kerala Electrical and Allied Engineering Company 11 Industrial Training 2019 7/10/2019 7/15/2019 Internship Limited, Mamala, Kochi 682305 Al Aflaj Building