A Topological Disk in a 4-Manifold Can Be Approximated by Piecewise Linear Disks by Gerard A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Simple Infinite Presentations for the Mapping Class Group of a Compact
SIMPLE INFINITE PRESENTATIONS FOR THE MAPPING CLASS GROUP OF A COMPACT NON-ORIENTABLE SURFACE RYOMA KOBAYASHI Abstract. Omori and the author [6] have given an infinite presentation for the mapping class group of a compact non-orientable surface. In this paper, we give more simple infinite presentations for this group. 1. Introduction For g ≥ 1 and n ≥ 0, we denote by Ng,n the closure of a surface obtained by removing disjoint n disks from a connected sum of g real projective planes, and call this surface a compact non-orientable surface of genus g with n boundary components. We can regard Ng,n as a surface obtained by attaching g M¨obius bands to g boundary components of a sphere with g + n boundary components, as shown in Figure 1. We call these attached M¨obius bands crosscaps. Figure 1. A model of a non-orientable surface Ng,n. The mapping class group M(Ng,n) of Ng,n is defined as the group consisting of isotopy classes of all diffeomorphisms of Ng,n which fix the boundary point- wise. M(N1,0) and M(N1,1) are trivial (see [2]). Finite presentations for M(N2,0), M(N2,1), M(N3,0) and M(N4,0) ware given by [9], [1], [14] and [16] respectively. Paris-Szepietowski [13] gave a finite presentation of M(Ng,n) with Dehn twists and arXiv:2009.02843v1 [math.GT] 7 Sep 2020 crosscap transpositions for g + n > 3 with n ≤ 1. Stukow [15] gave another finite presentation of M(Ng,n) with Dehn twists and one crosscap slide for g + n > 3 with n ≤ 1, applying Tietze transformations for the presentation of M(Ng,n) given in [13]. -

An Introduction to Topology the Classification Theorem for Surfaces by E
An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5. -

1 University of California, Berkeley Physics 7A, Section 1, Spring 2009
1 University of California, Berkeley Physics 7A, Section 1, Spring 2009 (Yury Kolomensky) SOLUTIONS TO THE SECOND MIDTERM Maximum score: 100 points 1. (10 points) Blitz (a) hoop, disk, sphere This is a set of simple questions to warm you up. The (b) disk, hoop, sphere problem consists of five questions, 2 points each. (c) sphere, hoop, disk 1. Circle correct answer. Imagine a basketball bouncing on a court. After a dozen or so (d) sphere, disk, hoop bounces, the ball stops. From this, you can con- (e) hoop, sphere, disk clude that Answer: (d). The object with highest moment of (a) Energy is not conserved. inertia has the largest kinetic energy at the bot- (b) Mechanical energy is conserved, but only tom, and would reach highest elevation. The ob- for a single bounce. ject with the smallest moment of inertia (sphere) (c) Total energy in conserved, but mechanical will therefore reach lowest altitude, and the ob- energy is transformed into other types of ject with the largest moment of inertia (hoop) energy (e.g. heat). will be highest. (d) Potential energy is transformed into kinetic 4. A particle attached to the end of a massless rod energy of length R is rotating counter-clockwise in the (e) None of the above. horizontal plane with a constant angular velocity ω as shown in the picture below. Answer: (c) 2. Circle correct answer. In an elastic collision ω (a) momentum is not conserved but kinetic en- ergy is conserved; (b) momentum is conserved but kinetic energy R is not conserved; (c) both momentum and kinetic energy are conserved; (d) neither kinetic energy nor momentum is Which direction does the vector ~ω point ? conserved; (e) none of the above. -

The Geometry of the Disk Complex
JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 26, Number 1, January 2013, Pages 1–62 S 0894-0347(2012)00742-5 Article electronically published on August 22, 2012 THE GEOMETRY OF THE DISK COMPLEX HOWARD MASUR AND SAUL SCHLEIMER Contents 1. Introduction 1 2. Background on complexes 3 3. Background on coarse geometry 6 4. Natural maps 8 5. Holes in general and the lower bound on distance 11 6. Holes for the non-orientable surface 13 7. Holes for the arc complex 14 8. Background on three-manifolds 14 9. Holes for the disk complex 18 10. Holes for the disk complex – annuli 19 11. Holes for the disk complex – compressible 22 12. Holes for the disk complex – incompressible 25 13. Axioms for combinatorial complexes 30 14. Partition and the upper bound on distance 32 15. Background on Teichm¨uller space 41 16. Paths for the non-orientable surface 44 17. Paths for the arc complex 47 18. Background on train tracks 48 19. Paths for the disk complex 50 20. Hyperbolicity 53 21. Coarsely computing Hempel distance 57 Acknowledgments 60 References 60 1. Introduction Suppose M is a compact, connected, orientable, irreducible three-manifold. Sup- pose S is a compact, connected subsurface of ∂M so that no component of ∂S bounds a disk in M. In this paper we study the intrinsic geometry of the disk complex D(M,S). The disk complex has a natural simplicial inclusion into the curve complex C(S). Surprisingly, this inclusion is generally not a quasi-isometric embedding; there are disks which are close in the curve complex yet far apart in the disk complex. -

Recognizing Surfaces
RECOGNIZING SURFACES Ivo Nikolov and Alexandru I. Suciu Mathematics Department College of Arts and Sciences Northeastern University Abstract The subject of this poster is the interplay between the topology and the combinatorics of surfaces. The main problem of Topology is to classify spaces up to continuous deformations, known as homeomorphisms. Under certain conditions, topological invariants that capture qualitative and quantitative properties of spaces lead to the enumeration of homeomorphism types. Surfaces are some of the simplest, yet most interesting topological objects. The poster focuses on the main topological invariants of two-dimensional manifolds—orientability, number of boundary components, genus, and Euler characteristic—and how these invariants solve the classification problem for compact surfaces. The poster introduces a Java applet that was written in Fall, 1998 as a class project for a Topology I course. It implements an algorithm that determines the homeomorphism type of a closed surface from a combinatorial description as a polygon with edges identified in pairs. The input for the applet is a string of integers, encoding the edge identifications. The output of the applet consists of three topological invariants that completely classify the resulting surface. Topology of Surfaces Topology is the abstraction of certain geometrical ideas, such as continuity and closeness. Roughly speaking, topol- ogy is the exploration of manifolds, and of the properties that remain invariant under continuous, invertible transforma- tions, known as homeomorphisms. The basic problem is to classify manifolds according to homeomorphism type. In higher dimensions, this is an impossible task, but, in low di- mensions, it can be done. Surfaces are some of the simplest, yet most interesting topological objects. -

The Real Projective Spaces in Homotopy Type Theory
The real projective spaces in homotopy type theory Ulrik Buchholtz Egbert Rijke Technische Universität Darmstadt Carnegie Mellon University Email: [email protected] Email: [email protected] Abstract—Homotopy type theory is a version of Martin- topology and homotopy theory developed in homotopy Löf type theory taking advantage of its homotopical models. type theory (homotopy groups, including the fundamen- In particular, we can use and construct objects of homotopy tal group of the circle, the Hopf fibration, the Freuden- theory and reason about them using higher inductive types. In this article, we construct the real projective spaces, key thal suspension theorem and the van Kampen theorem, players in homotopy theory, as certain higher inductive types for example). Here we give an elementary construction in homotopy type theory. The classical definition of RPn, in homotopy type theory of the real projective spaces as the quotient space identifying antipodal points of the RPn and we develop some of their basic properties. n-sphere, does not translate directly to homotopy type theory. R n In classical homotopy theory the real projective space Instead, we define P by induction on n simultaneously n with its tautological bundle of 2-element sets. As the base RP is either defined as the space of lines through the + case, we take RP−1 to be the empty type. In the inductive origin in Rn 1 or as the quotient by the antipodal action step, we take RPn+1 to be the mapping cone of the projection of the 2-element group on the sphere Sn [4]. -

On Generalizing Boy's Surface: Constructing a Generator of the Third Stable Stem
TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 298. Number 1. November 1986 ON GENERALIZING BOY'S SURFACE: CONSTRUCTING A GENERATOR OF THE THIRD STABLE STEM J. SCOTT CARTER ABSTRACT. An analysis of Boy's immersion of the projective plane in 3-space is given via a collection of planar figures. An analogous construction yields an immersion of the 3-sphere in 4-space which represents a generator of the third stable stem. This immersion has one quadruple point and a closed curve of triple points whose normal matrix is a 3-cycle. Thus the corresponding multiple point invariants do not vanish. The construction is given by way of a family of three dimensional cross sections. Stable homotopy groups can be interpreted as bordism groups of immersions. The isomorphism between such groups is given by the Pontryagin-Thorn construction on the normal bundle of representative immersions. The self-intersection sets of im- mersed n-manifolds in Rn+l provide stable homotopy invariants. For example, Boy's immersion of the projective plane in 3-space represents a generator of II3(POO); this can be seen by examining the double point set. In this paper a direct analog of Boy's surface is constructed. This is an immersion of S3 in 4-space which represents a generator of II]; the self-intersection data of this immersion are as simple as possible. It may be that appropriate generalizations of this construction will exem- plify a nontrivial Kervaire invariant in dimension 30, 62, and so forth. I. Background. Let i: M n 'T-+ Rn+l denote a general position immersion of a closed n-manifold into real (n + I)-space. -

Surfaces and Complex Analysis (Lecture 34)
Surfaces and Complex Analysis (Lecture 34) May 3, 2009 Let Σ be a smooth surface. We have seen that Σ admits a conformal structure (which is unique up to a contractible space of choices). If Σ is oriented, then a conformal structure on Σ allows us to view Σ as a Riemann surface: that is, as a 1-dimensional complex manifold. In this lecture, we will exploit this fact together with the following important fact from complex analysis: Theorem 1 (Riemann uniformization). Let Σ be a simply connected Riemann surface. Then Σ is biholo- morphic to one of the following: (i) The Riemann sphere CP1. (ii) The complex plane C. (iii) The open unit disk D = fz 2 C : z < 1g. If Σ is an arbitrary surface, then we can choose a conformal structure on Σ. The universal cover Σb then inherits the structure of a simply connected Riemann surface, which falls into the classification of Theorem 1. We can then recover Σ as the quotient Σb=Γ, where Γ ' π1Σ is a group which acts freely on Σb by holmorphic maps (if Σ is orientable) or holomorphic and antiholomorphic maps (if Σ is nonorientable). For simplicity, we will consider only the orientable case. 1 If Σb ' CP , then the group Γ must be trivial: every orientation preserving automorphism of S2 has a fixed point (by the Lefschetz trace formula). Because Γ acts freely, we must have Γ ' 0, so that Σ ' S2. To see what happens in the other two cases, we need to understand the holomorphic automorphisms of C and D. -

Black Hole Accretion Torus & Magnetic Fields
Proceedings of RAGtime ?/?, ?{?/?{? September, ????/????, Opava, Czech Republic 1 S. Hled´ıkand Z. Stuchl´ık,editors, Silesian University in Opava, ????, pp. 1{11 Simulations of black hole accretion torus in various magnetic field configurations Martin Koloˇs,1,a and Agnieszka Janiuk,2,b 1 Research Centre for Theoretical Physics and Astrophysics, Institute of Physics , Silesian University in Opava, Bezruˇcovo n´am.13,CZ-74601 Opava, Czech Republic 2 Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikow 32/46, 02-668 Warsaw, Poland [email protected] [email protected] ABSTRACT Using axisymetric general relativistic magnetohydrodynamics simulations we study evolution of accretion torus around black hole endowed with dif- ferent initial magnetic field configurations. Due to accretion of material onto black hole, parabolic magnetic field will develop in accretion torus funnel around vertical axis, for any initial magnetic field configuration. Keywords: GRMHD simulation { accretion { black hole { magnetic field 1 INTRODUCTION There are two long range forces in physics: gravity and electromagnetism (EM) and both of these forces are crucial for proper description of high energetic processes around black holes (BHs). In realistic astrophysical situations the EM field around BH a is not strong enough (< 1018 Gs) to really contribute to spacetime curvature andarXiv:2004.07535v1 [astro-ph.HE] 16 Apr 2020 rotating BH can be fully described by standard Kerr metric spacetime. Hence the EM field and matter orbiting around central BH can be considered just as test fields in axially symmetric Kerr spacetime background. While the distribution of matter around central BH can be well described by thin Keplerian accretion disk or thick accretion torus, the exact shape of EM field around BH, i.e. -

Brouwer's Fixed Point Theorem
BROUWER'S FIXED POINT THEOREM JASPER DEANTONIO Abstract. In this paper we prove Brouwer's Fixed Point Theorem, which states that for any continuous transformation f : D ! D of any figure topo- logically equivalent to the closed disk, there exists a point p such that f(p) = p. Contents 1. Introduction and Definition of Basic Terms 1 2. Constructing a Sperner Labeling and Proving Sperner's Lemma 2 3. Proof of Brouwer's Fixed Point Theorem 4 Acknowledgments 5 References 5 1. Introduction and Definition of Basic Terms This paper presents the proof of Brouwer's Fixed Point Theorem, which states that for any continuous transformation f : D ! D of the closed disk D = fp 2 R2 : jjpjj ≤ 1g, there exists a point p such that f(p) = p. In fact, we prove that this is true for the cell, that is, any figure homeomorphic to D. Before we prove this theorem, we present definitions. Definition 1.1. Let f be a continuous transformation of a set D into itself. A fixed point of f is a point p such that f(p) = p. Definition 1.2. If, for every continuous transformation f : D ! D, there exists a point p such that f(p) = p, then D has the fixed point property. These definitions allow us to restate Brouwer's Fixed Point Theorem in a much simpler manner: Theorem 1.3 (Brouwer's Fixed Point Theorem). Cells have the fixed point prop- erty. We want to show that for any continuous transformation f : D ! D of any figure topologically equivalent to the closed disk, there exists a point p such that f(p) = p. -

On the Axisymmetric Loading of an Annular Crack by a Disk Inclusion
Journal of Engineering Mathematics 46: 377–393, 2003. © 2003 Kluwer Academic Publishers. Printed in the Netherlands. On the axisymmetric loading of an annular crack by a disk inclusion A. P. S. SELVADURAI Department of Civil Engineering and Applied Mechanics, McGill University, 817 Sherbrooke Street West, Montréal, QC, Canada, H3A 2K6 (E-mail: [email protected]) Received 31 May 2002; accepted in revised form 10 March 2003 Abstract. This paper examines the axisymmetric elastostatic problem related to the loading of an annular crack by a rigid disk-shaped inclusion subjected to a central force. The integral equations associated with the resulting mixed-boundary-value problem are solved numerically to determine the load-displacement result for the rigid inclusion and the Mode II stress-intensity factors at the boundaries of the annular crack. The results presented are applicable to a wide range of Poisson’s ratios ranging from zero to one half. Key words: annular crack, crack-inclusion interaction, inclusion problem, three-part boundary-value problem, triple integral equations 1. Introduction The annular crack represents an idealized form of a flattened toroidal crack, which has been investigated quite extensively in connection with problems in fracture mechanics. The annular crack also represents a general case from which solutions to both penny-shaped cracks and external circular cracks can be recovered as special cases (see e.g., Sneddon and Lowengrub [1, Chapter 3]; Kassir and Sih [2, Chapter 1]; Cherepanov [3, Appendix A]). The axisymmetric annular-crack problem examined by Grinchenko and Ulitko [4] is based on an approximate solution of the governing equations. -
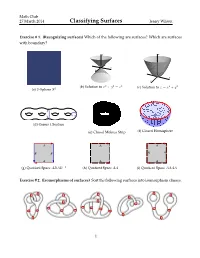
Classifying Surfaces Jenny Wilson
Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Exercise # 1. (Recognizing surfaces) Which of the following are surfaces? Which are surfaces with boundary? z z y x y x (b) Solution to x2 + y2 = z2 (c) Solution to z = x2 + y2 (a) 2–Sphere S2 (d) Genus 4 Surface (e) Closed Mobius Strip (f) Closed Hemisphere A A A BB A A A A A (g) Quotient Space ABAB−1 (h) Quotient Space AA (i) Quotient Space AAAA Exercise # 2. (Isomorphisms of surfaces) Sort the following surfaces into isomorphism classes. 1 Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Exercise # 3. (Quotient surfaces) Identify among the following quotient spaces: a cylinder, a Mobius¨ band, a sphere, a torus, real projective space, and a Klein bottle. A A A A BB A B BB A A B A Exercise # 4. (Gluing Mobius bands) How many boundary components does a Mobius band have? What surface do you get by gluing two Mobius bands along their boundary compo- nents? Exercise # 5. (More quotient surfaces) Identify the following surfaces. A A BB A A h h g g Triangulations Exercise # 6. (Minimal triangulations) What is the minimum number of triangles needed to triangulate a sphere? A cylinder? A torus? 2 Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Orientability Exercise # 7. (Orientability is well-defined) Fix a surface S. Prove that if one triangulation of S is orientable, then all triangulations of S are orientable. Exercise # 8. (Orientability) Prove that the disk, sphere, and torus are orientable. Prove that the Mobius strip and Klein bottle are nonorientiable.