Polynomial Division by Convolution"
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Algebra II Level 1
Algebra II 5 credits – Level I Grades: 10-11, Level: I Prerequisite: Minimum grade of 70 in Geometry Level I (or a minimum grade of 90 in Geometry Topics) Units of study include: equations and inequalities, linear equations and functions, systems of linear equations and inequalities, matrices and determinants, quadratic functions, polynomials and polynomial functions, powers, roots, and radicals, rational equations and functions, sequence and series, and probability and statistics. PROFICIENCIES INEQUALITIES -Solve inequalities -Solve combined inequalities -Use inequality models to solve problems -Solve absolute values in open sentences -Solve absolute value sentences graphically LINEAR EQUATION FUNCTIONS -Solve open sentences in two variables -Graph linear equations in two variables -Find the slope of the line -Write the equation of a line -Solve systems of linear equations in two variables -Apply systems of equations to solve real word problems -Solve linear inequalities in two variables -Find values of functions and graphs -Find equations of linear functions and apply properties of linear functions -Graph relations and determine when relations are functions PRODUCTS AND FACTORS OF POLYNOMIALS -Simplify, add and subtract polynomials -Use laws of exponents to multiply a polynomial by a monomial -Calculate the product of two or more polynomials -Demonstrate factoring -Solve polynomial equations and inequalities -Apply polynomial equations to solve real world problems RATIONAL EQUATIONS -Simplify quotients using laws of exponents -Simplify -

The Computational Complexity of Polynomial Factorization
Open Questions From AIM Workshop: The Computational Complexity of Polynomial Factorization 1 Dense Polynomials in Fq[x] 1.1 Open Questions 1. Is there a deterministic algorithm that is polynomial time in n and log(q)? State of the art algorithm should be seen on May 16th as a talk. 2. How quickly can we factor x2−a without hypotheses (Qi Cheng's question) 1 State of the art algorithm Burgess O(p 2e ) 1.2 Open Question What is the exponent of the probabilistic complexity (for q = 2)? 1.3 Open Question Given a set of polynomials with very low degree (2 or 3), decide if all of them factor into linear factors. Is it faster to do this by factoring their product or each one individually? (Tanja Lange's question) 2 Sparse Polynomials in Fq[x] 2.1 Open Question α β Decide whether a trinomial x + ax + b with 0 < β < α ≤ q − 1, a; b 2 Fq has a root in Fq, in polynomial time (in log(q)). (Erich Kaltofen's Question) 2.2 Open Questions 1. Finding better certificates for irreducibility (a) Are there certificates for irreducibility that one can verify faster than the existing irreducibility tests? (Victor Miller's Question) (b) Can you exhibit families of sparse polynomials for which you can find shorter certificates? 2. Find a polynomial-time algorithm in log(q) , where q = pn, that solves n−1 pi+pj n−1 pi Pi;j=0 ai;j x +Pi=0 bix +c in Fq (or shows no solutions) and works 1 for poly of the inputs, and never lies. -

Section P.2 Solving Equations Important Vocabulary
Section P.2 Solving Equations 5 Course Number Section P.2 Solving Equations Instructor Objective: In this lesson you learned how to solve linear and nonlinear equations. Date Important Vocabulary Define each term or concept. Equation A statement, usually involving x, that two algebraic expressions are equal. Extraneous solution A solution that does not satisfy the original equation. Quadratic equation An equation in x that can be written in the general form 2 ax + bx + c = 0 where a, b, and c are real numbers with a ¹ 0. I. Equations and Solutions of Equations (Page 12) What you should learn How to identify different To solve an equation in x means to . find all the values of x types of equations for which the solution is true. The values of x for which the equation is true are called its solutions . An identity is . an equation that is true for every real number in the domain of the variable. A conditional equation is . an equation that is true for just some (or even none) of the real numbers in the domain of the variable. II. Linear Equations in One Variable (Pages 12-14) What you should learn A linear equation in one variable x is an equation that can be How to solve linear equations in one variable written in the standard form ax + b = 0 , where a and b and equations that lead to are real numbers with a ¹ 0 . linear equations A linear equation has exactly one solution(s). To solve a conditional equation in x, . isolate x on one side of the equation by a sequence of equivalent, and usually simpler, equations, each having the same solution(s) as the original equation. -

Vocabulary Eighth Grade Math Module Four Linear Equations
VOCABULARY EIGHTH GRADE MATH MODULE FOUR LINEAR EQUATIONS Coefficient: A number used to multiply a variable. Example: 6z means 6 times z, and "z" is a variable, so 6 is a coefficient. Equation: An equation is a statement about equality between two expressions. If the expression on the left side of the equal sign has the same value as the expression on the right side of the equal sign, then you have a true equation. Like Terms: Terms whose variables and their exponents are the same. Example: 7x and 2x are like terms because the variables are both “x”. But 7x and 7ͬͦ are NOT like terms because the x’s don’t have the same exponent. Linear Expression: An expression that contains a variable raised to the first power Solution: A solution of a linear equation in ͬ is a number, such that when all instances of ͬ are replaced with the number, the left side will equal the right side. Term: In Algebra a term is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or − signs Unit Rate: A unit rate describes how many units of the first type of quantity correspond to one unit of the second type of quantity. Some common unit rates are miles per hour, cost per item & earnings per week Variable: A symbol for a number we don't know yet. It is usually a letter like x or y. Example: in x + 2 = 6, x is the variable. Average Speed: Average speed is found by taking the total distance traveled in a given time interval, divided by the time interval. -

The Evolution of Equation-Solving: Linear, Quadratic, and Cubic
California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work. -

2.3 Solving Linear Equations a Linear Equation Is an Equation in Which All Variables Are Raised to Only the 1 Power. in This
2.3 Solving Linear Equations A linear equation is an equation in which all variables are raised to only the 1st power. In this section, we review the algebra of solving basic linear equations, see how these skills can be used in applied settings, look at linear equations with more than one variable, and then use this to find inverse functions of a linear function. Basic Linear Equations To solve a basic linear equation in one variable we use the basic operations of +, -, ´, ¸ to isolate the variable. Example 1 Solve each of the following: (a) 2x + 4 = 5x -12 (b) 3(2x - 4) = 2(x + 5) Applied Problems Example 2 Company A charges a monthly fee of $5.00 plus 99 cents per download for songs. Company B charges a monthly fee of $7.00 plus 79 cents per download for songs. (a) Give a formula for the monthly cost with each of these companies. (b) For what number of downloads will the monthly cost be the same for both companies? Example 3 A small business is considering hiring a new sales rep. to market its product in a nearby city. Two pay scales are under consideration. Pay Scale 1 Pay the sales rep. a base yearly salary of $10000 plus a commission of 8% of the total yearly sales. Pay Scale 2 Pay the sales rep a base yearly salary of $13000 plus a commission of 6% of the total yearly sales. (a) For each scale above, give a function formula to express the total yearly earnings as a function of the total yearly sales. -

Analysis of XSL Applied to BES
Analysis of XSL Applied to BES By: Lim Chu Wee, Khoo Khoong Ming. History (2002) Courtois and Pieprzyk announced a plausible attack (XSL) on Rijndael AES. Complexity of ≈ 2225 for AES-256. Later Murphy and Robshaw proposed embedding AES into BES, with equations over F256. S-boxes involved fewer monomials, and would provide a speedup for XSL if it worked (287 for AES-128 in best case). Murphy and Robshaw also believed XSL would not work. (Asiacrypt 2005) Cid and Leurent showed that “compact XSL” does not crack AES. Summary of Our Results We analysed the application of XSL on BES. Concluded: the estimate of 287 was too optimistic; we obtained a complexity ≥ 2401, even if XSL works. Hence it does not crack BES-128. Found further linear dependencies in the expanded equations, upon applying XSL to BES. Similar dependencies exist for AES – unaccounted for in computations of Courtois and Pieprzyk. Open question: does XSL work at all, for some P? Quick Description of AES & BES AES Structure Very general description of AES (in F256): Input: key (k0k1…ks-1), message (M0M1…M15). Suppose we have aux variables: v0, v1, …. At each step we can do one of three things: Let vi be an F2-linear map T of some previously defined byte: one of the vj’s, kj’s or Mj’s. Let vi = XOR of two bytes. Let vi = S(some byte). Here S is given by the map: x → x-1 (S(0)=0). Output = 16 consecutive bytes vi-15…vi-1vi. BES Structure BES writes all equations over F256. -

Algebra 1 WORKBOOK Page #1
Algebra 1 WORKBOOK Page #1 Algebra 1 WORKBOOK Page #2 Algebra 1 Unit 1: Relationships Between Quantities Concept 1: Units of Measure Graphically and Situationally Lesson A: Dimensional Analysis (A1.U1.C1.A.____.DimensionalAnalysis) Concept 2: Parts of Expressions and Equations Lesson B: Parts of Expressions (A1.U1.C2.B.___.PartsOfExpressions) Concept 3: Perform Polynomial Operations and Closure Lesson C: Polynomial Expressions (A1.U1.C3.C.____.PolynomialExpressions) Lesson D: Add and Subtract Polynomials (A1.U1.C3.D. ____.AddAndSubtractPolynomials) Lesson E: Multiplying Polynomials (A1.U1.C3.E.____.MultiplyingPolynomials) Concept 4: Radicals and Rational and Irrational Number Properties Lesson F: Simplify Radicals (A1.U1.C4.F.___.≅SimplifyRadicals) Lesson G: Radical Operations (A1.U1.C4.G.___.RadicalOperations) Unit 2: Reasoning with Linear Equations and Inequalities Concept 1: Creating and Solving Linear Equations Lesson A: Equations in 1 Variable (A1.U2.C1.A.____.equations) Lesson B: Inequalities in 1 Variable (A1.U2.C1.B.____.inequalities) Lesson C: Rearranging Formulas (Literal Equations) (A1.U2.C1.C.____.literal) Lesson D: Review of Slope and Graphing Linear (A1.U2.C1.D.____.slopegraph) Equations Lesson E:Writing and Graphing Linear Equations (A1.U2.C1.E.____.writingequations) Lesson F: Systems of Equations (A1.U2.C1.F.____.systemsofeq) Lesson G: Graphing Linear Inequalities and Systems of (A1.U2.C1.G.____.systemsofineq) Linear Inequalities Concept 2: Function Overview with Notation Lesson H: Functions and Function Notation (A1.U2.C2.H.___.functions) -
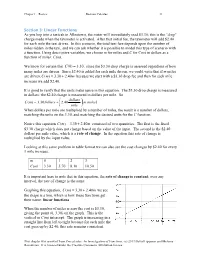
Section 3: Linear Functions
Chapter 1 Review Business Calculus 31 Section 3: Linear Functions As you hop into a taxicab in Allentown, the meter will immediately read $3.30; this is the “drop” charge made when the taximeter is activated. After that initial fee, the taximeter will add $2.40 for each mile the taxi drives. In this scenario, the total taxi fare depends upon the number of miles ridden in the taxi, and we can ask whether it is possible to model this type of scenario with a function. Using descriptive variables, we choose m for miles and C for Cost in dollars as a function of miles: C(m). We know for certain that C(0) = 3.30 , since the $3.30 drop charge is assessed regardless of how many miles are driven. Since $2.40 is added for each mile driven, we could write that if m miles are driven, C(m) = 3.30 + 2.40m because we start with a $3.30 drop fee and then for each mile increase we add $2.40. It is good to verify that the units make sense in this equation. The $3.30 drop charge is measured in dollars; the $2.40 charge is measured in dollars per mile. So dollars C(m) = 3.30dollars + 2.40 (m miles) mile When dollars per mile are multiplied by a number of miles, the result is a number of dollars, matching the units on the 3.30, and matching the desired units for the C function. Notice this equation C(m) = 3.30 + 2.40m consisted of two quantities. -

Chapter 1 Linear Functions
Chapter 1 Linear Functions 11 Sec. 1.1: Slopes and Equations of Lines Date Lines play a very important role in Calculus where we will be approximating complicated functions with lines. We need to be experts with lines to do well in Calculus. In this section, we review slope and equations of lines. Slope of a Line: The slope of a line is defined as the vertical change (the \rise") over the horizontal change (the \run") as one travels along the line. In symbols, taking two different points (x1; y1) and (x2; y2) on the line, the slope is Change in y ∆y y − y m = = = 2 1 : Change in x ∆x x2 − x1 Example: World milk production rose at an approximately constant rate between 1996 and 2003 as shown in the following graph: where M is in million tons and t is the years since 1996. Estimate the slope and interpret it in terms of milk production. 12 Clicker Question 1: Find the slope of the line through the following pair of points (−2; 11) and (3; −4): The slope is (A) Less than -2 (B) Between -2 and 0 (C) Between 0 and 2 (D) More than 2 (E) Undefined It will be helpful to recall the following facts about intercepts. Intercepts: x-intercepts The points where a graph touches the x-axis. If we have an equation, we can find them by setting y = 0. y-intercepts The points where a graph touches the y-axis. If we have an equation, we can find them by setting x = 0. -

Course Syllabus: Math 00023 / Master Templates
Course Name: Math 00023 Course Code: N/A ALEKS Course: Intermediate Algebra Instructor: Master Templates Course Dates: Begin: 08/15/2014 End: 08/15/2015 Course Content: 245 topics Textbook: Miller/O'Neill/Hyde: Intermediate Algebra, 4th Ed. (McGraw-Hill) - ALEKS 360 Chapter R - Review of Basic Algebraic Concepts (26 topics, no due date) Section R.2 (8 topics) Square root of a perfect square Identifying numbers as integers or non-integers Identifying numbers as rational or irrational Translating a sentence by using an inequality symbol Graphing a linear inequality on the number line Translating a sentence into a compound inequality Graphing a compound inequality on the number line Set builder and interval notation Section R.3 (11 topics*) Square root of a perfect square Absolute value of a number Signed fraction multiplication: Advanced Exponents and integers: Problem type 1 Exponents and integers: Problem type 2 Exponents and signed fractions Order of operations with integers and exponents Perimeter of a square or a rectangle Area of a square or a rectangle Circumference and area of a circle Square root of a rational perfect square Section R.4 (4 topics) Properties of addition Using distribution and combining like terms to simplify: Univariate Using distribution with double negation and combining like terms to simplify: Multivariate Combining like terms in a quadratic expression Chapter R Supplementary Topics (4 topics) Signed fraction addition or subtraction: Advanced Signed decimal addition and subtraction with 3 numbers Operations with absolute value: Problem type 2 Properties of real numbers (*) Some topics in this section are also covered in a previous section of this Objective. -

VA-Algebra I - CCL Scope and Sequence
VA-Algebra I - CCL Scope and Sequence Unit Lesson Objectives Integers, Operations, Radicals Expressions in One Variable Identify parts of an expression. Interpret expressions that represent a quantity in terms of its context. Write expressions to represent scenarios. Evaluate one-variable expressions. Equations in One Variable Explain the steps used to solve a two-step, one-variable linear equation. Create two-step, one-variable linear equations to model problems. Solve two-step, one-variable linear equations and simple absolute value equations, pointing out solutions that are viable or not viable in a modeling context. Adding and Subtracting Radicals Identify like radicals. Add and subtract radical expressions. Multiplying Radicals Perform multiplication of radical expressions. Sum and Difference of Two Cubes Recognize a perfect cube and find its cube root. Factor the sum or difference of two cubes. Rewriting Expressions with Radicals Use operations to rewrite expressions involving radicals. Linear Equations and Inequalities Page 1 of 11 VA-Algebra I - CCL Scope and Sequence Unit Lesson Objectives Solving Linear Equations: Variable on One Side Determine the input value that produces the same output value for two functions from a table or graph. Explain the steps used to solve a one-variable linear equation having the variable on one side only. Solve one-variable linear equations having the variable on one side only, pointing out solutions that are viable or not viable in a modeling context. Create one-variable linear equations, having the variable on one side only, to model and solve problems. Solving Linear Equations: Variables on Both Sides Explain the steps used to solve a one-variable linear equation having the variable on both sides.