Sicp.Texi to Correct Errors Or Improve the Art, Then Update the @Set Utfversion 2.Andresraba5.6 Line to Reflect Your Delta
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Administering Unidata on UNIX Platforms
C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta UniData Administering UniData on UNIX Platforms UDT-720-ADMU-1 C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Notices Edition Publication date: July, 2008 Book number: UDT-720-ADMU-1 Product version: UniData 7.2 Copyright © Rocket Software, Inc. 1988-2010. All Rights Reserved. Trademarks The following trademarks appear in this publication: Trademark Trademark Owner Rocket Software™ Rocket Software, Inc. Dynamic Connect® Rocket Software, Inc. RedBack® Rocket Software, Inc. SystemBuilder™ Rocket Software, Inc. UniData® Rocket Software, Inc. UniVerse™ Rocket Software, Inc. U2™ Rocket Software, Inc. U2.NET™ Rocket Software, Inc. U2 Web Development Environment™ Rocket Software, Inc. wIntegrate® Rocket Software, Inc. Microsoft® .NET Microsoft Corporation Microsoft® Office Excel®, Outlook®, Word Microsoft Corporation Windows® Microsoft Corporation Windows® 7 Microsoft Corporation Windows Vista® Microsoft Corporation Java™ and all Java-based trademarks and logos Sun Microsystems, Inc. UNIX® X/Open Company Limited ii SB/XA Getting Started The above trademarks are property of the specified companies in the United States, other countries, or both. All other products or services mentioned in this document may be covered by the trademarks, service marks, or product names as designated by the companies who own or market them. License agreement This software and the associated documentation are proprietary and confidential to Rocket Software, Inc., are furnished under license, and may be used and copied only in accordance with the terms of such license and with the inclusion of the copyright notice. -

COM 113 INTRO to COMPUTER PROGRAMMING Theory Book
1 [Type the document title] UNESCO -NIGERIA TECHNICAL & VOCATIONAL EDUCATION REVITALISATION PROJECT -PHASE II NATIONAL DIPLOMA IN COMPUTER TECHNOLOGY Computer Programming COURSE CODE: COM113 YEAR I - SE MESTER I THEORY Version 1: December 2008 2 [Type the document title] Table of Contents WEEK 1 Concept of programming ................................................................................................................ 6 Features of a good computer program ............................................................................................ 7 System Development Cycle ............................................................................................................ 9 WEEK 2 Concept of Algorithm ................................................................................................................... 11 Features of an Algorithm .............................................................................................................. 11 Methods of Representing Algorithm ............................................................................................ 11 Pseudo code .................................................................................................................................. 12 WEEK 3 English-like form .......................................................................................................................... 15 Flowchart ..................................................................................................................................... -

Design Principles Behind Beauty and Joy of Computing
Paper Session: CS0 SIGCSE ’20, March 11–14, 2020, Portland, OR, USA Design Principles behind Beauty and Joy of Computing Paul Goldenberg June Mark Brian Harvey Al Cuoco Mary Fries EDC EDC UCB EDC EDC Waltham, MA, USA Waltham, MA, USA Berkeley, CA, USA Waltham, MA, USA Waltham, MA, USA [email protected] [email protected] [email protected] [email protected] [email protected] ABSTRACT Technical Symposium on Computer Science Education (SIGCSE’20), March 11–14, 2020, Portland, OR, USA. ACM, NewYork, NY, USA, 7 pages. ACM, This paper shares the design principles of one Advanced Placement New York, NY, USA, 7 pages https://doi.org/10.1145/3328778.3366794 Computer Science Principles (AP CSP) course, Beauty and Joy of Computing (BJC), both for schools considering curriculum, and for 1 Introduction developers in this still-new field. BJC students not only learn about The National Science Foundation (NSF) and College Board (CB) in- CS, but do some and analyze its social implications; we feel that the troduced the Advanced Placement Computer Science Principles (AP job of enticing students into the field isn’t complete until students CSP) course to broaden participation in CS by appealing to high find programming, itself, something they enjoy and know they can school students who didn’t see CS as an inviting option—especially do, and its key ideas accessible. Students must feel invited to use female, black, and Latinx students who have been typically un- their own creativity and logic, and enjoy the power of their logic derrepresented in computing. The AP CSP course was the center- and the beauty and elegance of the code by which they express it. -

Edsger Dijkstra: the Man Who Carried Computer Science on His Shoulders
INFERENCE / Vol. 5, No. 3 Edsger Dijkstra The Man Who Carried Computer Science on His Shoulders Krzysztof Apt s it turned out, the train I had taken from dsger dijkstra was born in Rotterdam in 1930. Nijmegen to Eindhoven arrived late. To make He described his father, at one time the president matters worse, I was then unable to find the right of the Dutch Chemical Society, as “an excellent Aoffice in the university building. When I eventually arrived Echemist,” and his mother as “a brilliant mathematician for my appointment, I was more than half an hour behind who had no job.”1 In 1948, Dijkstra achieved remarkable schedule. The professor completely ignored my profuse results when he completed secondary school at the famous apologies and proceeded to take a full hour for the meet- Erasmiaans Gymnasium in Rotterdam. His school diploma ing. It was the first time I met Edsger Wybe Dijkstra. shows that he earned the highest possible grade in no less At the time of our meeting in 1975, Dijkstra was 45 than six out of thirteen subjects. He then enrolled at the years old. The most prestigious award in computer sci- University of Leiden to study physics. ence, the ACM Turing Award, had been conferred on In September 1951, Dijkstra’s father suggested he attend him three years earlier. Almost twenty years his junior, I a three-week course on programming in Cambridge. It knew very little about the field—I had only learned what turned out to be an idea with far-reaching consequences. a flowchart was a couple of weeks earlier. -

Reinventing Education Based on Data and What Works • Since 1955
Reinventing Education Based on Data and What Works • Since 1955 Carnegie Mellon is reinventing education and the way we think about leveraging technology through its study of the science of learning – an interdisciplinary effort that we’ve been tackling for more than 50 years with both computer scientists and psychologists. CMU's educational technology innovations have inspired numerous startup companies, which are helping students to learn more effectively and efficiently. 1955: Allen Newell (TPR ’57) joins 1995: Prof. Kenneth R. Koedinger (HSS Prof. Herbert Simon’s research team as ’88,’90) and Anderson develop Practical a Ph.D. student. Algebra Tutor. The program pioneers a new form of computer-aided instruction for high 1956: CMU creates one of the world’s first school students based on cognitive tutors. university computation centers. With Prof. Alan Perlis (MCS ’42) as its head, it is a joint 1995: Prof. Jack Mostow (SCS ’81) undertaking of faculty from the business, develops Project LISTEN, an intelligent tutor Simon, Newell psychology, electrical engineering and that helps children learn to read. The National mathematics departments, and the Science Foundation included Project precursor to computer science. LISTEN’s speech recognition system as one of its top 50 innovations from 1950-2000. 1956: Simon creates a “thinking machine”—enacting a mental process 1995: The Center for Automated by breaking it down into its simplest Learning and Discovery is formed, led steps. Later that year, the term “artificial by Prof. Thomas M. Mitchell. intelligence” is coined by a small group Perlis including Newell and Simon. 1998: Spinoff company Carnegie Learning is founded by CMU scientists to expand 1956: Simon, Newell and J. -

Reflexive Interpreters 1 the Problem of Control
Reset reproduction of a Ph.D. thesis proposal submitted June 8, 1978 to the Massachusetts Institute of Technology Electrical Engineering and Computer Science Department. Reset in LaTeX by Jon Doyle, December 1995. c 1978, 1995 Jon Doyle. All rights reserved.. Current address: MIT Laboratory for Computer Science. Available via http://www.medg.lcs.mit.edu/doyle Reflexive Interpreters Jon Doyle [email protected] Massachusetts Institute of Technology, Artificial Intelligence Laboratory Cambridge, Massachusetts 02139, U.S.A. Abstract The goal of achieving powerful problem solving capabilities leads to the “advice taker” form of program and the associated problem of control. This proposal outlines an approach to this problem based on the construction of problem solvers with advanced self-knowledge and introspection capabilities. 1 The Problem of Control Self-reverence, self-knowledge, self-control, These three alone lead life to sovereign power. Alfred, Lord Tennyson, OEnone Know prudent cautious self-control is wisdom’s root. Robert Burns, A Bard’s Epitath The woman that deliberates is lost. Joseph Addison, Cato A major goal of Artificial Intelligence is to construct an “advice taker”,1 a program which can be told new knowledge and advised about how that knowledge may be useful. Many of the approaches towards this goal have proposed constructing additive formalisms for trans- mitting knowledge to the problem solver.2 In spite of considerable work along these lines, formalisms for advising problem solvers about the uses and properties of knowledge are rela- tively undeveloped. As a consequence, the nondeterminism resulting from the uncontrolled application of many independent pieces of knowledge leads to great inefficiencies. -

Getting to Grips with Unix and the Linux Family
Getting to grips with Unix and the Linux family David Chiappini, Giulio Pasqualetti, Tommaso Redaelli Torino, International Conference of Physics Students August 10, 2017 According to the booklet At this end of this session, you can expect: • To have an overview of the history of computer science • To understand the general functioning and similarities of Unix-like systems • To be able to distinguish the features of different Linux distributions • To be able to use basic Linux commands • To know how to build your own operating system • To hack the NSA • To produce the worst software bug EVER According to the booklet update At this end of this session, you can expect: • To have an overview of the history of computer science • To understand the general functioning and similarities of Unix-like systems • To be able to distinguish the features of different Linux distributions • To be able to use basic Linux commands • To know how to build your own operating system • To hack the NSA • To produce the worst software bug EVER A first data analysis with the shell, sed & awk an interactive workshop 1 at the beginning, there was UNIX... 2 ...then there was GNU 3 getting hands dirty common commands wait till you see piping 4 regular expressions 5 sed 6 awk 7 challenge time What's UNIX • Bell Labs was a really cool place to be in the 60s-70s • UNIX was a OS developed by Bell labs • they used C, which was also developed there • UNIX became the de facto standard on how to make an OS UNIX Philosophy • Write programs that do one thing and do it well. -

BERKELEY LOGO 6.1 Berkeley Logo User Manual
BERKELEY LOGO 6.1 Berkeley Logo User Manual Brian Harvey i Short Contents 1 Introduction :::::::::::::::::::::::::::::::::::::::::: 1 2 Data Structure Primitives::::::::::::::::::::::::::::::: 9 3 Communication :::::::::::::::::::::::::::::::::::::: 19 4 Arithmetic :::::::::::::::::::::::::::::::::::::::::: 29 5 Logical Operations ::::::::::::::::::::::::::::::::::: 35 6 Graphics:::::::::::::::::::::::::::::::::::::::::::: 37 7 Workspace Management ::::::::::::::::::::::::::::::: 49 8 Control Structures :::::::::::::::::::::::::::::::::::: 67 9 Macros ::::::::::::::::::::::::::::::::::::::::::::: 83 10 Error Processing ::::::::::::::::::::::::::::::::::::: 87 11 Special Variables ::::::::::::::::::::::::::::::::::::: 89 12 Internationalization ::::::::::::::::::::::::::::::::::: 93 INDEX :::::::::::::::::::::::::::::::::::::::::::::::: 97 iii Table of Contents 1 Introduction ::::::::::::::::::::::::::::::::::::: 1 1.1 Overview ::::::::::::::::::::::::::::::::::::::::::::::::::::::: 1 1.2 Getter/Setter Variable Syntax :::::::::::::::::::::::::::::::::: 2 1.3 Entering and Leaving Logo ::::::::::::::::::::::::::::::::::::: 5 1.4 Tokenization:::::::::::::::::::::::::::::::::::::::::::::::::::: 6 2 Data Structure Primitives :::::::::::::::::::::: 9 2.1 Constructors ::::::::::::::::::::::::::::::::::::::::::::::::::: 9 word ::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 9 list ::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 9 sentence :::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 9 fput :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: -

The Pros of Cons: Programming with Pairs and Lists
The Pros of cons: Programming with Pairs and Lists CS251 Programming Languages Spring 2016, Lyn Turbak Department of Computer Science Wellesley College Racket Values • booleans: #t, #f • numbers: – integers: 42, 0, -273 – raonals: 2/3, -251/17 – floang point (including scien3fic notaon): 98.6, -6.125, 3.141592653589793, 6.023e23 – complex: 3+2i, 17-23i, 4.5-1.4142i Note: some are exact, the rest are inexact. See docs. • strings: "cat", "CS251", "αβγ", "To be\nor not\nto be" • characters: #\a, #\A, #\5, #\space, #\tab, #\newline • anonymous func3ons: (lambda (a b) (+ a (* b c))) What about compound data? 5-2 cons Glues Two Values into a Pair A new kind of value: • pairs (a.k.a. cons cells): (cons v1 v2) e.g., In Racket, - (cons 17 42) type Command-\ to get λ char - (cons 3.14159 #t) - (cons "CS251" (λ (x) (* 2 x)) - (cons (cons 3 4.5) (cons #f #\a)) Can glue any number of values into a cons tree! 5-3 Box-and-pointer diagrams for cons trees (cons v1 v2) v1 v2 Conven3on: put “small” values (numbers, booleans, characters) inside a box, and draw a pointers to “large” values (func3ons, strings, pairs) outside a box. (cons (cons 17 (cons "cat" #\a)) (cons #t (λ (x) (* 2 x)))) 17 #t #\a (λ (x) (* 2 x)) "cat" 5-4 Evaluaon Rules for cons Big step seman3cs: e1 ↓ v1 e2 ↓ v2 (cons) (cons e1 e2) ↓ (cons v1 v2) Small-step seman3cs: (cons e1 e2) ⇒* (cons v1 e2); first evaluate e1 to v1 step-by-step ⇒* (cons v1 v2); then evaluate e2 to v2 step-by-step 5-5 cons evaluaon example (cons (cons (+ 1 2) (< 3 4)) (cons (> 5 6) (* 7 8))) ⇒ (cons (cons 3 (< 3 4)) -

Georgia Department of Revenue
Form MV-9W (Rev. 6-2015) Web and MV Manual Georgia Department of Revenue - Motor Vehicle Division Request for Manufacture of a Special Veteran License Plate ______________________________________________________________________________________ Purpose of this Form: This form is to be used to apply for a military license plate/tag. This form should not be used to record a change of ownership, change of address, or change of license plate classification. Required documentation: You must provide a legible copy of your service discharge (DD-214, DD-215, or for World War II veterans, a WD form) indicating your branch and term of service. If you are an active duty member, a copy of the approved documentation supporting your current membership in the respective reserve or National Guard unit is required. In the case of a retired reserve member from that unit, you must furnish approved documentation supporting the current retired membership status from that reserve unit. OWNER INFORMATION First Name Middle Initial Last Name Suffix Owners’ Full Legal Name: Mailing Address: City: State: Zip: Telephone Number: Owner(s)’ Full Legal Name: First Name Middle Initial Last Name Suffix If secondary Owner(s) are listed Mailing Address: City: State: Zip: Telephone Number: VEHICLE INFORMATION Passenger Vehicle Motorcycle Private Truck Vehicle Identification Number (VIN): Year: Make: Model: CAMPAIGN/TOUR of DUTY Branch of Service: SERVICE AWARD Branch of Service: LICENSE PLATES ______________________ LICENSE PLATES ______________________ World War I World -
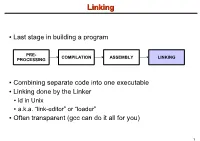
Linking + Libraries
LinkingLinking ● Last stage in building a program PRE- COMPILATION ASSEMBLY LINKING PROCESSING ● Combining separate code into one executable ● Linking done by the Linker ● ld in Unix ● a.k.a. “link-editor” or “loader” ● Often transparent (gcc can do it all for you) 1 LinkingLinking involves...involves... ● Combining several object modules (the .o files corresponding to .c files) into one file ● Resolving external references to variables and functions ● Producing an executable file (if no errors) file1.c file1.o file2.c gcc file2.o Linker Executable fileN.c fileN.o Header files External references 2 LinkingLinking withwith ExternalExternal ReferencesReferences file1.c file2.c int count; #include <stdio.h> void display(void); Compiler extern int count; int main(void) void display(void) { file1.o file2.o { count = 10; with placeholders printf(“%d”,count); display(); } return 0; Linker } ● file1.o has placeholder for display() ● file2.o has placeholder for count ● object modules are relocatable ● addresses are relative offsets from top of file 3 LibrariesLibraries ● Definition: ● a file containing functions that can be referenced externally by a C program ● Purpose: ● easy access to functions used repeatedly ● promote code modularity and re-use ● reduce source and executable file size 4 LibrariesLibraries ● Static (Archive) ● libname.a on Unix; name.lib on DOS/Windows ● Only modules with referenced code linked when compiling ● unlike .o files ● Linker copies function from library into executable file ● Update to library requires recompiling program 5 LibrariesLibraries ● Dynamic (Shared Object or Dynamic Link Library) ● libname.so on Unix; name.dll on DOS/Windows ● Referenced code not copied into executable ● Loaded in memory at run time ● Smaller executable size ● Can update library without recompiling program ● Drawback: slightly slower program startup 6 LibrariesLibraries ● Linking a static library libpepsi.a /* crave source file */ … gcc .. -

The Use of UML for Software Requirements Expression and Management
The Use of UML for Software Requirements Expression and Management Alex Murray Ken Clark Jet Propulsion Laboratory Jet Propulsion Laboratory California Institute of Technology California Institute of Technology Pasadena, CA 91109 Pasadena, CA 91109 818-354-0111 818-393-6258 [email protected] [email protected] Abstract— It is common practice to write English-language 1. INTRODUCTION ”shall” statements to embody detailed software requirements in aerospace software applications. This paper explores the This work is being performed as part of the engineering of use of the UML language as a replacement for the English the flight software for the Laser Ranging Interferometer (LRI) language for this purpose. Among the advantages offered by the of the Gravity Recovery and Climate Experiment (GRACE) Unified Modeling Language (UML) is a high degree of clarity Follow-On (F-O) mission. However, rather than use the real and precision in the expression of domain concepts as well as project’s model to illustrate our approach in this paper, we architecture and design. Can this quality of UML be exploited have developed a separate, ”toy” model for use here, because for the definition of software requirements? this makes it easier to avoid getting bogged down in project details, and instead to focus on the technical approach to While expressing logical behavior, interface characteristics, requirements expression and management that is the subject timeliness constraints, and other constraints on software using UML is commonly done and relatively straight-forward, achiev- of this paper. ing the additional aspects of the expression and management of software requirements that stakeholders expect, especially There is one exception to this choice: we will describe our traceability, is far less so.