DOCSLIB.ORG

11.3 Areas of Polygons

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
11.3 Areas of Polygons 11.3 Areas of Polygons EEssentialssential QQuestionuestion How can you fi nd the area of a regular polygon? CP The center of a regular polygon is the center P apothem of its circumscribed circle. The distance from the center to any side of a regular polygon is called the apothem of a C center regular polygon. Finding the Area of a Regular Polygon Work with a partner. Use dynamic geometry software to construct each regular polygon with side lengths of 4, as shown. Find the apothem and use it to fi nd the area of the polygon. Describe the steps that you used. a. b. 7 4 D 6 C 5 3 E 4 C 2 3 2 1 1 A 0 B A 0 B −3 −2 −1 031 2 −5 −4 −3 −2 −1 03451 2 c. 8 d. F 10 E E D 9 7 8 6 G 7 D 5 6 4 5 F C 4 3 H 3 C 2 2 1 1 A 0 B A 0 B −5 −4 −3 −2 −1 03451 2 −6 −5 −4 −3 −2 −1 01 2 3456 Writing a Formula for Area Work with a partner. Generalize the steps you used in Exploration 1 to develop a REASONING formula for the area of a regular polygon. ABSTRACTLY To be profi cient in math, CCommunicateommunicate YourYour AnswerAnswer you need to know and fl exibly use different 3. How can you fi nd the area of a regular polygon? properties of operations 4. Regular pentagon ABCDE has side lengths of 6 meters and an apothem of and objects. approximately 4.13 meters. Find the area of ABCDE. Section 11.3 Areas of Polygons 609 hhs_geo_pe_1103.indds_geo_pe_1103.indd 609609 11/19/15/19/15 33:16:16 PMPM 11.3 Lesson WWhathat YYouou WWillill LLearnearn Find areas of rhombuses and kites. Find angle measures in regular polygons. Core VocabularyVocabulary Find areas of regular polygons. center of a regular polygon, p. 611 Finding Areas of Rhombuses and Kites radius of a regular polygon, d d p. 611 You can divide a rhombus or kite with diagonals 1 and 2 into two congruent triangles 1 1 1 1 apothem of a regular polygon, with base d , height — d , and area — d — d = — d d . So, the area of a rhombus or kite 1 2 2 2 1( 2 2) 4 1 2 p. 611 —1 d d = —1 d d is 2( 1 2 ) 1 2. central angle of a regular 4 2 polygon, p. 611 A = 1 d d A = 1 d d 4 1 2 4 1 2 Previous 1 d 1 d d 2 2 d 2 2 rhombus 2 2 kite d d 1 1 CCoreore CConceptoncept Area of a Rhombus or Kite 1 d d — d d The area of a rhombus or kite with diagonals 1 and 2 is 2 1 2. d d 2 2 d d 1 1 Finding the Area of a Rhombus or Kite Find the area of each rhombus or kite. a. b. 8 m 7 cm 6 m 10 cm SOLUTION 1 1 A = — d d A = — d d a. 2 1 2 b. 2 1 2 1 1 = — = — 2 (6)(8) 2 (10)(7) = 24 = 35 So, the area is 24 square meters. So, the area is 35 square centimeters. MMonitoringonitoring PProgressrogress Help in English and Spanish at BigIdeasMath.com d = d = 1. Find the area of a rhombus with diagonals 1 4 feet and 2 5 feet. d = d = 2. Find the area of a kite with diagonals 1 12 inches and 2 9 inches. 610 Chapter 11 Circumference, Area, and Volume hhs_geo_pe_1103.indds_geo_pe_1103.indd 610610 11/19/15/19/15 33:16:16 PMPM Finding Angle Measures in Regular Polygons The diagram shows a regular polygon inscribed in a circle. M The center of a regular polygon and the radius of a apothem regular polygon are the center and the radius of its Q PQ center circumscribed circle. P N The distance from the center to any side of a regular radius PN polygon is called the apothem of a regular polygon. The apothem is the height to the base of an isosceles ∠MPN triangle that has two radii as legs. The word “apothem” is a central angle. refers to a segment as well as a length. For a given regular polygon, think of an apothem as a segment and the apothem as a length. A central angle of a regular polygon is an angle formed by two radii drawn to consecutive vertices of the polygon. To fi nd the measure of each central angle, divide 360° by the number of sides. Finding Angle Measures in a Regular Polygon In the diagram, ABCDE is a regular pentagon inscribed in ⊙F. Find each angle measure. C B D F G A E m∠AFB m∠AFG m∠GAF ANALYZING a. b. c. RELATIONSHIPS SOLUTION FG — is an altitude of an 360° a. ∠AFB is a central angle, so m∠AFB = — = 72°. isosceles triangle, so 5 it is also a median and — angle bisector of the b. FG is an apothem, which makes it an altitude of isosceles △AFB. isosceles triangle. — 1 So, FG bisects ∠AFB and m∠AFG = — m∠AFB = 36°. 2 c. By the Triangle Sum Theorem (Theorem 5.1), the sum of the angle measures of right △GAF is 180°. m∠GAF = 180° − 90° − 36° = 54° So, m∠GAF = 54°. MMonitoringonitoring PProgressrogress Help in English and Spanish at BigIdeasMath.com In the diagram, WXYZ is a square inscribed in ⊙P. X Y Q 3. Identify the center, a radius, an apothem, and a central angle of the polygon. P 4. Find m∠XPY, m∠XPQ, and m∠PXQ. W Z Section 11.3 Areas of Polygons 611 hhs_geo_pe_1103.indds_geo_pe_1103.indd 611611 11/19/15/19/15 33:16:16 PMPM Finding Areas of Regular Polygons You can fi nd the area of any regular n-gon by dividing it into congruent triangles. A = Area of one triangle ⋅ Number of triangles READING 1 Base of triangle is s and height of = — ⋅ s ⋅ a ⋅ n DIAGRAMS ( 2 ) triangle is a. Number of triangles is n. In this book, a point 1 Commutative and Associative = — a n s 2 ⋅ ⋅ ( ⋅ ) shown inside a regular Properties of Multiplication a s polygon marks the center 1 There are n congruent sides of of the circle that can be = — a ⋅ P 2 length s, so perimeter P is n ⋅ s. circumscribed about the polygon. CCoreore CConceptoncept Area of a Regular Polygon The area of a regular n-gon with side length s is one-half the product of the apothem a and the perimeter P. 1 1 a A = — aP A = — a ns s 2 , or 2 ⋅ Finding the Area of a Regular Polygon A regular nonagon is inscribed in a circle with a radius of 4 units. Find the area of the nonagon. K 4 L M 4 J SOLUTION 360° — ∠JLK — ° LM The measure of central is 9 , or 40 . Apothem bisects the central angle, so m∠KLM is 20°. To fi nd the lengths of the legs, use trigonometric ratios for right △KLM. L 20° 4 4 J M K MK LM ° = — ° = — sin 20 LK cos 20 LK MK LM sin 20° = — cos 20° = — 4 4 4 sin 20° = MK 4 cos 20° = LM The regular nonagon has side length s = 2(MK) = 2(4 sin 20°) = 8 sin 20°, and apothem a = LM = 4 cos 20°. 1 1 A = — a ns = — ° ° ≈ So, the area is 2 ⋅ 2 (4 cos 20 ) ⋅ (9)(8 sin 20 ) 46.3 square units. 612 Chapter 11 Circumference, Area, and Volume hhs_geo_pe_1103.indds_geo_pe_1103.indd 612612 11/19/15/19/15 33:16:16 PMPM Finding the Area of a Regular Polygon You are decorating the top of a table by covering it with small ceramic tiles. The tabletop is a regular octagon with 15-inch sides and a radius of about 19.6 inches. What is the area you are covering? R 15 in. 19.6 in. PQ SOLUTION Step 1 Find the perimeter P of the tabletop. An octagon has 8 sides, so P = 8(15) = 120 inches. Step 2 Find the apothem a. The apothem is height RS of △PQR. — — Because △PQR is isosceles, altitude RS bisects QP . 1 1 QS = — QP = — = So, 2 ( ) 2 (15) 7.5 inches. R 19.6 in. P S Q 7.5 in. To fi nd RS, use the Pythagorean Theorem (Theorem 9.1) for △RQS. —— — a = RS = √19.62 − 7.52 = √327.91 ≈ 18.108 Step 3 Find the area A of the tabletop. 1 A = — aP 2 Formula for area of a regular polygon — 1 = — √ 2 ( 327.91 ) (120) Substitute. ≈ 1086.5 Simplify. The area you are covering with tiles is about 1086.5 square inches. MMonitoringonitoring PProgressrogress Help in English and Spanish at BigIdeasMath.com Find the area of the regular polygon. 5. 6. 7 8 6.5 Section 11.3 Areas of Polygons 613 hhs_geo_pe_1103.indds_geo_pe_1103.indd 613613 11/19/15/19/15 33:16:16 PMPM 11.3 Exercises Dynamic Solutions available at BigIdeasMath.com VVocabularyocabulary andand CoreCore ConceptConcept CheckCheck 1. WRITING Explain how to fi nd the measure of a central angle of a regular polygon. 2. DIFFERENT WORDS, SAME QUESTION Which is different? Find “both” answers. B A 8 Find the radius of ⊙F. Find the apothem of polygon ABCDE. 5.5 G C F 6.8 Find AF. Find the radius of polygon ABCDE. E D MMonitoringonitoring ProgressProgress andand ModelingModeling withwith MathematicsMathematics In Exercises 3–6, fi nd the area of the kite or rhombus.
Load more

Recommended publications
  • And Twelve-Pointed Star Polygon Design of the Tashkent Scrolls
    Bridges 2011: Mathematics, Music, Art, Architecture, Culture A Nine- and Twelve-Pointed Star Polygon Design of the Tashkent Scrolls B. Lynn Bodner Mathematics Department Cedar Avenue Monmouth University West Long Branch, New Jersey, 07764, USA E-mail: [email protected] Abstract In this paper we will explore one of the Tashkent Scrolls’ repeat units, that, when replicated using symmetry operations, creates an overall pattern consisting of “nearly regular” nine-pointed, regular twelve-pointed and irregularly-shaped pentagonal star polygons. We seek to determine how the original designer of this pattern may have determined, without mensuration, the proportion and placement of the star polygons comprising the design. We will do this by proposing a plausible Euclidean “point-joining” compass-and-straightedge reconstruction. Introduction The Tashkent Scrolls (so named because they are housed in Tashkent at the Institute of Oriental Studies at the Academy of Sciences) consist of fragments of architectural sketches attributed to an Uzbek master builder or a guild of architects practicing in 16 th century Bukhara [1, p. 7]. The sketch from the Tashkent Scrolls that we will explore shows only a small portion, or the repeat unit , of a nine- and twelve-pointed star polygon design. It is contained within a rectangle and must be reflected across the boundaries of this rectangle to achieve the entire pattern. This drawing, which for the remainder of this paper we will refer to as “T9N12,” is similar to many of the 114 Islamic architectural and ornamental design sketches found in the much larger, older and better preserved Topkapı Scroll, a 96-foot-long architectural scroll housed at the Topkapı Palace Museum Library in Istanbul.
    [Show full text]
  • Islamic Geometric Ornaments in Istanbul
    ►SKETCH 2 CONSTRUCTIONS OF REGULAR POLYGONS Regular polygons are the base elements for constructing the majority of Islamic geometric ornaments. Of course, in Islamic art there are geometric ornaments that may have different genesis, but those that can be created from regular polygons are the most frequently seen in Istanbul. We can also notice that many of the Islamic geometric ornaments can be recreated using rectangular grids like the ornament in our first example. Sometimes methods using rectangular grids are much simpler than those based or regular polygons. Therefore, we should not omit these methods. However, because methods for constructing geometric ornaments based on regular polygons are the most popular, we will spend relatively more time explor- ing them. Before, we start developing some concrete constructions it would be worthwhile to look into a few issues of a general nature. As we have no- ticed while developing construction of the ornament from the floor in the Sultan Ahmed Mosque, these constructions are not always simple, and in order to create them we need some knowledge of elementary geometry. On the other hand, computer programs for geometry or for computer graphics can give us a number of simpler ways to develop geometric fig- ures. Some of them may not require any knowledge of geometry. For ex- ample, we can create a regular polygon with any number of sides by rotat- ing a point around another point by using rotations 360/n degrees. This is a very simple task if we use a computer program and the only knowledge of geometry we need here is that the full angle is 360 degrees.
    [Show full text]
  • Build a Tetrahedral Kite
    Aeronautics Research Mission Directorate Build a Tetrahedral Kite Suggested Grades: 8-12 Activity Overview Time: 90-120 minutes In this activity, you will build a tetrahedral kite from Materials household supplies. • 24 straws (8 inches or less) - NOTE: The straws need to be Steps straight and the same length. If only flexible straws are available, 1. Cut a length of yarn/string 4 feet long. then cut off the flexible portion. • Two or three large spools of 2. Take six straws and place them on a flat surface. cotton string or yarn (approximately 100 feet total) 3. Use your piece of string to join three straws • Scissors together in a triangular shape. On the side where • Hot glue gun and hot glue sticks the two strings are extending from it, one end • Ruler or dowel rod for kite bridle should be approximately 20 inches long, and the • Four pieces of tissue paper (24 x other should be approximately 4 inches long. 18 inches or larger) See Figure 1. • All-purpose glue stick Figure 1 4. Tie these two ends of the string tightly together. Make sure there is no room for the triangle to wiggle. 5. The three straws should form a tight triangle. 6. Cut another 4-inch piece of string. 7. Take one end of the 4-inch string, and tie that end to a corner of the triangle that does not have the string ends extending from it. Figure 2. 8. Add two more straws onto the longest piece of string. 9. Next, take the string that holds the two additional straws and tie it to the end of one of the 4-inch strings to make another tight triangle.
    [Show full text]
  • Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
    SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface.
    [Show full text]
  • Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1
    Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1. Acute angle: Angle whose measure is greater than 0° and less than 90°. 2. Adjacent angles: Two angles that have a common side and a common vertex. 3. Alternate interior angles: A pair of angles in the interior of a figure formed by two lines and a transversal, lying on alternate sides of the transversal and having different vertices. 4. Altitude: Perpendicular segment from a vertex of a triangle to the opposite side or the line containing the opposite side. 5. Angle: A figure formed by two rays with a common endpoint. 6. Angle bisector: Ray that divides an angle into two congruent angles and bisects the angle. 7. Base Angles: Two angles not included in the legs of an isosceles triangle. 8. Bisect: To divide a segment or an angle into two congruent parts. 9. Coincide: To lie on top of the other. A line can coincide another line. 10. Collinear: Lying on the same line. 11. Complimentary: Two angle’s whose sum is 90°. 12. Concave Polygon: Polygon in which at least one interior angle measures more than 180° (at least one segment connecting two vertices is outside the polygon). 13. Conclusion: A result of summary of all the work that has been completed. The part of a conditional statement that occurs after the word “then”. 14. Congruent parts: Two or more parts that only have the same measure. In CPCTC, the parts of the congruent triangles are congruent. 15. Congruent triangles: Two triangles are congruent if and only if all of their corresponding parts are congruent.
    [Show full text]
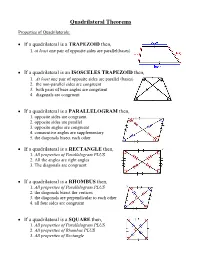
  • Quadrilateral Theorems
    Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3.
    [Show full text]
  • Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur Si Muove: Biomimetic Embedding of N-Tuple Helices in Spherical Polyhedra - /
    Alternative view of segmented documents via Kairos 23 October 2017 | Draft Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur si muove: Biomimetic embedding of N-tuple helices in spherical polyhedra - / - Introduction Symbolic stars vs Strategic pillars; Polyhedra vs Helices; Logic vs Comprehension? Dynamic bonding patterns in n-tuple helices engendering n-fold rotating symbols Embedding the triple helix in a spherical octahedron Embedding the quadruple helix in a spherical cube Embedding the quintuple helix in a spherical dodecahedron and a Pentagramma Mirificum Embedding six-fold, eight-fold and ten-fold helices in appropriately encircled polyhedra Embedding twelve-fold, eleven-fold, nine-fold and seven-fold helices in appropriately encircled polyhedra Neglected recognition of logical patterns -- especially of opposition Dynamic relationship between polyhedra engendered by circles -- variously implying forms of unity Symbol rotation as dynamic essential to engaging with value-inversion References Introduction The contrast to the geocentric model of the solar system was framed by the Italian mathematician, physicist and philosopher Galileo Galilei (1564-1642). His much-cited phrase, " And yet it moves" (E pur si muove or Eppur si muove) was allegedly pronounced in 1633 when he was forced to recant his claims that the Earth moves around the immovable Sun rather than the converse -- known as the Galileo affair. Such a shift in perspective might usefully inspire the recognition that the stasis attributed so widely to logos and other much-valued cultural and heraldic symbols obscures the manner in which they imply a fundamental cognitive dynamic. Cultural symbols fundamental to the identity of a group might then be understood as variously moving and transforming in ways which currently elude comprehension.
    [Show full text]
  • Applying the Polygon Angle
    POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°.
    [Show full text]
  • Polygon Review and Puzzlers in the Above, Those Are Names to the Polygons: Fill in the Blank Parts. Names: Number of Sides
    Polygon review and puzzlers ÆReview to the classification of polygons: Is it a Polygon? Polygons are 2-dimensional shapes. They are made of straight lines, and the shape is "closed" (all the lines connect up). Polygon Not a Polygon Not a Polygon (straight sides) (has a curve) (open, not closed) Regular polygons have equal length sides and equal interior angles. Polygons are named according to their number of sides. Name of Degree of Degree of triangle total angles regular angles Triangle 180 60 In the above, those are names to the polygons: Quadrilateral 360 90 fill in the blank parts. Pentagon Hexagon Heptagon 900 129 Names: number of sides: Octagon Nonagon hendecagon, 11 dodecagon, _____________ Decagon 1440 144 tetradecagon, 13 hexadecagon, 15 Do you see a pattern in the calculation of the heptadecagon, _____________ total degree of angles of the polygon? octadecagon, _____________ --- (n -2) x 180° enneadecagon, _____________ icosagon 20 pentadecagon, _____________ These summation of angles rules, also apply to the irregular polygons, try it out yourself !!! A point where two or more straight lines meet. Corner. Example: a corner of a polygon (2D) or of a polyhedron (3D) as shown. The plural of vertex is "vertices” Test them out yourself, by drawing diagonals on the polygons. Here are some fun polygon riddles; could you come up with the answer? Geometry polygon riddles I: My first is in shape and also in space; My second is in line and also in place; My third is in point and also in line; My fourth in operation but not in sign; My fifth is in angle but not in degree; My sixth is in glide but not symmetry; Geometry polygon riddles II: I am a polygon all my angles have the same measure all my five sides have the same measure, what general shape am I? Geometry polygon riddles III: I am a polygon.
    [Show full text]
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • Interior and Exterior Angles of Polygons 2A
    Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org G.CO.C.11: Interior and Exterior Angles of Polygons 2a 1 Which type of figure is shown in the accompanying 5 In the diagram below of regular pentagon ABCDE, diagram? EB is drawn. 1) hexagon 2) octagon 3) pentagon 4) quadrilateral What is the measure of ∠AEB? 2 What is the measure of each interior angle of a 1) 36º regular hexagon? 2) 54º 1) 60° 3) 72º 2) 120° 4) 108º 3) 135° 4) 270° 6 What is the measure, in degrees, of each exterior angle of a regular hexagon? 3 Determine, in degrees, the measure of each interior 1) 45 angle of a regular octagon. 2) 60 3) 120 4) 135 4 Determine and state the measure, in degrees, of an interior angle of a regular decagon. 7 A stop sign in the shape of a regular octagon is resting on a brick wall, as shown in the accompanying diagram. What is the measure of angle x? 1) 45° 2) 60° 3) 120° 4) 135° 1 Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org 8 One piece of the birdhouse that Natalie is building 12 The measure of an interior angle of a regular is shaped like a regular pentagon, as shown in the polygon is 120°. How many sides does the polygon accompanying diagram. have? 1) 5 2) 6 3) 3 4) 4 13 Melissa is walking around the outside of a building that is in the shape of a regular polygon.
    [Show full text]
  • Pentagonal Pyramid
    Chapter 9 Surfaces and Solids Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and 9.2 Volume Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and Volume The solids (space figures) shown in Figure 9.14 below are pyramids. In Figure 9.14(a), point A is noncoplanar with square base BCDE. In Figure 9.14(b), F is noncoplanar with its base, GHJ. (a) (b) Figure 9.14 3 Pyramids, Area, and Volume In each space pyramid, the noncoplanar point is joined to each vertex as well as each point of the base. A solid pyramid results when the noncoplanar point is joined both to points on the polygon as well as to points in its interior. Point A is known as the vertex or apex of the square pyramid; likewise, point F is the vertex or apex of the triangular pyramid. The pyramid of Figure 9.14(b) has four triangular faces; for this reason, it is called a tetrahedron. 4 Pyramids, Area, and Volume The pyramid in Figure 9.15 is a pentagonal pyramid. It has vertex K, pentagon LMNPQ for its base, and lateral edges and Although K is called the vertex of the pyramid, there are actually six vertices: K, L, M, N, P, and Q. Figure 9.15 The sides of the base and are base edges. 5 Pyramids, Area, and Volume All lateral faces of a pyramid are triangles; KLM is one of the five lateral faces of the pentagonal pyramid. Including base LMNPQ, this pyramid has a total of six faces. The altitude of the pyramid, of length h, is the line segment from the vertex K perpendicular to the plane of the base.
    [Show full text]