On the Estimation of Prediction Errors in Linear Regression Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 12 Robust Estimation
Lecture 12 Robust Estimation Prof. Dr. Svetlozar Rachev Institute for Statistics and Mathematical Economics University of Karlsruhe Financial Econometrics, Summer Semester 2007 Prof. Dr. Svetlozar Rachev Institute for Statistics and MathematicalLecture Economics 12 Robust University Estimation of Karlsruhe Copyright These lecture-notes cannot be copied and/or distributed without permission. The material is based on the text-book: Financial Econometrics: From Basics to Advanced Modeling Techniques (Wiley-Finance, Frank J. Fabozzi Series) by Svetlozar T. Rachev, Stefan Mittnik, Frank Fabozzi, Sergio M. Focardi,Teo Jaˇsic`. Prof. Dr. Svetlozar Rachev Institute for Statistics and MathematicalLecture Economics 12 Robust University Estimation of Karlsruhe Outline I Robust statistics. I Robust estimators of regressions. I Illustration: robustness of the corporate bond yield spread model. Prof. Dr. Svetlozar Rachev Institute for Statistics and MathematicalLecture Economics 12 Robust University Estimation of Karlsruhe Robust Statistics I Robust statistics addresses the problem of making estimates that are insensitive to small changes in the basic assumptions of the statistical models employed. I The concepts and methods of robust statistics originated in the 1950s. However, the concepts of robust statistics had been used much earlier. I Robust statistics: 1. assesses the changes in estimates due to small changes in the basic assumptions; 2. creates new estimates that are insensitive to small changes in some of the assumptions. I Robust statistics is also useful to separate the contribution of the tails from the contribution of the body of the data. Prof. Dr. Svetlozar Rachev Institute for Statistics and MathematicalLecture Economics 12 Robust University Estimation of Karlsruhe Robust Statistics I Peter Huber observed, that robust, distribution-free, and nonparametrical actually are not closely related properties. -

Should We Think of a Different Median Estimator?
Comunicaciones en Estad´ıstica Junio 2014, Vol. 7, No. 1, pp. 11–17 Should we think of a different median estimator? ¿Debemos pensar en un estimator diferente para la mediana? Jorge Iv´an V´eleza Juan Carlos Correab [email protected] [email protected] Resumen La mediana, una de las medidas de tendencia central m´as populares y utilizadas en la pr´actica, es el valor num´erico que separa los datos en dos partes iguales. A pesar de su popularidad y aplicaciones, muchos desconocen la existencia de dife- rentes expresiones para calcular este par´ametro. A continuaci´on se presentan los resultados de un estudio de simulaci´on en el que se comparan el estimador cl´asi- co y el propuesto por Harrell & Davis (1982). Mostramos que, comparado con el estimador de Harrell–Davis, el estimador cl´asico no tiene un buen desempe˜no pa- ra tama˜nos de muestra peque˜nos. Basados en los resultados obtenidos, se sugiere promover la utilizaci´on de un mejor estimador para la mediana. Palabras clave: mediana, cuantiles, estimador Harrell-Davis, simulaci´on estad´ısti- ca. Abstract The median, one of the most popular measures of central tendency widely-used in the statistical practice, is often described as the numerical value separating the higher half of the sample from the lower half. Despite its popularity and applica- tions, many people are not aware of the existence of several formulas to estimate this parameter. We present the results of a simulation study comparing the classic and the Harrell-Davis (Harrell & Davis 1982) estimators of the median for eight continuous statistical distributions. -

04 – Everything You Want to Know About Correlation but Were
EVERYTHING YOU WANT TO KNOW ABOUT CORRELATION BUT WERE AFRAID TO ASK F R E D K U O 1 MOTIVATION • Correlation as a source of confusion • Some of the confusion may arise from the literary use of the word to convey dependence as most people use “correlation” and “dependence” interchangeably • The word “correlation” is ubiquitous in cost/schedule risk analysis and yet there are a lot of misconception about it. • A better understanding of the meaning and derivation of correlation coefficient, and what it truly measures is beneficial for cost/schedule analysts. • Many times “true” correlation is not obtainable, as will be demonstrated in this presentation, what should the risk analyst do? • Is there any other measures of dependence other than correlation? • Concordance and Discordance • Co-monotonicity and Counter-monotonicity • Conditional Correlation etc. 2 CONTENTS • What is Correlation? • Correlation and dependence • Some examples • Defining and Estimating Correlation • How many data points for an accurate calculation? • The use and misuse of correlation • Some example • Correlation and Cost Estimate • How does correlation affect cost estimates? • Portfolio effect? • Correlation and Schedule Risk • How correlation affect schedule risks? • How Shall We Go From Here? • Some ideas for risk analysis 3 POPULARITY AND SHORTCOMINGS OF CORRELATION • Why Correlation Is Popular? • Correlation is a natural measure of dependence for a Multivariate Normal Distribution (MVN) and the so-called elliptical family of distributions • It is easy to calculate analytically; we only need to calculate covariance and variance to get correlation • Correlation and covariance are easy to manipulate under linear operations • Correlation Shortcomings • Variances of R.V. -

11. Correlation and Linear Regression
11. Correlation and linear regression The goal in this chapter is to introduce correlation and linear regression. These are the standard tools that statisticians rely on when analysing the relationship between continuous predictors and continuous outcomes. 11.1 Correlations In this section we’ll talk about how to describe the relationships between variables in the data. To do that, we want to talk mostly about the correlation between variables. But first, we need some data. 11.1.1 The data Table 11.1: Descriptive statistics for the parenthood data. variable min max mean median std. dev IQR Dan’s grumpiness 41 91 63.71 62 10.05 14 Dan’s hours slept 4.84 9.00 6.97 7.03 1.02 1.45 Dan’s son’s hours slept 3.25 12.07 8.05 7.95 2.07 3.21 ............................................................................................ Let’s turn to a topic close to every parent’s heart: sleep. The data set we’ll use is fictitious, but based on real events. Suppose I’m curious to find out how much my infant son’s sleeping habits affect my mood. Let’s say that I can rate my grumpiness very precisely, on a scale from 0 (not at all grumpy) to 100 (grumpy as a very, very grumpy old man or woman). And lets also assume that I’ve been measuring my grumpiness, my sleeping patterns and my son’s sleeping patterns for - 251 - quite some time now. Let’s say, for 100 days. And, being a nerd, I’ve saved the data as a file called parenthood.csv. -

Bias, Mean-Square Error, Relative Efficiency
3 Evaluating the Goodness of an Estimator: Bias, Mean-Square Error, Relative Efficiency Consider a population parameter ✓ for which estimation is desired. For ex- ample, ✓ could be the population mean (traditionally called µ) or the popu- lation variance (traditionally called σ2). Or it might be some other parame- ter of interest such as the population median, population mode, population standard deviation, population minimum, population maximum, population range, population kurtosis, or population skewness. As previously mentioned, we will regard parameters as numerical charac- teristics of the population of interest; as such, a parameter will be a fixed number, albeit unknown. In Stat 252, we will assume that our population has a distribution whose density function depends on the parameter of interest. Most of the examples that we will consider in Stat 252 will involve continuous distributions. Definition 3.1. An estimator ✓ˆ is a statistic (that is, it is a random variable) which after the experiment has been conducted and the data collected will be used to estimate ✓. Since it is true that any statistic can be an estimator, you might ask why we introduce yet another word into our statistical vocabulary. Well, the answer is quite simple, really. When we use the word estimator to describe a particular statistic, we already have a statistical estimation problem in mind. For example, if ✓ is the population mean, then a natural estimator of ✓ is the sample mean. If ✓ is the population variance, then a natural estimator of ✓ is the sample variance. More specifically, suppose that Y1,...,Yn are a random sample from a population whose distribution depends on the parameter ✓.The following estimators occur frequently enough in practice that they have special notations. -

Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10
International Journal of Environmental Research and Public Health Article Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10 Rudy de Barros Ahrens 1,*, Luciana da Silva Lirani 2 and Antonio Carlos de Francisco 3 1 Department of Business, Faculty Sagrada Família (FASF), Ponta Grossa, PR 84010-760, Brazil 2 Department of Health Sciences Center, State University Northern of Paraná (UENP), Jacarezinho, PR 86400-000, Brazil; [email protected] 3 Department of Industrial Engineering and Post-Graduation in Production Engineering, Federal University of Technology—Paraná (UTFPR), Ponta Grossa, PR 84017-220, Brazil; [email protected] * Correspondence: [email protected] Received: 1 September 2020; Accepted: 29 September 2020; Published: 9 October 2020 Abstract: The purpose of this study was to validate the construct and reliability of an instrument to assess the work environment as a single tool based on quality of life (QL), quality of work life (QWL), and organizational climate (OC). The methodology tested the construct validity through Exploratory Factor Analysis (EFA) and reliability through Cronbach’s alpha. The EFA returned a Kaiser–Meyer–Olkin (KMO) value of 0.917; which demonstrated that the data were adequate for the factor analysis; and a significant Bartlett’s test of sphericity (χ2 = 7465.349; Df = 1225; p 0.000). ≤ After the EFA; the varimax rotation method was employed for a factor through commonality analysis; reducing the 14 initial factors to 10. Only question 30 presented commonality lower than 0.5; and the other questions returned values higher than 0.5 in the commonality analysis. Regarding the reliability of the instrument; all of the questions presented reliability as the values varied between 0.953 and 0.956. -
14: Correlation
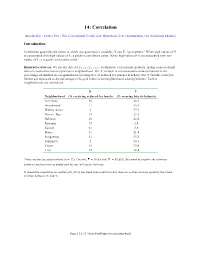
14: Correlation Introduction | Scatter Plot | The Correlational Coefficient | Hypothesis Test | Assumptions | An Additional Example Introduction Correlation quantifies the extent to which two quantitative variables, X and Y, “go together.” When high values of X are associated with high values of Y, a positive correlation exists. When high values of X are associated with low values of Y, a negative correlation exists. Illustrative data set. We use the data set bicycle.sav to illustrate correlational methods. In this cross-sectional data set, each observation represents a neighborhood. The X variable is socioeconomic status measured as the percentage of children in a neighborhood receiving free or reduced-fee lunches at school. The Y variable is bicycle helmet use measured as the percentage of bicycle riders in the neighborhood wearing helmets. Twelve neighborhoods are considered: X Y Neighborhood (% receiving reduced-fee lunch) (% wearing bicycle helmets) Fair Oaks 50 22.1 Strandwood 11 35.9 Walnut Acres 2 57.9 Discov. Bay 19 22.2 Belshaw 26 42.4 Kennedy 73 5.8 Cassell 81 3.6 Miner 51 21.4 Sedgewick 11 55.2 Sakamoto 2 33.3 Toyon 19 32.4 Lietz 25 38.4 Three are twelve observations (n = 12). Overall, = 30.83 and = 30.883. We want to explore the relation between socioeconomic status and the use of bicycle helmets. It should be noted that an outlier (84, 46.6) has been removed from this data set so that we may quantify the linear relation between X and Y. Page 14.1 (C:\data\StatPrimer\correlation.wpd) Scatter Plot The first step is create a scatter plot of the data. -

A Joint Central Limit Theorem for the Sample Mean and Regenerative Variance Estimator*
Annals of Operations Research 8(1987)41-55 41 A JOINT CENTRAL LIMIT THEOREM FOR THE SAMPLE MEAN AND REGENERATIVE VARIANCE ESTIMATOR* P.W. GLYNN Department of Industrial Engineering, University of Wisconsin, Madison, W1 53706, USA and D.L. IGLEHART Department of Operations Research, Stanford University, Stanford, CA 94305, USA Abstract Let { V(k) : k t> 1 } be a sequence of independent, identically distributed random vectors in R d with mean vector ~. The mapping g is a twice differentiable mapping from R d to R 1. Set r = g(~). A bivariate central limit theorem is proved involving a point estimator for r and the asymptotic variance of this point estimate. This result can be applied immediately to the ratio estimation problem that arises in regenerative simulation. Numerical examples show that the variance of the regenerative variance estimator is not necessarily minimized by using the "return state" with the smallest expected cycle length. Keywords and phrases Bivariate central limit theorem,j oint limit distribution, ratio estimation, regenerative simulation, simulation output analysis. 1. Introduction Let X = {X(t) : t I> 0 } be a (possibly) delayed regenerative process with regeneration times 0 = T(- 1) ~< T(0) < T(1) < T(2) < .... To incorporate regenerative sequences {Xn: n I> 0 }, we pass to the continuous time process X = {X(t) : t/> 0}, where X(0 = X[t ] and [t] is the greatest integer less than or equal to t. Under quite general conditions (see Smith [7] ), *This research was supported by Army Research Office Contract DAAG29-84-K-0030. The first author was also supported by National Science Foundation Grant ECS-8404809 and the second author by National Science Foundation Grant MCS-8203483. -

CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (Moderately Hard)Or
5 COMPUTING CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (moderately hard)or WHAT YOU WILLpost, LEARN IN THIS CHAPTER • Understanding what correlations are and how they work • Computing a simple correlation coefficient • Interpretingcopy, the value of the correlation coefficient • Understanding what other types of correlations exist and when they notshould be used Do WHAT ARE CORRELATIONS ALL ABOUT? Measures of central tendency and measures of variability are not the only descrip- tive statistics that we are interested in using to get a picture of what a set of scores 76 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 5 ■ Computing Correlation Coefficients 77 looks like. You have already learned that knowing the values of the one most repre- sentative score (central tendency) and a measure of spread or dispersion (variability) is critical for describing the characteristics of a distribution. However, sometimes we are as interested in the relationship between variables—or, to be more precise, how the value of one variable changes when the value of another variable changes. The way we express this interest is through the computation of a simple correlation coefficient. For example, what’s the relationship between age and strength? Income and years of education? Memory skills and amount of drug use? Your political attitudes and the attitudes of your parents? A correlation coefficient is a numerical index that reflects the relationship or asso- ciation between two variables. The value of this descriptive statistic ranges between −1.00 and +1.00. -

1 Estimation and Beyond in the Bayes Universe
ISyE8843A, Brani Vidakovic Handout 7 1 Estimation and Beyond in the Bayes Universe. 1.1 Estimation No Bayes estimate can be unbiased but Bayesians are not upset! No Bayes estimate with respect to the squared error loss can be unbiased, except in a trivial case when its Bayes’ risk is 0. Suppose that for a proper prior ¼ the Bayes estimator ±¼(X) is unbiased, Xjθ (8θ)E ±¼(X) = θ: This implies that the Bayes risk is 0. The Bayes risk of ±¼(X) can be calculated as repeated expectation in two ways, θ Xjθ 2 X θjX 2 r(¼; ±¼) = E E (θ ¡ ±¼(X)) = E E (θ ¡ ±¼(X)) : Thus, conveniently choosing either EθEXjθ or EX EθjX and using the properties of conditional expectation we have, θ Xjθ 2 θ Xjθ X θjX X θjX 2 r(¼; ±¼) = E E θ ¡ E E θ±¼(X) ¡ E E θ±¼(X) + E E ±¼(X) θ Xjθ 2 θ Xjθ X θjX X θjX 2 = E E θ ¡ E θ[E ±¼(X)] ¡ E ±¼(X)E θ + E E ±¼(X) θ Xjθ 2 θ X X θjX 2 = E E θ ¡ E θ ¢ θ ¡ E ±¼(X)±¼(X) + E E ±¼(X) = 0: Bayesians are not upset. To check for its unbiasedness, the Bayes estimator is averaged with respect to the model measure (Xjθ), and one of the Bayesian commandments is: Thou shall not average with respect to sample space, unless you have Bayesian design in mind. Even frequentist agree that insisting on unbiasedness can lead to bad estimators, and that in their quest to minimize the risk by trading off between variance and bias-squared a small dosage of bias can help. -

11. Parameter Estimation
11. Parameter Estimation Chris Piech and Mehran Sahami May 2017 We have learned many different distributions for random variables and all of those distributions had parame- ters: the numbers that you provide as input when you define a random variable. So far when we were working with random variables, we either were explicitly told the values of the parameters, or, we could divine the values by understanding the process that was generating the random variables. What if we don’t know the values of the parameters and we can’t estimate them from our own expert knowl- edge? What if instead of knowing the random variables, we have a lot of examples of data generated with the same underlying distribution? In this chapter we are going to learn formal ways of estimating parameters from data. These ideas are critical for artificial intelligence. Almost all modern machine learning algorithms work like this: (1) specify a probabilistic model that has parameters. (2) Learn the value of those parameters from data. Parameters Before we dive into parameter estimation, first let’s revisit the concept of parameters. Given a model, the parameters are the numbers that yield the actual distribution. In the case of a Bernoulli random variable, the single parameter was the value p. In the case of a Uniform random variable, the parameters are the a and b values that define the min and max value. Here is a list of random variables and the corresponding parameters. From now on, we are going to use the notation q to be a vector of all the parameters: Distribution Parameters Bernoulli(p) q = p Poisson(l) q = l Uniform(a,b) q = (a;b) Normal(m;s 2) q = (m;s 2) Y = mX + b q = (m;b) In the real world often you don’t know the “true” parameters, but you get to observe data. -

Bayes Estimator Recap - Example
Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Last Lecture . Biostatistics 602 - Statistical Inference Lecture 16 • What is a Bayes Estimator? Evaluation of Bayes Estimator • Is a Bayes Estimator the best unbiased estimator? . • Compared to other estimators, what are advantages of Bayes Estimator? Hyun Min Kang • What is conjugate family? • What are the conjugate families of Binomial, Poisson, and Normal distribution? March 14th, 2013 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 1 / 28 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 2 / 28 Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Recap - Bayes Estimator Recap - Example • θ : parameter • π(θ) : prior distribution i.i.d. • X1, , Xn Bernoulli(p) • X θ fX(x θ) : sampling distribution ··· ∼ | ∼ | • π(p) Beta(α, β) • Posterior distribution of θ x ∼ | • α Prior guess : pˆ = α+β . Joint fX(x θ)π(θ) π(θ x) = = | • Posterior distribution : π(p x) Beta( xi + α, n xi + β) | Marginal m(x) | ∼ − • Bayes estimator ∑ ∑ m(x) = f(x θ)π(θ)dθ (Bayes’ rule) | α + x x n α α + β ∫ pˆ = i = i + α + β + n n α + β + n α + β α + β + n • Bayes Estimator of θ is ∑ ∑ E(θ x) = θπ(θ x)dθ | θ Ω | ∫ ∈ Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 3 / 28 Hyun Min Kang Biostatistics 602 - Lecture 16 March 14th, 2013 4 / 28 Recap Bayes Risk Consistency Summary Recap Bayes Risk Consistency Summary . Loss Function Optimality Loss Function Let L(θ, θˆ) be a function of θ and θˆ.