The Terminator-Time Method and 3D Problem of Subionospheric
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

View and Print This Publication
@ SOUTHWEST FOREST SERVICE Forest and R U. S.DEPARTMENT OF AGRICULTURE P.0. BOX 245, BERKELEY, CALIFORNIA 94701 Experime Computation of times of sunrise, sunset, and twilight in or near mountainous terrain Bill 6. Ryan Times of sunrise and sunset at specific mountain- ous locations often are important influences on for- estry operations. The change of heating of slopes and terrain at sunrise and sunset affects temperature, air density, and wind. The times of the changes in heat- ing are related to the times of reversal of slope and valley flows, surfacing of strong winds aloft, and the USDA Forest Service penetration inland of the sea breeze. The times when Research NO& PSW- 322 these meteorological reactions occur must be known 1977 if we are to predict fire behavior, smolce dispersion and trajectory, fallout patterns of airborne seeding and spraying, and prescribed burn results. ICnowledge of times of different levels of illumination, such as the beginning and ending of twilight, is necessary for scheduling operations or recreational endeavors that require natural light. The times of sunrise, sunset, and twilight at any particular location depend on such factors as latitude, longitude, time of year, elevation, and heights of the surrounding terrain. Use of the tables (such as The 1 Air Almanac1) to determine times is inconvenient Ryan, Bill C. because each table is applicable to only one location. 1977. Computation of times of sunrise, sunset, and hvilight in or near mountainous tersain. USDA Different tables are needed for each location and Forest Serv. Res. Note PSW-322, 4 p. Pacific corrections must then be made to the tables to ac- Southwest Forest and Range Exp. -

Chapter 19 the Almanacs
CHAPTER 19 THE ALMANACS PURPOSE OF ALMANACS 1900. Introduction The Air Almanac was originally intended for air navigators, but is used today mostly by a segment of the Celestial navigation requires accurate predictions of the maritime community. In general, the information is similar to geographic positions of the celestial bodies observed. These the Nautical Almanac, but is given to a precision of 1' of arc predictions are available from three almanacs published and 1 second of time, at intervals of 10 minutes (values for annually by the United States Naval Observatory and H. M. the Sun and Aries are given to a precision of 0.1'). This Nautical Almanac Office, Royal Greenwich Observatory. publication is suitable for ordinary navigation at sea, but The Astronomical Almanac precisely tabulates celestial lacks the precision of the Nautical Almanac, and provides data for the exacting requirements found in several scientific GHA and declination for only the 57 commonly used fields. Its precision is far greater than that required by navigation stars. celestial navigation. Even if the Astronomical Almanac is The Multi-Year Interactive Computer Almanac used for celestial navigation, it will not necessarily result in (MICA) is a computerized almanac produced by the U.S. more accurate fixes due to the limitations of other aspects of Naval Observatory. This and other web-based calculators are the celestial navigation process. available from: http://aa.usno.navy.mil. The Navy’s The Nautical Almanac contains the astronomical STELLA program, found aboard all seagoing naval vessels, information specifically needed by marine navigators. contains an interactive almanac as well. -

The Golden Hour Refers to the Hour Before Sunset and After Sunrise
TheThe GoldenGolden HourHour The Golden Hour refers to the hour before sunset and after sunrise. Photographers agree that some of the very best times of day to take photos are during these hours. During the Golden Hours, the atmosphere is often permeated with breathtaking light that adds ambiance and interest to any scene. There can be spectacular variations of colors and hues ranging from subtle to dramatic. Even simple subjects take on an added glow. During the Golden Hours, take photos when the opportunity presents itself because light changes quickly and then fades away. 07:14:09 a.m. 07:15:48 a.m. Photographed about 60 seconds after previous photo. The look of a scene can vary greatly when taken at different times of the day. Scene photographed midday Scene photographed early morning SampleSample GoldenGolden HourHour photosphotos Top Tips for taking photos during the Golden Hours Arrive on the scene early to take test shots and adjust camera settings. Set camera to matrix or center-weighted metering. Use small apertures for maximizing depth-of-field. Select the lowest possible ISO. Set white balance to daylight or sunny day. When lighting is low, use a tripod with either a timed shutter release (self-timer) or a shutter release cable or remote. Taking photos during the Golden Hours When photographing the sun Don't stare into the sun, or hold the camera lens towards it for a very long time. Meter for the sky but don't include the sun itself. Composition tips: The horizon line should be above or below the center of the scene. -

Exploring Solar Cycle Influences on Polar Plasma Convection
Comparison of Terrestrial and Martian TEC at Dawn and Dusk during Solstices Angeline G. Burrell1 Beatriz Sanchez-Cano2, Mark Lester2, Russell Stoneback1, Olivier Witasse3, Marco Cartacci4 1Center for Space Sciences, University of Texas at Dallas 2Radio and Space Plasma Physics, University of Leicester 3European Space Agency, ESTEC – Scientific Support Office 4Istituto Nazionale di Astrofisica, Istituto di Astrofisica e Planetologia Spaziali 52nd ESLAB Symposium Outline • Motivation • Data and analysis – TEC sources – Data selection – Linear fitting • Results – Martian variations – Terrestrial variations – Similarities and differences • Conclusions Motivation • The Earth and Mars are arguably the most similar of the solar planets - They are both inner, rocky planets - They have similar axial tilts - They both have ionospheres that are formed primarily through EUV and X- ray radiation • Planetary differences can provide physical insights Total Electron Content (TEC) • The Global Positioning System • The Mars Advanced Radar for (GPS) measures TEC globally Subsurface and Ionosphere using a network of satellites and Sounding (MARSIS) measures ground receivers the TEC between the Martian • MIT Haystack provides calibrated surface and Mars Express TEC measurements • Mars Express has an inclination - Available from 1999 onward of 86.9˚ and a period of 7h, - Includes all open ground and allowing observations of all space-based sources locations and times - Specified with a 1˚ latitude by 1˚ • TEC is available for solar zenith longitude resolution with error estimates angles (SZA) greater than 75˚ Picardi and Sorge (2000), In: Proc. SPIE. Eighth International Rideout and Coster (2006) doi:10.1007/s10291-006-0029-5, 2006. Conference on Ground Penetrating Radar, vol. 4084, pp. 624–629. -

Planit! User Guide
ALL-IN-ONE PLANNING APP FOR LANDSCAPE PHOTOGRAPHERS QUICK USER GUIDES The Sun and the Moon Rise and Set The Rise and Set page shows the 1 time of the sunrise, sunset, moonrise, and moonset on a day as A sunrise always happens before a The azimuth of the Sun or the well as their azimuth. Moon is shown as thick color sunset on the same day. However, on lines on the map . some days, the moonset could take place before the moonrise within the Confused about which line same day. On those days, we might 3 means what? Just look at the show either the next day’s moonset or colors of the icons and lines. the previous day’s moonrise Within the app, everything depending on the current time. In any related to the Sun is in orange. case, the left one is always moonrise Everything related to the Moon and the right one is always moonset. is in blue. Sunrise: a lighter orange Sunset: a darker orange Moonrise: a lighter blue 2 Moonset: a darker blue 4 You may see a little superscript “+1” or “1-” to some of the moonrise or moonset times. The “+1” or “1-” sign means the event happens on the next day or the previous day, respectively. Perpetual Day and Perpetual Night This is a very short day ( If further north, there is no Sometimes there is no sunrise only 2 hours) in Iceland. sunrise or sunset. or sunset for a given day. It is called the perpetual day when the Sun never sets, or perpetual night when the Sun never rises. -

Here's Some Ideas
On that “Perfect Moment.” “Sometimes there’s that perfect moment when the crowd, the music, the energy of the room come together in a way that brings me to tears” John Legend. Covid-19 Safety Concerns The LCC executive advises against heading out right now. By staying home, you are protecting your life as well as the lives of others. If you are out and about though, remember to keep 2 meters apart, watch what you touch and wash your hands often (yeah, I know- I sound like your mom…). May 2020 Theme- Blue Hour. Definition: The blue hour is the period of twilight in the morning or evening, when the Sun is at a significant depth below the horizon and residual, indirect sunlight takes on a predominantly blue shade that is different from the blue shade visible during most of the day, which is caused by Rayleigh scattering. The requirement to have taken the picture at the Blue Hour has been suspended. Feel free to use post-production techniques in your editing software to add in the “Cool Blues.” Take out some of your old, Blue Hour images and work at enhancing them to best suit this theme. Here’s some ideas: Tim Shields critiques a number of pictures to describe what makes a great Blue Hour shot. Tim does a good job describing what works and what doesn’t. The video is about 15 minutes long but only the first 7 minutes is on the Blue Hour. Tim also touches on how some of the contributed photos could have been enhanced through simple steps in post production. -

Roadmap #84 Hardly Any Light ⏤ Which Means Much Slower Shutter Speeds As Well
BREAKFAST STOCK CLUB PREMIUM CHALLENGE #84 SEQUOIA CLUB Blue Hour By Marilyn Nieves Also known as the blue hour, twilight is what I call the magical hour of the day. As winter settles in and we experience shorter days, it’s the perfect time to have some fun with night photography. The blue hour comes twice a day. It’s called the blue “hour” but in reality, the average time frame is about 30 minutes, depending on your location. It happens just before sunrise and then again right after sunset. I typically go out to capture it in the evening as the sky’s blue deepens and you see hints of purple and magenta. As city lights turn on, their golden hues seem even more vibrant and eye- catching in contrast with the sky. No matter where you are, there’s just something wonderful and magical in blue hour images. It’s a sliver of the day that transforms everything we see. Twilight Images as Stock Blue hour images are not only eye- catching but they can create a mood of wonder, mystery, and exploration among viewers. Think of destinations from the perspective of the traveler and what would feel inviting and make you want to explore that place. Blue hour light can create some stunning stock images useful for travel related advertising projects. From a slightly more abstract point of view, with the aperture wide open to give you just a hint of the city, this image can be used in so many ways. For example, other than as a travel concept it can also be used as a broader conceptual business theme about looking towards the future and unlimited possibilities. -
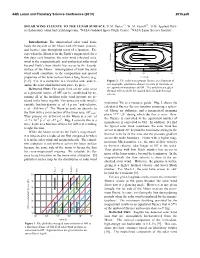
Solar Wind Fluence to the Lunar Surface
44th Lunar and Planetary Science Conference (2013) 2015.pdf SOLAR WIND FLUENCE TO THE LUNAR SURFACE. D. M. Hurley1,3, W. M. Farrell2,3, 1JHU Applied Phys- ics Laboratory ([email protected]), 2NASA Goddard Space Flight Center, 3NASA Lunar Science Institute. Monolayers delivered in one lunation Introduction: The unperturbed solar wind bom- 90 bards the dayside of the Moon with electrons, protons, 60 and heavier ions throughout most of a lunation. Ex- cept when the Moon is in the Earth’s magnetotail for a 30 few days each lunation, the solar wind (shocked solar 0 N. Latitude wind in the magnetosheath, and unshocked solar wind -30 beyond Earth’s bow shock) has access to the dayside -60 surface of the Moon. Investigations of how the solar -90 wind could contribute to the composition and optical 0 90 180 270 360 properties of the lunar surface have a long history (e.g. E. Longitude [1-7]. Yet, it is instructive to revisit this issue and ex- Figure 2. The solar wind proton fluence as a function of amine the solar wind interaction piece by piece. selenographic position is shown in terms of fractions of Delivered Flux: The upper limit on the solar wind an equivalent monolayer of OH. The solid lines neglect thermal effects while the dashed lines include thermal as a potential source of OH can be established by as- effects. suming all of the incident solar wind protons are re- tained in the lunar regolith. The quiescent solar wind is implanted 3He as a resource guide. Fig. 2 shows the variable, but has density, n, of ~5 p+cm-3 and velocity, calculated fluence for one lunation assuming a spheri- v, of ~350 km s-1. -

The American Air Almanac
THE AMERICAN AIR ALMANAC In 1933 the U.S. Naval Observatory prepared and published an air almanac planned especially for the aviator. This almanac, designed to eliminate many steps previously required for solving celestial sights,was enthusiastically received by airmen and led to the issuance of air almanacs by several foreign governments. Lack of sufficient appropriations prevented the Naval Observatory from continuing the publication of the American Air Almanac. However, coincident with the increased acceleration of aviation activities, funds were recently made available to resume publication of the Air Almanac. This publication will appear in issues covering periods of four months, the first issue being for the months of January, February, March, and April, 1941. It is expected that this issue will be available for sale early in December, 1940,through the Superintendent of Documents, Washington, D. C. All data for one day are concentrated on a single sheet. These include coordinates of the Sun, Moon, principal planets, and stars, as well as sunrise, sunset, moonrise, and moonset tables. Interpolation tables are placed adjacent to this daily sheet and so arranged as to be easily understood. Every effort has been made to shorten the number of operations required in working sights of heavenly bodies, an obvious saving of time as well as decreasing the chances for error in computation. At the time when the Aircraft Navigational Manual, H. O. Publication N° 216 was • prepared, the manuscript of the American Air Almanac was not available for use in illustrat ing the^chapter on Celestial Navigation. The values contained in the American Air Almanac, however, may readily be substituted for those taken from the American Nautical Almanac and used with even greater facility. -

Evening Or Morning: When Does the Biblical Day Begin?
Andrews University Seminary Studies, Vol. 46, No. 2, 201-214. Copyright © 2008 Andrews University Press. EVENING OR MORNING: WHEN DOES THE BIBLICAL DAY BEGIN? J. AM A ND A MCGUIRE Berrien Springs, Michigan Introduction There has been significant debate over when the biblical day begins. Certain biblical texts seem to indicate that the day begins in the morning and others that it begins in the evening. Scholars long believed that the day began at sunset, according to Jewish tradition. Jews begin their religious holidays in the evening,1 and the biblical text mandates that the two most important religious feasts, the Passover2 and the Day of Atonement,3 begin at sunset. However, in recent years, many scholars have begun to favor a different view: the day begins in the morning at sunrise. Although it may be somewhat foreign to the ancient Hebrew mind to rigidly define the day as a twenty-four-hour period that always begins and ends at the same time,4 the controversy has important implications for the modern reader. The question arises: When does the Sabbath begin and end? The purpose of this paper is to examine whether the day begins in the morning or in the evening by analyzing the sequence of events on the first day of creation (Gen 1:2-5), examining texts that are used to support both theories, and then determining how the evidence in these texts relates to the religious observances prescribed in the Torah. Because of time constraints, I do not explore the question of whether or not the days in Gen 1 are literal. -

Understanding Golden Hour, Blue Hour and Twilights
Understanding Golden Hour, Blue Hour and Twilights www.photopills.com Mark Gee proves everyone can take contagious images 1 Feel free to share this ebook © PhotoPills April 2017 Never Stop Learning The Definitive Guide to Shooting Hypnotic Star Trails How To Shoot Truly Contagious Milky Way Pictures A Guide to the Best Meteor Showers in 2017: When, Where and How to Shoot Them 7 Tips to Make the Next Supermoon Shine in Your Photos MORE TUTORIALS AT PHOTOPILLS.COM/ACADEMY Understanding How To Plan the Azimuth and Milky Way Using Elevation The Augmented Reality How to find How To Plan The moonrises and Next Full Moon moonsets PhotoPills Awards Get your photos featured and win $6,600 in cash prizes Learn more+ Join PhotoPillers from around the world for a 7 fun-filled days of learning and adventure in the island of light! Learn More We all know that light is the crucial element in photography. Understanding how it behaves and the factors that influence it is mandatory. For sunlight, we can distinguish the following light phases depending on the elevation of the sun: golden hour, blue hour, twilights, daytime and nighttime. Starting time and duration of these light phases depend on the location you are. This is why it is so important to thoughtfully plan for a right timing when your travel abroad. Predicting them is compulsory in travel photography. Also, by knowing when each phase occurs and its light conditions, you will be able to assess what type of photography will be most suitable for each moment. Understanding Golden Hour, Blue Hour and Twilights 6 “In almost all photography it’s the quality of light that makes or breaks the shot. -

The Above Are Lyrics Taken from the Tune Sunrise, Sunset —A Well-Known Song from the Theatrical Production Fiddler on the Roof
Yard and Garden - 02-02-2013 - Ted Griess / Extension Horticulture Assistant Sunrise, sunset Sunrise, sunset Swiftly flow the days. Seedlings turn overnight to sunflowers Blossoming even as we gaze. The above are lyrics taken from the tune Sunrise, Sunset —a well-known song from the theatrical production Fiddler on the Roof. Of late these lyrics have been bouncing around in my head, not because I’ve recently attended the theater; but, rather, I have been passionately observing the remarkable production Mother Nature has been providing us. I am reasonably sure this keen awareness is due to my dislike for winter and a longing for spring when I can again garden. As I arise in the dark each morning, I usually walk into my home office and check our outdoor thermometer. Observing how cold the outdoors temperature is, I generally utter a shivering “B-r-r” and head directly to our living room to light a fire in our fireplace. By the time a nice flame is flickering, Rita joins me with a hot cup of coffee and there we sit, enjoying the warmth, chatting and planning our day. Later, as the morning sun begins to rise above the horizon, I frequently find myself gazing out our windows to the east, marveling at the beautiful red and orange colors that streak across the gray-blue dawning sky. Sunrise in my backyard What a breath- taking sight it is, and how awe-struck I am. Fortunately, this amazing display often repeats itself near the end of the day— a miraculous spectacle we call sunset.