DOCSLIB.ORG

Gelfandsaul-Trigonometry.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Gelfandsaul-Trigonometry.Pdf For Madge Goldman who has done so much to bring so many people together I.M. Gelfand Mark Saul Trigonometry Birkhauser Boston • Basel • Berlin I.M. Gelfand Mark Saul Department of Mathematics Bronxville Schools Rutgers University Bronxville, NY 10708 Piscataway, NJ 08854-8019 U.S.A. U.S.A. Library of Congress Cataloging-in-Publication Data Gel'fand, I.M. (Izrail' Moiseevich) Trigonometry I I.M. Gel'fand, Mark Saul. p. em. ISBN 0-8176-3914-4 (alk. paper) I. Trigonometry, Plane. I. Saul, Mark E. II. Title. QA533.G45 1999 516.24'2-dc21 99-32245 CIP Printed on acid-free paper © 2001 I.M. Gelfand Birkhiiuser All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Birkhauser Boston, c/o Springer-Verlag New York, Inc., 175 Fifth Avenue, New York, NY 10010, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use of general descriptive names, trade names, trademarks, etc., in this publication, even if the former are not especially identified, is not to be taken as a sign that such names, as understood by the Trade Marks and Merchandise Marks Act, may accordingly be used freely by anyone. ISBN 0-8176-3914-4 SPIN 10536370 ISBN 3-7643-3914-4 Typeset in J.!\TEX by Martin Stock, Cambridge, MA Printed and bound by Hamilton Printing, Rensselaer, NY Printed in the United States of America 9 8 7 6 5 4 3 2 1 Contents Preface ix 0 Trigonometry 1 1 What is new about trigonometry? . 1 2 Right triangles . 6 3 The Pythagorean theorem . 7 4 Our best friends (among right triangles) 9 5 Our next best friends (among right triangles) . 10 6 Some standard notation . 12 1 Trigonometric Ratios in a Triangle 21 1 Definition of sin a . 21 2 Find the hidden sine . 24 3 The cosine ratio . 26 4 A relation between the sine and the cosine 28 5 A bit of notation . 28 6 Another relation between the sine and the cosine 29 7 Our next best friends (and the sine ratio) .. 30 8 What is the value of sin 90°? .......... 32 9 An exploration: How large can the sum be? .. 33 10 More exploration: How large can the product be? 34 11 More names for ratios . 35 2 Relations among Trigonometric Ratios 41 1 The sine and its relatives 41 2 Algebra or geometry? . 44 3 A remark about names 45 4 An identity crisis? .... 46 5 Identities with secant and cosecant 48 6 A lemma ..... 50 7 Some inequalities . 51 vi Contents 8 Calculators and tables . 52 9 Getting the degree measure of an angle from its sine . 53 10 Solving right triangles . 55 11 Shadows .............. 56 12 Another approach to the sine ratio 57 3 Relationships in a Triangle 67 1 Geometry of the triangle •••• 0 0 0 • 0 0 67 2 The congruence theorems and trigonometry 68 3 Sines and altitudes 69 4 Obtuse triangles . 70 5 The Law of Sines 71 6 The circumradius .,. 74 7 Area of a triangle 75 8 Two remarks 78 9 Law of cosines 78 4 Angles and Rotations 91 1 Measuring rotations . 0 •••••••• ' 91 2 Rotation and angles . 0 • 0 •••• 0 • 93 3 Trigonometric functions for all angles 94 4 Calculations with angles of rotations 98 5 Odd and even functions 0 •• 0 •• 0 101 5 Radian Measure 103 1 Radian measure for angles and rotations 103 2 Radian measure and distance . 109 3 Interlude: How to explain radian measure to your brother and sister . 113 4 Radian measure and calculators . 114 5 An important graph 115 6 Two small miracles 117 6 The Addition Formulas 123 1 More identities .. 123 2 The addition formulas . 125 3 Proofs of the addition formulas 126 4 A first beautiful proof . 127 5 A second beautiful proof .... ·130 Contents vii 7 Trigonometric Identities 139 1 Extending the identities . 139 2 The Principle of Analytic Continuation: Higher mathematics to the rescue . 139 3 Back to our identities . 141 4 A formula for tan (a+ {3) . 143 5 Double the angle . 145 6 Triple the angle . 148 7 Derivation of the formulas for sin a /2 and cos a /2 . 149 8 Another formula for tan aj2 151 9 Products to sums 152 10 Sums to products . 154 8 Graphs of Trigonometric Functions 173 1 Graphing the basic sine curve . 173 2 The period of the function y = sin x 175 3 Periods of other sinusoidal curves 176 4 The amplitude of a sinusoidal curve 178 5 Shifting the sine . 179 6 Shifting and stretching . 182 7 Some special shifts: Half-periods . 183 8 Graphing the tangent and cotangent functions 187 9 An important question about sums of sinusoidal functions . 188 10 Linear combinations of sines and cosines . 189 11 Linear combinations of sinusoidal curves with the same frequency . 192 12 Linear combinations of functions with different frequencies 194 13 Finding the period of a sum of sinusoidal curves with different periods . 196 14 A discovery of Monsieur Fourier . 197 9 Inverse Functions and Trigonometric Equations 207 1 Functions and Inverse Functions 207 2 Arcsin: The inverse function to sin 209 3 Graphing inverse functions . 214 4 Trigonometric equations . 217 5 A more general trigonometric equation . 220 6 More complicated trigonometric equations . 222 Preface In a .sense, trigonometry sits at the center of high school mathematics. It originates in the study of geometry when we investigate the ratios of sides in similar right triangles, or when we look at the relationship between a chord of a circle and its arc. It leads to a much deeper study of periodic functions, and of the so-called transcendental functions, which cannot be described using finite algebraic processes. It also has many applications to physics, astronomy, and other branches of science. It is a very old subject. Many of the geometric results that we now state in trigonometric terms were given a purely geometric exposition by Euclid. Ptolemy, an early astronomer, began to go beyond Euclid, using th~ geometry of the time to construct what we now call tables of values of trigonometric functions. Trigonometry is an important introduction to calculus, where one stud­ ies what mathematicians call analytic properties of functions. One of the goals of this book is to prepare you for a course in calculus by directing your attention away from particular values of a function to a study of the function as an object in itself. This way of thinking is useful not just in calculus, but in many mathematical situations. So trigonometry is a part of pre-calculus, and is related to other pre-calculus topics, such as exponential and logarithmic functions, and complex numbers. The interaction of these topics with trigonometry opens a whole new landscape of mathematical results. But each of these results is also important in its own right, without being "pre-" anything. We have tried to explain the beautiful results of trigonometry as simply and systematically as possible. In many cases we have found that simple problems have connections with profound and advanced ideas. Sometimes we have indicated these connections. In other cases we have left them for you to discover as you learn more about mathematics. X Preface About the exercises: We have tried to include a few problems of each "routine" type. If you need to work more such problems, they are easy to find. Most of our problems, however, are more challenging, or exhibit a new aspect of the technique or object under discussion. We have tried to make each exercise tell a little story about the mathematics, and have the stories build to a deep understanding. We will be happy if you enjoy this book and learn something from it. We enjoyed writing it, and learned a lot too. Acknowledgments The authors would like to thank Martin Stock, who took a very ragged manuscript and turned it into the book you are now holding. We also thank Santiago Samanca and the late Anneli Lax for their reading of the manu­ script and correction of several bad blunders. We thank Ann Kostant for her encouragement, support, and gift for organization. We thank the students of Bronxville High School for their valuable classroom feedback. Finally, 'We thank Richard Askey for his multiple readings of the manuscripts, for cor­ recting some embarrassing gaffes, and for making important suggestions that contributed significantly to the content of the book. Israel M. Gelfand Mark Saul March 20, 2001 Chapter 0 Trigonometry f. Gr. r p[y wvo- v triangle + - {tHp[a measurement. - Oxford English Dictionary In this chapter we will look at some results in geometry that set the stage for a study of trigonometry. 1 What is new about trigonometry? Two of the most basic figures studied in geometry are the triangle and the circle. Tngonometry will tell us more than we learned in geometry about each of these figures. For example, in geometry we learn that if we know the lengths of the three sides of a triangle, then the measures of its angles are completely determined1 (and, in fact, almost everything else about the triangle is de­ termined). But, except for a few very special triangles, geometry does not tell us how to compute the measures of the angles, given the measures of the sides. Example 1 The measures of the sides of a triangle are 6, 6, and 6 cen­ timeters.
Load more

Recommended publications
  • Simplification of Radical Expressions
    Simplification of Radical Expressions by B. F. Caviness (I) Computer Science Department lllinois Institute of Technology Chicago, lllinois and R. J. Fateman Computer Science Division Department of Electrical Engineering and Computer Sciences University of California at Berkeley Berkeley, California Abstract As is the case with all simplification problems there are three desirable attributes for In this paper we discuss the problem of any solution. First it is desirable to have a simplifying unnested radical expressions. We clean theoretical solution to the problem. Second describe an algorithm implemented in ~CSYMA that the algorithms to carry out the simplifications simplifies radical expressions and then follow should be as efficient as possible, and finally the this description with a formal treatment of the solution should have good human engineering features, problem. Theoretical computing times for some of i.e., the use and actions of the simplification the algorithms are briefly discussed as is related procedures should be as natural and transparent as work of other authors. possible. Unfortunately these three aspects of a solution are not usually compatible with each other I. Introduction and compromises and choices must be made. This is certainly the case for the simplification of radical In this paper we discuss the problem of expressions. Standard techniques from the theory simplifying unnested radical expressions. By of algebraic field extensions can be used to get a radical expressions we mean, roughly speaking, nice theoretical solution to the problem. However sums, differences, products, and quotients of the nice theoretical solution neither leads to fast rational functions raised to rational powers. algorithms nor possesses nice human engineering Thus we will be discussing algorithms for carrying features.
    [Show full text]
  • Construction Surveying Curves
    Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain.
    [Show full text]
  • And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
    9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • A Framework for a Public-Private Partnership to Increase The
    A national laboratory of the U.S. Department of Energy Office of Energy Efficiency & Renewable Energy National Renewable Energy Laboratory Innovation for Our Energy Future Enhancing Commercial Technical Report NREL/TP-110-40463 Outcomes from R&D May 2007 A Framework for a Public–Private Partnership to Increase the Yield of Federally Funded R&D Investments and Promote Economic Development L.M. Murphy Manager, Enterprise Development Programs National Renewable Energy Laboratory P. Jerde Executive Director Robert H. and Beverly A. Deming Center for Entrepreneurship, Leeds School of Business University of Colorado, Boulder L. Rutherford Venture Partner Vista Ventures R. Barone 2008 MS/MBA Candidate Department of Environmental Studies and Leeds School of Business University of Colorado, Boulder NREL is operated by Midwest Research Institute ● Battelle Contract No. DE-AC36-99-GO10337 Enhancing Commercial Technical Report NREL/TP-110-40463 Outcomes from R&D May 2007 A Framework for a Public–Private Partnership to Increase the Yield of Federally Funded R&D Investments and Promote Economic Development L.M. Murphy Manager, Enterprise Development Programs National Renewable Energy Laboratory P. Jerde Executive Director Robert H. and Beverly A. Deming Center for Entrepreneurship, Leeds School of Business University of Colorado, Boulder L. Rutherford Venture Partner Vista Ventures R. Barone 2008 MS/MBA Candidate Department of Environmental Studies and Leeds School of Business University of Colorado, Boulder Prepared under Task No. 1100.1000 National Renewable Energy Laboratory 1617 Cole Boulevard, Golden, Colorado 80401-3393 303-275-3000 • www.nrel.gov Operated for the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy by Midwest Research Institute • Battelle Contract No.
    [Show full text]
  • From the Theorem of the Broken Chord to the Beginning of the Trigonometry
    From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction.
    [Show full text]
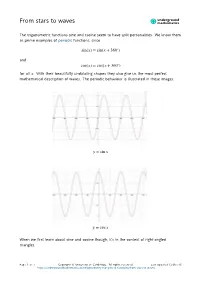
  • From Stars to Waves Mathematics
    underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge.
    [Show full text]
  • Group Looks to Save Brandywine's Deli
    407-740-0401 www.FirstColonyBank.net TAX DEFERRED NEW Dermatology Office! 3.35% FIXED ANNUITY RATE FOR 5 YEARS. THE NATIONAL 5 YEAR CD RATE IS 1.34% 407-599-SKIN (7546) *Waive co-payment up to $25 • No referral needed Your Real Hometown Bank Bob Adams • Accepting all insurances On Hwy 17-92 in Maitland 451 Maitland Ave, Altamonte Springs, FL 32701 Dr. John Cottam Dr. Ross Wheeler Member FDIC 407-644-6646 wpmobserver.com Thursday, April 12, 2012 50¢+ tax Calendar The Doggie Art Festival is this weekend, as well as the Maitland Art Festival and Culture & Cocktails. Page 10 Group looks to save Brandywine’s Deli ANDY CEBALLOS Observer Homes Observer Staff The existing home market in Orange Sandy Phillips started meet- and Seminole counties continued to ing at Brandywine’s Deli in Win- show signs of improvement last year. ter Park with friends from Rollins College in 1987. Page 20 For 25 years, it’s been a weekly Friday afternoon hangout, where the Oviedo resident and her friends and former colleagues gather to share laughs and sto- ries over beer, wine and snacks at the end of the workweek. But with the announced clos- ing of Brandywine’s Deli, she has found herself searching for Stop by and say goodbye to Brandywine’s answers as to why it has to close, Deli, 505 N. Park Ave., before it likely shuts and is taking her case straight to its doors forever on Saturday, April 28. the deli’s landlord. Phillips has mailed a peti- Lifestyles PHOTO BY ANDY CEBALLOS— THE OBSERVER The Florida Film Festival, which kicks tion signed by 325 individuals to landlord Wayne Roberts of This group of former Rollins colleagues and friends has eaten at Brandywine’s Deli every Friday for 25 years.
    [Show full text]
  • Lesson 2: Circles, Chords, Diameters, and Their Relationships
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first.
    [Show full text]
  • 11.4 Arcs and Chords
    Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter.
    [Show full text]
  • Simplifying Square Roots of Square Roots by Denesting 63
    4 Simplifying Square Ro ots of Square Ro ots by Denesting David J. Je rey Alb ert D. Rich The UniversityofWestern Ontario Soft Warehouse, Inc. Abstract: We discuss why it is imp ortant to try to simplify the square ro ot of an expression containing other square ro ots, and we give rules for doing this when it is p ossible. The square ro ot of an expression containing nth ro ots is also considered brie y. This article, in addition to treating a sp eci c mathematical topic, shows some of the steps that develop ers must take when writing computer algebra systems. 4.1 Intro duction p p 3 1 2 and 5 are called surds [Chrystal64, Hall88]. The more general Numb ers suchas terms radical and algebraic number are also used, but surd is the most sp eci c. It is 2 avenerable term that has b een revived for use in computer systems . Given p ositive n integers n and k , the unique p ositive real ro ot of the equation x = k will b e denoted p n k and called a surd. Most b o oks [Chrystal64, Hall88]allow k to b e a p ositive rational numb er, and there is no great di erence in principle if we accept that generalization; in this article, however, all the examples use integers. Another p ointofvariation is p p 8or2 2; here we the treatment of p erfect-p ower factors, i.e., whether one writes use whichever form is more convenient. The term radical may b e familiar to some readers from the common phrase `solvable in terms of radicals', which is used whenever a textb o ok discusses the ro ots of a p olynomial [Dickson26].
    [Show full text]
  • Continued Radicals Jamie Johnson Western Kentucky University
    Western Kentucky University TopSCHOLAR® Masters Theses & Specialist Projects Graduate School 2005 Continued Radicals Jamie Johnson Western Kentucky University Follow this and additional works at: http://digitalcommons.wku.edu/theses Part of the Geometry and Topology Commons Recommended Citation Johnson, Jamie, "Continued Radicals" (2005). Masters Theses & Specialist Projects. Paper 240. http://digitalcommons.wku.edu/theses/240 This Thesis is brought to you for free and open access by TopSCHOLAR®. It has been accepted for inclusion in Masters Theses & Specialist Projects by an authorized administrator of TopSCHOLAR®. For more information, please contact [email protected]. CONTINUED RADICALS A Thesis Presented to The Faculty of the Department of Mathematics Western Kentucky University Bowling Green, Kentucky In Partial Fulfillment Of the Requirements for the Degree Master of Science By Jamie Johnson May, 2005 CONTINUED RADICALS Date Recommended _____12/10/04_____ Dr. Tom Richmond, Chair Dr. John Spraker Dr. Daniel C. Biles Elmer Gray, Dean, Graduate Studies and Research, May 4, 2005 Contents Title page i Signatures ii Table of contents iii Abstract iv Chapter 1. Foundations and Motivations 1 Chapter 2. Introduction 5 Chapter 3. Continued radicals with nonzero terms 9 Chapter 4. Representation allowing 0 as a term 16 Chapter 5. Continued radicals whose terms assume only two values 24 Chapter 6. Further Results 26 6.1. Periodic Representations 26 6.2. A Pattern 28 6.3. Computer Generated Partial Representations 29 Bibliography 35 iii CONTINUED RADICALS Name: Jamie Johnson Date: May, 2005 Pages: 35 Directed by Dr. Tom Richmond Department of Mathematics Western Kentucky University Abstract √ If a1, a2, . , an are nonnegative real numbers and fj(x) = aj + x, then f1 ◦f2 ◦· · ·◦ fn(0) is a nested radical with terms a1, .
    [Show full text]