Reducing Quantization Error by Matching Pseudoerror Statistics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Suburban Noise Control with Plant Materials and Solid Barriers
Suburban Noise Control with Plant Materials and Solid Barriers by DAVID I. COOK and DAVID F. Van HAVERBEKE, respectively professor of engineering mechanics, University of Nebraska, Lin- coln; and silviculturist, USDA Forest Service, Rocky Mountain Forest and Range Experiment Station, Fort Collins, Colo. ABSTRACT.-Studies were conducted in suburban settings with specially designed noise screens consisting of combinations of plant inaterials and solid barriers. The amount of reduction in sound level due to the presence of the plant materials and barriers is re- ported. Observations and conclusions for the measured phenomenae are offered, as well as tentative recommendations for the use of plant materials and solid barriers as noise screens. YOUR$50,000 HOME IN THE SUB- relocated truck routes, and improved URBS may be the object of an in- engine muffling can be helpful. An al- vasion more insidious than termites, and ternative solution is to create some sort fully as damaging. The culprit is noise, of barrier between the noise source and especially traffic noise; and although it the property to be protected. In the will not structurally damage your house, Twin Cities, for instance, wooden walls it will cause value depreciation and dis- up to 16 feet tall have been built along comfort for you. The recent expansion Interstate Highways 35 and 94. Al- of our national highway systems, and though not esthetically pleasing, they the upgrading of arterial streets within have effectively reduced traffic noise, the city, have caused widespread traffic- and the response from property owners noise problems at residential properties. has been generally favorable. -

Realisation of the First Sub Shot Noise Wide Field Microscope
Realisation of the first sub shot noise wide field microscope Nigam Samantaray1,2, Ivano Ruo-Berchera1, Alice Meda1, , Marco Genovese1,3 1 INRIM, Strada delle Cacce 91, I-10135 Torino, ∗Italy 2 Politecnico di Torino, Corso Duca degli Abruzzi, 24 - I-10129 Torino, Italy and 3 INFN, Via P. Giuria 1, I-10125 Torino, Italy ∗ ∗ Correspondence: Alice Meda, Email: [email protected], Tel: +390113919245 In the last years several proof of principle experiments have demonstrated the advantages of quantum technologies respect to classical schemes. The present challenge is to overpass the limits of proof of principle demonstrations to approach real applications. This letter presents such an achievement in the field of quantum enhanced imaging. In particular, we describe the realization of a sub-shot noise wide field microscope based on spatially multi-mode non-classical photon number correlations in twin beams. The microscope produces real time images of 8000 pixels at full resolution, for (500µm)2 field-of-view, with noise reduced to the 80% of the shot noise level (for each pixel), suitable for absorption imaging of complex structures. By fast post-elaboration, specifically applying a quantum enhanced median filter, the noise can be further reduced (less than 30% of the shot noise level) by setting a trade-off with the resolution, demonstrating the best sensitivity per incident photon ever achieved in absorption microscopy. Keywords: imaging, sub shot noise, microscopy, parametric down conversion 1 INTRODUCTION Sensitivity in standard optical imaging and sensing, the ones exploiting classical illuminating fields, is fundamentally lower bounded by the shot noise, the inverse square root of the number of photons used. -

Noise Reduction Technologies for Turbofan Engines
NASA/TM—2007-214495 Noise Reduction Technologies for Turbofan Engines Dennis L. Huff Glenn Research Center, Cleveland, Ohio September 2007 NASA STI Program . in Profile Since its founding, NASA has been dedicated to the • CONFERENCE PUBLICATION. Collected advancement of aeronautics and space science. The papers from scientific and technical NASA Scientific and Technical Information (STI) conferences, symposia, seminars, or other program plays a key part in helping NASA maintain meetings sponsored or cosponsored by NASA. this important role. • SPECIAL PUBLICATION. Scientific, The NASA STI Program operates under the auspices technical, or historical information from of the Agency Chief Information Officer. It collects, NASA programs, projects, and missions, often organizes, provides for archiving, and disseminates concerned with subjects having substantial NASA’s STI. The NASA STI program provides access public interest. to the NASA Aeronautics and Space Database and its public interface, the NASA Technical Reports Server, • TECHNICAL TRANSLATION. English- thus providing one of the largest collections of language translations of foreign scientific and aeronautical and space science STI in the world. technical material pertinent to NASA’s mission. Results are published in both non-NASA channels and by NASA in the NASA STI Report Series, which Specialized services also include creating custom includes the following report types: thesauri, building customized databases, organizing and publishing research results. • TECHNICAL PUBLICATION. Reports of completed research or a major significant phase For more information about the NASA STI of research that present the results of NASA program, see the following: programs and include extensive data or theoretical analysis. Includes compilations of significant • Access the NASA STI program home page at scientific and technical data and information http://www.sti.nasa.gov deemed to be of continuing reference value. -

Journey to a Quiet Night
QUIET NIGHT TOOLKIT Journey to a Quiet Night Strategies to Reduce Hospital Noise and Promote Healing Patient responses to the HCAHPS survey of experience consistently identify noise at night as a dissatisfier in their hospital stay. Only 51% of patients surveyed following discharge from a California hospital report that their hospital room was always quiet at night, compared to 62% of patients nationally. Noise at night is our greatest challenge to create a healing environment of care. Hospitals that have successfully improved this dimension of care have used a few common strategies: informed staff behavior modification, mechanical noise mitigation, environmental noise mitigation, and real time data to drive changes. Drivers for Improvement in Hospital Noise • Educate staff about effects of noise on patient healing Informed Behavior • Engage staff in remediation plan development Modifi cation • Monitor noise in real time HCAHPS Score for “Always Quiet at Night” • “Quiet kits” for patients Mechanical above national average of • Equipment repair Mitigation • Noise absorbing panels or curtains in high traffi c areas AIM • Establish “quiet hours” Environmental 62% • Visual cues, such as signs and dimmed lights at night in patient care areas Mitigation • Utilize white noise options Real Time • Develop system of real time alerts based on patient/family input/feedback Data Learning • Real time reporting mechanism with feedback loop Informed behavior Modifi cation As health care providers, it is imperative that we understand and help to provide our patients with an environment that is optimized for healing. Staff members must be educated about the effects that noise from talking, equipment and other activities has on patients’ healing in the hospital. -

Effect of Noise Type and Signal-To-Noise Ratio on the Effectiveness of Noise Reduction Algorithm in Hearing Aids: an Acoustical Perspective
Global Journal of Otolaryngology ISSN 2474-7556 Research Article Glob J Otolaryngol - Volume 5 Issue 2 March 2017 Copyright © All rights are reserved by Sharath Kumar KS DOI: 10.19080/GJO.2017.05.555658 Effect of Noise Type and Signal-to-Noise Ratio on the Effectiveness of Noise Reduction Algorithm in Hearing Aids: An Acoustical Perspective Sharath Kumar KS* and Manjula P Department of Audiology, All India Institute of Speech and Hearing (AIISH), University of Mysuru, India Submission: March 05, 2016; Published: March 16, 2017 *Corresponding author: Sharath Kumar KS, Department of Audiology (New JC block), Manasagangotri, AIISH, Mysuru - 570 006, Karnataka, India, Tel: ; Email: Second author: Manjula P, Professor of Audiology, Department of Audiology, Manasagangotri, AIISH, Mysuru - 570 006 India, Karnataka, Tel: ; Email: Abstract Purpose: acoustical measures. The study evaluated factors that influence the effectiveness of noise reduction (NR) algorithm in hearing aids, through Methods: Factorial design was employed. Study sample: The output from hearing aid, with and without NR at three signal-to-noise Qualityratios (SNR) (PESQ). with five types of noise, was recorded. The effect of noise reduction was studied through objective measures such as Waveform Amplitude Distribution Analysis - Signal-to-Noise Ratio (WADA-SNR), Envelope Difference Index (EDI), and Perceptual Evaluation of Speech Results: The results revealed that when NR was enabled, it was effective in reducing the noise. However, when speech was presented in the presenceConclusion: of noise, the NR was effective in enhancing certain acoustic parameters of speech; like signal-to-noise ratio and envelope. changes in the output of the hearing aid with and without NR processing. -

Noise Reduction Using Active Vibration Control Methods in CAD/CAM Dental Milling Machines
applied sciences Article Noise Reduction Using Active Vibration Control Methods in CAD/CAM Dental Milling Machines Eun-Sung Song 1 , Young-Jun Lim 2,* , Bongju Kim 1 and Jeffery Sungjae Mun 3 1 Clinical Translational Research Center for Dental Science, Seoul National University Dental Hospital, Seoul 03080, Korea; [email protected] (E.-S.S.); [email protected] (B.K.) 2 Department of Prosthodontics and Dental Research Institute, School of Dentistry, Seoul National University, Seoul 03080, Korea 3 Department of Biology, Swarthmore College, Swarthmore, PA 19081, USA; [email protected] * Correspondence: [email protected]; Tel.: +82-02-2072-2040 Received: 28 February 2019; Accepted: 8 April 2019; Published: 12 April 2019 Abstract: Used in close proximity to dental practitioners, dental tools and devices, such as hand pieces, have been a possible risk factor to hearing loss due to the noises they produce. Recently, additional technologies such as CAD/CAM (Computer Aided Design/Computer Aided Manufacturing) milling machines have been used in the dental environment and have emerged as a new contributing noise source. This has created an issue in fostering a pleasant hospital environment. Currently, because of issues with installing and manufacturing noise-reducing products, the technology is impractical and insufficient relative to its costly nature. In this experiment, in order to create a safe working environment, we hoped to analyze the noise produced and determine a practical method to attenuate the noises coming from CAD/CAM dental milling machines. In this research, the cause for a noise and the noise characteristics were analyzed by observing and measuring the sound from a milling machine and the possibility of reducing noise in an experimental setting was examined using a noise recorded from a real milling machine. -
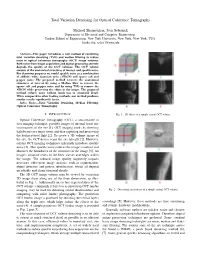
Total Variation Denoising for Optical Coherence Tomography
Total Variation Denoising for Optical Coherence Tomography Michael Shamouilian, Ivan Selesnick Department of Electrical and Computer Engineering, Tandon School of Engineering, New York University, New York, New York, USA fmike.sha, [email protected] Abstract—This paper introduces a new method of combining total variation denoising (TVD) and median filtering to reduce noise in optical coherence tomography (OCT) image volumes. Both noise from image acquisition and digital processing severely degrade the quality of the OCT volumes. The OCT volume consists of the anatomical structures of interest and speckle noise. For denoising purposes we model speckle noise as a combination of additive white Gaussian noise (AWGN) and sparse salt and pepper noise. The proposed method recovers the anatomical structures of interest by using a Median filter to remove the sparse salt and pepper noise and by using TVD to remove the AWGN while preserving the edges in the image. The proposed method reduces noise without much loss in structural detail. When compared to other leading methods, our method produces similar results significantly faster. Index Terms—Total Variation Denoising, Median Filtering, Optical Coherence Tomography I. INTRODUCTION Fig. 1. 2D slices of a sample retinal OCT volume. Optical Coherence Tomography (OCT), a non-invasive in vivo imaging technique, provides images of internal tissue mi- crostructures of the eye [1]. OCT imaging works by directing light beams at a target tissue and then capturing and processing the backscattered light [2]. To create a 3D volume image of the eye, the OCT device scans the eye laterally [2]. However, current OCT imaging techniques inherently introduce speckle noise [3]. -

Noise Reduction of EEG Signals Using Autoencoders Built Upon GRU Based RNN Layers
Technological University Dublin ARROW@TU Dublin Dissertations School of Computer Sciences 2020-02-01 Noise Reduction of EEG Signals Using Autoencoders Built Upon GRU based RNN Layers Esra Aynali Technological University Dublin Follow this and additional works at: https://arrow.tudublin.ie/scschcomdis Part of the Artificial Intelligence and Robotics Commons Recommended Citation Aynali, E. (2020). Noise Reduction of EEG Signals Using Autoencoders Built Upon GRU based RNN Layers. Dissertation. Dublin: Technological University Dublin. This Dissertation is brought to you for free and open access by the School of Computer Sciences at ARROW@TU Dublin. It has been accepted for inclusion in Dissertations by an authorized administrator of ARROW@TU Dublin. For more information, please contact [email protected], [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License Noise Reduction of EEG Signals Using Autoencoders Built Upon GRU based RNN Layers Esra Aynalı A dissertation submitted in partial fulfilment of the requirements of Technological University Dublin for the degree of M.Sc. in Computer Science (Data Analytics) January 2020 I certify that this dissertation which I now submit for examination for the award of MSc in Computing (Data Analytics), is entirely my own work and has not been taken from the work of others save and to the extent that such work has been cited and acknowledged within the test of my work. This dissertation was prepared according to the regulations for postgraduate study of the Technological University Dublin and has not been submitted in whole or part for an award in any other Institute or University. -

Performance of Analog Nonlinear Filtering for Impulsive Noise Mitigation in OFDM-Based PLC Systems
Performance of Analog Nonlinear Filtering for Impulsive Noise Mitigation in OFDM-based PLC Systems Reza Barazidehy, Balasubramaniam Natarajany, Alexei V. Nikitiny;∗, Ruslan L. Davidchack z y Department of Electrical and Computer Engineering, Kansas State University, Manhattan, KS, USA. ∗ Nonlinear Corp., Wamego, KS 66547, USA. z Dept. of Mathematics, U. of Leicester, Leicester, LE1 7RH, UK. Email:frezabarazideh,[email protected], [email protected], [email protected] Abstract—Asynchronous and cyclostationary impulsive noise electrical devices connected to the powerlines and coupled can severely impact the bit-error-rate (BER) of OFDM-based to the grid via conduction and radiation is a major issue powerline communication systems. In this paper, we analyze in PLC [5]. Due to its technogenic (man-made) nature, this an adaptive nonlinear analog front end filter that mitigates various types of impulsive noise without detrimental effects such noise is typically non-Gaussian and impulsive, as has been as self-interference and out-of-band power leakage caused by verified by field measurements. Therefore, PLC noise can be other nonlinear approaches like clipping and blanking. Our modelled as combination of two terms: thermal noise which proposed Adaptive Nonlinear Differential Limiter (ANDL) is is assumed to be additive white Gaussian noise (AWGN), and constructed from a linear analog filter by applying a feedback- the impulsive noise that may be synchronous or asynchronous based nonlinearity, controlled by a single resolution parameter. We present a simple practical method to find the value of this relative to the main frequency [6]. It is observed that the resolution parameter that ensures the mitigation of impulsive primary noise component in broadband PLC (BB-PLC) [7], [8] without impacting the desired OFDM signal. -

Reducing ADC Quantization Noise
print | close Reducing ADC Quantization Noise Microwaves and RF Richard Lyons Randy Yates Fri, 20050617 (All day) Two techniques, oversampling and dithering, have gained wide acceptance in improving the noise performance of commercial analogtodigital converters. Analogtodigital converters (ADCs) provide the vital transformation of analog signals into digital code in many systems. They perform amplitude quantization of an analog input signal into binary output words of finite length, normally in the range of 6 to 18 b, an inherently nonlinear process. This nonlinearity manifests itself as wideband noise in the ADC's binary output, called quantization noise, limiting an ADC's dynamic range. This article describes the two most popular methods for improving the quantization noise performance in practical ADC applications: oversampling and dithering. Related Finding Ways To Reduce Filter Size Matching An ADC To A Transformer Tunable Oscillators Aim At Reduced Phase Noise LargeSignal Approach Yields LowNoise VHF/UHF Oscillators To understand quantization noise reduction methods, first recall that the signaltoquantizationnoise ratio, in dB, of an ideal Nbit ADC is SNRQ = 6.02N + 4.77 + 20log10 (LF) dB, where: LF = the loading factor measure of the ADC's input analog voltage level. (A derivation of SNRQ is provided in ref. 1.) Parameter LF is defined as the analog input rootmeansquare (RMS) voltage divided by the ADC's peak input voltage. When an ADC's analog input is a sinusoid driven to the converter's fullscale voltage, LF = 0.707. In that case, the last term in the SNRQ equation becomes −3 dB and the ADC's maximum output signaltonoise ratio is SNRQmax = 6.02N + 4.77 −3 = 6.02N + 1.77 dB. -

Recurrent Neural Networks for Noise Reduction in Robust ASR
Recurrent Neural Networks for Noise Reduction in Robust ASR Andrew L. Maas1, Quoc V. Le1, Tyler M. O’Neil1, Oriol Vinyals2, Patrick Nguyen3, Andrew Y. Ng1 1Computer Science Department, Stanford University, CA, USA 2EECS Department, University of California - Berkeley, Berkeley, CA, USA 3Google, Inc., Mountain View, CA, USA [amaas,quocle,toneil]@cs.stanford.edu, [email protected], [email protected], [email protected] Abstract models and experimented with simple noise conditions – often a single background noise environment. Recent work on deep neural networks as acoustic mod- Our novel approach applies large neural network els for automatic speech recognition (ASR) have demon- models with several hidden layers and temporally recur- strated substantial performance improvements. We intro- rent connections. Such deep models should better capture duce a model which uses a deep recurrent auto encoder the complex relationships between noisy and clean utter- neural network to denoise input features for robust ASR. ances in data with many noise environments and noise The model is trained on stereo (noisy and clean) audio levels. In this way, our work shares underlying princi- features to predict clean features given noisy input. The ples with deep neural net acoustic models, which recently model makes no assumptions about how noise affects the yielded substantial improvements in ASR [5]. We exper- signal, nor the existence of distinct noise environments. iment with a reasonably large set of background noise Instead, the model can learn to model any type of distor- environments and demonstrate the importance of models tion or additive noise given sufficient training data. We with many hidden layers when learning a denoising func- demonstrate the model is competitive with existing fea- tion. -

Improving the Healing Environment in University of Michigan Hospital Through Noise Reduction and Masking Techniques
Improving the Healing Environment in University of Michigan Hospital through Noise Reduction and Masking Techniques Final Report Prepared For: Mr. Chris Schlaps, Planning and Development Project Manager University of Michigan Health System Prof. Harvey Bell, Co-Director of Multidisciplinary Program University of Michigan Dr. Amy Cohn, Arthur F. Thurnau Associate Professor University of Michigan Prepared By: Matthew DiTullio, Hospital Sound Analysis Team Member Tori Ranger, Hospital Sound Analysis Team Member Multidisciplinary Design Program Project Team: Keegan Cisowski, Hospital Sound Analysis Team Member Matthew DiTullio, Hospital Sound Analysis Team Member Tori Ranger, Hospital Sound Analysis Team Member Multidisciplinary Design Program Date: December 13th, 2012 ! Table of Contents Executive Summary 1 Current Situation and Task 1 Methods 1 Findings 2 Conclusions and Recommendations 3 Introduction 4 Background 4 Key Issues 5 Goals and Objectives 5 Project Scope 6 Pre-Implementation Methods and Findings 6 Literature Search 6 Benchmarking 7 Sound Inventory 7 Patient Surveys 8 Implementation Methods and Findings 11 Quiet Hours 11 Staff Support Awareness 12 White Noise 13 Conclusions 14 Recommendations 14 Expected Impact 15 Appendix A: Pre-Implementation HSAT Patient Survey 16 Appendix B: Post-Implementation HSAT Patient Survey 18 Appendix C: HSAT Staff Survey 20 Attachment A: Buxton Article 22 Attachment B: World Health Organization Article 33 Attachment C: Neergaard Article 35 ii! ! ! List of Figures and Tables Table 1: Average frequencies