Drawing the Line Between Kinematics and Dynamics in Special Relativity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

From Relativistic Time Dilation to Psychological Time Perception
From relativistic time dilation to psychological time perception: an approach and model, driven by the theory of relativity, to combine the physical time with the time perceived while experiencing different situations. Andrea Conte1,∗ Abstract An approach, supported by a physical model driven by the theory of relativity, is presented. This approach and model tend to conciliate the relativistic view on time dilation with the current models and conclusions on time perception. The model uses energy ratios instead of geometrical transformations to express time dilation. Brain mechanisms like the arousal mechanism and the attention mechanism are interpreted and combined using the model. Matrices of order two are generated to contain the time dilation between two observers, from the point of view of a third observer. The matrices are used to transform an observer time to another observer time. Correlations with the official time dilation equations are given in the appendix. Keywords: Time dilation, Time perception, Definition of time, Lorentz factor, Relativity, Physical time, Psychological time, Psychology of time, Internal clock, Arousal, Attention, Subjective time, Internal flux, External flux, Energy system ∗Corresponding author Email address: [email protected] (Andrea Conte) 1Declarations of interest: none Preprint submitted to PsyArXiv - version 2, revision 1 June 6, 2021 Contents 1 Introduction 3 1.1 The unit of time . 4 1.2 The Lorentz factor . 6 2 Physical model 7 2.1 Energy system . 7 2.2 Internal flux . 7 2.3 Internal flux ratio . 9 2.4 Non-isolated system interaction . 10 2.5 External flux . 11 2.6 External flux ratio . 12 2.7 Total flux . -

Using Time As a Sustainable Tool to Control Daylight in Space
USING TIME AS A SUSTAINABLE TOOL TO CONTROL DAYLIGHT IN SPACE Creating the Chronoform SAMER EL SAYARY Beirut Arab University and Alexandria University, Egypt [email protected] Abstract. Just as Einstein's own Relativity Theory led Einstein to reject time, Feynman’s Sum over histories theory led him to describe time simply as a direction in space. Many artists tried to visualize time as Étienne-Jules Marey when he invented the chronophotography. While the wheel of development of chronophotography in the Victorian era had ended in inventing the motion picture, a lot of research is still in its earlier stages regarding the time as a shaping media for the architectural form. Using computer animation now enables us to use time as a flexible tool to be stretched and contracted to visualize the time dilation of the Einstein's special relativity. The presented work suggests using time as a sustainable tool to shape the generated form in response to the sun movement to control the amount of daylighting entering the space by stretching the time duration and contracting time frames at certain locations of the sun trajectory along a summer day to control the amount of daylighting in the morning and afternoon versus the noon time. INTRODUCTION According to most dictionaries (Oxford, 2011; Collins, 2011; Merriam- Webster, 2015) Time is defined as a nonspatial continued progress of unlimited duration of existence and events that succeed one another ordered in the past, present, and future regarded as a whole measured in units such as minutes, hours, days, months, or years. -

Physics 200 Problem Set 7 Solution Quick Overview: Although Relativity Can Be a Little Bewildering, This Problem Set Uses Just A
Physics 200 Problem Set 7 Solution Quick overview: Although relativity can be a little bewildering, this problem set uses just a few ideas over and over again, namely 1. Coordinates (x; t) in one frame are related to coordinates (x0; t0) in another frame by the Lorentz transformation formulas. 2. Similarly, space and time intervals (¢x; ¢t) in one frame are related to inter- vals (¢x0; ¢t0) in another frame by the same Lorentz transformation formu- las. Note that time dilation and length contraction are just special cases: it is time-dilation if ¢x = 0 and length contraction if ¢t = 0. 3. The spacetime interval (¢s)2 = (c¢t)2 ¡ (¢x)2 between two events is the same in every frame. 4. Energy and momentum are always conserved, and we can make e±cient use of this fact by writing them together in an energy-momentum vector P = (E=c; p) with the property P 2 = m2c2. In particular, if the mass is zero then P 2 = 0. 1. The earth and sun are 8.3 light-minutes apart. Ignore their relative motion for this problem and assume they live in a single inertial frame, the Earth-Sun frame. Events A and B occur at t = 0 on the earth and at 2 minutes on the sun respectively. Find the time di®erence between the events according to an observer moving at u = 0:8c from Earth to Sun. Repeat if observer is moving in the opposite direction at u = 0:8c. Answer: According to the formula for a Lorentz transformation, ³ u ´ 1 ¢tobserver = γ ¢tEarth-Sun ¡ ¢xEarth-Sun ; γ = p : c2 1 ¡ (u=c)2 Plugging in the numbers gives (notice that the c implicit in \light-minute" cancels the extra factor of c, which is why it's nice to measure distances in terms of the speed of light) 2 min ¡ 0:8(8:3 min) ¢tobserver = p = ¡7:7 min; 1 ¡ 0:82 which means that according to the observer, event B happened before event A! If we reverse the sign of u then 2 min + 0:8(8:3 min) ¢tobserver 2 = p = 14 min: 1 ¡ 0:82 2. -

Speed Limit: How the Search for an Absolute Frame of Reference in the Universe Led to Einstein’S Equation E =Mc2 — a History of Measurements of the Speed of Light
Journal & Proceedings of the Royal Society of New South Wales, vol. 152, part 2, 2019, pp. 216–241. ISSN 0035-9173/19/020216-26 Speed limit: how the search for an absolute frame of reference in the Universe led to Einstein’s equation 2 E =mc — a history of measurements of the speed of light John C. H. Spence ForMemRS Department of Physics, Arizona State University, Tempe AZ, USA E-mail: [email protected] Abstract This article describes one of the greatest intellectual adventures in the history of mankind — the history of measurements of the speed of light and their interpretation (Spence 2019). This led to Einstein’s theory of relativity in 1905 and its most important consequence, the idea that matter is a form of energy. His equation E=mc2 describes the energy release in the nuclear reactions which power our sun, the stars, nuclear weapons and nuclear power stations. The article is about the extraordinarily improbable connection between the search for an absolute frame of reference in the Universe (the Aether, against which to measure the speed of light), and Einstein’s most famous equation. Introduction fixed speed with respect to the Aether frame n 1900, the field of physics was in turmoil. of reference. If we consider waves running IDespite the triumphs of Newton’s laws of along a river in which there is a current, it mechanics, despite Maxwell’s great equations was understood that the waves “pick up” the leading to the discovery of radio and Boltz- speed of the current. But Michelson in 1887 mann’s work on the foundations of statistical could find no effect of the passing Aether mechanics, Lord Kelvin’s talk1 at the Royal wind on his very accurate measurements Institution in London on Friday, April 27th of the speed of light, no matter in which 1900, was titled “Nineteenth-century clouds direction he measured it, with headwind or over the dynamical theory of heat and light.” tailwind. -

DISCRETE SPACETIME QUANTUM FIELD THEORY Arxiv:1704.01639V1
DISCRETE SPACETIME QUANTUM FIELD THEORY S. Gudder Department of Mathematics University of Denver Denver, Colorado 80208, U.S.A. [email protected] Abstract This paper begins with a theoretical explanation of why space- time is discrete. The derivation shows that there exists an elementary length which is essentially Planck's length. We then show how the ex- istence of this length affects time dilation in special relativity. We next consider the symmetry group for discrete spacetime. This symmetry group gives a discrete version of the usual Lorentz group. However, it is much simpler and is actually a discrete version of the rotation group. From the form of the symmetry group we deduce a possible explanation for the structure of elementary particle classes. Energy- momentum space is introduced and mass operators are defined. Dis- crete versions of the Klein-Gordon and Dirac equations are derived. The final section concerns discrete quantum field theory. Interaction Hamiltonians and scattering operators are considered. In particular, we study the scalar spin 0 and spin 1 bosons as well as the spin 1=2 fermion cases arXiv:1704.01639v1 [physics.gen-ph] 5 Apr 2017 1 1 Why Is Spacetime Discrete? Discreteness of spacetime would follow from the existence of an elementary length. Such a length, which we call a hodon [2] would be the smallest nonzero measurable length and all measurable lengths would be integer mul- tiplies of a hodon [1, 2]. Applying dimensional analysis, Max Planck discov- ered a fundamental length r G ` = ~ ≈ 1:616 × 10−33cm p c3 that is the only combination of the three universal physical constants ~, G and c with the dimension of length. -

It's About Time Transcript
It’s about time Transcript Date: Thursday, 19 March 2009 - 1:00PM Location: Staple Inn Hall IT'S ABOUT TIME Professor Ian Morison "Time is nature's way of preventing everything happening at once." -John Wheeler Let us first discuss how astronomers measured the passage of time until the 1960's. Local Solar Time For centuries, the time of day was directly linked to the Sun's passage across the sky, with 24 hours being the time between one transit of the Sun across the meridian (the line across the sky from north to south) and that on the following day. This time standard is called 'Local Solar Time' and is the time indicated on a sundial. The time such clocks would show would thus vary across the United Kingdom, as Noon is later in the west. It is surprising the difference this makes. In total, the United Kingdom stretches 9.55 degrees in longitude from Lowestoft in the east to Mangor Beg in County Fermanagh, Northern Ireland in the west. As 15 degrees is equivalent to 1 hour, this is a time difference of just over 38 minutes! Greenwich Mean Time As the railways progressed across the UK, this difference became an embarrassment and so London or 'Greenwich' time was applied across the whole of the UK. A further problem had become apparent as clocks became more accurate: due to the fact that, as the Earth's orbit is elliptical, the length of the day varies slightly. Thus 24 hours, as measured by clocks, was defined to be the average length of the day over one year. -

Can Recurrent Neural Networks Warp Time?
Published as a conference paper at ICLR 2018 CAN RECURRENT NEURAL NETWORKS WARP TIME? Corentin Tallec Yann Ollivier Laboratoire de Recherche en Informatique Facebook Artificial Intelligence Research Université Paris Sud Paris, France Gif-sur-Yvette, 91190, France [email protected] [email protected] ABSTRACT Successful recurrent models such as long short-term memories (LSTMs) and gated recurrent units (GRUs) use ad hoc gating mechanisms. Empirically these models have been found to improve the learning of medium to long term temporal dependencies and to help with vanishing gradient issues. We prove that learnable gates in a recurrent model formally provide quasi- invariance to general time transformations in the input data. We recover part of the LSTM architecture from a simple axiomatic approach. This result leads to a new way of initializing gate biases in LSTMs and GRUs. Ex- perimentally, this new chrono initialization is shown to greatly improve learning of long term dependencies, with minimal implementation effort. Recurrent neural networks (e.g. (Jaeger, 2002)) are a standard machine learning tool to model and represent temporal data; mathematically they amount to learning the parameters of a parameterized dynamical system so that its behavior optimizes some criterion, such as the prediction of the next data in a sequence. Handling long term dependencies in temporal data has been a classical issue in the learning of re- current networks. Indeed, stability of a dynamical system comes at the price of exponential decay of the gradient signals used for learning, a dilemma known as the vanishing gradient problem (Pas- canu et al., 2012; Hochreiter, 1991; Bengio et al., 1994). -

A Geometric Introduction to Spacetime and Special Relativity
A GEOMETRIC INTRODUCTION TO SPACETIME AND SPECIAL RELATIVITY. WILLIAM K. ZIEMER Abstract. A narrative of special relativity meant for graduate students in mathematics or physics. The presentation builds upon the geometry of space- time; not the explicit axioms of Einstein, which are consequences of the geom- etry. 1. Introduction Einstein was deeply intuitive, and used many thought experiments to derive the behavior of relativity. Most introductions to special relativity follow this path; taking the reader down the same road Einstein travelled, using his axioms and modifying Newtonian physics. The problem with this approach is that the reader falls into the same pits that Einstein fell into. There is a large difference in the way Einstein approached relativity in 1905 versus 1912. I will use the 1912 version, a geometric spacetime approach, where the differences between Newtonian physics and relativity are encoded into the geometry of how space and time are modeled. I believe that understanding the differences in the underlying geometries gives a more direct path to understanding relativity. Comparing Newtonian physics with relativity (the physics of Einstein), there is essentially one difference in their basic axioms, but they have far-reaching im- plications in how the theories describe the rules by which the world works. The difference is the treatment of time. The question, \Which is farther away from you: a ball 1 foot away from your hand right now, or a ball that is in your hand 1 minute from now?" has no answer in Newtonian physics, since there is no mechanism for contrasting spatial distance with temporal distance. -
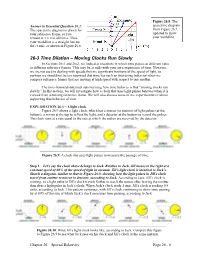
Section 26-3: Time Dilation
Figure 26.8: The Answer to Essential Question 26.2: spacetime diagram The spacetime diagram is drawn for from Figure 26.7, your reference frame, so you updated to show remain at x = 0 at all times. Thus, your worldline. your worldline is a straight line up the ct axis, as shown in Figure 26.8. 26-3 Time Dilation – Moving Clocks Run Slowly In Sections 26-1 and 26-2, we looked at situations in which time passes at different rates in different reference frames. This may be at odds with your own experience of time. However, we are not used to dealing with speeds that are significant fractions of the speed of light, so perhaps we should not be too surprised that time has such an interesting behavior when we compare reference frames that are moving at high speed with respect to one another. The time-honored statement summarizing how time behaves is that “moving clocks run slowly.” In this section, we will investigate how a clock that uses light pulses behaves when it is viewed from a moving reference frame. We will also discuss some of the experimental evidence supporting this behavior of time. EXPLORATION 26.3 – A light clock Figure 26.9 shows a light clock, which has a source (or emitter) of light pulses (at the bottom), a mirror at the top to reflect the light, and a detector at the bottom to record the pulses. The clock runs at a rate equal to the rate at which the pulses are received by the detector. -

How Achilles Could Become an Immortal Hero Every Mother Wants
Albert Einstein changes the world - How Achilles could become an immortal hero Every mother wants their beloved child to stay out of trouble and live a successful life. She cares about her child so much that when something horrible happens to her child, a mother will feel deep sorrow. The same was the case with Thetis, a sea goddess. According to Iliad, her son Achilleus was a great hero with dauntless spirit and high intelligence [1]. Thetis must have been proud of her son’s outstanding talent and amazing skills. However, Achilleus was a mortal, because his father, Peleus, was a human being. Born brave and bold, Achilleus chose to live as a warrior rather than to live long without fame, despite a seer’s prediction that he would die young in the battle against the Trojans. It is unpredictable how deep the goddess’ grief was when he actually died in the Trojan war. In this essay, I would like to show how Einstein’s theory of relativity could be used to make Achilleus immortal. The theory of relativity is a scientific explanation about how space relates to time, which was proposed by physicist, Albert Einstein, in the early 1900s. It revolutionized the concepts of space, time, mass, energy and gravity, giving great impact to the scientific world. In spite of numerous scientific breakthroughs achieved after that, the theory still remains as one of the most significant scientific discovery in human history. The theory of relativity consists of two interrelated theories: special relativity and general relativity. Special relativity is based on two key concepts. -

On Spacetime Coordinates in Special Relativity
On spacetime coordinates in special relativity Nilton Penha * Departamento de Física, Universidade Federal de Minas Gerais, Brazil. Bernhard Rothenstein ** "Politehnica" University of Timisoara, Physics Department, Timisoara, Romania. Starting with two light clocks to derive time dilation expression, as many textbooks do, and then adding a third one, we work on relativistic spacetime coordinates relations for some simple events as emission, reflection and return of light pulses. Besides time dilation, we get, in the following order, Doppler k-factor, addition of velocities, length contraction, Lorentz Transformations and spacetime interval invariance. We also use Minkowski spacetime diagram to show how to interpret some few events in terms of spacetime coordinates in three different inertial frames. I – Introduction Any physical phenomenon happens independently of the reference frame we may be using to describe it. It happens at a spatial position at a certain time. Then to characterize one such event we need to know three spatial coordinates and the time coordinate in a four dimensional spacetime, as we usually refer to the set of all possible events. In such spacetime, an event is a point with coordinates (x,y,z,t) or (x,y,z,ct) as it is much used where c is the light speed in the vacuum, admitted as constant according to the second postulate of special relativity; the first postulate is that “all physics laws are the same in all inertial frames”. Treating the time as ct instead of t has the advantage of improving the transparence of the symmetry that exists between space and time in special relativity. -

Relativity Chap 1.Pdf
Chapter 1 Kinematics, Part 1 Special Relativity, For the Enthusiastic Beginner (Draft version, December 2016) Copyright 2016, David Morin, [email protected] TO THE READER: This book is available as both a paperback and an eBook. I have made the first chapter available on the web, but it is possible (based on past experience) that a pirated version of the complete book will eventually appear on file-sharing sites. In the event that you are reading such a version, I have a request: If you don’t find this book useful (in which case you probably would have returned it, if you had bought it), or if you do find it useful but aren’t able to afford it, then no worries; carry on. However, if you do find it useful and are able to afford the Kindle eBook (priced below $10), then please consider purchasing it (available on Amazon). If you don’t already have the Kindle reading app for your computer, you can download it free from Amazon. I chose to self-publish this book so that I could keep the cost low. The resulting eBook price of around $10, which is very inexpensive for a 250-page physics book, is less than a movie and a bag of popcorn, with the added bonus that the book lasts for more than two hours and has zero calories (if used properly!). – David Morin Special relativity is an extremely counterintuitive subject, and in this chapter we will see how its bizarre features come about. We will build up the theory from scratch, starting with the postulates of relativity, of which there are only two.