DOCSLIB.ORG

ROCK STRENGTH (Text Ch. 3)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ROCK STRENGTH (Text Ch. 3) Lecture 9 – Introduction to Rock Strength David Hart University of Wisconsin ecow.engr.wisc.edu/cgi- bin/get/gle/474/hartdavid/notes/lectu re9strengthintro.ppt - ROCK STRENGTH • Shear fracture is the dominant mode of failure for rocks under all but the lowest confining stress. Extension Compression Paterson, Experimental Rock Deformation – The Brittle Field Example from Goodman, Intro to Rock Mechanics ROCK STRENGTH • The peak stress is the strength of the rock. – It may fail catastrophically if the load frame is “soft”. Example below is for a “stiff” frame. • The compressive strength of rock is a function of the confining pressure. • As the confining pressure increases so does the strength. Goodman, Intro to Rock Mechanics ROCK STRENGTH • The variation of peak stress σ1, peak (at which failure occurs) with the confining pressure (for which σ2 = σ3 ) is referred to as the rock CRITERION OF FAILURE. • The simplest and the best known failure criterion of failure is the MOHR-COULOMB (M-C) criterion: the linear approximation of the variation of peak stress σ1, peak with the confining pressure. MOHR-COULOMB Criterion of Failure • It has been established that rock fails in σ1,p compression by shearing along a ‘failure’ plane oriented at an angle θ with respect to σ1 that is specific for a particular rock. Rock • The M-C linear strength criterion cylinder σ =σ implies that θ stays the same regardless 2 3 of the confining pressure applied. τ 2θ 2θ 2θ σ 0 σ2=σ3 1,p σ MOHR-COULOMB Criterion τ = Si + σ tanφ τ cr φ A D 2θ Sι φ 90o C 0 σ2=σ3 Co B σ1,p σ MOHR-COULOMB Criterion in terms of shear and normal stress on the plane of failure τ cr = Si + σ tanφ where Iτlcr is the shear strength, Si (cohesion) is the intercept with the τ axis of the linear envelope, and φ ('angle of friction') is the slope angle of the linear envelope of failure. The relationship between the angle θ (the angle between the normal to the plane of failure -point A- and the direction of the max. principal stress) and φ is π φ =2θ + φ or θ =o 45 + 2 2 MOHR-COULOMB Criterion can also be given The Mohr-Coulomb criterion do this we oin terms of the principal stresses. T recall the following relationships: σ −σ σ +σ σ −σ τ = 1 2sin 2θ σ =1 2+ 1cos 2 2θ 2 2 2 Plug these relationships into the Mohr-Coulomb criterion: τ crS= i +σ tanφ and you get: σ1, p−σ 2 1⎛σ, p+σ 2σ, 1 p−σ 2 ⎞ sin2θ=i S +⎜ + cosθ2 ⎟ tan φ 2 ⎝ 2 2 ⎠ MOHR-COULOMB Criterion in Terms of Principal Stresses By separating all the terms containing σ1 from the rest of the expression, and recalling the above relationship between θ and φ (and also performing some trigonometric manipulations), we finally obtain the Mohr- Coulomb criterion in terms of the principal stresses only: ⎛ φ ⎞ 2⎛ φ ⎞ σ,1 p2=S i tan⎜ ° 45 + ⎟ +σ 2 tan ⎜45° + ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ or: 2⎛ φ ⎞ 1σ,= pC 0 +σ 2 tan⎜45° + ⎟ ⎝ 2 ⎠ MOHR-COULOMB Criterion in Terms of Principal Stresses ⎛ φ ⎞ 2⎛ φ ⎞ σ,1 p2=S i tan⎜ ° 45 + ⎟ +σ 2 tan ⎜45° + ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ or: 2⎛ φ ⎞ σ 1σ,= pC 0 +σ 2 tan⎜45° + ⎟ 1 ⎝ 2 2⎛ o φ⎞ ⎠ tan⎜ 45+ ⎟ ⎝ 2⎠ Remember: the angle 1 45+φ/2 is equal to θ, where θ is the angle ⎛ o φ⎞ C 2o = Si tan⎜ + ⎟ 45 between the direction ⎝ 2⎠ 0 of σ1 and the normal σ2= σ 3 to the plane of failure. Example The criterion of failure of a limestone is given by (in MPa): τ = 10 + 0.8σ cr Represent the same criterion in terms of principal stresses. Solution From the given equation we deduce that: Si = 10 MPa, and tan φ = 0.8, or φ = 38.7 °. The criterion of failure in terms of principal stresses is: ⎛ φ ⎞ 2⎛ φ ⎞ σ,1 p2=S i tan⎜ ° 45 + ⎟ +σ 2 tan ⎜45° + ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ By plugging the given values in the above equation we obtain (in MPa): ⎛ 38. ° 7⎞ 2⎛ 38. ° 7⎞ σ=,12 p × 10tan⎜ 45 ° + ⎟ +σ 2 tan ⎜45° + ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ EXAMPLES OF MOHR- τ COULOMB CRITERION: 1. Hydrostatic state of stress: O P σ σ1 = σ2 = σ3 = P When does rock fail under this condition? 2. Uniaxial compression: τ σ1 ≠ 0 ; σ2 = σ3 = 0 φ D Failure occurs when σ1 A attains its peak value C . o S Failure plane (point A) i φ normal is at θ=(45 + φ/2) to =C σ1 direction. O B σ1,p o σ MOHR-COULOMB Criterion- Tensile Stresses Question: What if the normal stress on the plane of failure is tensile? This implies that there is no contact between the two created surfaces and hence there is no frictional resistance. Thus, the Mohr-Coulomb (M-C) criterion loses its validity. Note, however, that σ2 can be tensile as long as the normal stress σ remains compressive: Mohr- Coulomb criterion will still be valid. Remember that σ2=σ3 can never be less than the tensile strength of the rock T, since T implies tensile failure. MOHR-COULOMB Criterion- Tensile Stresses Case I: σ2 and σ are both tensile, so M-C criterion does not apply. Specimen fails in tension when σ2 = T. Case II: σ2 is tensile, but σ is zero or larger, so M-C criterion DOES apply! Case III: All stresses are compressive so M-C does apply. NOTE: Typically T = 0.1Co to 0.05Co MOHR-COULOMB CRITERION IN TERMS OF THE PRINCIPAL STRESS RATIO K Engineers/practitioners like to to work with principal stress ratio K = σ2 / σ1 (typically σ2 represents the horizontal stress σh, and σ1 represents the vertical stress σv ). It is thus more convenient on occasion to express the Mohr-C criterion in terms of K. MOHR-COULOMB CRITERION IN TERMS OF THE PRINCIPAL STRESS RATIO K Given: 2 φ σ1,p = Co + σ2 tan (45° + ) 2 We divide both sides by σ1,p: 2 φ 1 = Co + σ2 tan (45° + ) σ1,p σ1,p 2 Using K and rearranging terms, we obtain: Co 2 φ Co = 1 - K tan (45° + ) σ1,p = σ1,p 2 φ 1 - K tan2 (45° + ) 2 MOHR-COULOMB CRITERION IN TERMS OF THE PRINCIPAL STRESS RATIO K With the M-C criterion written this way we can determine a limit for the ratio K at failure. It is 2 φ K < cot (45° + ) 2 This condition makes the criterion feasible. Otherwise the failure stress is infinite or negative, which is not physically possible. MOHR-COULOMB CRITERION IN TERMS OF THE PRINCIPAL STRESS RATIO K This condition for K is a useful tool in determining stability. For example if the angle φ = 40° then K < 0.22 Or σ2 < 0.22 σ1 . CLASS: What if the angle φ = 0°? Determining the Critical State of Stress at a Point in a Rock Formation When the M-C Criterion of Failure and One of the Principal Stresses Are Known In this example the φ an strength material τ σt i + S properties of the rock = τ cr Si and φ are given, Given and we also know the σ at failure. σ 1,p σ What is then the 1,p complete state of stress at the point in question? φ Let’s imagine τ first that we have solved the A problem, i.e. we R have found the C B R σ σ2 σ1,p CRITICAL Mohr 90 + φ circle denoting the state of 180 − (90 + φ) = 45 − φ / 2 stress at failure. 2 We notice that in the triangle ABC two of the sides are equal to the radius R. Also, recall φ the value of the angle τ ABC. Hence the angle A ACB is 45° - φ/2. R Thus, in order to C B R σ σ2 σ1,p construct the critical 90 + φ Mohr circle we fist plot 180 − (90 + φ) the M-C criterion and = 45 − φ / 2 2 the point representing σ1,p. Then, we construct the angle ACB and φ draw the line CA, τ where A intersects A the M-C criterion. Now we construct IIa II I D C σ an identical angle B σ2 σ1,p CAB and draw AB. (90 +φ) Point B on the σ 180 − (90 + φ) = 45 − φ / 2 axis is the center 2 of the critical Mohr circle. An alternate way is to construct at point A a 90° angle and draw line AD. Point D has to be equal to σ2. OTHER EMPIRICAL MOHR ENVELOPES Goodman, Intro to Rock Mechanics A straight line doesn’t always fit the data well Mohr-Coulomb is an approximation OTHER EMPIRICAL MOHR ENVELOPES Several examples of other expressions defining the Mohr envelope in rocks for which the Coulomb linear relationship does not appear to be representative, can be found in the literature. These are all EMPIRICAL relationships. The Hoek and Brown criterion is particularly popular now: σ σ σ 1,p = 2 + m 2 + s C o Co Co where m and s are constants of the material and are determined empirically. SIZE EFFECT ON COMPRESSIVE STRENGTH It has been found through experimentation that rock strength is affected by the SIZE of the specimen tested. This can be explained simply as being the result of the many flaws found in rock in the form of fissures, pores, cleavage, bedding planes, foliation, etc. The larger the size of the specimen tested the higher the probability that a weak flaw will be available, capable of initiating failure.
Load more

Recommended publications
  • Compressive Behavior Characteristics of High-Performance Slurry-Infiltrated Fiber-Reinforced Cementitious Composites (Sifrccs) Under Uniaxial Compressive Stress
    materials Article Compressive Behavior Characteristics of High-Performance Slurry-Infiltrated Fiber-Reinforced Cementitious Composites (SIFRCCs) under Uniaxial Compressive Stress Seungwon Kim 1 , Seungyeon Han 2, Cheolwoo Park 1,* and Kyong-Ku Yun 2,* 1 Department of Civil Engineering, Kangwon National University, 346 Jungang-ro, Samcheok 25913, Korea; [email protected] 2 KIIT (Kangwon Institute of Inclusive Technology), Kangwon National University, 1 Gangwondaegil, Chuncheon 24341, Korea; [email protected] * Correspondence: [email protected] (C.P.); [email protected] (K.-K.Y.); Tel.: +82-33-570-6515 (C.P.); +82-33-250-6236 (K.-K.Y.) Received: 11 October 2019; Accepted: 19 December 2019; Published: 1 January 2020 Abstract: The compressive stress of concrete is used as a design variable for reinforced concrete structures in design standards. However, as the performance-based design is being used with increasing varieties and strengths of concrete and reinforcement bars, mechanical properties other than the compressive stress of concrete are sometimes used as major design variables. In particular, the evaluation of the mechanical properties of concrete is crucial when using fiber-reinforced concrete. Studies of high volume fractions in established compressive behavior prediction equations are insufficient compared to studies of conventional fiber-reinforced concrete. Furthermore, existing prediction equations for the mechanical properties of high-performance fiber-reinforced cementitious composite and high-strength concrete have limitations in terms of the strength and characteristics of contained fibers (diameter, length, volume fraction) even though the stress-strain relationship is determined by these factors. Therefore, this study developed a high-performance slurry-infiltrated fiber-reinforced cementitious composite that could prevent the fiber ball phenomenon, a disadvantage of conventional fiber-reinforced concrete, and maximize the fiber volume fraction.
    [Show full text]
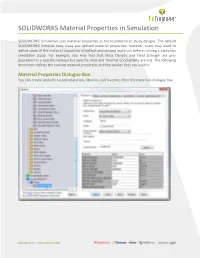
  • SOLIDWORKS Material Properties in Simulation
    SOLIDWORKS Material Properties in Simulation SOLIDWORKS Simulation uses material properties as the foundation to study designs. The default SOLIDWORKS material have many pre-defined material properties; however, users may need to define some of the material properties of default and custom materials before running a particular simulation study. For example, you may find that Mass Density and Yield Strength are pre- populated in a specific material but Specific Heat and Thermal Conductivity are not. The following document defines the custom material properties and the studies they are used in. Material Properties Dialogue Box You can create and edit custom materials, libraries and favorites from the materials dialogue box. 888.688.3234 | GOENGINEER.COM Elastic Modulus The Elastic Modulus (Young’s Modulus) is the ratio of stress versus strain in the X, Y or Z directions. Elastic Moduli are used in static, nonlinear, frequency, dynamic, and buckling analyses. Poisson's Ratio Poisson’s Ratio is the negative ratio between transverse and axial strain. Poisson’s ratios are dimensionless quantities. For isotropic materials, the Poisson’s ratios in all planes are equal. Poisson ratios are used in static, nonlinear, frequency, dynamic and buckling Shear Modulus Shear Modulus (Modulus of Rigidity) is the ratio of shear stress to shear strain Shear Moduli are used in static, nonlinear, frequency, dynamic and buckling analyses. Mass Density Mass Density is used in static, nonlinear, frequency, dynamic, buckling, and thermal analyses. Static and buckling analyses use this property only if you define body forces (gravity and/or centrifugal). Tensile Strength Tensile Strength is the maximum that a material can withstand before stretching or breaking.
    [Show full text]
  • The Strength of Concrete
    The Strength of Chapter Concrete 3 3.1 The Importance of Strength 3.2 Strength Level Required KINDS OF STRENGTH 3.3 Compressive Strength 3.4 Flexural Strength 3.5 Tensile Strength 3.6 Shear, Torsion and Combined Stresses 3.7 Relationship of Test Strength to the Structure MEASUREMENT OF STRENGTH 3.8 Job-Molded Specimens 3.9 Te s t i n g o f H a r d e n e d C o n c r e t e FACTORS AFFECTING STRENGTH 3.10 General Comments 3.11 Causes of Strength Variations –Cement – Aggregates – Mix Proportioning – Making and Handling the Concrete – Temperature and Curing 3.12 Apparent Low Strength 3.13 Accelerated Strength Development – High-Early-Strength Cement –Admixtures – Retention of Heat of Hydration – High-Temperature Curing – Rapid-Setting Cements 3.14 Slow Strength Development HIGH-STRENGTH CONCRETE (HSC) 3.15 Selection of Materials and Mix 3.16 Handling and Quality Control EARLY MEASUREMENT OF STRENGTH EXPOSURE TO HIGH TEMPERATURE 3.17 Long-Time Exposure 3.18 Fire-Damaged Concrete 3 The Strength of Concrete The quality of concrete is judged largely on the strength of that concrete. Equipment and methods are continually being modernized, testing methods are improved, and means of analyzing and interpreting test data are becoming more sophisticated. Prior to the 2008 edition of the ACI 318 Standard, we relied almost exclusively on the strength of 6-by-12-inch cylinders, made on the jobsite and tested in compression at 28 days age for evaluation and acceptance of concrete. The use of 4-by-8-inch cylinders for strength evaluation was first addressed in ACI 318-08.
    [Show full text]
  • Comparison of Tensile and Compressive Properties of Carbon/Glass Interlayer and Intralayer Hybrid Composites
    materials Article Comparison of Tensile and Compressive Properties of Carbon/Glass Interlayer and Intralayer Hybrid Composites Weili Wu 1 ID , Qingtao Wang 1 ID and Wei Li 1,2,3,* ID 1 College of Textiles, Donghua University, No. 2999, Northern Renmin Rd., Songjiang District, Shanghai 201620, China; [email protected] (W.W.); [email protected] (Q.W.) 2 Key Lab of Textile Science & Technology, Ministry of Education, Shanghai 201620, China 3 Center for Civil Aviation Composites, Shanghai 201620, China * Correspondence: [email protected]; Tel.: +86-137-6402-2421 Received: 27 May 2018; Accepted: 25 June 2018; Published: 28 June 2018 Abstract: Tensile and compressive properties of interlayer and intralayer hybrid composites were investigated in this paper. The tensile modulus and compression modulus of interlayer and intralayer hybrid composites are the same under the same mixed ratio, the tensile strength is much superior to the compression strength, and while the tensile modulus and strength increase along with the carbon fiber content, the compression values change slightly. The influence of stacking structures on the tensile and compressive strengths is opposite to the ratio of T/C (tensile/compression) strength for interlayer hybrid composites, and while the tensile and compression strengths with glass fiber sandwiching carbon fiber can reach the maximum value, the ratio of T/C strength is minimum. For structures with carbon fiber sandwiching glass fiber, or with asymmetric structures, the tensile and compressive strengths are at a low value. For intralayer hybrid structures, while the carbon/glass (C/G) dispersion degree is high, the tensile and compression strengths are low.
    [Show full text]
  • The Mechanical Properties of Saline Ice Under Uniaxial Compression Gary A
    IGS lntern•tional Symp<>Sium Ofl Applied (a! and Snow Re:sevd!:, Rovaniemi. Flnland; 18·23 April 1993 The Mechanical Properties of Saline Ice Under Uniaxial Compression Gary A. Kuehn and Briand M. Schulson Ice Research Laboratory Thayer School of Engineering, Dartmouth College 8000 Cummings Hall, Hanover, NH 03755-8000 603-646-3763, 603-646-3828 : FAX [email protected] : internet [email protected] : internet Annals of Glaciology ABSTRACT (in press, June 1993) Understanding the mechanical properties of saline ice is important for engineering design as well as for operations in polar regions. In order to gain understanding of the basic mechanisms of deformation and fracture, laboratory-grown columnar saline ice, representative of first-year sea ice, was tested in uniaxial comptession under a variety of conditions of strain rate oo-7 to 10-1 per second), temperature (-40', -20', -10· and .5·c) and orientation (loading vertically or horizontally: i.e. parallel or perpendicular to the growth direction). The range of strain rate spanned the ductile-to-brittle transition for every combination of temperature and specimen orientation. The results of over 250 tests are reported. Mechanical properties, failure mode and ice structure are analyzed with respect to the testing conditions. The results show that strength is dependent upon the ice structure, orientation, strain rate and temperature. During loading in the ductile regime the structure is altered (e.g. by recrystallization), whereas in the brittle regime the majority of the structural change is through cracking. The results are compared to results from the literature on both natural sea ice and laboratory-grown saline ice.
    [Show full text]
  • A New Expansion Material Used for Roof-Contacted Filling Based on Smelting Slag
    www.nature.com/scientificreports OPEN A new expansion material used for roof‑contacted flling based on smelting slag Hua Na1, Guocheng Lv1*, Lijuan Wang1, Libing Liao1, Dan Zhang2, Lijie Guo2* & Wenchen Li2 The improper handling of smelting slag will seriously pollute the environment, and the unflled roof of the goaf of the mine will threaten the safety of the mine. Expansion materials have attracted more and more attention because of their excellent properties. In this paper, copper‑nickel smelting slag that has some active ingredients of gelling is used instead of traditional aggregate and some part of cement in order to reduce its pollution to the environment and its costs. For safety reasons, hydrogen peroxide was chosen as the foaming agent. Sodium silicate and hexadecyl trimethyl ammonium bromide (CTAB) are used as additives. Our results showed that after 28 days of curing, the material has better mechanical properties and the early compressive strength of the material was enhanced by sodium silicate. The efciency of foaming was improved by CTAB. It also proves that copper–nickel smelting slag can be used in expansion material. At the same time, the utilization rate of the copper– nickel smelting slag of this formula can reach 70%, reduce its pollution to the environment. Mineral resources are one of the most critical parts of the development of society. Filling mining technology is a mining technology that uses flling materials to fll underground goaf. Tere are many kinds of flling materi- als, such as barren rocks, slags, tailings, cementitious material and cementitious material prepared with cement and the solid waste mentioned above in the land mines 1–8.
    [Show full text]
  • Glossary of Transportation Construction Quality Assurance Terms
    TRANSPORTATION RESEARCH Number E-C235 August 2018 Glossary of Transportation Construction Quality Assurance Terms Seventh Edition TRANSPORTATION RESEARCH BOARD 2018 EXECUTIVE COMMITTEE OFFICERS Chair: Katherine F. Turnbull, Executive Associate Director and Research Scientist, Texas A&M Transportation Institute, College Station Vice Chair: Victoria A. Arroyo, Executive Director, Georgetown Climate Center; Assistant Dean, Centers and Institutes; and Professor and Director, Environmental Law Program, Georgetown University Law Center, Washington, D.C. Division Chair for NRC Oversight: Susan Hanson, Distinguished University Professor Emerita, School of Geography, Clark University, Worcester, Massachusetts Executive Director: Neil J. Pedersen, Transportation Research Board TRANSPORTATION RESEARCH BOARD 2017–2018 TECHNICAL ACTIVITIES COUNCIL Chair: Hyun-A C. Park, President, Spy Pond Partners, LLC, Arlington, Massachusetts Technical Activities Director: Ann M. Brach, Transportation Research Board David Ballard, Senior Economist, Gellman Research Associates, Inc., Jenkintown, Pennsylvania, Aviation Group Chair Coco Briseno, Deputy Director, Planning and Modal Programs, California Department of Transportation, Sacramento, State DOT Representative Anne Goodchild, Associate Professor, University of Washington, Seattle, Freight Systems Group Chair George Grimes, CEO Advisor, Patriot Rail Company, Denver, Colorado, Rail Group Chair David Harkey, Director, Highway Safety Research Center, University of North Carolina, Chapel Hill, Safety and Systems
    [Show full text]
  • Concrete Terminology
    DIVISION 3 - CAST IN PLACE CONCRETE TERMINOLOGY A. CONCRETE: A mixture of 1 part Portland Cement ( 22 lbs ) 2 Parts Dry Sand ( 41 lbs ) 3 Parts Dry Aggregate ( 70 lbs ) ½ Part Water ( 10 lbs ) Admixtures ( 7 lbs ) Total Weight Per Cu. Foot = 150 lbs. Area of 1 CU. FT. 1,728 cu. Inches 1. CAST IN PLACE CONCRETE: Concrete that is formed, poured and cured in it’s permanent position. 2. CURED CONCRETE: Concrete which has reached dehydration and obtained it’s maximum compressive strength. 3. GREEN CONCRETE: Concrete which remains hydrated and is in it’s earliest setting stage and has not hardened or cured appreciably. 4. LIGHTWEIGHT CONCRETE: A concrete mixture of substantially lower unit weight and compressive strength than that made from crushed stone or rock aggregate. Typically used on upper floors or roof tops where normal compressive strength is not a requirement and weight is a factor. 5. MONOLITHILIC CONCRETE: A single pour which includes the footing and slab concrete in a single pour . 6. POST-TENSION CONCRETE: A method of stressing reinforced concrete by which the tendons or cables are tightened after the concrete slab has hardened and in place. 24 7. PRE-CAST CONCRETE: Concrete which is cast and cured in a place other than it’s final resting position. ( Beams, Columns, Slabs, Lintels ) 8. PRE-STRESSED CONCRETE: A process of preparing concrete slabs and beams for extra strength by pouring concrete over tightly drawn steel cables, steel rods or tendons. 9. REINFORCED CONCRETE: Concrete with added materials such as steel rod, wire mesh, fiber mesh, dowel bars, expanded metal fabric, or cold drawn wire cable which act together with the concrete to resist cracking or movement B.
    [Show full text]
  • Reinforced Concrete Design
    FALL 2013 C C Reinforced Concrete Design CIVL 4135 • ii 1 Chapter 1. Introduction 1.1. Reading Assignment Chapter 1 Sections 1.1 through 1.8 of text. 1.2. Introduction In the design and analysis of reinforced concrete members, you are presented with a problem unfamiliar to most of you: “The mechanics of members consisting of two materials.” To compound this problem, one of the materials (concrete) behaves differently in tension than in compression, and may be considered to be either elastic or inelastic, if it is not neglected entirely. Although we will encounter some peculiar aspects of behavior of concrete members, we will usually be close to a solution for most problems if we can apply the following three basic ideas: • Geometry of deformation of sections will be consistent under given types of loading; i.e., moment will always cause strain to vary linearly with distance from neutral axis, etc. • Mechanics of materials will allow us to relate stresses to strains. • Sections will be in equilibrium: external moments will be resisted by internal moment, external axial load will be equal to the sum of internal axial forces. (Many new engineers overly impressed speed and apparent accuracy of modern structural analysis computational procedures think less about equilibrium and details). We will use some or all of these ideas in solving most of the analysis problems we will have in this course. Design of members and structures of reinforced concrete is a problem distinct from but closely related to analysis. Strictly speaking, it is almost impossible to exactly analyze a concrete structure, and to design exactly is no less difficult.
    [Show full text]
  • Mechanical Properties of Concrete and Steel Reinforced Concrete (RC
    Mechanical Properties of Concrete and Steel Reinforced Concrete (RC, also called RCC for Reinforced Cement Concrete) is a widely used construction material in many parts the world. Due to the ready availability of its constituent materials, the strength and economy it provides and the flexibility of its forms, RC is often preferred to steel, masonry or timber in building structures. From a structural analysis and design point of view, RC is a complex composite material. It provides a unique coupling of two materials (concrete, steel) with entirely different mechanical properties. Stress-Strain Curve for Concrete Concrete is much stronger in compression than in tension (tensile strength is of the order of one-tenth of compressive strength). While its tensile stress-strain relationship is almost linear [Fig. 1.1(i)], the stress () vs. strain () relationship in compression is nonlinear. Fig. 1.1(ii) shows a typical set of such curves. These curves are different for various ultimate strengths of concrete, particularly the peak stress and ultimate strain. They consist of an Stress initial relatively elastic portion in Stress f w hich stress and strain are closely c proportional, then begin to curve to the horizontal, reaching maximum stress, i.e., the compressive strength f , at a strain of approximately 0.002, c and finally show a descending branch. They also show that concrete Strain, 0.002 Strain, of lower strength are more ductile; Fig. 1.1: - curves of Concrete in (i) tension, (ii) compression i.e., fail at higher strains. The tensile strength as well as the modulus of elasticity of concrete are both proportional to the square-root of its ultimate strength, fc, and can be approximated by ft = 6 fc…………(1.1), Ec = 57500 fc…………(1.2) [in psi].
    [Show full text]
  • Study on Strength, Deformation Characteristics and Interaction
    985 A publication of CHEMICAL ENGINEERING TRANSACTIONS VOL. 59, 2017 The Italian Association of Chemical Engineering Online at www.aidic.it/cet Guest Editors: Zhuo Yang, Junjie Ba, Jing Pan Copyright © 2017, AIDIC Servizi S.r.l. ISBN 978-88-95608- 49-5; ISSN 2283-9216 DOI: 10.3303/CET1759165 Study on Strength, Deformation Characteristics and Interaction between Soil and Stone of Soil-Rock Mixture Yuxu Zhang Hubei Polytechnic University, Huangshi 435003, China [email protected] Soil and rock mixture is a kind of non-uniform, discontinuous, internal structure of complex and irregular geological body. Unlike the general soil, it is a multiphase system. The mechanical properties of the various components constituting the soil-rock mixture are very different. At the same time there is a complex interaction between soil and stone. In this paper, we study the strength and deformation characteristics of soil- rock mixture and the interaction of soil and rock. With the increase of confining pressure, the shear strength of the soil-rock mixture is increased. The amount of displacement of the upper breccias is the largest. The displacement of the central breccias is small and produces both lateral and vertical displacements. The lower breccias produce almost no vertical displacement, but the outside breccias produced a significant lateral displacement. The breccias will rotate during the cutting of soil samples. And the angle of rotation is related to the size, shape, direction, spatial position, force state, and the interaction between the breccias. The breccias will be subjected to different tensile stresses by the soil during the shearing process.
    [Show full text]
  • Design of Compression Members
    CE 405: Design of Steel Structures – Prof. Dr. A. Varma CHAPTER 3. COMPRESSION MEMBER DESIGN 3.1 INTRODUCTORY CONCEPTS • Compression Members: Structural elements that are subjected to axial compressive forces only are called columns. Columns are subjected to axial loads thru the centroid. • Stress: The stress in the column cross-section can be calculated as P f = (2.1) A where, f is assumed to be uniform over the entire cross-section. • This ideal state is never reached. The stress-state will be non-uniform due to: - Accidental eccentricity of loading with respect to the centroid - Member out-of –straightness (crookedness), or - Residual stresses in the member cross-section due to fabrication processes. • Accidental eccentricity and member out-of-straightness can cause bending moments in the member. However, these are secondary and are usually ignored. • Bending moments cannot be neglected if they are acting on the member. Members with axial compression and bending moment are called beam-columns. 3.2 COLUMN BUCKLING • Consider a long slender compression member. If an axial load P is applied and increased slowly, it will ultimately reach a value Pcr that will cause buckling of the column. Pcr is called the critical buckling load of the column. 1 CE 405: Design of Steel Structures – Prof. Dr. A. Varma P (a) Pcr (b) What is buckling? Buckling occurs when a straight column subjected to axial compression suddenly undergoes bending as shown in the Figure 1(b). Buckling is identified as a failure limit-state for columns. P P cr Figure 1. Buckling of axially loaded compression members • The critical buckling load Pcr for columns is theoretically given by Equation (3.1) π2 E I Pcr = (3.1) ()K L 2 where, I = moment of inertia about axis of buckling K = effective length factor based on end boundary conditions • Effective length factors are given on page 16.1-189 of the AISC manual.
    [Show full text]