DOCSLIB.ORG

Computational Photography Filtering: Smoothing Objectives Example

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computational Photography Filtering: Smoothing Objectives Example Filtering: Smoothing • Point-process and Neighboring Pixels Computations on an Image for Image Smoothing Computational Photography CS 4475/6475 Maria Hybinette 1 Maria Hybinette 2 Maria Hybinette Objectives From Pixel/Point Operations to Groups of Pixels • Smooth an image while considering a neighborhood n of pixels – Average filtering (use the average of n) – Median filtering (use the median of n) • special non-linear filtering and smoothing • Previously we used pixel to pixel arithmetic (e.g., add(), sub())) approach • How to Smooth a Signal? • Approach: Use a group of pixels : Neighboring Values of a neighborhood. 1. Moving Average [1 1 1 1 1] X 1/5 2. Weighted Moving Average [1 4 6 4 1] X 1/16 3 Maria Hybinette 4 Maria Hybinette Example: 3x3 Kernel Example: 3x3 Kernel • Smoothing Process over an Image using Averages • 1*90/9=10, 2*90/9=20, …. 5 Maria Hybinette 6 Maria Hybinette Results in Shades of Gray • What about the edges? 7 Maria Hybinette 8 Maria Hybinette Edges Mathematical Notation, Observations, and Computing the Result Matrix • A Small image ‘h’ is “rubbed” over (larger) image ‘F’ that we are smoothing • Kernel: h – Example: 3x3 area around each original pixel used – Neighborhood size – k=1, window size = 3. – k >1, • Window size is 2k+1 – k=1, 2(1)+1 = 3 – Our kernel is 3x3 – Recall : A pixel is referenced by (i, j) • Expand the image we are smoothing: • Want Result Matrix ‘G’ – Wrap around pixels. (3x3 filter needs one more pixel – F à G using h. on each border, 5x5 needs 2) – G = h (operation) F – 9 Copy edges Maria Hybinette 10 Maria Hybinette Computing the Values ofA Result Mathematical Matrix RepresentationSmoothing when for a- iSmoothing are all 1s. Observations (continued)1 G[3, 3] = (A + B + C + D + E + FG[3, 3] = 1/9 (A + B + C + D + E + F + G + H + I ) + G + H + I) a b c 20 20 10 20 10 20 10 10 13 9 30 0 0 0 0 0 0 0 30 1 k k d e f k k G[i, j] = F[i + u, j + v] Let’s refer to F[i,j] as input and 1 2 ∑ ∑ 20 0 90A 90B 90C 90 90 0 20 20 20 10 20 10 20 10 10 13(2k +1) u k v k • Let’s refer to G[i, j]= F [i + u, j + v] =− =− g h i 20 0 90 0 90 90 90 0 20 2 30 0 0 0 0 0 0 0 30 20 0 D E F 90 90 0 20 G[i,j] as output, h[i,j] as the kernel(2k + 1) 1 – F[i,j] as input and u= k v=20 0k 90A 90B 90C 90 90 0 20 10 0 90 90 90 90 90 0 10 X− X− • ( 2 k + 1 ) 2 “Standardizes” the weight to 10 0 G H I 90 90 0 10 – G[i,j] as output 20 0 90D E0 90F 90 90 0 20 10 0 90 90 90 90 90 0 10 a b c A B C 10 0 90G 90H 90I 90 each90 0 10 pixel . (k=1, then 1/9) 10 0 90 90 90 90 90 0 10 G[3, 3] = a A + b B + c C + d D 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 k90 k 0 10 10 0 90 90 90 90 90 0 10 – h[i,j] as the kernel⇤ ⇤ ⇤ ⇤ d e f D E F F[i u, j v] + e E + f F + h H + i I A 10Mathematical0 90 90 90•90 ∑ 90 ∑ 0 10 + + Loop over allRepresentation pixels in 20 0 0 0 0 0 0 for0 20 Smoothing u=−k v=−k 20 0 0 0 0 0 0 0 20 • Example: pixel⇤ (3,3) ⇤(expanded⇤ edges⇤ above)g h i G H I 20 0 0 0 0 0 neighborhood0 0 20 around particular 20 20 10 20 10 20 10 10 13 20 20 10 20 10 20 10 10 13 20 20 10 20 10 20 10 10 13 – G[3, 3] = a*A + b*B + c*C + d*D +e*E + f*F + h*H + i*I 1 image pixel F[i,j] Attribute uniform1/9 1/9 1/9 Loop over all pixels in a b c 20 20 10 20 10 20 10 10 13 1 G[3, 3] = (A +– Bstarting+ C from+ upperD + rightE corner,+ F -k,+ -k,G if+ H + I) 1/9 1/9 1/9 9 G[3, 3] = (A + B + C + D + E + F + G + H + I) k=1, then 1 left, from center and up 1. 30 0 0 0 0 0 0 0 30 9 k k d e f – If all weights (a through i) are 1: weight to1/9 each1/9 1/9 neighborhood1 around 20 0 90A 90B 90C 90 90 0 20 G[i, j]= F [i + u, j + v] g h i 11 – G[3, 3] = 1/9 (A + B + C + D + E + F + G + H + I ) Maria Hybinette (2k 12+ 1)2 Maria Hybinette 20 0 90D 0E 90F 90 90 0 20 © 2015 Irfan Essa, Georgia Tech, All Rights Reserved pixel imageu= k v =pixelk F[i,j] 10 0 90 90 90 90 90 0 10 X− X− 10 0 G H I 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 20 0 0 0 0 0 0 0 20 20 0 0 0 0 0 0 0 20 © 2015 Irfan Essa, Georgia Tech, All Rights Reserved 20 20 10 20 10 20 10 10 13 Attribute uniform Loop over all pixels in20 20 10 20 10 20 10 10 13 weight to each neighborhood around pixel image pixel F[i,j] © 2015 Irfan Essa, Georgia Tech, All Rights Reserved A Mathematical RepresentationGeneralize the foruniform Smoothing weight Example: Box Filter for Smoothing 1 G[3, 3] = (A + B + C + D + E +G[3, 3] = 1/9 (A + B + C + D + E + F + G + H + I ) F + G + H + I) a b c 20 20 10 20 10 20 10 10 13 9 k k 30 0 0 0 0 0 0 0 30 k k 1 d e f G[i, j] = F[i + u, j + v] 20 0 90A 90B 90C 90 90 0 20 1 (2k +1)2 ∑ ∑ G[i, j]= F [i + u, j + v] u=−k v=−k g h i (2k + 1)2 20 0 90D 0E 90F 90 90 0 20 u= k v= k 10 0 90 90 90 90 90 0 10 X− X− • More Generally, 10 0 G H I 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 G[i, j] = a * A + b* B + c*C + d * D + e* E + f * F + h * H +i* I 20 0 0 0 0 0 0 0 20 A Mathematical Representation20 0 0 0 0 0 0 0for20 Smoothing k k 20 20 10 20 10 20 10 10 13 G[i, j] = ∑ ∑ h[u, v]* F[i + u, j + v] 20 20 10 20 10 20 10 10 13 1 u=−k v=−k • Uniform Kernel (all 1s). Attribute uniformG[3, 3] = Loop( A + B over+ C + Dall+ E +pixelsF + G + inH + I) a b c 20 20 10 20 10 20 10– Box10 Area13 above is 21x21 the larger the kernel the ‘smoother’ the 9 result. • Formula is Referred to Cross 30 0 0 0 0 0 0 0 30 k k d e f • The larger the box the smoother it gets. weight to each neighborhood1Correlation more onaround this later. 20 0 90A 90B 90C 90 90 0 20 G[i, j]= F [i + u, j + v] g h i (2k 13+ 1)2 Maria Hybinette 20 0 90D 0E 90F14 90 h7ps://90 0 en.wikipedia.org20 /wiki/Box_blur Maria Hybinette pixel imageu= k v =pixelk F[i,j] 10 0 90 90 90 90 90 0 10 X− X− 10 0 G H I 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 10 0 90 90 90 90 90 0 10 20 0 0 0 0 0 0 0 20 20 0 0 0 0 0 0 0 20 © 2015 Irfan Essa, Georgia Tech, All Rights Reserved 20 20 10 20 10 20 10 10 13 20 20 10 20 10 20 10 10 13 SpecialSpecialAttribute Case:Case: uniform MedianMedian Loop over Filtering all pixels in Specialweight Example:to eachCase: Median neighborhoodMedian Filter for smoothing aroundFiltering Comparison 20 20 1 20 10 20 10 13 13 Special Case: Median Filtering 20 20 1 20 10 20 10 13 13 pixel 20 20 1 image pixel F[i,j] 0 0 200 200 120 2020 10 20 10 13 13 20 20 1 20 0 0 0 0 0 0 20 20 20 20 1 20 10 20 10 13 13 20 0 0 0 0 0 0 20 20 20 0 0 20 2020 20 1 median(20 0 0 0 0 0 0 20)20 median( 0 0 0 1 20 20 20 20 90 ) 90 902090 090 020 020 0 0 0 20 20 20 0 0 20 0 0 0 0 0 1 20 20 20 20 90 = 20 20 0 90 90 90 90 90 20 20 median(20 0 90 90 90 90 90 20)20 median(median( ) median( 0 0 0 1 20 20 ) 20= 20 90 ) 20 0 90 90 90 90 90 20 20 20 0 90 20 200 0 900 0 0 0 1 20=20 2020 20 90 20 0 90 90 90 90 90 20 2020 02090median(0 090 90 90 20 20 ) Medianmedian( = 20 (reMoves outliers) ) = 20 20 0 90 0 90 90 90 20 20 10 0 90 90 90 90 90 10 10 20 0 90 0 0 0 1 20 20 20 20 90 20 0 90 0 90 90 90 20 20 average( ) = 19 20 0 90 0 90 90 90 20 2010 0 90 90 90 90 90 10 10 10 0 90 90 90 90 ©90 2015 Irfan10 Essa,10 Georgia Tech, All Rights Reserved 10 0 90 90 90 90 90 10 10 0 0 0 1 20 20 20 20 90 10 0 90 90 90 90 90 10 10 average( 0 0 0 1 20 20 20 20 90 ) = 19 10 0 90 90 90 90 90 10 1020 0 0 0 0 0 0 20 20 average(F [i,j] 0 0 0 )1 20= 20 1920 20 90 10 0 90 90 90 90 90 10 10 20 20 10 20 10 20 10 13 13 average( ) = 19 10 0 90 90 90 90 90 10 10 Average=171/9 = 19 10 0 90 90 901090 090 9010 9010 90 90 90 10 10 10 0 90 90 90 90 90 10 10 Apply median filter to all 3x3 regions over the 20 0 0 0 0 100 00 9020 9020 90 90 90 10 10 20 0 0 0 0 0 0 20 20 FF [i,j][i,j] • Medianwhole Filterimage :(as Nonlinear we would filter for averaging) 20 20 10 20 102020 010 013 013 0 0 0 20 20 F [i,j] 20 20 10 20 10 20 10 13 13 © 2015 Irfan Essa,– Georgia Reduces Tech, All Rights Reserved noise (the outliers are ‘basically’ noise and 20 20 10 20 10 20 10 13 13 removed).
Load more

Recommended publications
  • A Convolutional Neural Networks Denoising Approach for Salt and Pepper Noise
    A Convolutional Neural Networks Denoising Approach for Salt and Pepper Noise Bo Fu, Xiao-Yang Zhao, Yi Li, Xiang-Hai Wang and Yong-Gong Ren School of Computer and Information Technology, Liaoning Normal University, China [email protected] Abstract. The salt and pepper noise, especially the one with extremely high percentage of impulses, brings a significant challenge to image denoising. In this paper, we propose a non-local switching filter convolutional neural network denoising algorithm, named NLSF-CNN, for salt and pepper noise. As its name suggested, our NLSF-CNN consists of two steps, i.e., a NLSF processing step and a CNN training step. First, we develop a NLSF pre-processing step for noisy images using non-local information. Then, the pre-processed images are divided into patches and used for CNN training, leading to a CNN denoising model for future noisy images. We conduct a number of experiments to evaluate the effectiveness of NLSF-CNN. Experimental results show that NLSF-CNN outperforms the state-of-the-art denoising algorithms with a few training images. Keywords: Image denoising, Salt and pepper noise, Convolutional neural networks, Non-local switching filter. 1 Introduction Images are always polluted by noise during image acquisition and transmission, resulting in low-quality images. The removal of such noise is a must before subsequent image analysis tasks. To achieve this, researchers have proposed many denoising algorithms [1-7], where the representative ones include non-local means (NLM) [1] and block-matching 3D filtering (BM3D) [2].In this paper, we focus on the salt and pepper noise, where pixels exhibit maximal or minimal values with some pre-defined probability.
    [Show full text]
  • 22Nd International Congress on Acoustics ICA 2016
    Page intentionaly left blank 22nd International Congress on Acoustics ICA 2016 PROCEEDINGS Editors: Federico Miyara Ernesto Accolti Vivian Pasch Nilda Vechiatti X Congreso Iberoamericano de Acústica XIV Congreso Argentino de Acústica XXVI Encontro da Sociedade Brasileira de Acústica 22nd International Congress on Acoustics ICA 2016 : Proceedings / Federico Miyara ... [et al.] ; compilado por Federico Miyara ; Ernesto Accolti. - 1a ed . - Gonnet : Asociación de Acústicos Argentinos, 2016. Libro digital, PDF Archivo Digital: descarga y online ISBN 978-987-24713-6-1 1. Acústica. 2. Acústica Arquitectónica. 3. Electroacústica. I. Miyara, Federico II. Miyara, Federico, comp. III. Accolti, Ernesto, comp. CDD 690.22 ISBN 978-987-24713-6-1 © Asociación de Acústicos Argentinos Hecho el depósito que marca la ley 11.723 Disclaimer: The material, information, results, opinions, and/or views in this publication, as well as the claim for authorship and originality, are the sole responsibility of the respective author(s) of each paper, not the International Commission for Acoustics, the Federación Iberoamaricana de Acústica, the Asociación de Acústicos Argentinos or any of their employees, members, authorities, or editors. Except for the cases in which it is expressly stated, the papers have not been subject to peer review. The editors have attempted to accomplish a uniform presentation for all papers and the authors have been given the opportunity to correct detected formatting non-compliances Hecho en Argentina Made in Argentina Asociación de Acústicos Argentinos, AdAA Camino Centenario y 5006, Gonnet, Buenos Aires, Argentina http://www.adaa.org.ar Proceedings of the 22th International Congress on Acoustics ICA 2016 5-9 September 2016 Catholic University of Argentina, Buenos Aires, Argentina ICA 2016 has been organised by the Ibero-american Federation of Acoustics (FIA) and the Argentinian Acousticians Association (AdAA) on behalf of the International Commission for Acoustics.
    [Show full text]
  • Analysis of the Entropy-Guided Switching Trimmed Mean Deviation-Based Anisotropic Diffusion Filter
    Analysis of the Entropy-guided Switching Trimmed Mean Deviation-based Anisotropic Diffusion filter U. A. Nnolim Department of Electronic Engineering, University of Nigeria Nsukka, Enugu, Nigeria Abstract This report describes the experimental analysis of a proposed switching filter-anisotropic diffusion hybrid for the filtering of the fixed value (salt and pepper) impulse noise (FVIN). The filter works well at both low and high noise densities though it was specifically designed for high noise density levels. The filter combines the switching mechanism of decision-based filters and the partial differential equation-based formulation to yield a powerful system capable of recovering the image signals at very high noise levels. Experimental results indicate that the filter surpasses other filters, especially at very high noise levels. Additionally, its adaptive nature ensures that the performance is guided by the metrics obtained from the noisy input image. The filter algorithm is of both global and local nature, where the former is chosen to reduce computation time and complexity, while the latter is used for best results. 1. Introduction Filtering is an imperative and unavoidable process, due to the need for sending or retrieving signals, which are usually corrupted by noise intrinsic to the transmission or reception device or medium. Filtering enables the separation of required and unwanted signals, (which are classified as noise). As a result, filtering is the mainstay of both analog and digital signal and image processing with convolution as the engine of linear filtering processes involving deterministic signals [1] [2]. For nonlinear processes involving non-deterministic signals, order statistics are employed to extract meaningful information [2] [3].
    [Show full text]
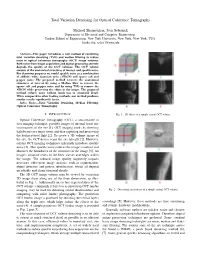
  • Total Variation Denoising for Optical Coherence Tomography
    Total Variation Denoising for Optical Coherence Tomography Michael Shamouilian, Ivan Selesnick Department of Electrical and Computer Engineering, Tandon School of Engineering, New York University, New York, New York, USA fmike.sha, [email protected] Abstract—This paper introduces a new method of combining total variation denoising (TVD) and median filtering to reduce noise in optical coherence tomography (OCT) image volumes. Both noise from image acquisition and digital processing severely degrade the quality of the OCT volumes. The OCT volume consists of the anatomical structures of interest and speckle noise. For denoising purposes we model speckle noise as a combination of additive white Gaussian noise (AWGN) and sparse salt and pepper noise. The proposed method recovers the anatomical structures of interest by using a Median filter to remove the sparse salt and pepper noise and by using TVD to remove the AWGN while preserving the edges in the image. The proposed method reduces noise without much loss in structural detail. When compared to other leading methods, our method produces similar results significantly faster. Index Terms—Total Variation Denoising, Median Filtering, Optical Coherence Tomography I. INTRODUCTION Fig. 1. 2D slices of a sample retinal OCT volume. Optical Coherence Tomography (OCT), a non-invasive in vivo imaging technique, provides images of internal tissue mi- crostructures of the eye [1]. OCT imaging works by directing light beams at a target tissue and then capturing and processing the backscattered light [2]. To create a 3D volume image of the eye, the OCT device scans the eye laterally [2]. However, current OCT imaging techniques inherently introduce speckle noise [3].
    [Show full text]
  • Transportation Noise and Annoyance Related to Road
    Méline et al. International Journal of Health Geographics 2013, 12:44 INTERNATIONAL JOURNAL http://www.ij-healthgeographics.com/content/12/1/44 OF HEALTH GEOGRAPHICS RESEARCH Open Access Transportation noise and annoyance related to road traffic in the French RECORD study Julie Méline1,2*, Andraea Van Hulst3,4, Frédérique Thomas5, Noëlla Karusisi1,2 and Basile Chaix1,2 Abstract Road traffic and related noise is a major source of annoyance and impairment to health in urban areas. Many areas exposed to road traffic noise are also exposed to rail and air traffic noise. The resulting annoyance may depend on individual/neighborhood socio-demographic factors. Nevertheless, few studies have taken into account the confounding or modifying factors in the relationship between transportation noise and annoyance due to road traffic. In this study, we address these issues by combining Geographic Information Systems and epidemiologic methods. Street network buffers with a radius of 500 m were defined around the place of residence of the 7290 participants of the RECORD Cohort in Ile-de-France. Estimated outdoor traffic noise levels (road, rail, and air separately) were assessed at each place of residence and in each of these buffers. Higher levels of exposure to noise were documented in low educated neighborhoods. Multilevel logistic regression models documented positive associations between road traffic noise and annoyance due to road traffic, after adjusting for individual/ neighborhood socioeconomic conditions. There was no evidence that the association was of different magnitude when noise was measured at the place of residence or in the residential neighborhood. However, the strength of the association between neighborhood noise exposure and annoyance increased when considering a higher percentile in the distribution of noise in each neighborhood.
    [Show full text]
  • A Spatial Median Filter for Noise Removal in Digital Images
    A Spatial Median Filter for Noise Removal in Digital Images James Church, Dr. Yixin Chen, and Dr. Stephen Rice Computer Science and Information System, University of Mississippi [email protected],{ychen,rice}@cs.olemiss.edu Abstract Each of the algorithms coveredcan be applied to one di- mensional as well as two dimensional signals. Figure 1 In this paper, six different image filtering algorithms are demonstrates five common filtering algorithms applied compared based on their ability to reconstruct noise- to an original image. affected images. The purpose of these algorithms is to remove noise from a signal that might occur through the transmission of an image. A new algorithm, the Spatial Median Filter, is introduced and compared with the cur- rent image smoothing techniques. Experimental results demonstrate that the proposed algorithm is comparable (a) (b) (c) to popular image smoothing algorithms. In addition, a modification to this algorithm is introduced to achieve more accurate reconstructions over other popular tech- niques. (d) (e) (f) Figure 1. Examples of common filtering ap- 1. Smoothing Algorithms proaches. (a) Original Image (b) Mean Filtering (c) Median Filtering (d) Root signal of Median The inexpensiveness and simplicity of point-and- Filtering (e) Component-wise Median Filtering shoot cameras, combined with the speed at which bud- (f) Vector Median Filtering ding photographerscan send their photos over the Inter- net to be viewed by the world, makes digital photogra- The simplest of smoothing algorithms is the Mean phy a popular hobby. With each snap of a digital pho- Filter as defined in (1). The Mean Filter is a linear filter tograph, a signal is transmitted from a photon sensor which uses a mask over each pixel in the signal.
    [Show full text]
  • 2007 Registration Document
    2007 REGISTRATION DOCUMENT (www.renault.com) REGISTRATION DOCUMENT REGISTRATION 2007 Photos cre dits: cover: Thomas Von Salomon - p. 3 : R. Kalvar - p. 4, 8, 22, 30 : BLM Studio, S. de Bourgies S. BLM Studio, 30 : 22, 8, 4, Kalvar - p. R. 3 : Salomon - p. Von Thomas cover: dits: Photos cre 2007 REGISTRATION DOCUMENT INCLUDING THE MANAGEMENT REPORT APPROVED BY THE BOARD OF DIRECTORS ON FEBRUARY 12, 2008 This Registration Document is on line on the website www .renault.com (French and English versions) and on the AMF website www .amf- france.org (French version only). TABLE OF CONTENTS 0 1 05 RENAULT AND THE GROUP 5 RENAULT AND ITS SHAREHOLDERS 157 1.1 Presentation of Renault and the Group 6 5.1 General information 158 1.2 Risk factors 24 5.2 General information about Renault’s share capital 160 1.3 The Renault-Nissan Alliance 25 5.3 Market for Renault shares 163 5.4 Investor relations policy 167 02 MANAGEMENT REPORT 43 06 2.1 Earnings report 44 MIXED GENERAL MEETING 2.2 Research and development 62 OF APRIL 29, 2008: PRESENTATION 2.3 Risk management 66 OF THE RESOLUTIONS 171 The Board first of all proposes the adoption of eleven resolutions by the Ordinary General Meeting 172 Next, six resolutions are within the powers of 03 the Extraordinary General Meeting 174 SUSTAINABLE DEVELOPMENT 79 Finally, the Board proposes the adoption of two resolutions by the Ordinary General Meeting 176 3.1 Employee-relations performance 80 3.2 Environmental performance 94 3.3 Social performance 109 3.4 Table of objectives (employee relations, environmental
    [Show full text]
  • Noise Reduction by Vector Median Filtering
    GEOPHYSICS, VOL. 78, NO. 3 (MAY-JUNE 2013); P. V79–V86, 18 FIGS., 1 TABLE. 10.1190/GEO2012-0232.1 Noise reduction by vector median filtering Yike Liu1 1984; Marfurt, 2006), Radon transform (Sacchi and Porsani, 1999; ABSTRACT Sacchi et al., 2004), edge-preserving smoothing (Luo et al., 2002), and scalar median filter (SMF) (Mi and Margrave, 2000). Compared The scalar median filter (SMF) is often used to reduce to other methods, the SMF filtering technique often produces less noise in scalar geophysical data. We present an extension smearing among adjacent samples after noise attenuation. For ex- of the SMF to a vector median filter (VMF) for suppressing ample, the SMF can remove an abnormal impulse from seismic re- noise contained in geophysical data represented by multidi- cords without smearing the impulse into its nearby samples as the mensional, multicomponent vector fields. Although the mean or f-k filters do. The SMF can also be used to separate the up- SMF can be applied to each component of a vector field in- and downgoing wavefields in vertical seismic profile (VSP) data dividually, the VMF is applied to all components simulta- because it often reduces interference between these two wavefields. neously. Like the SMF, the VMF intends to suppress Despite the fact that numerous types of geophysical data are random noise while preserving discontinuities in the vector naturally represented by vector fields, the vector median filter fields. Preserving such discontinuities is essential for ex- (VMF) is seldom employed in data processing. On the other hand, ploration geophysics because discontinuities often manifest SMF is commonly used in exploration geophysics.
    [Show full text]
  • Denoising of X-Ray Images Using the Adaptive Algorithm Based on the LPA-RICI Algorithm
    Journal of Imaging Article Denoising of X-ray Images Using the Adaptive Algorithm Based on the LPA-RICI Algorithm Ivica Mandi´c,Hajdi Pei´c,Jonatan Lerga * ID and Ivan Štajduhar Faculty of Engineering, University of Rijeka, Vukovarska 58, 51000 Rijeka, Croatia; [email protected] (I.M.); [email protected] (H.P.); [email protected] (I.Š.) * Correspondence: [email protected]; Tel.: +385-51-651-583 Received: 5 December 2017; Accepted: 2 February 2018; Published: 5 February 2018 Abstract: Diagnostics and treatments of numerous diseases are highly dependent on the quality of captured medical images. However, noise (during both acquisition and transmission) is one of the main factors that reduce their quality. This paper proposes an adaptive image denoising algorithm applied to enhance X-ray images. The algorithm is based on the modification of the intersection of confidence intervals (ICI) rule, called relative intersection of confidence intervals (RICI) rule. For each image pixel apart, a 2D mask of adaptive size and shape is calculated and used in designing the 2D local polynomial approximation (LPA) filters for noise removal. One of the advantages of the proposed method is the fact that the estimation of the noise free pixel is performed independently for each image pixel and thus, the method is applicable for easy parallelization in order to improve its computational efficiency. The proposed method was compared to the Gaussian smoothing filters, total variation denoising and fixed size median filtering and was shown to outperform them both visually and in terms of the peak signal-to-noise ratio (PSNR) by up to 7.99 dB.
    [Show full text]
  • Transportation Noise and Annoyance Related to Road Traffic
    Transportation noise and annoyance related to road traffic in the French RECORD study. Julie Méline, Andraea van Hulst, Frédérique Thomas, Noëlla Karusisi, Basile Chaix To cite this version: Julie Méline, Andraea van Hulst, Frédérique Thomas, Noëlla Karusisi, Basile Chaix. Transportation noise and annoyance related to road traffic in the French RECORD study.. International Journal of Health Geographics, BioMed Central, 2013, 12 (1), pp.44. 10.1186/1476-072X-12-44. inserm- 00870153 HAL Id: inserm-00870153 https://www.hal.inserm.fr/inserm-00870153 Submitted on 5 Oct 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Méline et al. International Journal of Health Geographics 2013, 12:44 INTERNATIONAL JOURNAL http://www.ij-healthgeographics.com/content/12/1/44 OF HEALTH GEOGRAPHICS RESEARCH Open Access Transportation noise and annoyance related to road traffic in the French RECORD study Julie Méline1,2*, Andraea Van Hulst3,4, Frédérique Thomas5, Noëlla Karusisi1,2 and Basile Chaix1,2 Abstract Road traffic and related noise is a major source of annoyance and impairment to health in urban areas. Many areas exposed to road traffic noise are also exposed to rail and air traffic noise.
    [Show full text]
  • Median Filtering by Threshold Decomposition: Induction Proof
    Median Filtering by Threshold Decomposition: Induction Proof by Connor Bramham, Brandon Mayle, Maura Gallagher, Douglas Magruder, and Cooper Reep Math Club Socrates Preparatory School www.socprep.org [email protected] Sponsors: Saul Rubin and Neal C. Gallagher, Ph.D, Socrates Preparatory School, 3955 Red Bug Lake Rd., Casselberry, FL 32707 [email protected] [email protected] Abstract In building a robot for the FTC competition, our team needed to remove motor noise from our sensor signals. So we settled on using a median filter because of the medians superior removal of impulsive noise. For us, however, the foundational publications that describe these filters were challenging to understand. Having learned the concept of proof by induction from the MIT OpenCourseWare course, “Mathematics for Computer Science” (MIT Course Number 6.042J / 18.062J), we developed an original proof for the principle of median filter threshold decomposition in order to better understand their operation. The induction is over the number of quantized threshold levels for the sequence of input values as applied to both the standard and recursive median filter. I Introduction Many of this paper’s authors participated in the 2017 First Tech Challenge robotics competition. Our completed robot contained many motors and sensors, including ultrasound sensors for distance measurements, gyroscopic sensors for direction measurements, color sensors to sense the brightness and color of beacons, and more. The robot’s electric motors generated a considerable amount of noise that found its way onto the signals from our sensors to our robot controller. One method used to address the noise problem is to use an aluminum sheet to shield robot electronics from the drive motors and servos, but more was needed.
    [Show full text]
  • Blind Denoising by Self-Supervision
    Noise2Self: Blind Denoising by Self-Supervision Joshua Batson * 1 Loic Royer * 1 Abstract highly correlated. Speaking loosely, if the “latent dimen- We propose a general framework for denoising sion” of the space of objects under study is much lower than high-dimensional measurements which requires the dimension of the measurement, it may be possible to no prior on the signal, no estimate of the noise, implicitly learn that structure, denoise the measurements, and no clean training data. The only assumption and recover the signal without any prior knowledge of the is that the noise exhibits statistical independence signal or the noise. across different dimensions of the measurement, Traditional denoising methods each exploit a property of while the true signal exhibits some correlation. the noise, such as Gaussianity, or structure in the signal, For a broad class of functions (“J -invariant”), it such as spatiotemporal smoothness, self-similarity, or hav- is then possible to estimate the performance of ing low-rank. The performance of these methods is limited a denoiser from noisy data alone. This allows by the accuracy of their assumptions. For example, if the us to calibrate J -invariant versions of any pa- data are genuinely not low rank, then a low rank model rameterised denoising algorithm, from the single will fit it poorly. This requires prior knowledge of the sig- hyperparameter of a median filter to the millions nal structure, which limits application to new domains and of weights of a deep neural network. We demon- modalities. These methods also require calibration, as hy- strate this on natural image and microscopy data, perparameters such as the degree of smoothness, the scale of where we exploit noise independence between self-similarity, or the rank of a matrix have dramatic impacts pixels, and on single-cell gene expression data, on performance.
    [Show full text]