DOCSLIB.ORG

HILTON Umd 0117E 21218.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
HILTON Umd 0117E 21218.Pdf ABSTRACT Title of Dissertation: GENETICS, AGES, AND CHEMICAL COMPOSITIONS OF IRON METEORITES Connor Hilton, Doctor of Philosophy, 2020 Dissertation directed by: Professor Richard Walker, Department of Geology Comparison of genetic isotopic compositions of iron meteorites with metal- silicate segregation ages suggests that the isotopic composition of the NC reservoir changed with time. By contrast, no such age-linked changes in the genetic isotopic compositions of iron meteorites from the CC reservoir are observed. Results of comparing bulk planetesimal genetic isotopic compositions with bulk planetesimal siderophile element chemical characteristics indicate that the processes responsible for isotopic heterogeneity in the early Solar System are not discerned by the siderophile element chemical characteristics of planetesimals. Iron meteorite parent bodies from the CC reservoir typically have smaller relative cores and a greater proportion of the Fe content in the mantle, consistent with the CC reservoir being a more oxidized environment, such as the outer Solar System, compared to the NC reservoir. The chemical characteristics of iron meteorite parent bodies, including bulk core FeS/Fe ratios and oxidation states, may form relationships with core formation ages, but whether these characteristics can account for potential differences in the formation ages of NC- and CC-type parent bodies presently cannot be constrained. GENETICS, AGES, AND CHEMICAL COMPOSITIONS OF IRON METEORITES by Connor D. Hilton Dissertation submitted to the Faculty of the Graduate School of the University of Maryland, College Park, in partial fulfillment of the requirements for the degree of Doctor of Philosophy 2020 Advisory Committee: Professor Richard J. Walker, Chair Associate Professor Ricardo D. Arevalo Research Scientist Richard D. Ash Dr. Timothy J. McCoy Professor Alice Mignerey (Dean’s Representative) © Copyright by Connor Hilton 2020 Preface Portions of this dissertation have been previously published in peer-reviewed journals or are currently in preparation or revision. Specifically, chapters 2 and 3 have been published. Chapters 4 and 5 are currently in revision and in preparation, respectively. The contributions of each co-author to each chapter of this dissertation are outlined here. Chapter 2 Hilton C.D., Bermingham K.R., Walker R.J., McCoy T.J. (2019) Genetics, crystallization sequence, and age of the South Byron Trio iron meteorites: New insights to carbonaceous chondrite (CC) type parent bodies. Geochim. Cosmochim. Acta 251, 217-228. In this study, I collected all Os, Mo, Ru, and W isotope data and performed all trace element and thermal modeling. Katherine Bermingham provided guidance in the laboratory and Rich Walker collected the highly siderophile element and 187Os isotope data. Tim McCoy helped interpret the data. I wrote the first draft of this manuscript and edits were provided by co-authors. Chapter 3 Hilton C.D. and Walker R.J. (2020) New implications for the origin of the IAB main group iron meteorites and the isotopic evolution of the noncarbonaceous (NC) reservoir. Earth Planet. Sci. Lett. 540, 116248. ii I collected all Os, Pt, and W isotope data and wrote the first draft of this manuscript. Rich Walker helped interpret the data and edit the manuscript. Chapter 4 Hilton C.D., Ash R.D., and Walker R.J. (In revision) Origin of the Eagle Station Pallasites from the IIF iron meteorite core. Meteorit. Planet. Sci. In this study, I collected all highly siderophile element and Os isotope data and performed all trace element modeling. Richard Ash collected the siderophile element abundances by LA-ICP-MS. I interpreted all data and wrote the first draft of this manuscript. Richard Ash and Rich Walker provided edits. Chapter 5 Hilton C.D, Ash R.D., and Walker R.J. (In prep) Constraints on the chemical characteristics of the noncarbonaceous (NC) and carbonaceous (CC) nebular reservoirs. I collected highly siderophile element and Os isotope data for the IIAB, IID, and IIIF iron meteorites and performed all trace element modeling. The highly siderophile element and Os isotope data for the IIIAB iron meteorites were collected by a previous student under the supervision of Rich Walker. I interpreted all data and wrote the first draft of this manuscript. Richard Ash and Rich Walker provided edits. iii Acknowledgements I would like to thank Rich Walker, Ricardo Arevalo, Richard Ash, Tim McCoy, and Alice Mignerey for serving on my PhD committee as well as reading my dissertation and providing feedback. Rich Walker, Ricardo Arevalo, Richard Ash, and Tim McCoy are additionally thanked for their support throughout the proposal process and for their guidance over the course of this PhD. I am grateful for the funding provided by the University of Maryland and NASA for this dissertation and thankful for the meteorites provided to me by Arizona State University, the Cascadia Meteorite Laboratory, the Field Museum, the Maine Mineral and Gem Museum, the Russian Academy of Sciences, the Smithsonian Institution, and the University of California-Los Angeles. Rich Walker is especially recognized for his role as my PhD advisor and for all the work that entails. I am also grateful for the guidance and friendship that I have received from Richard Ash and Igor Puchtel, and for the support given to me by Michelle Montero, Suzanne Martin, and Todd Karwoski throughout graduate school. The past and present members of the Isotope Geochemistry Laboratory group, including Greg Archer, Katherine Bermingham, Emily Chiappe, Val Finlayson, Mitch Haller, Andi Mundl- Petermeier, Nao Nakanishi, Willie Nicklas, Hope Tornabene, and Emily Worsham, are thanked for their support and advice. I have fond memories of graduate school and, for that, I thank my fellow graduate students as well as the UMD Geology faculty and staff. I could not have completed my PhD without the support of my family, in particular my mother and sister, as well as my friends, old and new. Finally, I thank my fiancée, Anya, for her love and support, which iv helped me through this process immensely. I met Anya within the first two months of graduate school and she has been with me on this journey ever since. v Table of Contents Preface................................................................................................................................. ii Acknowledgements ............................................................................................................ iv Table of Contents ............................................................................................................... vi List of Tables ................................................................................................................... viii List of Figures .................................................................................................................... ix List of Abbreviations ........................................................................................................ xii Chapter 1: Introduction and Goals ...................................................................................... 1 1.1 Driving questions ...................................................................................................... 1 1.2 Background ............................................................................................................... 1 1.3 Research goals .......................................................................................................... 7 Chapter 2: Genetics, crystallization sequence, and age of the South Byron Trio iron meteorites: New insights to carbonaceous chondrite (CC) type parent bodies .................. 9 2.1 Abstract ..................................................................................................................... 9 2.2 Introduction ............................................................................................................. 10 2.3 Materials and methods ............................................................................................ 13 2.4 Results ..................................................................................................................... 16 2.5 Discussion ............................................................................................................... 22 2.6 Conclusions ............................................................................................................. 39 2.7 Acknowledgements ................................................................................................. 41 2.8 Appendix 2 .............................................................................................................. 41 Chapter 3: New implications for the origin of the IAB main group iron meteorites and the isotopic evolution of the noncarbonaceous (NC) reservoir .............................................. 56 3.1 Abstract ................................................................................................................... 56 3.2 Introduction ............................................................................................................. 57 3.3 Methods................................................................................................................... 61 3.4 Results ..................................................................................................................... 64 3.5 Discussion ..............................................................................................................
Load more

Recommended publications
  • Meteorites on Mars Observed with the Mars Exploration Rovers C
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 113, E06S22, doi:10.1029/2007JE002990, 2008 Meteorites on Mars observed with the Mars Exploration Rovers C. Schro¨der,1 D. S. Rodionov,2,3 T. J. McCoy,4 B. L. Jolliff,5 R. Gellert,6 L. R. Nittler,7 W. H. Farrand,8 J. R. Johnson,9 S. W. Ruff,10 J. W. Ashley,10 D. W. Mittlefehldt,1 K. E. Herkenhoff,9 I. Fleischer,2 A. F. C. Haldemann,11 G. Klingelho¨fer,2 D. W. Ming,1 R. V. Morris,1 P. A. de Souza Jr.,12 S. W. Squyres,13 C. Weitz,14 A. S. Yen,15 J. Zipfel,16 and T. Economou17 Received 14 August 2007; revised 9 November 2007; accepted 21 December 2007; published 18 April 2008. [1] Reduced weathering rates due to the lack of liquid water and significantly greater typical surface ages should result in a higher density of meteorites on the surface of Mars compared to Earth. Several meteorites were identified among the rocks investigated during Opportunity’s traverse across the sandy Meridiani plains. Heat Shield Rock is a IAB iron meteorite and has been officially recognized as ‘‘Meridiani Planum.’’ Barberton is olivine-rich and contains metallic Fe in the form of kamacite, suggesting a meteoritic origin. It is chemically most consistent with a mesosiderite silicate clast. Santa Catarina is a brecciated rock with a chemical and mineralogical composition similar to Barberton. Barberton, Santa Catarina, and cobbles adjacent to Santa Catarina may be part of a strewn field. Spirit observed two probable iron meteorites from its Winter Haven location in the Columbia Hills in Gusev Crater.
    [Show full text]
  • Handbook of Iron Meteorites, Volume 2 (Canyon Diablo, Part 2)
    Canyon Diablo 395 The primary structure is as before. However, the kamacite has been briefly reheated above 600° C and has recrystallized throughout the sample. The new grains are unequilibrated, serrated and have hardnesses of 145-210. The previous Neumann bands are still plainly visible , and so are the old subboundaries because the original precipitates delineate their locations. The schreibersite and cohenite crystals are still monocrystalline, and there are no reaction rims around them. The troilite is micromelted , usually to a somewhat larger extent than is present in I-III. Severe shear zones, 100-200 J1 wide , cross the entire specimens. They are wavy, fan out, coalesce again , and may displace taenite, plessite and minerals several millimeters. The present exterior surfaces of the slugs and wedge-shaped masses have no doubt been produced in a similar fashion by shear-rupture and have later become corroded. Figure 469. Canyon Diablo (Copenhagen no. 18463). Shock­ The taenite rims and lamellae are dirty-brownish, with annealed stage VI . Typical matte structure, with some co henite crystals to the right. Etched. Scale bar 2 mm. low hardnesses, 160-200, due to annealing. In crossed Nicols the taenite displays an unusual sheen from many small crystals, each 5-10 J1 across. This kind of material is believed to represent shock­ annealed fragments of the impacting main body. Since the fragments have not had a very long flight through the atmosphere, well developed fusion crusts and heat-affected rim zones are not expected to be present. The energy responsible for bulk reheating of the small masses to about 600° C is believed to have come from the conversion of kinetic to heat energy during the impact and fragmentation.
    [Show full text]
  • Evolution of Asteroidal Cores 747
    Chabot and Haack: Evolution of Asteroidal Cores 747 Evolution of Asteroidal Cores N. L. Chabot The Johns Hopkins Applied Physics Laboratory H. Haack University of Copenhagen Magmatic iron meteorites provide the opportunity to study the central metallic cores of aster- oid-sized parent bodies. Samples from at least 11, and possibly as many as 60, different cores are currently believed to be present in our meteorite collections. The cores crystallized within 100 m.y. of each other, and the presence of signatures from short-lived isotopes indicates that the crystallization occurred early in the history of the solar system. Cooling rates are generally consistent with a core origin for many of the iron meteorite groups, and the most current cooling rates suggest that cores formed in asteroids with radii of 3–100 km. The physical process of core crystallization in an asteroid-sized body could be quite different than in Earth, with core crystallization probably initiated by dendrites growing deep into the core from the base of the mantle. Utilizing experimental partitioning values, fractional crystallization models have ex- amined possible processes active during the solidification of asteroidal cores, such as dendritic crystallization, assimilation of new material during crystallization, incomplete mixing in the molten core, the onset of liquid immiscibility, and the trapping of melt during crystallization. 1. INTRODUCTION ture of the metal and the presence of secondary minerals, are also considered (Scott and Wasson, 1975). In the first From Mercury to the moons of the outer solar system, attempt to classify iron meteorites, groups I–IV were de- central metallic cores are common in the planetary bodies fined on the basis of their Ga and Ge concentrations.
    [Show full text]
  • THE Hf-W ISOTOPIC SYSTEM and the ORIGIN of the EARTH and MOON
    18 Mar 2005 11:55 AR AR233-EA33-18.tex XMLPublishSM(2004/02/24) P1: KUV 10.1146/annurev.earth.33.092203.122614 Annu. Rev. Earth Planet. Sci. 2005. 33:531–70 doi: 10.1146/annurev.earth.33.092203.122614 Copyright c 2005 by Annual Reviews. All rights reserved First published online as a Review in Advance on February 1, 2005 THE Hf-W ISOTOPIC SYSTEM AND THE ORIGIN OF THE EARTH AND MOON Stein B. Jacobsen Department of Earth and Planetary Sciences, Harvard University, Cambridge, Massachusetts 02138; email: [email protected] KeyWords accretion, tungsten, isotopes, chronometer, core formation ■ Abstract The Earth has a radiogenic W-isotopic composition compared to chon- drites, demonstrating that it formed while 182Hf (half-life 9 Myr) was extant in Earth and decaying to 182W. This implies that Earth underwent early and rapid accretion and core formation, with most of the accumulation occurring in ∼10 Myr, and concluding approximately 30 Myr after the origin of the Solar System. The Hf-W data for lunar samples can be reconciled with a major Moon-forming impact that terminated the ter- restrial accretion process ∼30 Myr after the origin of the Solar System. The suggestion that the proto-Earth to impactor mass ratio was 7:3 and occurred during accretion is inconsistent with the W isotope data. The W isotope data is satisfactorily modeled with a Mars-sized impactor on proto-Earth (proto-Earth to impactor ratio of 9:1) to form the Moon at ∼30 Myr. 1. INTRODUCTION The process of terrestrial planet-building probably began when a large population of small bodies (planetesimals) of roughly similar size coagulated into a smaller population of larger bodies.
    [Show full text]
  • Trace Element Chemistry of Cumulus Ridge 04071 Pallasite with Implications for Main Group Pallasites
    Trace element chemistry of Cumulus Ridge 04071 pallasite with implications for main group pallasites Item Type Article; text Authors Danielson, L. R.; Righter, K.; Humayun, M. Citation Danielson, L. R., Righter, K., & Humayun, M. (2009). Trace element chemistry of Cumulus Ridge 04071 pallasite with implications for main group pallasites. Meteoritics & Planetary Science, 44(7), 1019-1032. DOI 10.1111/j.1945-5100.2009.tb00785.x Publisher The Meteoritical Society Journal Meteoritics & Planetary Science Rights Copyright © The Meteoritical Society Download date 23/09/2021 14:17:54 Item License http://rightsstatements.org/vocab/InC/1.0/ Version Final published version Link to Item http://hdl.handle.net/10150/656592 Meteoritics & Planetary Science 44, Nr 7, 1019–1032 (2009) Abstract available online at http://meteoritics.org Trace element chemistry of Cumulus Ridge 04071 pallasite with implications for main group pallasites Lisa R. DANIELSON1*, Kevin RIGHTER2, and Munir HUMAYUN3 1Mailcode JE23, NASA Johnson Space Center, 2101 NASA Parkway, Houston, Texas 77058, USA 2Mailcode KT, NASA Johnson Space Center, 2101 NASA Parkway, Houston, Texas 77058, USA 3National High Magnetic Field Laboratory and Department of Geological Sciences, Florida State University, Tallahassee, Florida 32310, USA *Corresponding author. E-mail: [email protected] (Received 06 November 2008; revision accepted 11 May 2009) Abstract–Pallasites have long been thought to represent samples from the metallic core–silicate mantle boundary of a small asteroid-sized body, with as many as ten different parent bodies recognized recently. This report focuses on the description, classification, and petrogenetic history of pallasite Cumulus Ridge (CMS) 04071 using electron microscopy and laser ablation ICP-MS.
    [Show full text]
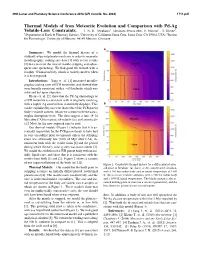
  • Thermal Models of Iron Meteorite Evolution and Comparison with Pd-Ag Volatile-Loss Constraints
    49th Lunar and Planetary Science Conference 2018 (LPI Contrib. No. 2083) 1711.pdf Thermal Models of Iron Meteorite Evolution and Comparison with Pd-Ag Volatile-Loss Constraints. J. N. H. Abrahams1 ([email protected]), F. Nimmo1, T. Kleine2, 1Department of Earth & Planetary Science, University of California Santa Cruz, Santa Cruz, CA 95064, USA, 2Institut fur¨ Planetologie, University of Munster,¨ 48149 Munster,¨ Germany Summary: We model the thermal history of a suddenly-exposed planetesimal core in order to reconcile metallographic cooling rate data [1] with recent results [2] that constrain the time of mantle stripping and subse- quent core quenching. We find good fits to both with a roughly 40 km iron body which is entirely molten when it is first exposed. Introduction: Yang et. al. [1] measured metallo- graphic cooling rates of IVB meteorites and showed they were broadly consistent with a ∼65 km body which was solid and hot upon exposure. Kleine et. al. [2] show that the Pd-Ag chronology of a IVB meteorite is consistent with it originally evolving with a higher Ag content than it currently displays. This can be explained by an event that reduced the IVB parent body’s volatile content, which we assume to be the catas- trophic disruption event. The data suggest a time (8-14 Myr after CAI formation) of volatile loss and a timescale (≤2 Myr) for the now-exposed core to cool. Our thermal models (Figure 1) indicate that it is es- sentially impossible for the IVB parent body to have had its core crystallize prior to exposure unless the stripping event was extremely late (100s of Myr after CAI), in- consistent both with the results from [2] and the period during which the early solar system was most violent [3].
    [Show full text]
  • Compiled Thesis
    SPACE ROCKS: a series of papers on METEORITES AND ASTEROIDS by Nina Louise Hooper A thesis submitted to the Department of Astronomy in partial fulfillment of the requirement for the Bachelor’s Degree with Honors Harvard College 8 April 2016 Of all investments into the future, the conquest of space demands the greatest efforts and the longest-term commitment, but it also offers the greatest reward: none less than a universe. — Daniel Christlein !ii Acknowledgements I finished this senior thesis aided by the profound effort and commitment of my thesis advisor, Martin Elvis. I am extremely grateful for him countless hours of discussions and detailed feedback on all stages of this research. I am also grateful for the remarkable people at Harvard-Smithsonian Center for Astrophysics of whom I asked many questions and who took the time to help me. Special thanks go to Warren Brown for his guidance with spectral reduction processes in IRAF, Francesca DeMeo for her assistance in the spectral classification of our Near Earth Asteroids and Samurdha Jayasinghe and for helping me write my data analysis script in python. I thank Dan Holmqvist for being an incredibly helpful and supportive presence throughout this project. I thank David Charbonneau, Alicia Soderberg and the members of my senior thesis class of astrophysics concentrators for their support, guidance and feedback throughout the past year. This research was funded in part by the Harvard Undergraduate Science Research Program. !iii Abstract The subject of this work is the compositions of asteroids and meteorites. Studies of the composition of small Solar System bodies are fundamental to theories of planet formation.
    [Show full text]
  • Asteroid Differentiation 733
    McCoy et al.: Asteroid Differentiation 733 Asteroid Differentiation Timothy J. McCoy Smithsonian Institution David W. Mittlefehldt NASA Johnson Space Center Lionel Wilson University of Hawai‘i at Manoa Differentiation of silicate bodies was widespread in the inner solar system, producing an array of igneous meteorites. While the precursor material was certainly chondritic, direct links between chondrites and achondrites are few and tenuous. Heating by short-lived radionuclides (26Al and 60Fe) initiated melting. Formation of a basaltic crust would occur soon after the onset of melting, as would migration of the cotectic Fe,Ni-FeS component, perhaps forming a S-rich core. While some asteroids appear to be arrested at this point, many continued to heat up, with efficient segregation of metal to form large cores. Extensive melting of the silicate mantle oc- curred, perhaps reaching 40–75%. In the largest asteroids, the original, basaltic crust may have been resorbed into the mantle, producing a magma ocean. The crystallization of that magma ocean, whether by equilibrium or fractional crystallization, could have produced the layered structure typical of large differentiated asteroids like 4 Vesta. Spacecraft exploration of 4 Vesta promises to further extend our knowledge of asteroid differentiation. 1. INTRODUCTION and over a broader range of states of hydration. Thus, studies of asteroidal differentiation provide a natural complement The transformation of rocky bodies from an agglomer- to studies of igneous systems under terrestrial conditions. ate of nebular particles to fully differentiated, layered worlds Despite the obvious interest in asteroid differentiation, consisting of core, mantle, and crust is, without question, a complete understanding of this process has been and re- one of the most fundamental processes to have occurred mains elusive, in large part owing to the remoteness in time during the birth of our solar system.
    [Show full text]
  • Constraints on Nebular and Parent Body Processes from Iron Meteorites
    Research Collection Doctoral Thesis Palladium Isotope Cosmochemistry: Constraints on Nebular and Parent Body Processes from Iron Meteorites Author(s): Ek, Mattias Publication Date: 2018 Permanent Link: https://doi.org/10.3929/ethz-b-000265291 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library DISS. ETH NO. 24810 PALLADIUM ISOTOPE COSMOCHEMISTRY: CONSTRAINTS ON NEBULAR AND PARENT BODY PROCESSES FROM IRON METEORITES A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by PAÄR KARL MATTIAS EK MSc in Earth Sciences, Göteborgs Universitet Citizen of Sweden Born on August 11, 1988 accepted on the recommendation of Prof. Dr. Mark Rehkämper Dr. Alison C. Hunt Dr. Maria Lugaro Prof. Dr. Maria Schönbächler 2018 Contents Abstract Zussamenfassung v Chapter 1 vii An introduction to cosmochemistry 1 1.1. A brief history of the universe 2 1.1.1. The Big Bang and primordial nucleosynthesis 2 1.1.2. Stellar evolution and nucleosynthesis 3 1.1.3. Solar system evolution 6 1.1.4. Early Earth History 8 1.1.5. The Meteorite record 9 1.2. Isotopic variations in meteorites 10 1.2.1. The origin of mass-independent isotopic variations in the solar nebula 11 1.2.2. Parent body processes and mass-dependent isotopic fractionation 13 1.3. Thesis outline 14 Chapter 2 Initial separation of Pd and Pt from iron meteorites using ion exchange chromatography 17 2.1. Introduction 18 2.2.
    [Show full text]
  • Mars: an Introduction to Its Interior, Surface and Atmosphere
    MARS: AN INTRODUCTION TO ITS INTERIOR, SURFACE AND ATMOSPHERE Our knowledge of Mars has changed dramatically in the past 40 years due to the wealth of information provided by Earth-based and orbiting telescopes, and spacecraft investiga- tions. Recent observations suggest that water has played a major role in the climatic and geologic history of the planet. This book covers our current understanding of the planet’s formation, geology, atmosphere, interior, surface properties, and potential for life. This interdisciplinary text encompasses the fields of geology, chemistry, atmospheric sciences, geophysics, and astronomy. Each chapter introduces the necessary background information to help the non-specialist understand the topics explored. It includes results from missions through 2006, including the latest insights from Mars Express and the Mars Exploration Rovers. Containing the most up-to-date information on Mars, this book is an important reference for graduate students and researchers. Nadine Barlow is Associate Professor in the Department of Physics and Astronomy at Northern Arizona University. Her research focuses on Martian impact craters and what they can tell us about the distribution of subsurface water and ice reservoirs. CAMBRIDGE PLANETARY SCIENCE Series Editors Fran Bagenal, David Jewitt, Carl Murray, Jim Bell, Ralph Lorenz, Francis Nimmo, Sara Russell Books in the series 1. Jupiter: The Planet, Satellites and Magnetosphere Edited by Bagenal, Dowling and McKinnon 978 0 521 81808 7 2. Meteorites: A Petrologic, Chemical and Isotopic Synthesis Hutchison 978 0 521 47010 0 3. The Origin of Chondrules and Chondrites Sears 978 0 521 83603 6 4. Planetary Rings Esposito 978 0 521 36222 1 5.
    [Show full text]
  • Catalogue of the National Meteorite Collection of Canada Revised to December 31, 1979
    GEOLOGICAL SURVEY OF CANADA COMMISSION GEOLOGIQUE DU CANADA PAPER 80-17 CATALOGUE OF THE NATIONAL METEORITE COLLECTION OF CANADA REVISED TO DECEMBER 31, 1979 R.J. TRAILL Energy, Mines and Energie, Mines et I+ Resources Canada Ressources Canada 1980 GEOLOGICAL SURVEY PAPER 80-17 CATALOGUE OF THE NATIONAL METEORITE COLLECTION OF CANADA REVISED TO DECEMBER 31, 1979 R.J. TRAILL 1980 © Minister of Supply and Services Canada 1980 Available in Canada through authorized book store agents and other bookstores or by mail from Canadian Government Publishing Centre Supply and Services Canada HuJJ, Quebec, Canada Kl A OS9 and from Geological Survey of Canada 60 l Booth Street Ottawa, Canada Kl A OE8 A deposit copy of this publication is also available for reference in public libraries across Canada Cat. No. M44-80/ l 7E Canada: $3.00 ISBN - 0-660-10636-1 Other countries: $3.60 Price subject to change without notice CATALOGUE OF THE NATIONAL METEORITE COLLECTION OF CANADA REVISED TO DECEMBER 31, 1979 INTRODUCTION INTRODUCTION The National Meteorite CoJJection was initiated by the La Collection nationale de meteorites voit le jour en Geological Survey of Canada in 1855 with the acquisition of 1855, lorsque la Commission geologique du Canada fait MADOC, Ontario, the first meteorite to be found in Canada. !'acquisition du meteorite MADOC (Ontario), le premier a From 1855 to 1914 a small number of new Canadian finds etre trouve au Canada. De 1855 a J 914, un petit nombre de were added. Status as an international collection was gained meteorites nouveaux trouves au Canada viennent s'y ajouter.
    [Show full text]
  • Meteorite Cloudy Zone Formation As a Quantitative Indicator of Paleomagnetic Field Intensities and Cooling Rates on Planetesimal
    Earth and Planetary Science Letters 513 (2019) 166–175 Contents lists available at ScienceDirect Earth and Planetary Science Letters www.elsevier.com/locate/epsl Meteorite cloudy zone formation as a quantitative indicator of paleomagnetic field intensities and cooling rates on planetesimals ∗ Clara Maurel a, , Benjamin P. Weiss a, James F.J. Bryson b a Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA b Department of Earth Sciences, University of Cambridge, Cambridge, UK a r t i c l e i n f o a b s t r a c t Article history: Metallic microstructures in slowly-cooled iron-rich meteorites reflect the thermal and magnetic histories Received 4 September 2018 of their parent planetesimals. Of particular interest is the cloudy zone, a nanoscale intergrowth of Ni- Received in revised form 29 January 2019 ◦ rich islands within a Ni-poor matrix that forms below ∼350 C by spinodal decomposition. The sizes Accepted 20 February 2019 of the islands have long been recognized as reflecting the low-temperature cooling rates of meteorite Available online xxxx parent bodies. However, a model capable of providing quantitative cooling rate estimates from island Editor: F. Moynier sizes has been lacking. Moreover, these islands are also capable of preserving a record of the ambient Keywords: magnetic field as they grew, but some of the key physical parameters required for recovering reliable planetesimals paleointensity estimates from magnetic measurements of these islands have been poorly constrained. iron meteorites To address both of these issues, we present a numerical model of the structural and compositional cloudy zone evolution of the cloudy zone as a function of cooling rate and local composition.
    [Show full text]