Nonobtuse Local Tetrahedral Refinements Towards a Polygonal
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Volumes of Prisms and Cylinders 625
11-4 11-4 Volumes of Prisms and 11-4 Cylinders 1. Plan Objectives What You’ll Learn Check Skills You’ll Need GO for Help Lessons 1-9 and 10-1 1 To find the volume of a prism 2 To find the volume of • To find the volume of a Find the area of each figure. For answers that are not whole numbers, round to prism a cylinder the nearest tenth. • To find the volume of a 2 Examples cylinder 1. a square with side length 7 cm 49 cm 1 Finding Volume of a 2. a circle with diameter 15 in. 176.7 in.2 . And Why Rectangular Prism 3. a circle with radius 10 mm 314.2 mm2 2 Finding Volume of a To estimate the volume of a 4. a rectangle with length 3 ft and width 1 ft 3 ft2 Triangular Prism backpack, as in Example 4 2 3 Finding Volume of a Cylinder 5. a rectangle with base 14 in. and height 11 in. 154 in. 4 Finding Volume of a 6. a triangle with base 11 cm and height 5 cm 27.5 cm2 Composite Figure 7. an equilateral triangle that is 8 in. on each side 27.7 in.2 New Vocabulary • volume • composite space figure Math Background Integral calculus considers the area under a curve, which leads to computation of volumes of 1 Finding Volume of a Prism solids of revolution. Cavalieri’s Principle is a forerunner of ideas formalized by Newton and Leibniz in calculus. Hands-On Activity: Finding Volume Explore the volume of a prism with unit cubes. -

Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions
Section 11-4 Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a given distance from a given point, the center . A sphere is a simple closed surface. A solid is a simple closed surface with all interior points. (see p. 726) A polyhedron is a simple closed surface made up of polygonal regions, or faces . The vertices of the polygonal regions are the vertices of the polyhedron, and the sides of each polygonal region are the edges of the polyhedron. (see p. 726-727) A prism is a polyhedron in which two congruent faces lie in parallel planes and the other faces are bounded by parallelograms. The parallel faces of a prism are the bases of the prism. A prism is usually names after its bases. The faces other than the bases are the lateral faces of a prism. A right prism is one in which the lateral faces are all bounded by rectangles. An oblique prism is one in which some of the lateral faces are not bounded by rectangles. To draw a prism: 1) Draw one of the bases. 2) Draw vertical segments of equal length from each vertex. 3) Connect the bottom endpoints to form the second base. Use dashed segments for edges that cannot be seen. A pyramid is a polyhedron determined by a polygon and a point not in the plane of the polygon. The pyramid consists of the triangular regions determined by the point and each pair of consecutive vertices of the polygon and the polygonal region determined by the polygon. -

10-4 Surface and Lateral Area of Prism and Cylinders.Pdf
Aim: How do we evaluate and solve problems involving surface area of prisms an cylinders? Objective: Learn and apply the formula for the surface area of a prism. Learn and apply the formula for the surface area of a cylinder. Vocabulary: lateral face, lateral edge, right prism, oblique prism, altitude, surface area, lateral surface, axis of a cylinder, right cylinder, oblique cylinder. Prisms and cylinders have 2 congruent parallel bases. A lateral face is not a base. The edges of the base are called base edges. A lateral edge is not an edge of a base. The lateral faces of a right prism are all rectangles. An oblique prism has at least one nonrectangular lateral face. An altitude of a prism or cylinder is a perpendicular segment joining the planes of the bases. The height of a three-dimensional figure is the length of an altitude. Surface area is the total area of all faces and curved surfaces of a three-dimensional figure. The lateral area of a prism is the sum of the areas of the lateral faces. Holt Geometry The net of a right prism can be drawn so that the lateral faces form a rectangle with the same height as the prism. The base of the rectangle is equal to the perimeter of the base of the prism. The surface area of a right rectangular prism with length ℓ, width w, and height h can be written as S = 2ℓw + 2wh + 2ℓh. The surface area formula is only true for right prisms. To find the surface area of an oblique prism, add the areas of the faces. -

Year 6 – Wednesday 24Th June 2020 – Maths
1 Year 6 – Wednesday 24th June 2020 – Maths Can I identify 3D shapes that have pairs of parallel or perpendicular edges? Parallel – edges that have the same distance continuously between them – parallel edges never meet. Perpendicular – when two edges or faces meet and create a 90o angle. 1 4. 7. 10. 2 5. 8. 11. 3. 6. 9. 12. C1 – Using the shapes above: 1. Name and sort the shapes into: a. Pyramids b. Prisms 2. Draw a table to identify how many faces, edges and vertices each shape has. 3. Write your own geometric definition: a. Prism b. pyramid 4. Which shape is the odd one out? Explain why. C2 – Using the shapes above; 1. Which of the shapes have pairs of parallel edges in: a. All their faces? b. More than one half of the faces? c. One face only? 2. The following shapes have pairs of perpendicular edges. Identify the faces they are in: 2 a. A cube b. A square based pyramid c. A triangular prism d. A cuboid 3. Which shape with straight edges has no perpendicular edges? 4. Which shape has perpendicular edges in the shape but not in any face? C3 – Using the above shapes: 1. How many faces have pairs of parallel edges in: a. A hexagonal pyramid? b. A decagonal (10-sided) based prism? c. A heptagonal based prism? d. Which shape has no face with parallel edges but has parallel edges in the shape? 2. How many faces have perpendicular edges in: a. A pentagonal pyramid b. A hexagonal pyramid c. -

Unit 6 Visualising Solid Shapes(Final)
• 3D shapes/objects are those which do not lie completely in a plane. • 3D objects have different views from different positions. • A solid is a polyhedron if it is made up of only polygonal faces, the faces meet at edges which are line segments and the edges meet at a point called vertex. • Euler’s formula for any polyhedron is, F + V – E = 2 Where F stands for number of faces, V for number of vertices and E for number of edges. • Types of polyhedrons: (a) Convex polyhedron A convex polyhedron is one in which all faces make it convex. e.g. (1) (2) (3) (4) 12/04/18 (1) and (2) are convex polyhedrons whereas (3) and (4) are non convex polyhedron. (b) Regular polyhedra or platonic solids: A polyhedron is regular if its faces are congruent regular polygons and the same number of faces meet at each vertex. For example, a cube is a platonic solid because all six of its faces are congruent squares. There are five such solids– tetrahedron, cube, octahedron, dodecahedron and icosahedron. e.g. • A prism is a polyhedron whose bottom and top faces (known as bases) are congruent polygons and faces known as lateral faces are parallelograms (when the side faces are rectangles, the shape is known as right prism). • A pyramid is a polyhedron whose base is a polygon and lateral faces are triangles. • A map depicts the location of a particular object/place in relation to other objects/places. The front, top and side of a figure are shown. Use centimetre cubes to build the figure. -

Triangulation of Simple 3D Shapes with Well-Centered Tetrahedra
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Illinois Digital Environment for Access to Learning and Scholarship Repository TRIANGULATION OF SIMPLE 3D SHAPES WITH WELL-CENTERED TETRAHEDRA EVAN VANDERZEE, ANIL N. HIRANI, AND DAMRONG GUOY Abstract. A completely well-centered tetrahedral mesh is a triangulation of a three dimensional domain in which every tetrahedron and every triangle contains its circumcenter in its interior. Such meshes have applications in scientific computing and other fields. We show how to triangulate simple domains using completely well-centered tetrahedra. The domains we consider here are space, infinite slab, infinite rectangular prism, cube, and regular tetrahedron. We also demonstrate single tetrahedra with various combinations of the properties of dihedral acuteness, 2-well-centeredness, and 3-well-centeredness. 1. Introduction 3 In this paper we demonstrate well-centered triangulation of simple domains in R . A well- centered simplex is one for which the circumcenter lies in the interior of the simplex [8]. This definition is further refined to that of a k-well-centered simplex which is one whose k-dimensional faces have the well-centeredness property. An n-dimensional simplex which is k-well-centered for all 1 ≤ k ≤ n is called completely well-centered [15]. These properties extend to simplicial complexes, i.e. to meshes. Thus a mesh can be completely well-centered or k-well-centered if all its simplices have that property. For triangles, being well-centered is the same as being acute-angled. But a tetrahedron can be dihedral acute without being 3-well-centered as we show by example in Sect. -

Bicapped Tetrahedral, Trigonal Prismatic, and Octahedral Alternatives in Main and Transition Group Six-Coordination
2484 Bicapped Tetrahedral, Trigonal Prismatic, and Octahedral Alternatives in Main and Transition Group Six-Coordination Roald Hoffmann,*laJames M. Howell,lb and Angelo R. RossilC Contribution from the Departments of Chemistry, Cornell University, Ithaca, New York 14853, Brooklyn College, City University of New York. Brooklyn, New York, 1121 0, and The University of Connecticut, Storrs, Connecticut 06268. Received June 30, 1975 Abstract: We examine theoretically the bicapped tetrahedron and trigonal prism as alternatives to the common octahedron for six-coordinate main and transition group compounds. The pronounced preference of six-coordinate sulfur for an octahe- dral geometry is traced by a molecular orbital analysis to a pair of nonbonding levels, whose higher energy in the nonoctahe- dral geometries is due to the molecular orbital equivalent of a ligand-ligand repulsion. For transition element complexes we draw a correlation diagram for the trigonal twist interrelating octahedral and trigonal prismatic extremes. A possible prefer- ence for the trigonal prism in systems with few d electrons is discussed, as well as a strategy for lowering the energy of the trigonal prism by symmetry-conditioned 7r bonding. The bicapped tetrahedron geometry for transition metal complexes can be stabilized by a substitution pattern ML4D2 where D is a good u donor and M is a d6 metal center. In main and transition group six-coordinate compounds logical, or group theoretical analysis of rearrangement the octahedral geometry predominates. There is, however, a modes or basic permutational sets. However, the solution of growing class of trigonal prismatic complexes and struc- the mathematical problem leaves the question of the physi- tures intermediate between the octahedron and trigonal cal mechanism of a rearrangement still unsolved. -
![[ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated Into This Format from Data Given In](https://docslib.b-cdn.net/cover/6670/entry-polyhedra-authors-oliver-knill-december-2000-source-translated-into-this-format-from-data-given-in-1456670.webp)
[ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated Into This Format from Data Given In
ENTRY POLYHEDRA [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated into this format from data given in http://netlib.bell-labs.com/netlib tetrahedron The [tetrahedron] is a polyhedron with 4 vertices and 4 faces. The dual polyhedron is called tetrahedron. cube The [cube] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. hexahedron The [hexahedron] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. octahedron The [octahedron] is a polyhedron with 6 vertices and 8 faces. The dual polyhedron is called cube. dodecahedron The [dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called icosahedron. icosahedron The [icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called dodecahedron. small stellated dodecahedron The [small stellated dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called great dodecahedron. great dodecahedron The [great dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called small stellated dodecahedron. great stellated dodecahedron The [great stellated dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called great icosahedron. great icosahedron The [great icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called great stellated dodecahedron. truncated tetrahedron The [truncated tetrahedron] is a polyhedron with 12 vertices and 8 faces. The dual polyhedron is called triakis tetrahedron. cuboctahedron The [cuboctahedron] is a polyhedron with 12 vertices and 14 faces. The dual polyhedron is called rhombic dodecahedron. -

Study Guide 3
Study Guide 3 Circles, Central and Inscribed angles 1. How do we define a circle? What is a radius, diameter, chord, secant and tangent? What is a minor and major arc? What is a semi-circle? 2. Circular Geoboard (with 24 pegs): a) Without a protractor, construct the following central angles: 75°, 90°, 135°, 180°, 270°. b) Without a protractor, construct the following inscribed angles: 40°, 90°, 135°. c) Classify all angles you drew in a) and b) . (Using words acute, obtuse, reflex, etc.) 3. Circular Geoboard (with 24 pegs): Find the measures of given central and inscribed angles without using a protractor. (See pg. 259, # 8 a) 4. When is the measure of an inscribed angle equal to 90°? Use this knowledge to find the center of a given circle. Solids Classification, Euler’s Formula You should be familiar with the basic terminology and names: Vertex, Edge, Face; Solid, Polyhedron, Prism, Pyramid, Platonic Solid, Regular Polyhedron, Archimedean Solid, Semiregular Polyhedron, Sphere, Cone, and Cylinder . You don’t have to memorize any definitions – the focus is on understanding, see the examples of possible test questions below. A. Name the solids depicted in the following picture. Be as specific as you can (don’t just state “pyramid”; specify what kind of pyramid it is). Sort out the solids using categories polyhedron , prism , pyramid and platonic solid . (Note: Some do not belong to any category and some may belong to more than one group). B. You should be able to represent relationships between/among different categories of solids in Venn Diagrams (in the class we used a tree diagram to classify solids). -

PLATONIC SOLIDS They Are 5 Shapes Named After the Greek Philosopher Plato
IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 PLATONIC SOLIDS They are 5 shapes named after the Greek philosopher Plato. They have the same congruent regular polygon as each face. Each shape will fit perfectly inside a sphere. Every point will touch the sphere! It is speculated that these 5 shapes are the fundamental building blocks of the physical universe. Plato believed that these 5 shapes where the "atoms" of nature and assigned them to the essential elements of nature: Fire- Tetrahedron Earth- cube Air- octahedron Universe- Icosahedron Water- Dodecahedron 1 IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 Chapter 12 - Solids Polyhedron: a solid that is bounded by polygons, called faces, that enclose a single region of space. Face: is the side of a solid. (a 2- dimensional shape) Edge: is a line segment formed by the intersection of 2 faces. Vertex: a point where 3 or more edges meet. 2 IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 Types of Solids: 3 IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 e. d. 4 IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 Cross section: Is the intersection of the plane and the solid. Imagine that the plane is slicing through a solid. d. e. f. 5 IntGeom12.1.exploringSolids_Prisms.notebook May 08, 2017 Net of a Prism Net: is the 2-dimensional representation of the faces. (imagine that you unfold the polyhedra.) Surface Area: is the sum of the area of the polyhedra's faces. ** The Surface Area is equal to the Area of the polyhedra's net ** Lateral Area: is the sum of the areas of its lateral faces. -

Paper Models of Polyhedra
Paper Models of Polyhedra Gijs Korthals Altes Polyhedra are beautiful 3-D geometrical figures that have fascinated philosophers, mathematicians and artists for millennia Copyrights © 1998-2001 Gijs.Korthals Altes All rights reserved . It's permitted to make copies for non-commercial purposes only email: [email protected] Paper Models of Polyhedra Platonic Solids Dodecahedron Cube and Tetrahedron Octahedron Icosahedron Archimedean Solids Cuboctahedron Icosidodecahedron Truncated Tetrahedron Truncated Octahedron Truncated Cube Truncated Icosahedron (soccer ball) Truncated dodecahedron Rhombicuboctahedron Truncated Cuboctahedron Rhombicosidodecahedron Truncated Icosidodecahedron Snub Cube Snub Dodecahedron Kepler-Poinsot Polyhedra Great Stellated Dodecahedron Small Stellated Dodecahedron Great Icosahedron Great Dodecahedron Other Uniform Polyhedra Tetrahemihexahedron Octahemioctahedron Cubohemioctahedron Small Rhombihexahedron Small Rhombidodecahedron S mall Dodecahemiododecahedron Small Ditrigonal Icosidodecahedron Great Dodecahedron Compounds Stella Octangula Compound of Cube and Octahedron Compound of Dodecahedron and Icosahedron Compound of Two Cubes Compound of Three Cubes Compound of Five Cubes Compound of Five Octahedra Compound of Five Tetrahedra Compound of Truncated Icosahedron and Pentakisdodecahedron Other Polyhedra Pentagonal Hexecontahedron Pentagonalconsitetrahedron Pyramid Pentagonal Pyramid Decahedron Rhombic Dodecahedron Great Rhombihexacron Pentagonal Dipyramid Pentakisdodecahedron Small Triakisoctahedron Small Triambic -
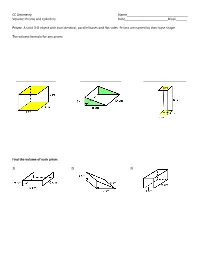
CC Geometry Name______Volume: Prisms and Cylinders Date______Block______
CC Geometry Name__________________________________ Volume: Prisms and Cylinders Date________________________Block______ Prism: A solid 3-D object with two identical, parallel bases and flat sides. Prisms are named by their base shape. The volume formula for any prism: ______________________ _______________________ ________________________ Find the volume of each prism. 1) 2) 3) 4) The cube and the rectangular prism below have the same volume. Find the height of the rectangular prism to the nearest tenth. Cylinder: A 3-D object that has circles as the bases. Volume of a cylinder: Find the volume for each cylinder to the nearest tenth. 1) 2) 3) Find the volume of each cylinder in terms of 흅. 4) 5) Word Problems 1) A cylinder has a volume of 1402.4 cm3. If the radius of the base is 6cm, find the height to the nearest tenth. 2) The circumference of the base of a cylinder is 20.1 inches. If the volume of the cylinder is 305.6 in3, find the radius to the nearest tenth. 3) A solid wooden prism has a rectangular base with sides 5 inches, 7 inches and a height of 5 inches. A hole, in the shape of a cylinder with a radius of 1 inch, is drilled through the entire length of the prism. Find the volume remaining in the prism to the nearest cubic inch. 5in 5in 7in 4) A barrel of fuel oil is a right circular cylinder where the inside measurements of the barrel are a diameter of 22.5 inches and a height of 33.5 inches. There are 231 cubic inches in a liquid gallon.