DOCSLIB.ORG

The Mean Value Theorem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Mean Value Theorem The Mean Value Theorem The mean value theorem is an extremely useful result, although unfortunately the power of the mean value theorem does not shine through in an introductory calculus course. This is because the main application of the mean value theorem is proving further results, but our focus is not on proving the theorems of calculus. Motivated students may consider studying real analysis, in which the focus of study is proving and understanding the propositions of calculus. Without further ado, we will consider the mean value theorem. Theorem: The Mean Value Theorem If f is continuous on the closed interval [a, b], and differentiable on the interval’s interior (a, b), then there exists at least one point c ∈ (a, b) at which f(b) − f(a) = f 0(c) b − a Verbally, the mean value theorem states: for a continuous and differentiable function f on an interval, we can find a point inside the interval at which the instantaneous rate of change of f is equal to the average rate of change of f over that interval. In other words, if we draw the secant line between the points (a, f(a)) and (b, f(b)), we can find a point c ∈ (a, b) so that the slope of the tangent line at c, f 0(c), is the same as the slope of the secant line through the endpoints of the interval. If we think of the average rate of change over an interval as the mean rate of change, then the name of this theorem makes sense. It is important to emphasize that the mean value theorem does not apply for functions which are not continuous on the closed interval [a, b], or not differentiable on the open interval (a, b). Consider the function 0 x = 0 f(x) = 0.5 0 < x < 1 1 x = 1 If we look at the average rate of change on [0, 1] we find f(1) − f(0) = 1 1 − 0 and we find the secant line through the points (0, f(0)) and (1, f(1)) is just the line of slope one that passes through the origin. What about the derivative of this function? It turns out f 0(x) does not exist at x = 0 and x = 1, because the function is not continuous at those points. However, for 0 < x < 1 the function is continuous, and just a constant, so the derivative f 0(x) = 0. It can be seen that there are no points in this interval for which the slope of the tangent line is 1, because for all points in (0, 1) the tangent line is horizontal, having slope 0. Here the mean value did not apply because we had a function that was not continuous on [0, 1], even though it was differentiable on (0, 1). It is noteworthy that we could still apply the mean value theorem on any closed interval contained in (0, 1), and it would tell us that somewhere in the interval the slope of the tangent line is 0 (which is not particularly useful, as we already know that the tangent line is 0 everywhere in the interval). Now let us consider a function that is continuous on a closed interval, but not differentiable within the open interval. Let us consider f(x) = |x| on the interval [−1, 1]. If we look at the average rate of change over the interval we find f(1) − f(−1) 0 = = 0 1 − (−1) 2 Yet there are no points c ∈ (−1, 1) such that f 0(c) = 0. For x < 0 we have f 0(x) = −1 and for x > 0 we have f 0(x) = 1 (of course f 0(0) does not exist). If the function |x| were differentiable at x = 0, then in a sense, we would have to have f 0(0) = 0, as this would be the point where the derivative would change from negative to positive. However, in this case we don’t have any points with a zero derivative, and because the derivative is discontinous at x = 0, it is possible for us to jump from a positive to negative derivative. We gain further information from the mean value theorem in the following two corollaries (a corollary is a minor result that follows almost immediately from major theorem): 1. If f 0(x) = 0 for all x in an open interval (a, b), then f(x) = C for all x ∈ (a, b), where C is a constant. 2. If f 0(x) = g0(x) for all x in an open interval (a, b), then there exists some constant C so that f(x) = g(x) + C for some x ∈ (a, b). Both of these results are things that we already knew intuitively, but follow rigorously from the mean value theorem. To move from the first of these results to the second, we consider the function (f − g)(x). For this function, (f − g)0(x) = f 0(x) − g0(x) = 0 on the interval (a, b), so (f − g)(x) = C for some constant, and thus f(x) = g(x) + C. If we apply the mean value theorem on an interval for which f(a) = f(b), it follows that there exists a point c ∈ (a, b) so that f(b) − f(a) f 0(c) = = 0 b − a This means that if we have any two points a and b at which our function of interest crosses the x-axis, we can find a point in the interval which is a critical point (at which we could look for a local extremum). This result is called Rolle’s theorem, and is used in the proof of the mean value theorem, but really ought to be called Rolle’s lemma, because a lemma is a minor result that is used in the proof of a major result, but is not thought of as an extremely important result of mathematics in its own right. If we think about the function x3 f(x) = − 3x 3 which is 0 at −3, 0, 3, then we know it has a critical point somewhere in the intervals (−3, 0) and (0, 3). Thus, we know it has at least two critical points, but it could have more. We can also use the mean value theorem in the classification of critical points. Going back to the above function x3 f(x) = − 3x 3 defined on the interval [−3, 3], we find that f 0(x) = x2 − 3 √ √ which is 0 when x = ± 3, meaning that ± 3 are critical points. The next step is for us to evaluate the value√ of the√ function√ at each√ of the critical points and endpoints, yielding f(−3) = 0, f(− 3) = 2 3, f( 3) = −2 3, and f(3) = 0. Normally we think of these points as partitioning our larger interval into subintervals, over which we want to consider the sign of the derivative. Since the sign of the derivative cannot change over these intervals, knowing the sign of the derivative at some point in the interval tells us the sign of the derivative over the entire subinterval.√ If we apply the mean value theorem to√ the endpoints of one of these subintervals, say [ 3, 3], we find that there exists some c ∈ ( 3, 3) so that √ √ f(3) − f( 3) 0 − (−2 3) f 0(c) = √ = √ > 0 3 − 3 3 − 3 which means that the derivative must be positive, so the function is increasing, over the interior of the entire subinterval. Note that the denominator will always be positive when we apply the mean value theorem, and since we only care about the sign of the derivative, we simply need to determine the relative magnitude of the√ endpoints√ to see√ if the derivative√ will be positive or negative. Doing so we can see that f( 3)√ =√−2 3 < 2 3 = f(−√ 3) which implies the derivative is negative on the subinterval (− 3, 3),√ and finally f(− 3) > f√(3) implies that the derivative is√ positive over the subinterval (−3, − 3). It follows that f(− 3) is a local maximum, and f( 3) is a local minimum. Finally, there is another application of the mean value theorem that proves to be extremely useful in many cases. The mean value theorem allows us to transform a bounded derivative into a bound for a function defined on an interval. Let’s suppose that we have a function f which is continuous on the interval [a, b], differentiable on (a, b), and that |f 0(x)| < B for all x ∈ (a, b) (this means that the derivative of f is bounded). This bound on the derivative tells us intuitively that the function can only change so fast. In fact, the maximum rate at which it can change is B. Intuitively, if the function can only change so fast, then it should not be able to become too much larger or smaller than f(a) (or f(b) for that matter) if we don’t move too far from x = a. Let us consider a point x ∈ (a, b). Applying the mean value theorem on the interval [a, x] we find f(x) − f(a) = f 0(c) x − a for some c ∈ (a, x). Rearranging terms it follows f(x) = f 0(c)(x − a) + f(a) although this looks like the equation for a line, remember that x is a fixed value, and for any value of x, we might actually find a different value for c. Normally we would find f 0(c) using information about f(x) and f(a), but here we want to gain some information about f(x).
Load more

Recommended publications
  • The Directional Derivative the Derivative of a Real Valued Function (Scalar field) with Respect to a Vector
    Math 253 The Directional Derivative The derivative of a real valued function (scalar field) with respect to a vector. f(x + h) f(x) What is the vector space analog to the usual derivative in one variable? f 0(x) = lim − ? h 0 h ! x -2 0 2 5 Suppose f is a real valued function (a mapping f : Rn R). ! (e.g. f(x; y) = x2 y2). − 0 Unlike the case with plane figures, functions grow in a variety of z ways at each point on a surface (or n{dimensional structure). We'll be interested in examining the way (f) changes as we move -5 from a point X~ to a nearby point in a particular direction. -2 0 y 2 Figure 1: f(x; y) = x2 y2 − The Directional Derivative x -2 0 2 5 We'll be interested in examining the way (f) changes as we move ~ in a particular direction 0 from a point X to a nearby point . z -5 -2 0 y 2 Figure 2: f(x; y) = x2 y2 − y If we give the direction by using a second vector, say ~u, then for →u X→ + h any real number h, the vector X~ + h~u represents a change in X→ position from X~ along a line through X~ parallel to ~u. →u →u h x Figure 3: Change in position along line parallel to ~u The Directional Derivative x -2 0 2 5 We'll be interested in examining the way (f) changes as we move ~ in a particular direction 0 from a point X to a nearby point .
    [Show full text]
  • Cauchy Integral Theorem
    Cauchy’s Theorems I Ang M.S. Augustin-Louis Cauchy October 26, 2012 1789 – 1857 References Murray R. Spiegel Complex V ariables with introduction to conformal mapping and its applications Dennis G. Zill , P. D. Shanahan A F irst Course in Complex Analysis with Applications J. H. Mathews , R. W. Howell Complex Analysis F or Mathematics and Engineerng 1 Summary • Cauchy Integral Theorem Let f be analytic in a simply connected domain D. If C is a simple closed contour that lies in D , and there is no singular point inside the contour, then ˆ f (z) dz = 0 C • Cauchy Integral Formula (For simple pole) If there is a singular point z0 inside the contour, then ˛ f(z) dz = 2πj f(z0) z − z0 • Generalized Cauchy Integral Formula (For pole with any order) ˛ f(z) 2πj (n−1) n dz = f (z0) (z − z0) (n − 1)! • Cauchy Inequality M · n! f (n)(z ) ≤ 0 rn • Gauss Mean Value Theorem ˆ 2π ( ) 1 jθ f(z0) = f z0 + re dθ 2π 0 1 2 Related Mathematics Review 2.1 Stoke’s Theorem ¨ ˛ r × F¯ · dS = F¯ · dr Σ @Σ (The proof is skipped) ¯ Consider F = (FX ;FY ;FZ ) 0 1 x^ y^ z^ B @ @ @ C r × F¯ = det B C @ @x @y @z A FX FY FZ Let FZ = 0 0 1 x^ y^ z^ B @ @ @ C r × F¯ = det B C @ @x @y @z A FX FY 0 dS =ndS ^ , for dS = dxdy , n^ =z ^ . By z^ · z^ = 1 , consider z^ component only for r × F¯ 0 1 x^ y^ z^ ( ) B @ @ @ C @F @F r × F¯ = det B C = Y − X z^ @ @x @y @z A @x @y FX FY 0 i.e.
    [Show full text]
  • Infinitesimal and Tangent to Polylogarithmic Complexes For
    AIMS Mathematics, 4(4): 1248–1257. DOI:10.3934/math.2019.4.1248 Received: 11 June 2019 Accepted: 11 August 2019 http://www.aimspress.com/journal/Math Published: 02 September 2019 Research article Infinitesimal and tangent to polylogarithmic complexes for higher weight Raziuddin Siddiqui* Department of Mathematical Sciences, Institute of Business Administration, Karachi, Pakistan * Correspondence: Email: [email protected]; Tel: +92-213-810-4700 Abstract: Motivic and polylogarithmic complexes have deep connections with K-theory. This article gives morphisms (different from Goncharov’s generalized maps) between |-vector spaces of Cathelineau’s infinitesimal complex for weight n. Our morphisms guarantee that the sequence of infinitesimal polylogs is a complex. We are also introducing a variant of Cathelineau’s complex with the derivation map for higher weight n and suggesting the definition of tangent group TBn(|). These tangent groups develop the tangent to Goncharov’s complex for weight n. Keywords: polylogarithm; infinitesimal complex; five term relation; tangent complex Mathematics Subject Classification: 11G55, 19D, 18G 1. Introduction The classical polylogarithms represented by Lin are one valued functions on a complex plane (see [11]). They are called generalization of natural logarithms, which can be represented by an infinite series (power series): X1 zk Li (z) = = − ln(1 − z) 1 k k=1 X1 zk Li (z) = 2 k2 k=1 : : X1 zk Li (z) = for z 2 ¼; jzj < 1 n kn k=1 The other versions of polylogarithms are Infinitesimal (see [8]) and Tangential (see [9]). We will discuss group theoretic form of infinitesimal and tangential polylogarithms in x 2.3, 2.4 and 2.5 below.
    [Show full text]
  • 1 Mean Value Theorem 1 1.1 Applications of the Mean Value Theorem
    Seunghee Ye Ma 8: Week 5 Oct 28 Week 5 Summary In Section 1, we go over the Mean Value Theorem and its applications. In Section 2, we will recap what we have covered so far this term. Topics Page 1 Mean Value Theorem 1 1.1 Applications of the Mean Value Theorem . .1 2 Midterm Review 5 2.1 Proof Techniques . .5 2.2 Sequences . .6 2.3 Series . .7 2.4 Continuity and Differentiability of Functions . .9 1 Mean Value Theorem The Mean Value Theorem is the following result: Theorem 1.1 (Mean Value Theorem). Let f be a continuous function on [a; b], which is differentiable on (a; b). Then, there exists some value c 2 (a; b) such that f(b) − f(a) f 0(c) = b − a Intuitively, the Mean Value Theorem is quite trivial. Say we want to drive to San Francisco, which is 380 miles from Caltech according to Google Map. If we start driving at 8am and arrive at 12pm, we know that we were driving over the speed limit at least once during the drive. This is exactly what the Mean Value Theorem tells us. Since the distance travelled is a continuous function of time, we know that there is a point in time when our speed was ≥ 380=4 >>> speed limit. As we can see from this example, the Mean Value Theorem is usually not a tough theorem to understand. The tricky thing is realizing when you should try to use it. Roughly speaking, we use the Mean Value Theorem when we want to turn the information about a function into information about its derivative, or vice-versa.
    [Show full text]
  • Circles Project
    Circles Project C. Sormani, MTTI, Lehman College, CUNY MAT631, Fall 2009, Project X BACKGROUND: General Axioms, Half planes, Isosceles Triangles, Perpendicular Lines, Con- gruent Triangles, Parallel Postulate and Similar Triangles. DEFN: A circle of radius R about a point P in a plane is the collection of all points, X, in the plane such that the distance from X to P is R. That is, C(P; R) = fX : d(X; P ) = Rg: Note that a circle is a well defined notion in any metric space. We say P is the center and R is the radius. If d(P; Q) < R then we say Q is an interior point of the circle, and if d(P; Q) > R then Q is an exterior point of the circle. DEFN: The diameter of a circle C(P; R) is a line segment AB such that A; B 2 C(P; R) and the center P 2 AB. The length AB is also called the diameter. THEOREM: The diameter of a circle C(P; R) has length 2R. PROOF: Complete this proof using the definition of a line segment and the betweenness axioms. DEFN: If A; B 2 C(P; R) but P2 = AB then AB is called a chord. THEOREM: A chord of a circle C(P; R) has length < 2R unless it is the diameter. PROOF: Complete this proof using axioms and the above theorem. DEFN: A line L is said to be a tangent line to a circle, if L \ C(P; R) is a single point, Q. The point Q is called the point of contact and L is said to be tangent to the circle at Q.
    [Show full text]
  • 2. the Tangent Line
    2. The Tangent Line The tangent line to a circle at a point P on its circumference is the line perpendicular to the radius of the circle at P. In Figure 1, The line T is the tangent line which is Tangent Line perpendicular to the radius of the circle at the point P. T Figure 1: A Tangent Line to a Circle While the tangent line to a circle has the property that it is perpendicular to the radius at the point of tangency, it is not this property which generalizes to other curves. We shall make an observation about the tangent line to the circle which is carried over to other curves, and may be used as its defining property. Let us look at a specific example. Let the equation of the circle in Figure 1 be x22 + y = 25. We may easily determine the equation of the tangent line to this circle at the point P(3,4). First, we observe that the radius is a segment of the line passing through the origin (0, 0) and P(3,4), and its equation is (why?). Since the tangent line is perpendicular to this line, its slope is -3/4 and passes through P(3, 4), using the point-slope formula, its equation is found to be Let us compute y-values on both the tangent line and the circle for x-values near the point P(3, 4). Note that near P, we can solve for the y-value on the upper half of the circle which is found to be When x = 3.01, we find the y-value on the tangent line is y = -3/4(3.01) + 25/4 = 3.9925, while the corresponding value on the circle is (Note that the tangent line lie above the circle, so its y-value was expected to be a larger.) In Table 1, we indicate other corresponding values as we vary x near P.
    [Show full text]
  • MATH 25B Professor: Bena Tshishiku Michele Tienni Lowell House
    MATH 25B Professor: Bena Tshishiku Michele Tienni Lowell House Cambridge, MA 02138 [email protected] Please note that these notes are not official and they are not to be considered as a sub- stitute for your notes. Specifically, you should not cite these notes in any of the work submitted for the class (problem sets, exams). The author does not guarantee the accu- racy of the content of this document. If you find a typo (which will probably happen) feel free to email me. Contents 1. January 225 1.1. Functions5 1.2. Limits6 2. January 247 2.1. Theorems about limits7 2.2. Continuity8 3. January 26 10 3.1. Continuity theorems 10 4. January 29 – Notes by Kim 12 4.1. Least Upper Bound property (the secret sauce of R) 12 4.2. Proof of the intermediate value theorem 13 4.3. Proof of the boundedness theorem 13 5. January 31 – Notes by Natalia 14 5.1. Generalizing the boundedness theorem 14 5.2. Subsets of Rn 14 5.3. Compactness 15 6. February 2 16 6.1. Onion ring theorem 16 6.2. Proof of Theorem 6.5 17 6.3. Compactness of closed rectangles 17 6.4. Further applications of compactness 17 7. February 5 19 7.1. Derivatives 19 7.2. Computing derivatives 20 8. February 7 22 8.1. Chain rule 22 Date: April 25, 2018. 1 8.2. Meaning of f 0 23 9. February 9 25 9.1. Polynomial approximation 25 9.2. Derivative magic wands 26 9.3. Taylor’s Theorem 27 9.4.
    [Show full text]
  • Continuous Functions, Smooth Functions and the Derivative C 2012 Yonatan Katznelson
    ucsc supplementary notes ams/econ 11a Continuous Functions, Smooth Functions and the Derivative c 2012 Yonatan Katznelson 1. Continuous functions One of the things that economists like to do with mathematical models is to extrapolate the general behavior of an economic system, e.g., forecast future trends, from theoretical assumptions about the variables and functional relations involved. In other words, they would like to be able to tell what's going to happen next, based on what just happened; they would like to be able to make long term predictions; and they would like to be able to locate the extreme values of the functions they are studying, to name a few popular applications. Because of this, it is convenient to work with continuous functions. Definition 1. (i) The function y = f(x) is continuous at the point x0 if f(x0) is defined and (1.1) lim f(x) = f(x0): x!x0 (ii) The function f(x) is continuous in the interval (a; b) = fxja < x < bg, if f(x) is continuous at every point in that interval. Less formally, a function is continuous in the interval (a; b) if the graph of that function is a continuous (i.e., unbroken) line over that interval. Continuous functions are preferable to discontinuous functions for modeling economic behavior because continuous functions are more predictable. Imagine a function modeling the price of a stock over time. If that function were discontinuous at the point t0, then it would be impossible to use our knowledge of the function up to t0 to predict what will happen to the price of the stock after time t0.
    [Show full text]
  • The Mean Value Theorem) – Be Able to Precisely State the Mean Value Theorem and Rolle’S Theorem
    Math 220 { Test 3 Information The test will be given during your lecture period on Wednesday (April 27, 2016). No books, notes, scratch paper, calculators or other electronic devices are allowed. Bring a Student ID. It may be helpful to look at • http://www.math.illinois.edu/~murphyrf/teaching/M220-S2016/ { Volumes worksheet, quizzes 8, 9, 10, 11 and 12, and Daily Assignments for a summary of each lecture • https://compass2g.illinois.edu/ { Homework solutions • http://www.math.illinois.edu/~murphyrf/teaching/M220/ { Tests and quizzes in my previous courses • Section 3.10 (Linear Approximation and Differentials) { Be able to use a tangent line (or differentials) in order to approximate the value of a function near the point of tangency. • Section 4.2 (The Mean Value Theorem) { Be able to precisely state The Mean Value Theorem and Rolle's Theorem. { Be able to decide when functions satisfy the conditions of these theorems. If a function does satisfy the conditions, then be able to find the value of c guaranteed by the theorems. { Be able to use The Mean Value Theorem, Rolle's Theorem, or earlier important the- orems such as The Intermediate Value Theorem to prove some other fact. In the homework these often involved roots, solutions, x-intercepts, or intersection points. • Section 4.8 (Newton's Method) { Understand the graphical basis for Newton's Method (that is, use the point where the tangent line crosses the x-axis as your next estimate for a root of a function). { Be able to apply Newton's Method to approximate roots, solutions, x-intercepts, or intersection points.
    [Show full text]
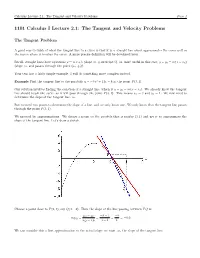
  • 1101 Calculus I Lecture 2.1: the Tangent and Velocity Problems
    Calculus Lecture 2.1: The Tangent and Velocity Problems Page 1 1101 Calculus I Lecture 2.1: The Tangent and Velocity Problems The Tangent Problem A good way to think of what the tangent line to a curve is that it is a straight line which approximates the curve well in the region where it touches the curve. A more precise definition will be developed later. Recall, straight lines have equations y = mx + b (slope m, y-intercept b), or, more useful in this case, y − y0 = m(x − x0) (slope m, and passes through the point (x0, y0)). Your text has a fairly simple example. I will do something more complex instead. Example Find the tangent line to the parabola y = −3x2 + 12x − 8 at the point P (3, 1). Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). We already know the tangent line should touch the curve, so it will pass through the point P (3, 1). This means x0 = 3 and y0 = 1. We now need to determine the slope of the tangent line, m. But we need two points to determine the slope of a line, and we only know one. We only know that the tangent line passes through the point P (3, 1). We proceed by approximations. We choose a point on the parabola that is nearby (3,1) and use it to approximate the slope of the tangent line. Let’s draw a sketch. Choose a point close to P (3, 1), say Q(4, −8).
    [Show full text]
  • A Brief Summary of Math 125 the Derivative of a Function F Is Another
    A Brief Summary of Math 125 The derivative of a function f is another function f 0 defined by f(v) − f(x) f(x + h) − f(x) f 0(x) = lim or (equivalently) f 0(x) = lim v!x v − x h!0 h for each value of x in the domain of f for which the limit exists. The number f 0(c) represents the slope of the graph y = f(x) at the point (c; f(c)). It also represents the rate of change of y with respect to x when x is near c. This interpretation of the derivative leads to applications that involve related rates, that is, related quantities that change with time. An equation for the tangent line to the curve y = f(x) when x = c is y − f(c) = f 0(c)(x − c). The normal line to the curve is the line that is perpendicular to the tangent line. Using the definition of the derivative, it is possible to establish the following derivative formulas. Other useful techniques involve implicit differentiation and logarithmic differentiation. d d d 1 xr = rxr−1; r 6= 0 sin x = cos x arcsin x = p dx dx dx 1 − x2 d 1 d d 1 ln jxj = cos x = − sin x arccos x = −p dx x dx dx 1 − x2 d d d 1 ex = ex tan x = sec2 x arctan x = dx dx dx 1 + x2 d 1 d d 1 log jxj = ; a > 0 cot x = − csc2 x arccot x = − dx a (ln a)x dx dx 1 + x2 d d d 1 ax = (ln a) ax; a > 0 sec x = sec x tan x arcsec x = p dx dx dx jxj x2 − 1 d d 1 csc x = − csc x cot x arccsc x = − p dx dx jxj x2 − 1 d product rule: F (x)G(x) = F (x)G0(x) + G(x)F 0(x) dx d F (x) G(x)F 0(x) − F (x)G0(x) d quotient rule: = chain rule: F G(x) = F 0G(x) G0(x) dx G(x) (G(x))2 dx Mean Value Theorem: If f is continuous on [a; b] and differentiable on (a; b), then there exists a number f(b) − f(a) c in (a; b) such that f 0(c) = .
    [Show full text]
  • Secant Lines TEACHER NOTES
    TEACHER NOTES Secant Lines About the Lesson In this activity, students will observe the slopes of the secant and tangent line as a point on the function approaches the point of tangency. As a result, students will: • Determine the average rate of change for an interval. • Determine the average rate of change on a closed interval. • Approximate the instantaneous rate of change using the slope of the secant line. Tech Tips: Vocabulary • This activity includes screen • secant line captures taken from the TI-84 • tangent line Plus CE. It is also appropriate for use with the rest of the TI-84 Teacher Preparation and Notes Plus family. Slight variations to • Students are introduced to many initial calculus concepts in this these directions may be activity. Students develop the concept that the slope of the required if using other calculator tangent line representing the instantaneous rate of change of a models. function at a given value of x and that the instantaneous rate of • Watch for additional Tech Tips change of a function can be estimated by the slope of the secant throughout the activity for the line. This estimation gets better the closer point gets to point of specific technology you are tangency. using. (Note: This is only true if Y1(x) is differentiable at point P.) • Access free tutorials at http://education.ti.com/calculato Activity Materials rs/pd/US/Online- • Compatible TI Technologies: Learning/Tutorials • Any required calculator files can TI-84 Plus* be distributed to students via TI-84 Plus Silver Edition* handheld-to-handheld transfer. TI-84 Plus C Silver Edition TI-84 Plus CE Lesson Files: * with the latest operating system (2.55MP) featuring MathPrint TM functionality.
    [Show full text]