DOCSLIB.ORG

Part IV Elasticity and Thermodynamics of Reversible Processes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Part IV Elasticity and Thermodynamics of Reversible Processes Part IV Elasticity and Thermodynamics of Reversible Processes 175 Chapter 5 Elasticity: An Energy Approach Matter deforms when subjected to stresses. The English experimental physi- cist and inventor Robert Hooke (1635—1703), a contemporary of Isaac New- ton, rst stated formally this observation as an empirical relation, ‘ut tensio, sic vis’, which translates into our language as ‘extension is directly propor- tional to force’. In Engineering Mechanics, this observation translates into the theory of linear elasticity. Elasticity describes reversible material be- havior, and the notion of reversibility is a hallmark of another engineering science discipline: Thermodynamics. Thermodynamics is the study of en- ergy and energy transformations. Energy, which exists in many forms, such as heat, light, chemical energy, and electrical energy, is the ability to bring about change or to do work. Hence, an elastic, ie. reversible, behavior is readily recognized to be one where the energy provided to a material or structural system from the outside in form of work by forces and stresses, is stored as internal energy, which can be completely recovered at any time. Thermodynamics, therefore, provides a means to connect an observation to a fundamental physics law. The focus of this Chapter is to employ the laws of thermodynamics as a backbone for the engineering investigation of linear elastic behavior of materials and structures. 176 5.1. 1-D ENERGY APPROACH 177 0.4 d F0.35 0.3 0.25 0.2 KS 0.15 (x) 0.1 0.05 K x S 0 1 0 0.1 0.2x 0.3 0.4 0.5 F d Figure 5.1: Elasticity: 1-D Thought Model of Elasticity (left), and force— displacement curve with free energy (right). 5.1 1-D Energy Approach The 1-D spring system subjected to a force ononesideisthesimplest representation of an elastic behavior (Fig. 5.1). While equilibrium tells us that the externally supplied force is equal to the force in the spring, that is, = , Hooke’s observational law links to the extension at the point of load application through the proportionality constant (of dimension 1 2 []= [ ]= ): = = (5.1) Note that the elastic behavior of the spring may also be non-linear (Fig. 5.1). However, in all what follows we will restrict ourselves to linear elasticity. Let us now take another route to the problem, by evoking the First Law and the Second Law of Thermodynamics. 5.1.1 The First Law The First Law of Thermodynamics states that energy can be changed from one form to another, but that it cannot be created or destroyed. Energy is conserved. This is expressed by the internal energy U of a system (of dimension [U]=22). Specically the First Law informs us that the 178 CHAPTER 5. ELASTICITY: AN ENERGY APPROACH change in internal energy U of a system is due to work W and heat Q provided from the outside. Formally we write: U W Q (5.2) = + where we employ the symbol ‘ ( )’ to specify that the rate is not necessarily the time derivative of a function . For instance, the work rate W is generally not the total time derivative of the work W, ie. W =6 W .For instance, in the case of our 1-D spring system, the total work is W = , and the time derivative is W = + . In contrast, the work rate W is what the force realizes along the velocity = 0 at the point of load application, that is, W = . 5.1.2 The Second Law The Second Law of Thermodynamics species the direction of spontaneous change of energy, which is expressed by another physics quantity, the internal entropy S (of dimension [S]=221). The entropy is a measure of the quality of the energy. Specically, the Second Law informs us that the change of the internal entropy is always greater or equal to the entropy supplied to a system in heat form; that is: S Q (5.3) 0 where 0 0 stands for the absolute temperature, which is assumed to be constant in what follows. The dierence between the left and the right hand side is recognized as the fraction of entropy which is produced internally in aspontaneous(ie. uncontrolled) fashion, and which manifests itself as an internal heat source, D S Q = 0 0 (5.4) This internal heat source is called dissipation. More specically, if we substi- tute the First Law (5.2) into (5.4), we obtain: D W U S = ( 0 ) 0 (5.5) In this form, the Second Law appears as a balance law between the external work rate W and some form of recoverable energy (U 0S). This energy 5.1. 1-D ENERGY APPROACH 179 is called the free energy or Helmholtz Energy, which we denote by ,and which expresses the maximum internal capacity of a system to do work: =U 0S (5.6) By denition, an elastic behavior is one where the entire work rate supplied from the outside is stored as recoverable energy; that is: D W (5.7) Elastic: = =0 Hence, since W is known, it suces to determine the expression of the free energy of the spring. In the case of our 1-D spring system, the free energy is recognized to be the area below the curve (Fig. 5.1); thus in the 1 2 case of the linear behavior =( )= 2 . Use in (5.7) yields: μ ¶ =0 (5.8) Since this relation must hold for any rate we come to the same result as (5.1): ; = = (5.9) In contrast to (5.1) which was based on equilibrium and Hooke’s observational law, we here operate with energy states described by a state variable; here . If we add now one additional equilibrium condition to (5.9) we have instead of (5.1): ! = = = (5.10) The partial derivative of w.r.t. is called state equation, and species the constitutive law of the spring force in equilibrium with the external force . Finally, if the spring stiness is constant, we speak about linear elas- ticity. Inreturnif () depends on ,weneedtodealwithanon linear elasticity problem. On the other hand, it does not need much imagination to gure out that the spring stiness cannotbenegative,sinceitwould make not much sense that the spring extension ,inresponsetotheload , takes o in the opposite direction of the applied force. Behind this ob- servation, however, hides an important property of the free energy function 180 CHAPTER 5. ELASTICITY: AN ENERGY APPROACH x L 123 x z P 0 P Figure 5.2: 1-D Elasticity Example: Three-Truss System =(). In fact, the non-negativity of the spring constant is ensured provided that () is a convex function of its arguments; that is: 2 = 2 0 (5.11) We will see later that this convexity property is of critical importance for solving elasticity problems. 5.1.3 Example: Three-Truss System By way of example, consider the truss system displayed in gure 5.2. The structure is composed of three bars of same length held on the top and connected on the other side to a rigid beam device which is subjected to a load at midspan between two trusses. In a rst approach, such a truss system can be considered as a discrete system, in which each bar represents a spring of stiness . We want to evaluate the forces in the trusses (ie. the spring forces) and evaluate the displacement 0 at the point of load application. Ad hoc Approach To refresh our memory, let us start with equilibrium. Elementary force equilibrium and moment equilibrium (around the point of load application) yields: 1 + 2 + 3 = (5.12a) 31 + 2 3 =0 (5.12b) 5.1. 1-D ENERGY APPROACH 181 We readily recognize that the structure is statically indeterminate of degree 1; that is, there are only two equilibrium relations for the three unknowns, 12 and 3. Let us now introduce a linear elastic constitutive law for each truss of the form: = (5.13) where stands for the elongation of bar =1 3. We now need to ensure the kinematical compatibility between the bar elongations and the constraints on both the top (where the bars are xed) and the bottom where each bar is con- strained by the displacement of the rigid bars at the nodes. Compatibility requires: 1 = 1 (5.14a) 2 2 = = + ( ) (5.14b) 2 1 3 0 1 4 3 = = + ( ) (5.14c) 3 1 3 0 1 While there are apriorithree displacement unknowns in the problem, the geometrical compatibility allows us to reduce these unknowns to two. We here choose 1 and 0, the rst being the displacement of node 1 (Fig. 5.2), the second the displacement at the point of load application. Substitution of the constitutive law (5.13) and the geometrical compatibility conditions (5.14) in the equilibrium relations (5.12) now yields a system of two equations for the two unknowns: μ ( 1 +2 0¶)= (5.15a) 11 2 =0 (5.15b) 3 1 3 0 11 The linear elastic problem then is readily solved: 0 = 24 and 1 = 1 12 . The truss forces are given by: 7 1 = ; 2 = ; 3 = (5.16) 12 3 12 The problem nicely shows that the use of a constitutive law and geometrical compatibility conditions allows one to obtain a unique solution for a stati- cally indeterminate structure. In this approach, we start with equilibrium, substitute for forces a constitutive law that links forces to displacements, and nally ensure that the displacements are geometrically compatible. 182 CHAPTER 5. ELASTICITY: AN ENERGY APPROACH Energy Approach Let us now take the alternative energy route to the problem. Instead of equilibrium, we start out with the external work rate of the applied force : W = 0 (5.17) According to the Thermodynamics of reversible processes expressed by (5.7), this external work rate is equal to the change in free energy of the system.
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • The Conformations of Cycloalkanes
    The Conformations of Cycloalkanes Ring-containing structures are a common occurrence in organic chemistry. We must, therefore spend some time studying the special characteristics of the parent cycloalkanes. Cyclical connectivity imposes constraints on the range of motion that the atoms in rings can undergo. Cyclic molecules are thus more rigid than linear or branched alkanes because cyclic structures have fewer internal degrees of freedom (that is, the motion of one atom greatly influences the motion of the others when they are connected in a ring). In this lesson we will examine structures of the common ring structures found in organic chemistry. The first four cycloalkanes are shown below. cyclopropane cyclobutane cyclopentane cyclohexane The amount of energy stored in a strained ring is estimated by comparing the experimental heat of formation to the calculated heat of formation. The calculated heat of formation is based on the notion that, in the absence of strain, each –CH2– group contributes equally to the heat of formation, in line with the behavior found for the acyclic alkanes (i.e., open chains). Thus, the calculated heat of formation varies linearly with the number of carbon atoms in the ring. Except for the 6-membered ring, the experimental values are found to have a more positive heat of formation than the calculated value owning to ring strain. The plots of calculated and experimental enthalpies of formation and their difference (i.e., ring strain) are seen in the Figure. The 3-membered ring has about 27 kcal/mol of strain. It can be seen that the 6-membered ring possesses almost no ring strain.
    [Show full text]
  • Comparing Models for Measuring Ring Strain of Common Cycloalkanes
    The Corinthian Volume 6 Article 4 2004 Comparing Models for Measuring Ring Strain of Common Cycloalkanes Brad A. Hobbs Georgia College Follow this and additional works at: https://kb.gcsu.edu/thecorinthian Part of the Chemistry Commons Recommended Citation Hobbs, Brad A. (2004) "Comparing Models for Measuring Ring Strain of Common Cycloalkanes," The Corinthian: Vol. 6 , Article 4. Available at: https://kb.gcsu.edu/thecorinthian/vol6/iss1/4 This Article is brought to you for free and open access by the Undergraduate Research at Knowledge Box. It has been accepted for inclusion in The Corinthian by an authorized editor of Knowledge Box. Campring Models for Measuring Ring Strain of Common Cycloalkanes Comparing Models for Measuring R..ing Strain of Common Cycloalkanes Brad A. Hobbs Dr. Kenneth C. McGill Chemistry Major Faculty Sponsor Introduction The number of carbon atoms bonded in the ring of a cycloalkane has a large effect on its energy. A molecule's energy has a vast impact on its stability. Determining the most stable form of a molecule is a usefol technique in the world of chemistry. One of the major factors that influ­ ence the energy (stability) of cycloalkanes is the molecule's ring strain. Ring strain is normally viewed as being directly proportional to the insta­ bility of a molecule. It is defined as a type of potential energy within the cyclic molecule, and is determined by the level of "strain" between the bonds of cycloalkanes. For example, propane has tl1e highest ring strain of all cycloalkanes. Each of propane's carbon atoms is sp3-hybridized.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • Today's Class Will Focus on the Conformations and Energies of Cycloalkanes
    Name ______________________________________ Today's class will focus on the conformations and energies of cycloalkanes. Section 6.4 of the text provides an introduction. 1 Make a model of cyclopentane. Use the 2-piece "lockable" bond connectors — these rotate more easily than the smaller ones. You may need to twist them to "lock" so that they don't pop apart. The text shows two conformations of this ring — the envelope and the half-chair. Why is cyclopentane non-planar? The two conformations are below. In the envelope, 4 Cs are in a plane; in the half-chair 3 Cs are in a plane. Th first conformer is easy. To get your model to look like the second one, start with a planar ring, keep the "front" 3 Cs in the plane, and twist the "back" C–C bond so that one C goes above that plane and the other goes below. Add Hs to each of these structures — no wedges and dashes here — these are "perspective" drawings (like the drawings of chair cyclohexane rings on p 197). Just use your model and sketch the Hs where they appear to be. fast If we were to replace one H in each of these conformers with a methyl group, what do you think would be the most favorable position for it? Circle the one H on each structure above that you would replace with a CH3. In general, what happens to the ring C–C–C angles when a ring goes from planar to non-planar? Lecture outline Structures of cycloalkanes — C–C–C angles if planar: 60° 90° 108° 120° actual struct: planar |— slightly |— substantially non-planar —| non-planar —> A compound is strained if it is destabilized by: abnormal bond angles — van der Waals repulsions — eclipsing along σ-bonds — A molecule's strain energy (SE) is the difference between the enthalpy of formation of the compound of interest and that of a hypothetical strain-free compound that has the same atoms connected in exactly the same way.
    [Show full text]
  • Cycloalkanes, Cycloalkenes, and Cycloalkynes
    CYCLOALKANES, CYCLOALKENES, AND CYCLOALKYNES any important hydrocarbons, known as cycloalkanes, contain rings of carbon atoms linked together by single bonds. The simple cycloalkanes of formula (CH,), make up a particularly important homologous series in which the chemical properties change in a much more dramatic way with increasing n than do those of the acyclic hydrocarbons CH,(CH,),,-,H. The cyclo- alkanes with small rings (n = 3-6) are of special interest in exhibiting chemical properties intermediate between those of alkanes and alkenes. In this chapter we will show how this behavior can be explained in terms of angle strain and steric hindrance, concepts that have been introduced previously and will be used with increasing frequency as we proceed further. We also discuss the conformations of cycloalkanes, especially cyclo- hexane, in detail because of their importance to the chemistry of many kinds of naturally occurring organic compounds. Some attention also will be paid to polycyclic compounds, substances with more than one ring, and to cyclo- alkenes and cycloalkynes. 12-1 NOMENCLATURE AND PHYSICAL PROPERTIES OF CYCLOALKANES The IUPAC system for naming cycloalkanes and cycloalkenes was presented in some detail in Sections 3-2 and 3-3, and you may wish to review that ma- terial before proceeding further. Additional procedures are required for naming 446 12 Cycloalkanes, Cycloalkenes, and Cycloalkynes Table 12-1 Physical Properties of Alkanes and Cycloalkanes Density, Compounds Bp, "C Mp, "C diO,g ml-' propane cyclopropane butane cyclobutane pentane cyclopentane hexane cyclohexane heptane cycloheptane octane cyclooctane nonane cyclononane "At -40". bUnder pressure. polycyclic compounds, which have rings with common carbons, and these will be discussed later in this chapter.
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
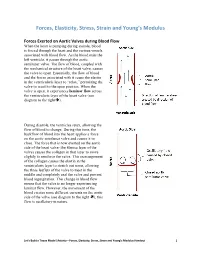
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]
  • Are the Most Well Studied of All Ring Systems. They Have a Limited Number Of, Almost Strain Free, Conformations
    Chem 201/Beauchamp Topic 6, Conformations (cyclohexanes) 1 Cyclohexanes Cyclohexane rings (six atom rings in general) are the most well studied of all ring systems. They have a limited number of, almost strain free, conformations. Because of their well defined conformational shapes, they are frequently used to study effects of orientation or steric effects when studying chemical reactions. Additionally, six atom rings are the most commonly encountered rings in nature. Cyclohexane structures do not choose to be flat. Slight twists at each carbon atom allow cyclohexane rings to assume much more comfortable conformations, which we call chair conformations. (Chairs even sound comfortable.) The chair has an up and down shape all around the ring, sort of like the zig-zag shape seen in straight chains (...time for models!). C C C C C C lounge chair - used to kick back and relax while you study your organic chemistry chair conformation Cyclohexane rings are flexible and easily allow partial rotations (twists) about the C-C single bonds. There is minimal angle strain since each carbon can approximately accommodate the 109o of the tetrahedral shape. Torsional strain energy is minimized in chair conformations since all groups are staggered relative to one another. This is easily seen in a Newman projection perspective. An added new twist to our Newman projections is a side-by-side view of parallel single bonds. If you look carefully at the structure above or use your model, you should be able to see that a parallel relationship exists for all C-C bonds across the ring from one another.
    [Show full text]
  • Thermodynamic Potential of Free Energy for Thermo-Elastic-Plastic Body
    Continuum Mech. Thermodyn. (2018) 30:221–232 https://doi.org/10.1007/s00161-017-0597-3 ORIGINAL ARTICLE Z. Sloderbach´ · J. Paja˛k Thermodynamic potential of free energy for thermo-elastic-plastic body Received: 22 January 2017 / Accepted: 11 September 2017 / Published online: 22 September 2017 © The Author(s) 2017. This article is an open access publication Abstract The procedure of derivation of thermodynamic potential of free energy (Helmholtz free energy) for a thermo-elastic-plastic body is presented. This procedure concerns a special thermodynamic model of a thermo-elastic-plastic body with isotropic hardening characteristics. The classical thermodynamics of irre- versible processes for material characterized by macroscopic internal parameters is used in the derivation. Thermodynamic potential of free energy may be used for practical determination of the level of stored energy accumulated in material during plastic processing applied, e.g., for industry components and other machinery parts received by plastic deformation processing. In this paper the stored energy for the simple stretching of austenitic steel will be presented. Keywords Free energy · Thermo-elastic-plastic body · Enthalpy · Exergy · Stored energy of plastic deformations · Mechanical energy dissipation · Thermodynamic reference state 1 Introduction The derivation of thermodynamic potential of free energy for a model of the thermo-elastic-plastic body with the isotropic hardening is presented. The additive form of the thermodynamic potential is assumed, see, e.g., [1–4]. Such assumption causes that the influence of plastic strains on thermo-elastic properties of the bodies is not taken into account, meaning the lack of “elastic–plastic” coupling effects, see Sloderbach´ [4–10].
    [Show full text]
  • Physical Organic Chemistry
    PHYSICAL ORGANIC CHEMISTRY Yu-Tai Tao (陶雨台） Tel: (02)27898580 E-mail: [email protected] Website:http://www.sinica.edu.tw/~ytt Textbook: “Perspective on Structure and Mechanism in Organic Chemistry” by F. A. Corroll, 1998, Brooks/Cole Publishing Company References: 1. “Modern Physical Organic Chemistry” by E. V. Anslyn and D. A. Dougherty, 2005, University Science Books. Grading: One midterm (45%) one final exam (45%) and 4 quizzes (10%) homeworks Chap.1 Review of Concepts in Organic Chemistry § Quantum number and atomic orbitals Atomic orbital wavefunctions are associated with four quantum numbers: principle q. n. (n=1,2,3), azimuthal q.n. (m= 0,1,2,3 or s,p,d,f,..magnetic q. n. (for p, -1, 0, 1; for d, -2, -1, 0, 1, 2. electron spin q. n. =1/2, -1/2. § Molecular dimensions Atomic radius ionic radius, ri：size of electron cloud around an ion. covalent radius, rc：half of the distance between two atoms of same element bond to each other. van der Waal radius, rvdw：the effective size of atomic cloud around a covalently bonded atoms. - Cl Cl2 CH3Cl Bond length measures the distance between nucleus (or the local centers of electron density). Bond angle measures the angle between lines connecting different nucleus. Molecular volume and surface area can be the sum of atomic volume (or group volume) and surface area. Principle of additivity (group increment) Physical basis of additivity law: the forces between atoms in the same molecule or different molecules are very “short range”. Theoretical determination of molecular size：depending on the boundary condition.
    [Show full text]