DOCSLIB.ORG

PLS Path Modeling with R

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PLS Path Modeling with R PLS Path Modeling with R Gaston Sanchez www.gastonsanchez.com This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License (CC BY-NC-SA 3.0) http://creativecommons.org/licenses/by-nc-sa/3.0/ In short: Gaston Sanchez retains the Copyright but you are free to reproduce, reblog, remix and modify the content only under the same license to this one. You may not use this work for commercial purposes but permission to use this material in nonprofit teaching is still granted, provided the authorship and licensing information here is displayed. Citation Sanchez, G. (2013) PLS Path Modeling with R Trowchez Editions. Berkeley, 2013. http://www.gastonsanchez.com/PLS Path Modeling with R.pdf i To Jessica for her manifest love, her latent support, her outer energy, and her inner strength. I wish my college teachers would have taught many more things than the ones they did. Preferably, I would have liked to be taught more computational courses and programming classes. They taught me the basics but they missed one key lesson that I learned years later with a blend of great disillusionment and enriching experience: the important modeling should take place in the mind of the analyst, not in the computer. Computers and software are indispensable but they can't make sense of data; only people who have developed the necessary data analysis skills can. Whether it is PLS Path Modeling or any other type of modeling, always remember this little-big advice. Optimism Luck Dedication Work Achievement Patience Sacrifice My Model Contents Preface......................................... vii 1 Introduction.................................... 3 1.1 PLS Path Modeling................................ 3 1.2 R package plspm ................................. 5 1.2.1 Why R?.................................. 5 1.3 About Partial Least Squares........................... 6 1.3.1 Short tale of PLS............................. 7 1.3.2 Regressionists and Path-modelists.................... 7 1.4 Structure of the book............................... 8 1.5 R and plspm .................................... 9 1.5.1 Installing plspm .............................. 11 1.5.2 Some Extra Details............................ 12 1.6 Reading List.................................... 13 2 Getting Started with PLS-PM ......................... 15 2.1 Case Study: Index of Success .......................... 15 2.1.1 Of latent and manifest variables..................... 16 2.1.2 Measuring Success, Attack and Defense................. 20 2.1.3 Path Model................................ 21 2.1.4 Inner and Outer models ......................... 22 2.2 Applying PLS-PM with the R package plspm . 23 2.2.1 Preparing the ingredients for plspm() . 24 2.2.2 Running plspm() ............................. 26 2.2.3 Plotting results.............................. 29 2.3 Reading List.................................... 31 3 Setting the PLS-PM Framework........................ 33 3.1 PLS-PM Frame of Mind ............................. 33 3.2 PLS Path Modeling Specs ............................ 35 3.3 Formal Model: What we want .......................... 35 3.3.1 The Structural Model........................... 36 3.3.2 The Measurement Model......................... 37 v 3.3.3 The Weight Relations........................... 38 3.4 Operative Model: How to get what we want . 39 3.4.1 Stage 1: Iterative Process ........................ 41 3.4.2 Stage 2: Path Coefficients ........................ 46 3.4.3 Stage 3: Loadings............................. 46 3.4.4 Wrapping up ............................... 46 3.5 Reading List.................................... 47 4 Interpreting PLS-PM Results.......................... 49 4.1 Reminder of Our Success Index Model ..................... 50 4.1.1 PLS-PM with plspm ........................... 50 4.1.2 The function plspm() .......................... 51 4.2 Handling PLS-PM results ............................ 54 4.3 Measurement Model Assessment: Reflective Indicators ............................... 55 4.3.1 All for one and one for all ........................ 55 4.3.2 Unidimensionality of indicators ..................... 56 4.3.3 Loadings and Communalities ...................... 62 4.3.4 Cross-loadings............................... 64 4.4 Measurement Model Assessment: Formative Indicators............................... 67 4.5 Structural Model Assessment .......................... 67 4.5.1 Coefficients of determination R2 ..................... 68 4.5.2 Redundancy................................ 68 4.5.3 GoF .................................... 69 4.6 Validation..................................... 70 4.6.1 Bootstrapping............................... 70 4.7 Reading List.................................... 72 5 Running a PLS-PM Analysis.......................... 75 5.1 Modeling Customer Satisfaction......................... 75 5.1.1 ECSI Model................................ 76 5.1.2 Case Study: Satisfaction in Education ................. 77 5.2 Preliminary Exploration ............................. 81 5.2.1 Looking at the data............................ 82 5.2.2 Seeing the forest, not just the trees................... 84 5.3 PLS-PM Round 1................................. 86 5.4 PLS-PM Round 2................................. 90 5.5 PLS-PM Round 3................................. 94 5.5.1 Checking unidimensionality ....................... 94 5.5.2 Loadings and Communalities ...................... 95 5.5.3 Path Coefficients ............................. 97 5.5.4 Structural Regressions .......................... 99 5.5.5 Effects................................... 100 5.5.6 Inner Model Summary.......................... 103 5.5.7 GoF .................................... 104 5.5.8 Bootstrap Validation........................... 105 5.5.9 Inspecting scores of latent variables................... 108 5.6 Guidelines for a PLS-PM analysis........................ 111 5.7 Reading List.................................... 113 6 Comparing Groups ................................117 6.1 The million dollar question............................ 117 6.2 Group Comparison Approaches ......................... 119 6.2.1 Bootstrap t-test.............................. 120 6.2.2 Permutation Procedure.......................... 121 6.2.3 Case Study: College GPA ........................ 122 6.2.4 PLS-PM Analysis: GPA Model ..................... 125 6.2.5 Female and Male Student Models.................... 128 6.3 Comparing Groups: Bootstrap t-test ...................... 129 6.4 Comparing Groups: Permutation test...................... 131 6.5 Reading List.................................... 133 7 Moderating Effects ................................135 7.1 Moderator Variables ............................... 135 7.2 Moderating effects in PLS-PM.......................... 136 7.2.1 Moderator variables as constructs.................... 137 7.2.2 Case Study: Simplified Customer Satisfaction . 137 7.3 Product Indicator Approach........................... 138 7.3.1 Example.................................. 139 7.4 Two-Stage Path Modeling Approach ...................... 143 7.4.1 Example.................................. 144 7.5 Two-Stage Regression Approach......................... 147 7.5.1 Example.................................. 148 7.6 Categorical Variable Approach.......................... 151 7.6.1 Example.................................. 152 7.7 Reading List.................................... 155 8 PLS Path Models with Higher-Order Constructs . 157 8.1 Constructify-it: How to model higher-order constructs? .................................... 158 8.1.1 Two types of higher-order constructs .................. 159 8.1.2 Modeling higher-order constructs in PLS-PM . 160 8.1.3 Case Study: NFL data.......................... 161 viii 8.2 Repeated Indicators: The Poor Man's Approach . 164 8.2.1 Repeated Indicators example ...................... 165 8.3 Two-Step Option: The Patch Approach . 167 8.3.1 Two-Step example ............................ 167 8.4 Hybrid Option: The Give Away Approach . 172 8.4.1 Hybrid Approach example........................ 172 8.5 Wrapping Up ................................... 173 8.6 Reading List.................................... 175 9 Detecting Classes with REBUS-PLS......................177 9.1 Diversity in Data................................. 177 9.1.1 Unobserved Classes............................ 178 9.2 What is REBUS?................................. 179 9.2.1 The REBUS Approach.......................... 179 9.2.2 Case Study: Success Index Model.................... 181 9.2.3 Global PLS Path Model ......................... 182 9.3 Applying REBUS................................. 188 9.3.1 Local Models ............................... 193 9.3.2 Quality of REBUS models........................ 198 9.3.3 Final Comments ............................. 201 9.4 Reading List.................................... 201 A Historical Overview of PLS-PM ........................205 1 Preliminaries ................................... 205 2 Herman Wold................................... 208 2.1 The Econometrician ........................... 209 2.2 The Least Squares Affair......................... 210 2.3 The Philosopher of Science........................ 213 3 Pre-PLS Era.................................... 214 4 Soft Modeling................................... 217 5 PLS-PM Related Timeline............................ 218 6 Reading List.................................... 221 CC BY-NC-SA 3.0 Gaston Sanchez PLS Path Modeling with R Preface On a sunny September morning
Load more

Recommended publications
  • University of Pardubice
    UNIVERSITY OF PARDUBICE FACULTY OF ECONOMICS AND ADMINISTRATION Institute of Economic Sciences EVALUATION OF THE ROLE OF CRUCIAL IMPACTS ON NETWORKS FOR TECHNOLOGICAL INNOVATION Ing. Anderson, Henry Junior SUPERVISOR: Assoc. Prof. Ing. Jan Stejskal, Ph.D. Dissertation thesis 2020 TABLE OF CONTENTS INTRODUCTION ..................................................................................................................... 1 1. CONCEPTUAL FRAMEWORK ................................................................................... 3 1.1. Innovation Systems: Technological Innovation Systems............................................ 3 1.1.1. Functional Processes of Technological Innovation System................................. 4 1.1.2. Emergence and Renewed Direction of Technological Innovation System ......... 7 1.2. Contemporary Indicators of Modern Technological Innovation................................. 9 1.2.1. Research Systems................................................................................................. 9 1.2.2. Financial Cradles ............................................................................................... 10 1.2.3. Human Capital ................................................................................................... 12 1.2.4. Cooperation ........................................................................................................ 13 1.3. Regional Attractiveness for Innovation and Foreign Direct Investments ................. 14 1.4. Innovation Indicators’ Contribution
    [Show full text]
  • Econometrics
    BIBLIOGRAPHY ISSUE 28, OCTOBER-NOVEMBER 2013 Econometrics http://library.bankofgreece.gr http://library.bankofgreece.gr Tables of contents Introduction...................................................................................................................2 I. Print collection of the Library...........................................................................................3 I.1 Monographs .................................................................................................................3 I.2 Periodicals.................................................................................................................. 33 II. Electronic collection of the Library ................................................................................ 35 II.1 Full text articles ..................................................................................................... 35 IΙI. Resources from the World Wide Web ......................................................................... 59 IV. List of topics published in previous issues of the Bibliography........................................ 61 Image cover: It has created through the website http://www.wordle.net All the issues are available at the internet: http://www.bankofgreece.gr/Pages/el/Bank/Library/news.aspx Bank of Greece / Centre for Culture, Research and Documentation / Library Unit / 21 El. Venizelos, 102 50 Athens / [email protected]/ Tel. 210 320 2446, 2522 / Bibliography: bimonthly electronic edition, Issue 28, September- October 2013 Contributors:
    [Show full text]
  • Organizational Capabilities for Family Firm Sustainability: the Role of Knowledge Accumulation and Family Essence
    sustainability Article Organizational Capabilities for Family Firm Sustainability: The Role of Knowledge Accumulation and Family Essence Ismael Barros-Contreras 1, Jesús Manuel Palma-Ruiz 2,* and Angel Torres-Toukoumidis 3 1 Instituto de Gestión e Industria, Universidad Austral de Chile, Valdivia 5480000, Chile; [email protected] 2 Facultad de Contaduría y Administración, Universidad Autónoma de Chihuahua, Chihuahua 31000, Mexico 3 Social Science Knowledge and Human Behavior, Universidad Politécnica Salesiana, Cuenca 010105, Ecuador; [email protected] * Correspondence: [email protected] Abstract: While prior studies recognize the importance of organizational capabilities for family firm sustainability, current research has still failed to empirically identify the role of different types of knowledge accumulation with regard to these organizational capabilities. Based on the dynamic capabilities theory, the main goal of this paper is to address this research gap and to explore the rela- tionships between both internal and external knowledge accumulation, and ordinary organizational capabilities. This research also contributes to analyzing the complex effect of the family firm essence, influenced by both family involvement and generational involvement levels, as an antecedent of internal and external knowledge accumulation. Our analysis of 102 non-listed Spanish family firms shows that the family firm essence, which is influenced by the family involvement, strengthens only the internal knowledge accumulation but not the external one. Furthermore, our study also reveals Citation: Barros-Contreras, I.; that both internal and knowledge accumulation are positively related to ordinary capabilities. Palma-Ruiz, J.M.; Torres-Toukoumidis, A. Keywords: dynamic capabilities; internal knowledge accumulation; external knowledge accumu- Organizational Capabilities for lation; family essence; family firms; ordinary capabilities; structural equation modeling; partial Family Firm Sustainability: The Role least squares of Knowledge Accumulation and Family Essence.
    [Show full text]
  • Overview-Of-Statistical-Analytics-And
    Brief Overview of Statistical Analytics and Machine Learning tools for Data Scientists Tom Breur 17 January 2017 It is often said that Excel is the most commonly used analytics tool, and that is hard to argue with: it has a Billion users worldwide. Although not everybody thinks of Excel as a Data Science tool, it certainly is often used for “data discovery”, and can be used for many other tasks, too. There are two “old school” tools, SPSS and SAS, that were founded in 1968 and 1976 respectively. These products have been the hallmark of statistics. Both had early offerings of data mining suites (Clementine, now called IBM SPSS Modeler, and SAS Enterprise Miner) and both are still used widely in Data Science, today. They have evolved from a command line only interface, to more user-friendly graphic user interfaces. What they also share in common is that in the core SPSS and SAS are really COBOL dialects and are therefore characterized by row- based processing. That doesn’t make them inherently good or bad, but it is principally different from set-based operations that many other tools offer nowadays. Similar in functionality to the traditional leaders SAS and SPSS have been JMP and Statistica. Both remarkably user-friendly tools with broad data mining and machine learning capabilities. JMP is, and always has been, a fully owned daughter company of SAS, and only came to the fore when hardware became more powerful. Its initial “handicap” of storing all data in RAM was once a severe limitation, but since computers now have large enough internal memory for most data sets, its computational power and intuitive GUI hold their own.
    [Show full text]
  • Statistics and GIS Assistance Help with Statistics
    Statistics and GIS assistance An arrangement for help and advice with regard to statistics and GIS is now in operation, principally for Master’s students. How do you seek advice? 1. The users, i.e. students at INA, make direct contact with the person whom they think can help and arrange a time for consultation. Remember to be well prepared! 2. Doctoral students and postdocs register the time used in Agresso (if you have questions about this contact Gunnar Jensen). Help with statistics Research scientist Even Bergseng Discipline: Forest economy, forest policies, forest models Statistical expertise: Regression analysis, models with random and fixed effects, controlled/truncated data, some time series modelling, parametric and non-parametric effectiveness analyses Software: Stata, Excel Postdoc. Ole Martin Bollandsås Discipline: Forest production, forest inventory Statistics expertise: Regression analysis, sampling Software: SAS, R Associate Professor Sjur Baardsen Discipline: Econometric analysis of markets in the forest sector Statistical expertise: General, although somewhat “rusty”, expertise in many econometric topics (all-rounder) Software: Shazam, Frontier Associate Professor Terje Gobakken Discipline: GIS og long-term predictions Statistical expertise: Regression analysis, ANOVA and PLS regression Software: SAS, R Ph.D. Student Espen Halvorsen Discipline: Forest economy, forest management planning Statistical expertise: OLS, GLS, hypothesis testing, autocorrelation, ANOVA, categorical data, GLM, ANOVA Software: (partly) Shazam, Minitab og JMP Ph.D. Student Jan Vidar Haukeland Discipline: Nature based tourism Statistical expertise: Regression and factor analysis Software: SPSS Associate Professor Olav Høibø Discipline: Wood technology Statistical expertise: Planning of experiments, regression analysis (linear and non-linear), ANOVA, random and non-random effects, categorical data, multivariate analysis Software: R, JMP, Unscrambler, some SAS Ph.D.
    [Show full text]
  • Indian Statistical Institute
    CHAPTER VII INDIAN STATISTICAL INSTITUTE 7.1 The Indian Statistical Institute (ISI) came into being with the pioneering initiative and efforts of Professor P.C. Mahalanobis in early thirties (registered on 28 April, 1932). The Institute expanded its research, teaching, training and project activities and got national/international recognitions. The Institute was recognized as an “Institute of National Importance” by an Act of Parliament, known as “Indian Statistical Institute Act No.57 of 1959”. Significantly, Pandit Jawaharlal Nehru, the then Prime Minister piloted the bill in the Parliament in 1959. This Act conferred the right to hold examinations and award degrees/diplomas in Statistics. Degree courses viz. Bachelor of Statistics (B.Stat.), Master of Statistics (M.Stat.) and post graduate diplomas in SQC & OR and Computer Science were started from June 1960. The Institute was also empowered to award Ph.D./D.Sc. degree from the same year. Subsequently, Master of Technology courses in Computer Science and in Quality, Reliability & Operations Research were also started. The Institute’s scope was further enlarged to award degrees/diplomas in Statistics, Mathematics, Quantitative Economics, Computer Science and such other subjects related to Statistics by virtue of “Indian Statistical Institute (Amendment) Act, 1995. The Institute took up research activities not only in Statistics/Mathematics but also in Natural and Social Sciences, Physics and Earth Sciences, Biological Sciences, Statistical Quality Control & Operations Research and Library and Information Sciences. 7.2 Sankhya – The Indian Journal of Statistics, being published by the Institute since 1933, is considered as one of the leading Statistical Journals of the world.
    [Show full text]
  • Construction of a Neuro-Immune-Cognitive Pathway-Phenotype Underpinning the Phenome Of
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 20 October 2019 doi:10.20944/preprints201910.0239.v1 Construction of a neuro-immune-cognitive pathway-phenotype underpinning the phenome of deficit schizophrenia. Hussein Kadhem Al-Hakeima, Abbas F. Almullab, Arafat Hussein Al-Dujailic, Michael Maes d,e,f. a Department of Chemistry, College of Science, University of Kufa, Iraq. E-mail: [email protected]. b Medical Laboratory Technology Department, College of Medical Technology, The Islamic University, Najaf, Iraq. E-mail: [email protected]. c Senior Clinical Psychiatrist, Faculty of Medicine, Kufa University. E-mail: [email protected]. d* Department of Psychiatry, Faculty of Medicine, Chulalongkorn University, Bangkok, Thailand; e Department of Psychiatry, Medical University of Plovdiv, Plovdiv, Bulgaria; f IMPACT Strategic Research Centre, Deakin University, PO Box 281, Geelong, VIC, 3220, Australia. Corresponding author Prof. Dr. Michael Maes, M.D., Ph.D. Department of Psychiatry Faculty of Medicine Chulalongkorn University Bangkok Thailand 1 © 2019 by the author(s). Distributed under a Creative Commons CC BY license. Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 20 October 2019 doi:10.20944/preprints201910.0239.v1 https://scholar.google.co.th/citations?user=1wzMZ7UAAAAJ&hl=th&oi=ao [email protected]. 2 Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 20 October 2019 doi:10.20944/preprints201910.0239.v1 Abstract In schizophrenia, pathway-genotypes may be constructed by combining interrelated immune biomarkers with changes in specific neurocognitive functions that represent aberrations in brain neuronal circuits. These constructs provide insight on the phenome of schizophrenia and show how pathway-phenotypes mediate the effects of genome X environmentome interactions on the symptomatology/phenomenology of schizophrenia.
    [Show full text]
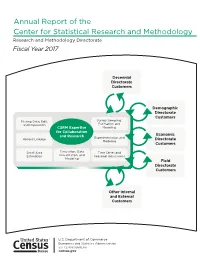
  • Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
    Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S.
    [Show full text]
  • Gröbner Basis and Structural Equation Modeling by Min Lim a Thesis
    Grobner¨ Basis and Structural Equation Modeling by Min Lim A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Statistics University of Toronto Copyright c 2010 by Min Lim Abstract Gr¨obnerBasis and Structural Equation Modeling Min Lim Doctor of Philosophy Graduate Department of Statistics University of Toronto 2010 Structural equation models are systems of simultaneous linear equations that are gener- alizations of linear regression, and have many applications in the social, behavioural and biological sciences. A serious barrier to applications is that it is easy to specify models for which the parameter vector is not identifiable from the distribution of the observable data, and it is often difficult to tell whether a model is identified or not. In this thesis, we study the most straightforward method to check for identification – solving a system of simultaneous equations. However, the calculations can easily get very complex. Gr¨obner basis is introduced to simplify the process. The main idea of checking identification is to solve a set of finitely many simultaneous equations, called identifying equations, which can be transformed into polynomials. If a unique solution is found, the model is identified. Gr¨obner basis reduces the polynomials into simpler forms making them easier to solve. Also, it allows us to investigate the model-induced constraints on the covariances, even when the model is not identified. With the explicit solution to the identifying equations, including the constraints on the covariances, we can (1) locate points in the parameter space where the model is not iden- tified, (2) find the maximum likelihood estimators, (3) study the effects of mis-specified models, (4) obtain a set of method of moments estimators, and (5) build customized parametric and distribution free tests, including inference for non-identified models.
    [Show full text]
  • Partial Least Squares Path Modeling Hengky Latan • Richard Noonan Editors
    Partial Least Squares Path Modeling Hengky Latan • Richard Noonan Editors Partial Least Squares Path Modeling Basic Concepts, Methodological Issues and Applications 123 Editors Hengky Latan Richard Noonan Department of Accounting Institute of International Education STIE Bank BPD Jateng and Petra Stockholm University Christian University Stockholm, Sweden Semarang-Surabaya, Indonesia ISBN 978-3-319-64068-6 ISBN 978-3-319-64069-3 (eBook) DOI 10.1007/978-3-319-64069-3 Library of Congress Control Number: 2017955377 Mathematics Subject Classification (2010): 62H20, 62H25, 62H12, 62F12, 62F03, 62F40, 65C05, 62H30 © Springer International Publishing AG 2017 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made.
    [Show full text]
  • Fibrinogen Levels Are Associated with Lymph Node Involvement And
    ANTICANCER RESEARCH 38 : 1097-1104 (2018) doi:10.21873/anticanres.12328 Fibrinogen Levels Are Associated with Lymph Node Involvement and Overall Survival in Gastric Cancer Patients JÚLIUS PALAJ 1, ŠTEFAN KEČKÉŠ 2, VÍTĚZSLAV MAREK 1, DANIEL DYTTERT 1, IVETA WACZULÍKOVÁ 3 and ŠTEFAN DURDÍK 1 1Department of Oncological Surgery, St. Elizabeth Cancer Institute, Slovak Republic and Faculty of Medicine in Bratislava of the Comenius University, Bratislava, Slovak Republic; 2Department of Immunodiagnostics, St. Elizabeth Cancer Institute, Bratislava, Slovak Republic; 3Department of Nuclear Physics and Biophysics, Comenius University, Faculty of Mathematics, Physics and Informatics, Bratislava, Slovak Republic Abstract. Background/Aim: Combination of perioperative accounting for 6.8% of all diagnosed cancers and making this chemotherapy with gastrectomy with D2 lymphadenectomy cancer the 5th most common malignancy globally (2). improves long-term survival in patients with gastric cancer. Moreover, it is the third leading cause of death in both sexes The aim of this study was to investigate the predictive value accounting for 8.8% of the total deaths from cancer (3). of preoperative levels of CRP, albumin, fibrinogen, In spite of advancements in chemotherapy and local neutrophil-to-lymphocyte ratio and routinely used tumor control of GC, prognosis remains poor, mainly because of markers (CEA, CA 19-9, CA 72-4) for lymph node the advancement of the disease at the time of diagnosis. involvement. Materials and Methods: This retrospective Approximately 50% patients in western countries have study was conducted in 136 patients who underwent surgery metastases at the time of diagnosis, and from those without between 2007 and 2015. Bivariable and multivariable metastatic disease only 50% are eligible for gastric resection analyses were performed in order to identify important (4).
    [Show full text]
  • Towards a Fully Automated Extraction and Interpretation of Tabular Data Using Machine Learning
    UPTEC F 19050 Examensarbete 30 hp August 2019 Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Per Hedbrant Master Thesis in Engineering Physics Department of Engineering Sciences Uppsala University Sweden Abstract Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Teknisk- naturvetenskaplig fakultet UTH-enheten Motivation A challenge for researchers at CBCS is the ability to efficiently manage the Besöksadress: different data formats that frequently are changed. Significant amount of time is Ångströmlaboratoriet Lägerhyddsvägen 1 spent on manual pre-processing, converting from one format to another. There are Hus 4, Plan 0 currently no solutions that uses pattern recognition to locate and automatically recognise data structures in a spreadsheet. Postadress: Box 536 751 21 Uppsala Problem Definition The desired solution is to build a self-learning Software as-a-Service (SaaS) for Telefon: automated recognition and loading of data stored in arbitrary formats. The aim of 018 – 471 30 03 this study is three-folded: A) Investigate if unsupervised machine learning Telefax: methods can be used to label different types of cells in spreadsheets. B) 018 – 471 30 00 Investigate if a hypothesis-generating algorithm can be used to label different types of cells in spreadsheets. C) Advise on choices of architecture and Hemsida: technologies for the SaaS solution. http://www.teknat.uu.se/student Method A pre-processing framework is built that can read and pre-process any type of spreadsheet into a feature matrix. Different datasets are read and clustered. An investigation on the usefulness of reducing the dimensionality is also done.
    [Show full text]