Valuing Individual Player Involvements in Norwegian Association Football
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

European Qualifiers
EUROPEAN QUALIFIERS - 2014/16 SEASON MATCH PRESS KITS Helsinki Olympic Stadium - Helsinki Saturday 11 October 2014 20.45CET (21.45 local time) Finland Group F - Matchday -11 Greece Last updated 12/07/2021 16:57CET Official Partners of UEFA EURO 2020 Previous meetings 2 Match background 4 Squad list 5 Head coach 7 Match officials 8 Competition facts 9 Match-by-match lineups 10 Team facts 12 Legend 14 1 Finland - Greece Saturday 11 October 2014 - 20.45CET (21.45 local time) Match press kit Helsinki Olympic Stadium, Helsinki Previous meetings Head to Head FIFA World Cup Stage Date Match Result Venue Goalscorers reached Forssell 14, 45, Riihilahti 21, Kolkka 05/09/2001 QR (GS) Finland - Greece 5-1 Helsinki 38, Litmanen 53; Karagounis 30 07/10/2000 QR (GS) Greece - Finland 1-0 Athens Liberopoulos 59 EURO '96 Stage Date Match Result Venue Goalscorers reached Litmanen 44, Hjelm 11/06/1995 PR (GS) Finland - Greece 2-1 Helsinki 54; Nikolaidis 6 Markos 22, Batista 69, 12/10/1994 PR (GS) Greece - Finland 4-0 Salonika Machlas 76, 89 EURO '92 Stage Date Match Result Venue Goalscorers reached Saravakos 49, 30/10/1991 PR (GS) Greece - Finland 2-0 Athens Borbokis 51 Ukkonen 50; 09/10/1991 PR (GS) Finland - Greece 1-1 Helsinki Tsalouchidis 74 1980 UEFA European Championship Stage Date Match Result Venue Goalscorers reached Nikoloudis 15, 25, Delikaris 23, 47, 11/10/1978 PR (GS) Greece - Finland 8-1 Athens Mavros 38, 44, 75 (P), Galakos 81; Heiskanen 61 Ismail 35, 82, 24/05/1978 PR (GS) Finland - Greece 3-0 Helsinki Nieminen 80 1968 UEFA European Championship -

European Qualifiers
EUROPEAN QUALIFIERS - 2016/18 SEASON MATCH PRESS KITS Tampere Stadium - Tampere Sunday 9 October 2016 18.00CET (19.00 local time) Finland Group I - Matchday 3 Croatia Last updated 09/10/2016 16:29CET EUROPEAN QUALIFIERS OFFICIAL SPONSORS Squad list 2 Legend 4 1 Finland - Croatia Sunday 9 October 2016 - 18.00CET (19.00 local time) Match press kit Tampere Stadium, Tampere Squad list Finland Current season Qual. FT No. Player DoB Age Club D Pld Gls Pld Gls Goalkeepers - Niki Mäenpää 23/01/1985 31 Brighton - 0 0 0 0 - Lukas Hradecky 24/11/1989 26 Frankfurt * 2 0 0 0 - Jesse Joronen 21/03/1993 23 Fulham - 0 0 0 0 Defenders - Niklas Moisander 29/09/1985 31 Bremen * 2 0 0 0 - Markus Halsti 19/03/1984 32 Midtjylland * 2 0 0 0 - Kari Arkivuo 23/06/1983 33 Häcken - 1 0 0 0 - Jukka Raitala 15/09/1988 28 Sogndal - 2 0 0 0 - Juhani Ojala 19/06/1989 27 Seinäjoki - 0 0 0 0 - Paulus Arajuuri 15/06/1988 28 Lech * 2 1 0 0 - Thomas Lam 18/12/1993 22 Nottm Forest * 1 0 0 0 - Janne Saksela 14/03/1993 23 RoPS - 0 0 0 0 - Sauli Väisänen 05/06/1994 22 AIK * 1 0 0 0 - Albin Granlund 01/09/1989 27 Mariehamn - 0 0 0 0 Midfielders - Kasper Hämäläinen 08/08/1986 30 Legia - 2 0 0 0 - Perparim Hetemaj 12/12/1986 29 Chievo - 1 0 0 0 - Joni Kauko 12/07/1990 26 Randers - 0 0 0 0 - Sakari Mattila 14/07/1989 27 SønderjyskE - 0 0 0 0 - Rasmus Schüller 18/06/1991 25 Häcken - 2 0 0 0 - Alexander Ring 09/04/1991 25 Kaiserslautern - 2 0 0 0 - Robin Lod 17/04/1993 23 Panathinaikos - 2 1 0 0 Forwards - Teemu Pukki 29/03/1990 26 Brøndby - 2 1 0 0 - Roope Riski 16/08/1991 25 Seinäjoki - 0 0 0 0 - Eero Markkanen 03/07/1990 26 AIK - 1 0 0 0 Coach - Hans Backe 14/02/1952 64 - 2 0 0 0 2 Finland - Croatia Sunday 9 October 2016 - 18.00CET (19.00 local time) Match press kit Tampere Stadium, Tampere Croatia Current season Qual. -

Uefa Champions League
UEFA CHAMPIONS LEAGUE - 2017/18 SEASON MATCH PRESS KITS Estádio do Sport Lisboa e Benfica - Lisbon Tuesday 12 September 2017 SL Benfica 20.45CET (19.45 local time) PFC CSKA Moskva Group A - Matchday 1 Last updated 31/05/2018 02:07CET UEFA CHAMPIONS LEAGUE OFFICIAL SPONSORS Previous meetings 2 Match background 5 Squad list 7 Head coach 9 Match officials 10 Fixtures and results 12 Match-by-match lineups 15 Competition facts 17 Team facts 18 Legend 20 1 SL Benfica - PFC CSKA Moskva Tuesday 12 September 2017 - 20.45CET (19.45 local time) Match press kit Estádio do Sport Lisboa e Benfica, Lisbon Previous meetings Head to Head UEFA Cup Date Stage Match Result Venue Goalscorers 1-1 Karadas 63; 24/02/2005 R3 SL Benfica - PFC CSKA Moskva Lisbon agg: 1-3 Ignashevich 49 V. Berezutski 12, 17/02/2005 R3 PFC CSKA Moskva - SL Benfica 2-0 Krasnodar Vágner Love 60 Home Away Final Total Pld W D L Pld W D L Pld W D L Pld W D L GF GA SL Benfica 1 0 1 0 1 0 0 1 0 0 0 0 2 0 1 1 1 3 PFC CSKA Moskva 1 1 0 0 1 0 1 0 0 0 0 0 2 1 1 0 3 1 SL Benfica - Record versus clubs from opponents' country UEFA Champions League Date Stage Match Result Venue Goalscorers 1-2 Hulk 69; Gaitán 85, 09/03/2016 R16 FC Zenit - SL Benfica St Petersburg agg: 1-3 Talisca 90+6 16/02/2016 R16 SL Benfica - FC Zenit 1-0 Lisbon Jonas 90+1 UEFA Champions League Date Stage Match Result Venue Goalscorers 26/11/2014 GS FC Zenit - SL Benfica 1-0 St Petersburg Danny 79 16/09/2014 GS SL Benfica - FC Zenit 0-2 Lisbon Hulk 5, Witsel 22 UEFA Champions League Date Stage Match Result Venue Goalscorers -
E 1 0 3 0 F 2 1
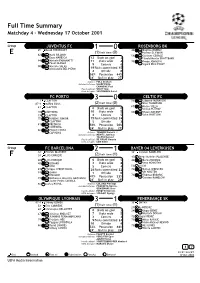
Full Time Summary Matchday 4 - Wednesday 17 October 2001 Group JUVENTUS FC ROSENBORG BK 25' David TREZEGUET 1046' in Dagfinn ENERLY (1)half time (0) out Hassan EL FAKIRI E in 62' Mark IULIANO in out 59' Christer GEORGE Enzo MARESCA 12 Shots on goal 2 out Harald Martin BRATTBAKK in 84' Michele PARAMATTI 11 Shots wide 4 in out 75' Frode JOHNSEN Pavel NEDVED 9 Corners 6 out Sigurd RUSHFELDT 90' in Marcelo SALAS out Alessandro DEL PIERO 19 Fouls committed 15 4 Offside 0 56% Possession 44% 34' Ball in play 27' Referee: POLL Graham Assistant referees: SHARP Philip CANADINE Paul Fourth official: WILEY Alan UEFA delegate: VERTONGEN Karel FC PORTO30 CELTIC FC 1' CLAYTON 56' in Lubomir MORAVCIK 45'+1 MÁRIO SILVA (2)half time (0) out Alan THOMPSON 61' CLAYTON 67' in Momo SYLLA 8 Shots on goal 0 out Stilian PETROV 10' CÔSTINHA 10 Shots wide 5 88' in Shaun MALONEY 19' CLAYTON 4 Corners 5 out John HARTSON 75' in RUBENS JUNIOR 15 Fouls committed 24 out CLAYTON 5 Offside 3 81' in FREDRICK 50% Possession 50% out CÔSTINHA 24' Ball in play 23' 86' in PAULO COSTA out CAPUCHO Referee: TEMMINK René H.J. Assistant referees: MEINTS Jantinus TALENS Berend Fourth official: DE GRAAF Hennie UEFA delegate: COX Eddie Group FC BARCELONA BAYER 04 LEVERKUSEN 12' Patrick KLUIVERT 2132' Carsten RAMELOW 38' LUIS ENRIQUE (2)half time (1) F 45' Diego Rodolfo PLACENTE 20' LUIS ENRIQUE 6 Shots on goal 5 46' in Boris ZIVKOVIC out 48' in GERARD 3 Shots wide 6 Jens NOWOTNY out XAVI 5 Corners 4 53' LUCIO 69' Philippe CHRISTANVAL 28 Fouls committed 22 76' in Zoltan SEBESCEN out -

Rebuilding Efforts to Take Years News Officials Estimate All Schools in Oslo Were Evacu- Ated Oct
(Periodicals postage paid in Seattle, WA) TIME-DATED MATERIAL — DO NOT DELAY News In Your Neighborhood A Midwest Celebrating 25 welcome Se opp for dem som bare vil years of Leif leve sitt liv i fred. to the U.S. De skyr intet middel. Erikson Hall Read more on page 3 – Claes Andersson Read more on page 13 Norwegian American Weekly Vol. 122 No. 38 October 21, 2011 Established May 17, 1889 • Formerly Western Viking and Nordisk Tidende $1.50 per copy Norway.com News Find more at www.norway.com Rebuilding efforts to take years News Officials estimate All schools in Oslo were evacu- ated Oct. 12 closed due to it could take five danger of explosion in school years and NOK 6 fire extinguishers. “There has been a manufacturing defect billion to rebuild discovered in a series of fire extinguishers used in schools government in Oslo. As far as I know there buildings have not been any accidents be- cause of this,” says Ron Skaug at the Fire and Rescue Service KELSEY LARSON in Oslo. Schools in Oslo were Copy Editor either closed or had revised schedules the following day. (blog.norway.com/category/ Government officials estimate news) that it may take five years and cost NOK 6 billion (approximately Culture USD 1 billion) to rebuild the gov- American rapper Snoop Dogg ernment buildings destroyed in the was held at the Norwegian bor- aftermath of the July 22 terrorist der for having “too much cash.” attacks in Oslo. He was headed to an autograph Rigmor Aasrud, a member of signing at an Adidas store on the Labor Party and Minister of Oct. -

Troms Fotballkrets Årbok 2016
TROMS FOTBALLKRETS ÅRBOK 2016 Foto: Thomas Brekke Sæteren, NFF Troms Fotballkrets´42. kretsting 18.-19. februar 2017 Scandic Grand Tromsø tromsprodukt.no #folkijobb Vi samarbeider med idretten SCANDIC GRAND TROMSØ – HOTELLET I HJERTET AV TROMSØ VISSTE DU Restauranten på Scandic Grand tilbyr stor frokostbuffet hver dag. at vi har grafiske designere som kan hjelpe deg Vår Gründer Café & Bar serverer lunsj og middag i en uformell atmosfære. med ditt markedsføringsmateriell? Bestill på tlf: 77 75 37 77 / epost: [email protected] Ta kontakt med Christina Grytå: [email protected] eller tlf 982 49 533 Velkommen! www.scandichotels.no - garantert best pris Troms Fotballkrets – kretstinget 18.-19.02.17 INNHOLDSFORTEGNELSE Program for kretstinget. ……………………………………………… 4 Saksliste for kretstinget. ……………………………………………… 4 Tale-, stemme- og forslagsrett ………………………………………. 5 Representasjonsskala ………………………………………………... 5 Forretningsorden for kretstinget. …………………………………….. 6 Styrets årsberetning. …………………………………………………. 6 Kretsstyret og tingvalgte komiteer. ………………………………….. 8 Administrasjonen. …………………………………………………… 8 Komiteer oppnevnt av styret. ……………………………………..…. 9 Klubbene i Troms Fotballkrets ……………………………………… 10 Antall lag i Troms Fotballkrets ………….……………….……….... 11 Saker fra 2016……………………………………………………….. 13 NFFs Handlingsplan 2016-2019 – lokale tilpassinger ………………. 25 Norgesmesterskapene. ………………………………………………. 29 Kretsmesterskap og avdelingsmesterskap. …………………………. 31 Kretsmestere og avdelingsvinnere. ……………….……………….. 33 Futsal. ………………………………………………………………… -

Rosenborg Ballklub
Årsmelding2019 Rosenborg Ballklub w Foto: Arve Johnsen, Digitalsport Hovedsamarbeidspartner Samarbeidspartnere Årsmelding for Rosenborg Ballklub 2019 Innhold 4. Dagsorden 5. Forslag til forretningsorden 6. Styrets og daglig leders beretning 10. Organisasjon 12. A-laget 15. A-kamper i 2019 17. SalMar Akademiet 20. Samfunnsansvar 22. RBKs Veteranlaug årsberetning 2019 24. Kontrollkomiteens beretning for 2019 25. Forslag til årsmøtet 38. Innstilling av tillitsvalgte 39. Lov for Rosenborg Ballklub 47. Referat fra årsmøtet i Rosenborg Ballklub 2018 51. Adelskalender Rosenborg Ballklub Innhold 3 Årsmelding for Rosenborg Ballklub 2019 Dagsorden 1. Godkjenning av stemmeberettigede. 2. Godkjenning av innkalling, saksliste og forretningsorden. 3. Valg av dirigent og sekretær. 4. Valg av to medlemmer til å undertegne årsmøteprotokollen. 5. Behandle årsmelding fra styret, utvalg og komiteer. 6. Behandle regnskap for klubben og konsernregnskap i revidert stand. 7. Behandle innkomne forslag og saker. Herunder skal årsmøtet kunne behandle enhver sak som er av prinsipiell art eller av stor betydning, og som kan innebære betydelige økonomiske forpliktelser for klubben. 8. Fastsette medlemskontingent. 9. Vedta klubbens budsjett. 10. Behandle klubbens organisasjonsplan. 11. Engasjere statsautorisert revisor til å revidere klubbens regnskap og fastsette dennes honorar. 12. Foreta følgende valg: a. Leder og nestleder. b. 5 styremedlemmer for 2 år og 1 varamedlem for 1 år. Valgt styre i klubben fungerer som, eller oppnevner styrer i klubbens heleide datterselskaper. c. Øvrige valg i henhold til årsmøte-vedtatt organisasjonsplan, jfr. § 15 pkt. 9. d. Kontrollkomité bestående av 3 medlemmer med 2 varamedlemmer. e. Representanter til ting og møter i de organisasjoner klubben er tilsluttet. f. Valgkomité med leder og 4 medlemmer og 1 varamedlem for neste årsmøte. -

UEFA EUROPA LEAGUE - 2019/20 SEASON MATCH PRESS KITS Stadionul Dr
UEFA EUROPA LEAGUE - 2019/20 SEASON MATCH PRESS KITS Stadionul Dr. Constantin Rădulescu - Cluj-Napoca Thursday 12 December 2019 CFR 1907 Cluj 18.55CET (19.55 local time) Celtic FC Group E - Matchday 6 Last updated 28/02/2020 19:26CET Previous meetings 2 Match background 3 Team facts 5 Squad list 7 Fixtures and results 10 Match-by-match lineups 13 Match officials 17 Legend 18 1 CFR 1907 Cluj - Celtic FC Thursday 12 December 2019 - 18.55CET (19.55 local time) Match press kit Stadionul Dr. Constantin Rădulescu, Cluj-Napoca Previous meetings Head to Head UEFA Europa League Date Stage Match Result Venue Goalscorers Édouard 20, 03/10/2019 GS Celtic FC - CFR 1907 Cluj 2-0 Glasgow Elyounoussi 59 UEFA Champions League Date Stage Match Result Venue Goalscorers Forrest 51, Édouard 3-4 61, Christie 76; Deac 13/08/2019 QR3 Celtic FC - CFR 1907 Cluj Glasgow agg: 4-5 27, Omrani 74 (P), 80, Ţucudean 90+7 Rondón 28; Forrest 07/08/2019 QR3 CFR 1907 Cluj - Celtic FC 1-1 Cluj-Napoca 37 Home Away Final Total Pld W D L Pld W D L Pld W D L Pld W D L GF GA CFR 1907 Cluj 1 0 1 0 2 1 0 1 0 0 0 0 3 1 1 1 5 6 Celtic FC 2 1 0 1 1 0 1 0 0 0 0 0 3 1 1 1 6 5 CFR 1907 Cluj - Record versus clubs from opponents' country CFR 1907 Cluj have not played against a club from their opponents' country Celtic FC - Record versus clubs from opponents' country UEFA Europa League Date Stage Match Result Venue Goalscorers William Amorim 79; 06/11/2014 GS FC Astra Giurgiu - Celtic FC 1-1 Giurgiu Johansen 32 Šćepović 73, 23/10/2014 GS Celtic FC - FC Astra Giurgiu 2-1 Glasgow Johansen 79; Enache 81 UEFA Cup Winners' Cup Date Stage Match Result Venue Goalscorers 1-0 01/10/1980 R1 FC Timişoara - Celtic FC Timisoara Paltinisan 81 agg: 2-2 ag Nicholas 18, 41; 17/09/1980 R1 Celtic FC - FC Timişoara 2-1 Glasgow Manea 77 Home Away Final Total Pld W D L Pld W D L Pld W D L Pld W D L GF GA CFR 1907 Cluj 1 0 1 0 2 1 0 1 0 0 0 0 3 1 1 1 5 6 Celtic FC 4 3 0 1 3 0 2 1 0 0 0 0 7 3 2 2 11 9 2 CFR 1907 Cluj - Celtic FC Thursday 12 December 2019 - 18.55CET (19.55 local time) Match press kit Stadionul Dr. -

Års Beretning 2011
ÅRSBERETNING 2011 ÅRS BERETNING 2011 Udgiver Dansk Boldspil-Union Fodboldens Hus DBU Allé 1 2605 Brøndby Telefon 4326 2222 Telefax 4326 2245 e-mail [email protected] www.dbu.dk Redaktion DBU Kommunikation Lars Berendt (ansvarshavende) Jacob Wadland Pia Schou Nielsen Mikkel Minor Petersen Layout/dtp DBU Grafisk Bettina Emcken Lise Fabricius Carl Herup Høgnesen Fotos Anders & Per Kjærbye/Fodboldbilleder.dk m.fl. Redaktion slut 16. februar 2012 Tryk og distribution Kailow Graphic Oplag 2.500 Pris Kr. 60,00 plus kr. 31,00 i forsendelse 320752_Omslag_2011.indd 1 14/02/12 15.10 ÅRSBERETNING 2011 ÅRS BERETNING 2011 Udgiver Dansk Boldspil-Union Fodboldens Hus DBU Allé 1 2605 Brøndby Telefon 4326 2222 Telefax 4326 2245 e-mail [email protected] www.dbu.dk Redaktion DBU Kommunikation Lars Berendt (ansvarshavende) Jacob Wadland Pia Schou Nielsen Mikkel Minor Petersen Layout/dtp DBU Grafisk Bettina Emcken Lise Fabricius Carl Herup Høgnesen Fotos Anders & Per Kjærbye/Fodboldbilleder.dk m.fl. Redaktion slut 16. februar 2012 Tryk og distribution Kailow Graphic Oplag 2.500 Pris Kr. 60,00 plus kr. 31,00 i forsendelse 320752_Omslag_2011.indd 1 14/02/12 15.10 Dansk Boldspil-Union Årsberetning 2011 Indhold Dansk Boldspil-Union U20-landsholdet . 56 Dansk Boldspil-Union 2011 . 4 U19-landsholdet . 57 UEFA U21 EM 2011 Danmark . 8 U18-landsholdet . 58 Nationale relationer . 10 U17-landsholdet . 60 Internationale relationer . 12 U16-landsholdet . 62 Medlemstal . 14 Old Boys-landsholdet . 63 Organisationsplan 2011 . 16 Kvindelandsholdet . 64 Administrationen . 18 U23-kvindelandsholdet . 66 Bestyrelsen og forretningsudvalget . 19 U19-kvindelandsholdet . 67 Udvalg . 20 U17-pigelandsholdet . 68 Repræsentantskabet . 22 U16-pigelandsholdet . -

Premier League: the Championship: Revansjejakt I Hovedstaden Ny Spenning I Tet Side 10 Side 14 INNHOLD Tipsuken
ÅRGANG 73 // TIRSDAG 23. JUNI 2020 // NR. 25 LØSSALG KR 80,– SIDE 3-7 SIDE ALARMENUsle ett poeng fra første to runder fikk alarmen til å dure i GÅRRosenborg-garderoben. Denne ukens møter med Glimt og Brann vil kunne definere trøndernes sesong. Premier League: The Championship: Revansjejakt i hovedstaden Ny spenning i tet Side 10 Side 14 INNHOLD Tipsuken .....................................................2 Norge Eliteserien .....................................3-7 Tipsbladet-duellen .....................................9 England Premier League .....................10-13 England The Championship ...............14-17 Liganytt .....................................................19 Tyskland Bundesliga ...........................20-22 Italia Serie A .........................................23-27 Spania La Liga ......................................28-33 Danmark Superligaen .........................34-36 Sverige Allsvenskan .............................38-40 Ukens TV-liste ......................................42-73 Tipsfondet............................................44-45 Midtukekupongen ....................................46 Lørdagskupongen ....................................47 Søndagskupongen ...................................48 Resultater.............................................49-63 Feriemodus Premier League-fotballen startet opp var Everton som kom nærmest med igjen forrige uke, men det ble på ingen en enorm dobbeltsjanse mot slutten. måte en eksplosjon av underholdning. At det etterlengtede ligagullet fortsatt Kanskje hadde -

2018 Topps Chrome Champions League Showcase Soccer
2018 Topps Chrome Champions Showcase Soccer 20 Teams; 16 Teams with Autographs AS Roma; Chelsea FC; FC Basal 1893; Sevilla FC - No Autographs Player Set Card # Team Fabinho Auto - Base 84 AS Monaco FC Jemerson Auto - Base 18 AS Monaco FC João Moutinho Auto - Base 26 AS Monaco FC Radamel Falcao Auto - Base 43 AS Monaco FC Radamel Falcao Auto - Lightning Strike LS-RF AS Monaco FC Fabinho Base 84 AS Monaco FC Jemerson Base 18 AS Monaco FC João Moutinho Base 26 AS Monaco FC Radamel Falcao Base 43 AS Monaco FC Thomas Lemar Base 4 AS Monaco FC Radamel Falcao Insert - Lightning Strike LS-RF AS Monaco FC GroupBreakChecklists.com 2018 Topps Chrome Champions Showcase Soccer Player Set Card # Team Daniele De Rossi Base 63 AS Roma Edin Džeko Base 86 AS Roma Kostas Manolas Base 96 AS Roma Radja Nainggolan Base 87 AS Roma Stephan el-Shaarawy Base 92 AS Roma GroupBreakChecklists.com 2018 Topps Chrome Champions Showcase Soccer Player Set Card # Team Marco Reus Auto - Base 35 Borussia Dortmund Mario Götze Auto - Base 67 Borussia Dortmund Christian Pulisic Base 25 Borussia Dortmund Marco Reus Base 35 Borussia Dortmund Mario Götze Base 67 Borussia Dortmund Pierre-Emerick Aubameyang Base 98 Borussia Dortmund Shinji Kagawa Base 27 Borussia Dortmund Christian Pulisic Base - Image Variation 25 Borussia Dortmund Christian Pulisic Insert - Future Stars FS-CP Borussia Dortmund Christian Pulisic Insert - Lightning Strike LS-CP Borussia Dortmund GroupBreakChecklists.com 2018 Topps Chrome Champions Showcase Soccer Player Set Card # Team Callum McGregor Auto - Base -

Wisla Kraków V Blackburn Rovers FC MATCH PRESS KIT Wisly, Krakow Thursday, 19 October 2006 - 16:45 Local Time Group E
Wisla Kraków v Blackburn Rovers FC MATCH PRESS KIT Wisly, Krakow Thursday, 19 October 2006 - 16:45 local time Group E Wisła Kraków will be hoping to make their European experience count as English side Blackburn Rovers FC head to Poland for the first match of their UEFA Cup Group E campaign. • The two teams have never met before in European competition. • Wisła boast a wealth of experience having made 74 appearances in European competition, winning 34, drawing 16 and losing 24. • However, they are yet to tackle English opposition in any of those matches and will be eager to make a positive start against Blackburn. • The Lancashire team have not enjoyed many happy times in European competition since making their first appearance in the 1994/95 UEFA Cup, going down to a 3-2 aggregate defeat by Trelleborgs IF of Sweden. • Of their 18 European games to date, Blackburn have won just two, drawing seven and losing nine. They beat Rosenborg BK 4-1 in the final game of their only UEFA Champions League group stage campaign in 1995/96, while a 2-0 win against FC Salzburg earned them the 4-2 aggregate win that put them through to this season's UEFA Cup group stage. • Blackburn secured their only previous success in a European tie on away goals against PFC CSKA Sofia in the 2002/03 UEFA Cup. • The Ewood Park side have met Polish opponents twice, taking on Wisła's arch-rivals Legia Warszawa twice in their ill-fated 1995/96 UEFA Champions League campaign. Polish international Jerzy Podbrozny scored the only goal in Warsaw in a 1-0 win for Legia before the sides drew 0-0 in the rematch in Blackburn.