Reference Curve for Indian Role Model Scientists
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
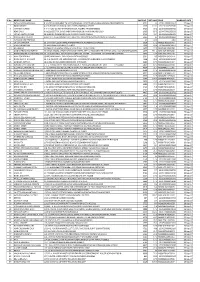
S.No BENEFICIARY NAME Address MICR NO NET AMOUNT FOLIO
S.No BENEFICIARY NAME Address MICR NO NET AMOUNTFOLIO WARRANT DATE 1 PATHA SATYANARAYANA # 1-5-262NEAR BHARAT TALKIESPADMASHALI STREETKARIMNAGAR ANDHRA PRADESH505001 5701 14 1205140000031510 29-Sep-17 2 RAM PARKASH # 64SUBHASH COLONYGALI NO. 01SIRSA HARYANA125055 1245 114.1 1201910102962980 29-Sep-17 3 J MAHESH KUMAR # 9 - 9 -120/ 1GIRIJIPETTAHWARANGAL ANDHRA PRADESH506002 5723 39.2 1202300000256760 29-Sep-17 4 RENU BALA #.No2914SECTOR 32-ACHANDIGARH ROADLUDHIANA PUNJAB141010 1965 87.5 1204470001565930 29-Sep-17 5 SHAMA SULTAN PIRANI #8-9-88,JPN ROADWARANGAL ANDHRA PRADESH506002 5722 43.4 1202300000286250 29-Sep-17 6 PHOOL SINGH VERMA (ELECT / FET)ELECTRICAL FLIGHT24 ED AIR FORCE MANAURIALLAHABAD U.P.212212 2365 35 1201320000168860 29-Sep-17 7 VENKATA RAO PRAYAGA . 27 53.2 2157 29-Sep-17 8 SATISH CHANDRA 01 SHIVPURI COLONYMAULANAGARNAINITAL ROADBAREILLY243122 2628 17.5 IN30267930518785 29-Sep-17 9 AJAY KUMAR DUBE 01 HARJI PHALYA,DHAR M.P.454001 5328 43.4 1203460000024910 29-Sep-17 10 MEENAKSHI 01/26Eastend ApartmentMayur Vihar, Phase- IDelhi110096 1407 17.5 IN30236510062768 29-Sep-17 11 MANOJ PRATAPRAI PAREKH 02 MILAN DHARA APPARTMENTAZAD STREET, OFF S V ROADANDHERI WESTMUMBAI, MAHARASHTRA400058 4836 351.4 IN30154918628486 29-Sep-17 12 BIPINCHANDRA GULABCHAND PAREKH03 ISHAVASHYAM SOCIETYNEAR NARAYAN NAGAR 1SHOPPING CENTRE,BHARUCH392001 4672 17.5 IN30133019451136 29-Sep-17 13 KAMLESH BENIWAL 03MEGHANANAVAL PARKVISAKHAPATNAM530005 5901 105 IN30232410431044 29-Sep-17 14 DINESHBHAI P. BHAVSAR 04-C- 6 SWAGAT APP. NRKARVNR SOC. AHMEDABADAHMEDABAD -

Current Affairs October 2019
LEGEND MAGAZINE (OCTOBER - 2019) Current Affairs and Quiz, English Vocabulary & Simplification Exclusively prepared for RACE students Issue: 23 | Page : 40 | Topic : Legend of OCTOBER | Price: Not for Sale OCTOBER CURRENT AFFAIRS the two cities from four hours to 45 minutes, once ➢ Prime Minister was speaking at a 'Swachh completed and will also decongest Delhi. Bharat Diwas' programme in Ahmedabad on ➢ As much as 8,346 crore is likely to be spent the 150th birth anniversary of Mahatma Gandhi. NATIONAL NEWS on the project, which was signed in March, 2016. ➢ Mr Modi said, the Centre plans to spend 3 lakh crore rupees on the ambitious "Jal Jivan PM addresses Arogya Manthan marking one Raksha Mantri Excellence Awards for Mission" aimed at water conservation. year of Ayushman Bharat; employees of Defence Accounts Department ➢ Prime Minister also released Launches a new mobile application for was given on its annual day. commemorative 150 rupees coins to mark the Ayushman Bharat ➢ Defence Accounts Department, one of the occasion ➢ Prime Minister Narendra Modi will preside over oldest Departments under Government of India, Nationwide “Paryatan Parv 2019” to the valedictory function of Arogya Manthan in is going to celebrate its annual day on October 1. promote tourism to be inaugurated in New New Delhi a two-day event organized by the ➢ Rajnath Singh will be Chief Guest at the Delhi National Health Authority to mark the completion celebrations, which will take place at Manekshaw ➢ The nationwide Paryatan Parv, 2019 to of one year of Ayushman Bharat, Pradhan Centre in Delhi Cantt. Shripad Naik will be the promote tourism to be inaugurated in New Delhi. -

PF Numberhrms No Name 508 8793271 B.G.GADGIL 519
PF NumberHrms No Name 508 8793271 B.G.GADGIL 519 8793336 W/O SRI.SYED DILAWAR ALI 520 8793344 W/O SRI.H.T.ELEDROOS 527 8793395 SRI N.SUDERSHAN 544 8793476 A.LAXMINARAYAN 547 8793492 N.PRABHAKAR SASTRY 552 8793530 MOHD ABDUL REHMAN 557 8793573 L H BHUNKAR 573 8793670 HUSSAIN KHAN 575 8793689 P.SOURIRAJAN 579 8793719 AMAR SINGH RAJPUT 584 8793751 SANT JOSHI 585 8793778 SYED CHAND 591 8793794 NANICHAND 592 8793808 L J ALASPURE 598 8793840 K.ISHWARIAH 599 8793859 J.SRINIVASULU 602 8793875 AMBUR HABIB 610 8793956 B CHENNAKISTAIAH 612 8793964 N S RAJU 613 8793972 T R KRISHNAMURTHY 614 8793980 ABDUL KHADER 617 8794006 K T KRISHNASWAMY 633 8794065 V P GIRI 636 8794103 M KASHINATH 637 8794111 M A RAHIM KHAN 643 8794162 G YELLAIAH 645 8794189 GULAM RASOOL 646 8794197 N RANGASWAMY 650 8794227 S VARADACHARY 658 8794316 D N JAGIRDAR 666 8794367 B.D.SHINDE 676 8794421 A.L.MUTHAIAH 689 8794502 SHEED 690 8794510 C V VITTAL 698 8794553 /O V H DEHPANDE 700 8794588 S SUBBAIAH 703 8794626 RAJAIAH 707 8794650 Y M LELE 709 8794677 T KRISHAN 714 8794723 AYACHIT 719 8794774 ORE 720 8794782 MANOHARLAL 721 8794790 R JOSHI 722 8794804 HANKER 727 8794812 AO 728 8794820 GANESHAN 731 8794847 HEED 732 8794855 ROOPNAR 737 8794901 ASOOL 740 8794944 RAMASWAMY 751 8795045 OMKAR SINGLI 753 8795061 SRI V.HANUMANTHA RAO 755 8795096 LATE K.SURYA PRAKASH RAO 756 8795118 S M R H KALEEMI 757 8795126 LATE SRI KARAM SINGH 759 8795142 NANDLALTEJU 760 8795150 LATE SRI M.JALAIAH 761 8795169 S S MAHA 762 8795177 Late Pandurang B Mane 764 8795193 Late Sri Hanumanthappa Ra 10014 8813981 T.ATCHUTA RAMA RAO 10093 8790779 G.G.AMINGAD 20059 8813795 K BHASKARAN 40070 8813876 RATHILAL BHULABAI DESAI 70067 8796289 B.K.GALGALI 110034 8813809 EKNATH P KULKARNI 110089 8813701 DIGAMBAR K RAO KULKARNI 110117 8814104 S.I. -

Igcnewsletter
ISSN 0972-5741 Volume 98 October 2013 IGCNewsletter IN THIS ISSUE Interaction with Eminent Personalities • Interaction with Dr. R. Chidambaram Technical Articles • Kinetics of Extraction of Ruthenium with Tri n-Butyl Phosphate/Dodecane • Effect of External Perturbation Induced Charge Order Melting of Pr0.5Ca0.5MnO3 on YBa2Cu3O7 Thin Film Young Officer’s Forum • Design and Development of Universal Signal Conditioning System for I&C of Future FBRs Young Researcher’s Forum • Development of Computational Intelligence Systems for Parameter Estimation and Event Identification in Fast Breeder Reactors News and Events • Graduation Function of the Seventh Batch of Trainee Scientific Officers of BARC Training School at IGCAR • Summer Training in Physics and Chemistry (STIPAC - 2013) • BITS Practice School Conference/Meeting Highlights • Quality Circle Annual Meet (QCAM) - 2013 Forthcoming Meeting/Conference • Recent Advances in Information Technology (READIT) Visit of Dignitaries Awards & Honours INDIRA GANDHI CENTRE FOR ATOMIC RESEARCH http://www.igcar.gov.in/lis/nl98/igc98.pdf IGC Newsletter From the Editor From the Editor Dear Reader It is my pleasant privilege to forward a copy of the latest issue of IGC Newsletter (Volume 98, October 2013 issue). In this issue we have had the privilege of Dr. R. Chidambaram, Principal Scientific Advisor to the Government of India, Chairman of the Scientific Advisory Committee to the Cabinet and former Chairman, Atomic Energy Commission, sharing his experiences with a team of young officers. In the first technical article Shri N.K. Pandey and colleagues have discussed the extraction kinetics of ruthenium with tri n-butyl phosphate/dodecane system. In the second technical article Shri Dipak Kumar Baisnab and colleagues have described the experimental studies of the effect of external perturbation such as substrate induced strain, applied current and magnetic field on Pr0.5Ca0.5MnO3 on YBa2Cu3O7 thin film heterostructures. -

A Thousand Suns: Political Motivations for Nuclear Weapons Testing
A Thousand Suns: Political Motivations for Nuclear Weapons Testing by Whitney Lyke Raas B.S., Physics (2001) University of California, Los Angeles Submitted to the Department of Political Science in Partial Fulfillment of the Requirements for the Degree of Masters of Science in Political Science at the Massachusetts Institute of Technology September 2006 C 2006 Massachusetts Institute of Technology All rights reserved Signature of Author Department of Political Science August 14, 2006 Certified by , M"A '."'r-,. t , %ff S- HirveySap 4sky Professor of Political Science, Emeritus Thesis Advisor Accepted by Roger Petersen MASSACHUSETTS INST•UTE. Associate Professor of Political Science OF TECHNOLOGY Chairman, Graduate Program Committee SEP 2 12006 ARCHIVES LIBRARIES A Thousand Suns: Political Motivations for Nuclear Weapons Testing by Whitney Lyke Raas Submitted to the Department of Political Science on August 14, 2006 in Partial Fulfillment of the Requirements for the Degree of Masters of Science in Political Science ABSTRACT Nuclear weapon testing is the final step in the nuclear development process, an announcement of ability and strength. The consequences of a nuclear test are far from easy to bear, however: economic sanctions can be crippling and nuclear capability automatically makes one a nuclear target. Why, then, do states test nuclear weapons? This thesis aims to determine the answer to this question using India as a model. It is well known that India tested nuclear weapons in 1974 and in 1998, but less well known are the near-tests of 1983, 1995, and 1996. This thesis examines the situation in these years and the details of the nuclear decisions based on four hypotheses: technical concerns, security and power, domestic politics, and norms and ideas. -

Report Idea 1
Science Policy and Security AAAS activities are helping to promote the responsible use of science and technology to improve human well-being. From testimony on technologies for detecting “dirty bomb” components, to a highly regarded fellowship program and gold-standard R&D budget analysis, AAAS seeks to provide objective, authoritative scientific and technological insights to policy-makers. In 2005, AAAS science policy efforts focused on improving innovation, promoting international collaboration, enhancing national security, and more. Innovation and Competitiveness in the United States AAAS urged the President and Congress to take strong steps to sustain American innovation by investing in high-risk, breakthrough research and by improving science education at all levels. “We do not want to put our country and our knowledge-based, technology-driven economy in the position of ‘catch-up,’” wrote Gilbert S. Omenn of the University of Michigan, Ann Arbor, then AAAS President, in a 9 December letter to U.S. President George W. Bush. Meanwhile, AAAS Chairman of the Board Shirley Ann Jackson contributed to the National Academies’ report, Rising Above the Gathering Storm, and worked with the Council on Competitiveness Innovation Initiative. Those efforts culminated with the National Summit on Competitiveness, hosted by the U.S. Department of Commerce in conjunction with other Cabinet-level departments and business organizations. As president of Rensselaer Polytechnic Institute, Jackson also wrote to President Bush, warning that “our science and technology position is a looming national crisis because it robs us of our capacity for innovation.” President Bush subsequently released his American Competitiveness Initiative, which proposes broad investment in research and development, education, entrepreneurship, and innovation. -

Winners of Awards and Medals, and Memorial Lecturers Iim Honors
WINNERS OF AWARDS AND MEDALS, AND MEMORIAL LECTURERS IIM HONORS HONORARY MEMBERS Purpose Eligibility For distinguished services to IIM Membership is not mandatory the Metallurgical Industry, / No posthumous selection. Research, Education & to The (Total number of Living Honorary Indian Institute of Metals Members not to exceed 100) Out of the HONORARY MEMBERS elected so far, 42 are deceased. Living: 75 1 1949 Late Jehangir J. Ghandy 76 2003 Late P Ramachandra Rao 2 1952 Late G.C. Mitter 77 2004 Dr. S. K. Bhattacharyya 3 1954 Late P.H. Kutar 78 2004 Prof. Subra Suresh 4 1956 Late K.S. Krishnan 79 2005 Dr T K Mukherjee 5 1958 Late M.S. Thacker 80 2005 Prof Hem Shanker Ray 6 1960 Late G.K. Ogale 81 2005 Late K P Abraham 7 1961 Late S.K. Nanavati 82 2005 Dr Sanak Mishra 8 1963 Late K.H. Morley 83 2006 Dr. Baldev Raj 9 1965 Late Dara P. Antia 84 2006 Prof. Akihisa Inoue 10 1966 Late Morris Cohen 85 2006 Dr. C. K. Gupta 11 1967 Late B.R. Nijhawan 86 2006 Dr. R. A. Mashelkar 12 1972 Late J.R.D. Tata 87 2006 Late V R Subramanian 13 1973 Late Brahm Prakash 88 2007 Shri B. Muthuraman 14 1973 Late C.S. Smith 89 2007 Prof. Thaddeus B. Massalski 15 1973 Late B. Chalmers 90 2007 Prof. Subhash Mahajan 16 1974 Late Dr. M.N. Dastur 91 2007 Dr. Rajagopala Chidambaram 17 1975 Late P. Anant 92 2007 Shri Baba N. Kalyani 18 1976 Late F.A.A. -
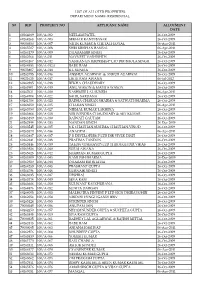
S# Rid Property No Applicant Name Allotment Date 1
LIST OF ALLOTED PROPERTIES DEPARTMENT NAME- RESIDENTIAL S# RID PROPERTY NO APPLICANT NAME ALLOTMENT DATE 1 60264689 100/A-002 NEELAM PATEL 26-Oct-2009 2 60264268 100/A-003 SEKHAR KANTI BASAK 26-Oct-2009 3 90000350 100/A-007 NITIN KUMAR & CHETALI GOYAL 06-Apr-2011 4 60265507 100/A-008 SHRI KRISHAN BANSAL 06-Apr-2011 5 60264179 100/A-009 DHARAMBIR SINGH 26-Oct-2009 6 60262564 100/A-011 NAVNEET VASHISHTH 26-Oct-2009 7 60264167 100/A-012 YASIKAN ENTERPRISES P LTD DIR BHOLA SINGH 26-Oct-2009 8 60264553 100/A-012A BABU RAM 26-Oct-2009 9 90023807 100/A-014 K L SUNEJA 26-Oct-2009 10 60265795 100/A-016 ANSHUL AGARWAL & ANKUR AGARWAL 26-Oct-2009 11 90021623 100/A-017 LIKHI RAM AWANA 06-Jul-2012 12 60262985 100/A-018 REKHA CHAUDHARY 26-Oct-2009 13 60263901 100/A-019 ANIL WASON & MAMTA WASON 26-Oct-2009 14 60267621 100/A-020 KASHMIRI LAL SUNEJA 06-Apr-2011 15 60264704 100/A-022 SAHIL SARDANA 26-Oct-2009 16 60261786 100/A-023 RADHA CHARAN SHARMA & SATWATI SHARMA 26-Oct-2009 17 60266050 100/A-025 CHARAN SINGH 06-Apr-2011 18 60263750 100/A-027 NIRMAL KUMAR LAKHINA 26-Oct-2009 19 60263868 100/A-028 VISHVENDRA CHAUDHARY & AJIT KUMAR 26-Oct-2009 20 60263189 100/A-030 RAJWATI GAUTAM 26-Oct-2009 21 60262994 100/A-033 NANDAN SINGH 26-Dec-2009 22 60263545 100/A-035 S K CHAUHAN,SUSHMA CHAUHAN,VINOD 26-Oct-2009 23 60265570 100/A-036 ANAGPAL 06-Apr-2011 24 60262887 100/A-037 P R DEVELOPERS P LTD DIR VIVEK DIXIT 26-Oct-2009 25 60262241 100/A-038 PRATIMA TANDON 26-Oct-2009 26 60263846 100/A-039 TALON VINIMAY(P) LTD THROUGH DIR.VIKAS 26-Oct-2009 27 60263926 100/A-040 -

Abstracts-Book-Final
Sci-Fi Group By Indian Association for Science Fiction Studies (IASFS) 1 INDEX Sr. Page Name Title No. no. 1. Editorial Board - 6 2. From chief editor’s desk - 7 DLKIA: A Deep Neural Network Based Gerard Deepak, Pushpa C N, Knowledge Integration Approach for 3. Ayush Kumar, Thriveni J, 8 Knowledge Base Generation for Science Venugopal K R Fiction as a Domain Androids, Surveillance and Evil: An 4. Dr Kasturi Sinha Ray 9 Overview of Jonathan Nolan’s Westworld Racial Discrimination and Scientific Priyadharshini Krishnan & 5. Amelioration in Isaac Asimov’s 10 Akshaya Subramaniam ‘The Weapon too dreadful to use’ A Post humanist Reading of Homo Deus: A 6. Shikha Khandpur 11 Brief History of Tomorrow S. Priya Dharshini, Dr C. G. Frankenfood: A Cornucopia in Paolo 7. 12 Sangeetha Bacigalupi’s The Windup Girl Abnormal Human Beings in Hindu 8. Dr Shantala K R 13 Mythology and Possible Medical Explanation Bangalore’s Urban Ecology Crises: Science 9. Dr Sindhu Janardan 14 Fiction to the Rescue? Dystopian Awakening: Ecocritical 10. Dr Swasti Sharma Rumination on Climate Change in Narlikar’s 15 “Ice Age Cometh” Science Fiction, Women and Nature: 11. Mr. Kailash ankushrao atkare 16 Ecological Perspective Cyrano de Bergerac: Father of Science- 12. Dr Jyothi Venktaesh 17 Fiction Literature in France? A Reflection Kavin Molhy P. S, Dr C. G. Delineation of Optimistic Women in The 13. 18 Sangeetha Calculating Stars Breaking the Myth: Women as Superheroines 14. Nabanita Deka 19 and Supervillains in a Dystopian World Female Characters in Science Fiction: 15. Dr Navle Balaji Anandrao Archetypal Messengers of Social Equity and 20 Equality Exploring the Gamut of African American 16. -

The Newspaper of SRMIST
The Newspaper of SRMIST For private circulation only Volume 13 Number 1 The Founder Chancellor flanked by the Vice Chancellor (left) and Pro Vice Chancellor (Right) on the announcement of 300 Scholarships The Founder Chancellor Presenting a memento to Mr.N.Gopalaswami, former Chief Election Commissioner 2 2019 | Spectrum | Volume 13 Number 1 Photo taken during “Train the Trainer” program “Train the Trainer” STAFF WRITER 1 To train the students/faculty Management team of EY in selected Mr E.V. Abhishek Anand the intern etc., where around l30 on the subject by name the areas of US Taxation for a final year MBA student of lnterns-from various colleges With the expanding role of “International Taxation and Individuals, US Taxation for SRM School of Management, all around India including business globally, Faculty of Technology” Partnership firms, US Taxation SRM Institute of Science and leading B Schools like IIMs Management, SRM Institute of for Corporate and Transfer Technology, Kattankulathur 2 To hire the students for Summer took part in the race, and where Pricing during the academic as a “SELECT INTERN” for Science and Technology (formerly Internship with a stipend of E.V. Abhishek Anand got the year 2018-19 for a period of the fiscal year 2019 to attend known as SRM University) ` 20,000 per month opportunity and brought laurels provides a platform for the 10 days in their EY office at the EY’s annual International to SRM School of Management, students and the companies by 3 To hire the students for Bengaluru. Leadership Conference along SRM Institute of Science and permanent role in EY Global with 9 other interns from India signing mutually beneficial MoUs Also 8 out of 18 final year Technology, Kattankulathur. -

1 Minutes of the Meeting of the Executive Council Held on Saturday
1 MINUTES OF THE MEETING OF THE EXECUTIVE COUNCIL HELD ON SATURDAY, THE 3rd NOVEMBER, 2012 AT 2.00 P.M. IN THE COUNCIL ROOM, UNIVERSITY OF DELHI DELHI-110007 No. 5 PRESENT 1. Prof. Dinesh Singh Vice-Chancellor - Chairman 2. Prof. Vivek Suneja Pro-Vice-Chancellor 3. Prof. Sudhish Pachauri Dean of Colleges 4. Prof. Umesh Rai Director, UDSC 5. Dr. Savita M. Dutta Director, C.O.L. 6. Prof. Satwanti Kapoor Proctor 7. Mr. Anurag Shokeen 8. Dr. Deepak Malhotra 9. Mr. Javid Chowdhury 10. Prof. Prabhjot S. Kulkarni 11. Dr. K.S. Bhati 12. Mr. Rajib Ray 13. Prof. S.C. Bhatla 14. Dr. Satender Kumar Joshi 15. Dr. Shiba C. Panda 16. Mr. V.K. Misra 17. Prof. Upreet Dhaliwal SPECIAL INVITEES 1. Prof. Ajay Kumar 2. Prof. J.M. Khurana 3. Prof. Kamala Sankaran 2 4. Sh. R.N. Vashistha 5. Sh. Sanjay Jha 6. Mr. Z.V.S. Prasad Ms. Alka Sharma, Registrar - Secretary WELCOME 34/ At the outset, the Council welcomed the following who had become member of the Executive Council: 1. Prof. Satish Deshpande, Dean, Faculty of Social Sciences 2. Prof. Upreet Dhaliwal , Dean, Faculty Homoeopathy 3. Sh. Vinod Kumar Misra, Visitor’s Nominee 4. Sh. Naveen Chawla, Visitor’s Nominee 5. Sh. Z.V.S. Prasad, Special Invitee APPRECIATION 35/ The Council placed on record its deep sense of gratitude and appreciation for the services rendered by the following during their tenure as member of the Executive Council: 1. Prof. I. Usha Rao, Proctor 2. Prof. H.S. Prasad, Dean, Faculty of Arts 3. -

Neuf Au Rcpl Et Six Au
MAZAVAROO | N°28 | SAMEDI 8 FÉVRIER 2020 mazavaroo.mu RS 5.00 PAGES 4-5 Raj Pentiah : "Je regrette d'avoir cru dans le volume de mensonges de navin ramgoolam" SMP.MU 14 N°28 - SAMEDI 08 FEVRIER 2020 PAGES 6-7 Pages 18-19 Discours-Programme Neuf au RCpl et six au RCc MarieLes "YoungClaire Phokeerdoss Shots" Les Royalistes accaparent 1/3 de la RENCONTREcuvée de 2019 du MSM volent Marie Claire Phokeerdoss:la vedette « La SMP vient en aide aux démunis de Beau-Vallon » arie Claire Phokeerdoss est âgée de 73 ans. Elle a sous sa responsabilité deux petits-enfants et dépend uniquement de sa pension de vieillesse pour les nourrir. Marie Claire raconte qu’elle pu mo okip 2 zenfants, lavi trop Ms’occupe des enfants de sa fille chere, » affirme-t-elle. depuis qu’ils sont nés. « Zot ti Afin d’aider Marie Claire à encore tibaba ler zot inn vinn ress joindre les deux bouts, la SMP a avek moi. Ena fois zot mama vinn offert des fournitures scolaires à guet zot, » dit-elle avec tristesse. ses petits-enfants. « Ban zenfan la La septuagénaire ne baisse jamais inn gagne ban materiaux scolaires. PAGE 3 les bras. Avec le soutien des autres Zot inn gagne sak, soulier lekol, membres de sa famille, Marie cahier ek ban lezot zafer lekol, Claire essaie tant bien que mal » dit-elle avec satisfaction. « Sa editorial de subvenir aux besoins de ses fer moi enn gran plaisir ki ban deux petits-enfants, âgés de 5 association cuma SMP pe vinn et 11 ans.